إثبات علاقات بين الزوايا - الرياضيات 1-1 - أول ثانوي
الفصل1: التبرير والبرهان
الفصل2: التوازي والتعامد
نشاط الفصل 1: التبرير والبرهان
نشاط الفصل 2: التوازي والتعامد
رابط الدرس www.ien.edu.sa إثبات علاقات بين الزوايا Proving Angles Relationships 1-8 فيما سبق: درست تعيين أزواج خاصة من الزوايا واستعملتها (مهارة سابقة ) والآن : أكتب براهين تتضمن زوايا متتامة وزوايا متكاملة. أكتب براهين تتضمن زوايا متطابقة وزوايا قائمة. لماذا؟ تلاحظ أن 1 بين شفرتي المقص ، و 2 بين الشفرة ومقبض المقص تشكلان زوجًا من الزوايا المتجاورة على مستقيم. وبالمثل فإن 2 و 3 بين مقبضي المقص تشكلان أيضا زوجًا من الزوايا المتجاورة على مستقيم. 2 3 الزوايا المتتامة والمتكاملة توضّح مسلّمة المنقلة العلاقة بين قياس الزوايا والأعداد الحقيقية. أضف إلى مطويتك مسلمة 1.10 مسلمة المنقلة التعبير اللفظي تستعمل المنقلة للربط بين قياس زاوية وعدد حقيقي يقع بين °0 و °180. مثال: في ABC ، إذا انطبق صفر المنقلة على BA ، فإن العدد الذي ينطبق على BC يمثل قياس LABC. 100 110 80 90 120 80 70 130 70 60 100 50 140 E-- 30 =- 40 50 ☐ 150 140 130 -8-6- 60 I 120 110 A أضف إلى مطويتك J وزارة التعليم Ministry of Education 2024-1446 B درست سابقا مسلّمة جمع أطوال القطع المستقيمة، وتوجد علاقة مشابهة لها بين قياسات الزوايا. B (x+y) A K له 2 1 L 2 3. A B y° D C مسلمة 1.11 مسلمة جمع قياسات الزوايا تقع النقطة D داخل ABC إذا وفقط إذا كان mZABD+mZDBC=mZABC مثال 1 استعمال مسلمة جمع قياسات الزوايا إذا كان °145 = m2 = 56, mJKL فأوجد m1. برّر خطوات حلّك. مسلمة جمع قياسات الزوايا عوض °145 = m22 = 56°, mLJKL اطرح 56 من الطرفين بسط mZ1 + mZ2 = mZJKL mZ1 + 56° = 145° mZ156° 56° = 145° – 56° mZ1 = 89° تحقق من فهمك 1) إذا كان °131 = m1 = 23°, m ZABC، فأوجد m3. برر خطوات حلّك. الفصل 1 التبرير والبرهان 66

مراجعة المفردات يمكن استعمال مسلّمة جمع قياسات الزوايا مع علاقات أخرى على الزوايا؛ لإثبات نظريات تتعلق بالزوايا. الزوايتان المتكاملتان نظريتان أضف إلى مطويتك 1.3 نظرية الزاويتين المتكاملتين : إذا كانت الزاويتان متجاورتين على مستقيم، فإنهما متكاملتان. هما زاويتان مجموع قياسيهما يساوي °180 الزوايتان المتتامتان هما زاويتان مجموع قياسيهما يساوي 90 الزاويتان المتجاورتان على مستقيم هما زاويتان متجاورتان بحيث يكون ضلعاهما غير المشتركين نصفي مستقيم متعاكسين مثال: 12 متجاورتان على مستقيم، إذن °180 = mZ1 + mZ2 1.4 نظرية الزاويتين المتتامتين: إذا شكل الضلعان غير المشتركين لزاويتين متجاورتين زاوية قائمة، فإن الزاويتين تكونان متتامتين. 2 2 1 مثال ضلعا الزاويتين المتجاورتين 12 غير المشتركين يشكلان زاوية قائمةً، إذن °90 = m21 + mZ2 سوف تبرهن النظريتين 1.3 و 1.4 في السؤالين 14 و 15 مثال 2 من واقع الحياة استعمال خصائص الزوايا المتكاملة أو المتتامة مسح الأراضي: قام مساح بقياس الزاوية بين خط نظره إلى قمة تلة والمستقيم الرأسي فكانت °73 تقريبًا. ما قياس الزاوية بين خط نظره والخط الأفقي؟ برّر خطوات الحل. افهم ارسم شكلا يوضح المسألة. قاس المسّاح الزاوية بين خط نظره والخط الرأسي؛ لذا ارسم نصف المستقيم الرأسي والأفقي من النقطة التي يشاهد منها المساح التلة، ثم سمّ الزوايا الناتجة. وكما تعلم فإن نصفي المستقيمين الأفقي والرأسي) يكونان زاويةً قائمةً. 6 7 2 -> خطط: استعمل نظرية الزاويتين المتتامتين. حل بما أن 1 و 2 تكوّنان زاوية قائمة فإنهما متتامتان. نظرية الزاويتين المتتامتين m1 = 73° mZ1 + mZ2 = 90° 73° + mZ2 = 90° 73° +mZ2 - 73° = 90° - 73° اطرح 73 من الطرفين بسط mZ2 = 17° قياس الزاوية بين خط نظر المساح وخط الأفق °17 تحقق تعلم أنه يجب أن يكون ناتج جمع قياسي 21 و 22 يساوي °90 ✓ 17° 73° = 90° تحقق من فهمك (2) في الشكل المجاور ، 6 و 7 متجاورتان على مستقيم. إذا كان: °(32 + m26 = (3x و °12 + m27 = (5x ، 6 فأوجد قيمة 7, x, m6. برّر خطوات الحل. 18 الدرس - إثبات علاقات بين الزوايا الت P67 Ministry of Education 2024-1446

الزاويتان المتكاملتان والزاويتان المتتامتان
68 الفصل 1 التبرير والبرهان تطابق الزوايا: إن الخصائص الجبرية التي تنطبق على تطابق القطع المستقيمة وتساوي قياساتها، تنطبق أيضًا على تطابق الزوايا وتساوي قياساتها. نظرية 1.5 خصائص تطابق الزوايا خاصية الانعكاس للتطابق Z1 Z1 خاصية التماثل للتطابق إذا كانت 22 = 21 ، فإن 1 = 22. خاصية التعدي للتطابق 2 3 أضف إلى مطويتك 1 إذا كانت 22 = 1 ، وكانت 23 = 22، فإن 23 = 21. ستُبرهن خاصيتي الانعكاس والتعدي للتطابق في السؤالين 16 و 17 برهان المعطيات: LA LB المطلوب : BELA خاصية التماثل للتطابق A أضف إلى مطويتك برهان حر B تعلم من المعطيات أن A B . ومن تعريف تطابق الزوايا يكون MA = MB، وباستعمال خاصية التماثل للمساواة يكون MLB = mLA، وعليه فإن BIEN LA من تعريف تطابق الزوايا. يمكنك تطبيق الخصائص الجبرية لإثبات نظريات على تطابق الزوايا تتضمن زوايا متتامة وزوايا متكاملة. نظريتان 1.6 نظرية تطابق المكملات الزاويتان المكملتان للزاوية نفسها أو لزاويتين متطابقتين تكونان متطابقتين. مثال : إذا كان °180 = mZ1 + mZ2، وكان °180 = mZ2 + mZ3 ، فإن 23 = 1 1.7 نظرية تطابق المتممات الزاويتان المتممتان للزاوية نفسها أو لزاويتين متطابقتين تكونان متطابقتين. مثال : إذا كان °90 = mZ4 + mZ5 و °90 = m25 + m26 ، فإن 26 = 4 ستُبرهن حالة من النظرية 1.7 في السؤال 4 3 5 6 أضف إلى مطويتك الله وزارة التعليم Ministry of Education 2024-1446

مراجعة المفردات الزاويتان المتقابلتان بالرأس برهان المعطيات: 1 و 3 متكاملتان. 2 و 3 متكاملتان. المطلوب : 2 = 1 البرهان : العبارات 1) 21 و 23 متكاملتان. 2 و 3 متكاملتان. أضف إلى إحدى حالات نظرية تطابق المكملات مطويتك mZ1 + mZ3 = 180°, mZ2 + mZ3 = 180° (2 mZ1 + mZ3 = mZ2 + mZ3 (3 mZ1=mZ2 (4 21 = 22 (5 3 له 1) معطيات المبررات (2 تعريف الزاويتين المتكاملتين (3) بالتعويض 4) خاصية الطرح للمساواة (5) تعريف تطابق الزوايا مثال 3 براهين تستعمل فيها نظريتا تطابق المكملات أو المتممات أثبت أن الزاويتين المتقابلتين بالرأس 2 و 4 في الشكل المجاور متطابقتان. المعطيات 2 و 4 متقابلتان بالرأس. المطلوب : 24 = 22 2 4 3 هما زاويتان غير متجاورتين تتكونان من تقاطع مستقيمين. البرهان العبارات 1) 2 و 4 متقابلتان بالرأس. 2 22 و 23 متجاورتان على مستقيم. 3 و 4 متجاورتان على مستقيم. (3) 22 و 23 متكاملتان. 3 و 4 متكاملتان. Z24 (4 1) معطيات المبررات (2) تعريف الزاويتين المتجاورتين على مستقيم (3) نظرية الزاويتين المتكاملتين (4) نظرية تطابق المكملات تحقق من فهمك (3) في الشكل المجاور ABE و DBC قائمتان. أثبت أن ABD = EBC. D E B C A المثال ،3 ، لاحظ أن 2 و 4 متقابلتان بالرأس. ونتيجة هذا المثال تُثبت نظرية الزوايا المتقابلة بالرأس الآتية: نظرية 1.8 نظرية الزاويتين المتقابلتين بالرأس أضف إلى مطويتك الزاويتان المتقابلتان بالرأس متطابقتان. مثال: 21 = 23 22 = 24 2 3 4 الدرس 8- إثبات علاقات بين الزوايا الت P69 Ministry of Education 2024-1446

الزاويتان المتقابلتان بالرأس
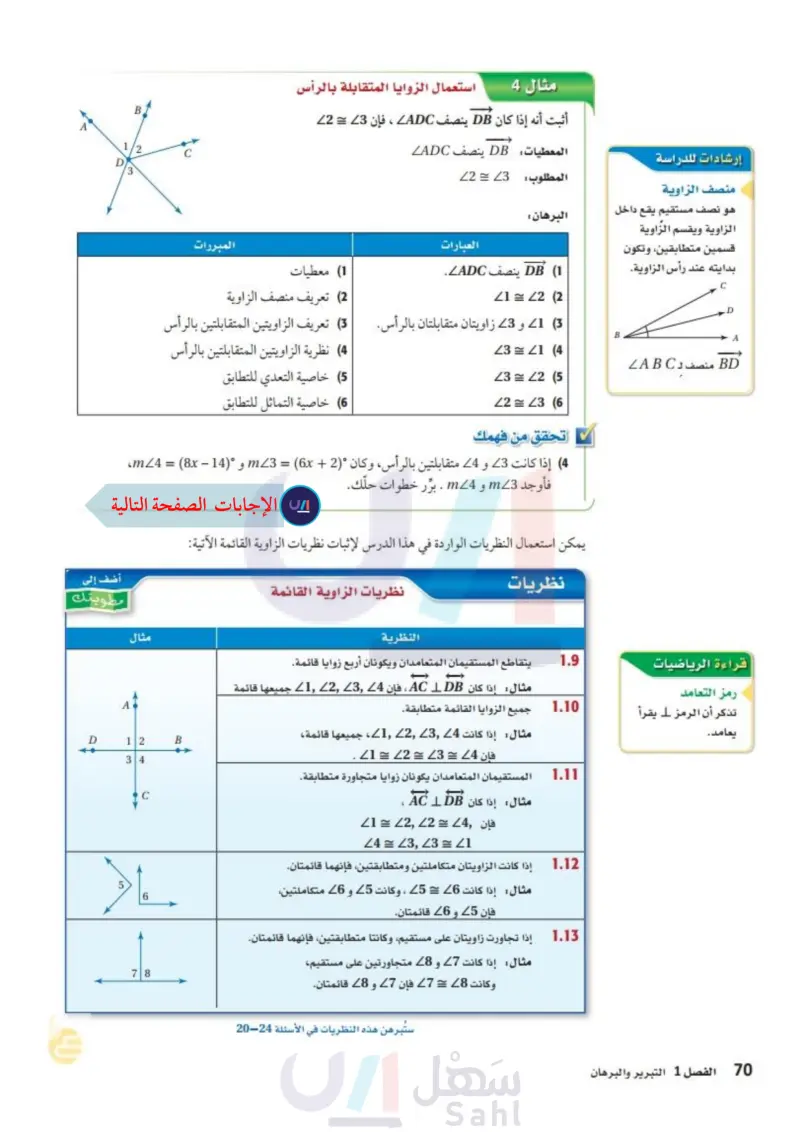
مثال 4 استعمال الزوايا المتقابلة بالرأس إرشادات للدراسة منصف الزاوية هو نصف مستقيم يقع داخل الزاوية ويقسم الزاوية قسمين متطابقين، وتكون بدايته عند رأس الزاوية أثبت أنه إذا كان DB ينصف ADC ، فإن 23 = 2 المعطيات: DB ينصف ADC المطلوب : البرهان 22 = 23 العبارات 1 DB ينصف LADC. 1) معطيات A D C BD منصف د LABC قراءة الرياضيات رمز التعامد تذكر أن الرمز 1 يقرأ يعامد. 70 المبررات B 1/2 C D 3 21 = 22 (2) (2) تعريف منصف الزاوية (3) 1 و 3 زاويتان متقابلتان بالرأس. (3) تعريف الزاويتين المتقابلتين بالرأس B 3 = 21 (4) 23 = 22 (5) 22 = 23 (6 (4) نظرية الزاويتين المتقابلتين بالرأس (5) خاصية التعدي للتطابق (6) خاصية التماثل للتطابق الفصل 1 التبرير والبرهان تحقق من فهمك (4) إذا كانت 3 و 4 متقابلتين بالرأس، وكان 2 + m 3 = 6x و °14 - m 24 = (8x، فأوجد 3 m و m4 . برّر خطوات حلّك . يمكن استعمال النظريات الواردة في هذا الدرس لإثبات نظريات الزاوية القائمة الآتية: 1.9 نظريات 1.10 1.11 1.12 1.13 نظريات الزاوية القائمة النظرية -> -> يتقاطع المستقيمان المتعامدان ويكونان أربع زوايا قائمة. مثال إذا كان AC 1 DB ، فإن 13 جميعها قائمة , جميع الزوايا القائمة متطابقة. مثال: إذا كانت 4 ,3 ,2 ,1، جميعها قائمة، فإن 14 = 2 = 22 = 21 المستقيمان المتعامدان يكونان زوايا متجاورة متطابقة. مثال : إذا كان AC IDB ' فإن 24 ,2 = 21 Z4 Z3, Z3 ≈ 21 إذا كانت الزاويتان متكاملتين ومتطابقتين، فإنهما قائمتان. مثال: إذا كانت 26 25 ، وكانت 5 و 6 متكاملتين، فإن 25 و 26 قائمتان. إذا تجاورت زاويتان على مستقيم، وكانتا متطابقتين، فإنهما قائمتان. مثال إذا كانت 7 و 8 متجاورتين على مستقيم، وكانت 28 27 فإن 27 و 28 قائمتان. ستُبرهن هذه النظريات في الأسئلة 24-20 مثال A أضف إلى A مطويتك D 12 34 B C > 6 78 وزارة التعليم Ministry of Education 2024-1446

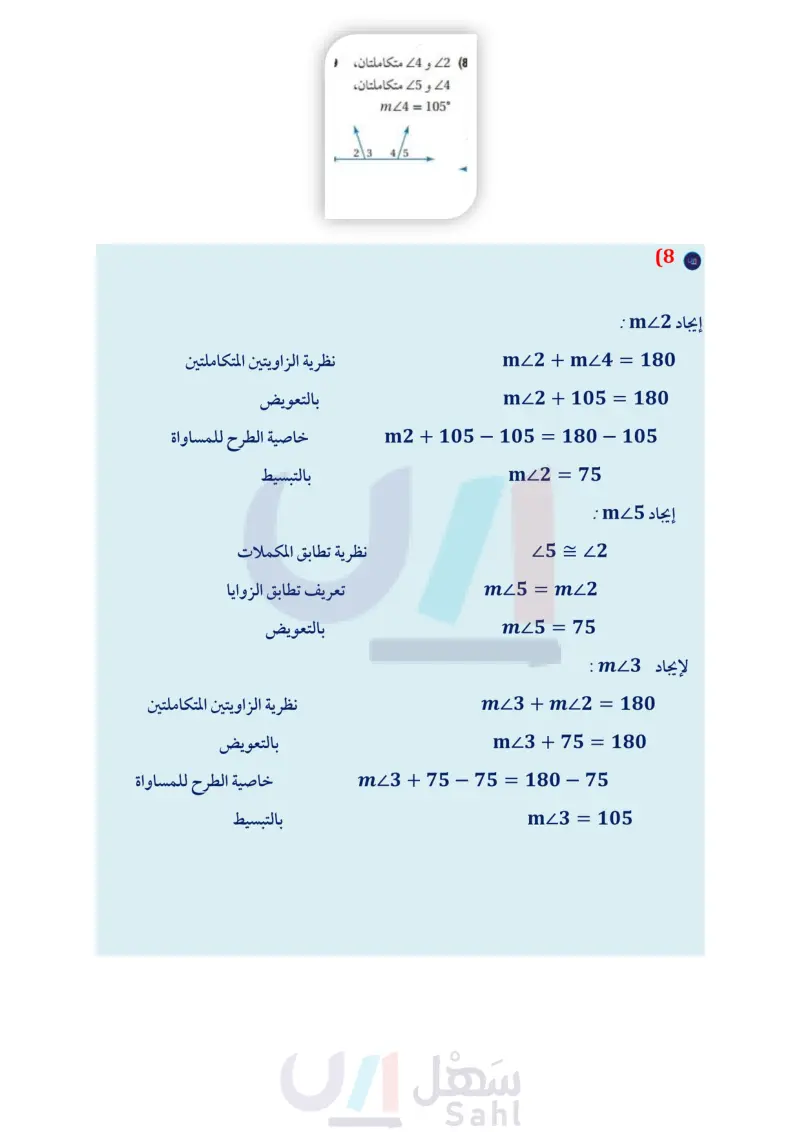
رمز التعامد
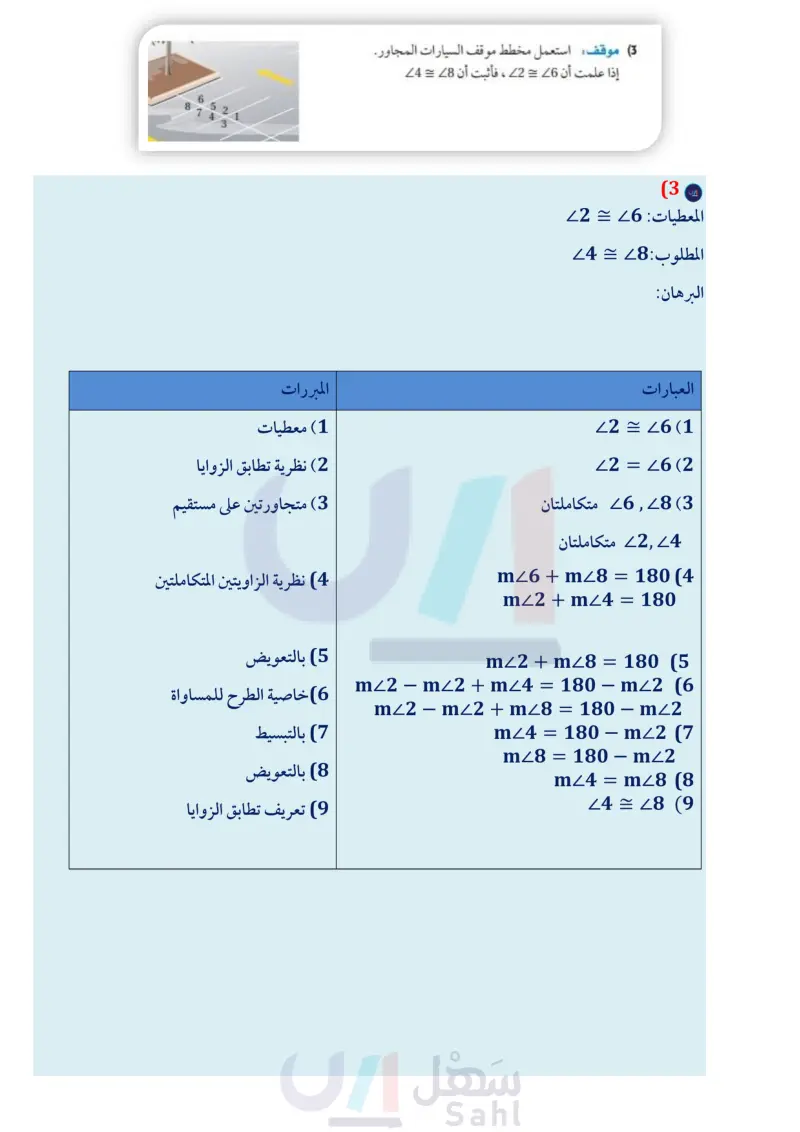
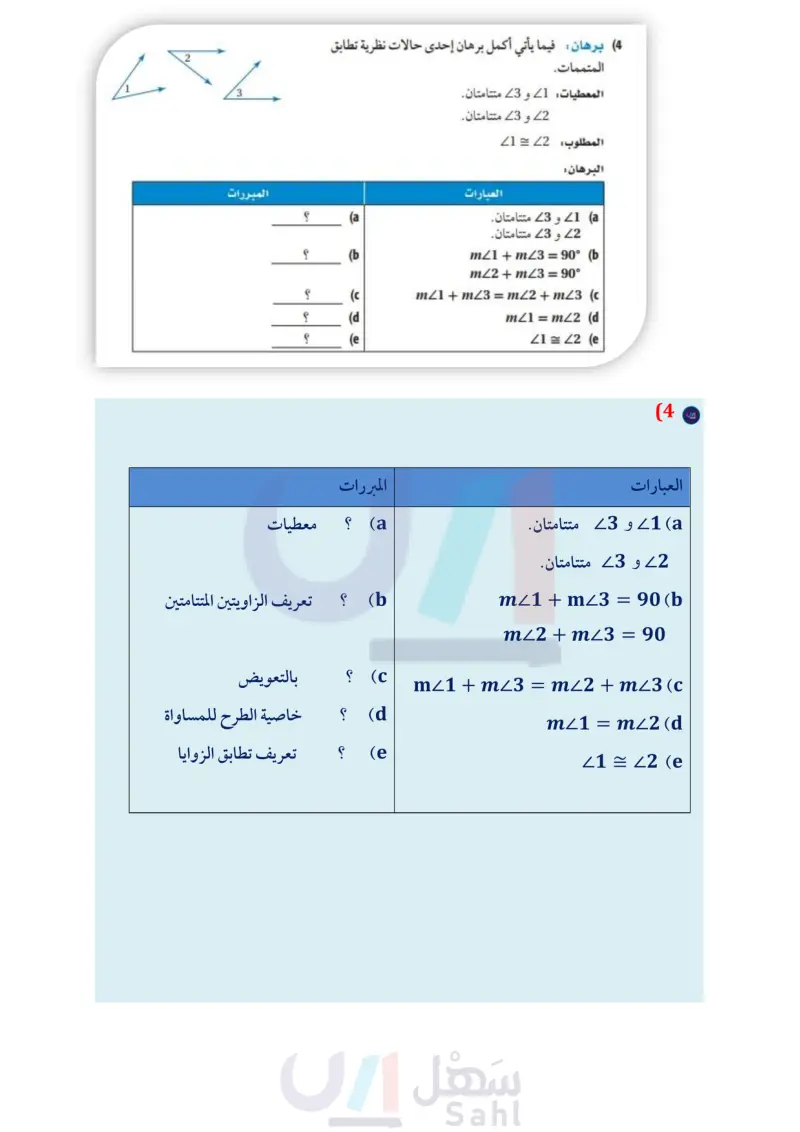
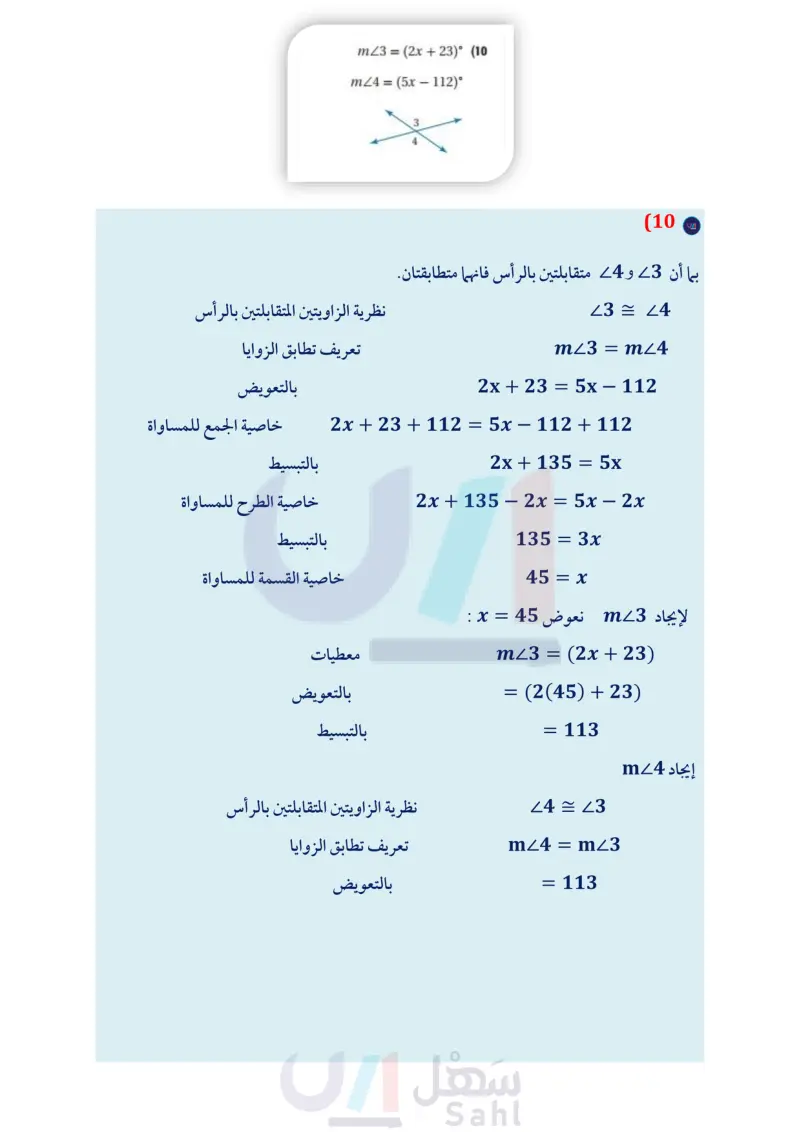
أوجد قياس الزوايا المرقمة في كل مما يأتي، واذكر النظريات التي تبرر حلك. المثال 1 m24 (3(x-1))°, m25 = (x + 7)° (2 = (x+7)° 6 7 52 4 3 ८९% 3 54 mZ2 = x°, m Z3 = (x−16)° (1 3 (3) موقف: استعمل مخطط موقف السيارات المجاور. المثال 2 إذا علمت أن 26 ، فأثبت أن 28 = 4 (4) برهان فيما يأتي أكمل برهان إحدى حالات نظرية تطابق المثال 3 المتممات. المعطيات: 1 و 3 متتامتان. 22 و 23 متتامتان. و المطلوب : 22 = 1 المبررات ؟ ؟ ؟ ؟ 5 4 6 7 (a (b (c (d (e العبارات البرهان : a 1 و 3 متتامتان. 22 و 23 متتامتان. mZ1 + mZ3 = 90° (b mZ2 + mZ3 = 90° mZ1 + m3 = mZ2 + mZ3 (c m1 = m/2 (d 21 = 22 (e تأكد (5) برهان اكتب برهانا ذا عمودين فيما يأتي: المثال 4 المعطيات: 27 = 4 المطلوب : 26 = 5 تدرب وحل المسائل أوجد قياس الزوايا المرقمة في كل مما يأتي، واذكر النظريات التي تبرر حلك. الأمثلة 3-1 mZ5=mZ6 (6 1) (7) 2 و 3 متتامتان 8 2 و 4 متكاملتان (9) 12 + m29 = (3x 12)° m≤10 = (x − 24)° 24 و 25 متکاملتان mZ4 = 105° 9 23 4/5 10 الدرس 88-1 إثبات علاقات بين الزوايا الت71م Ministry of Education 2024-1446 6 Z1 Z4 mZ2 = 28° 12 4 5

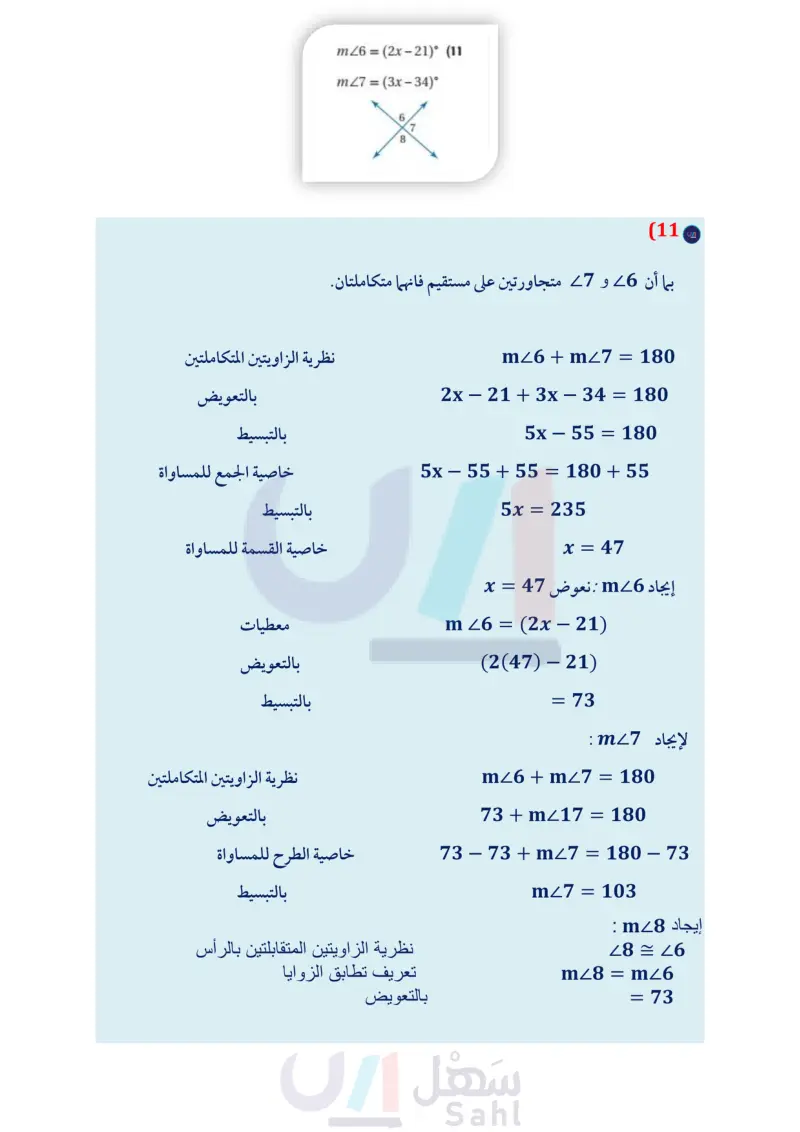
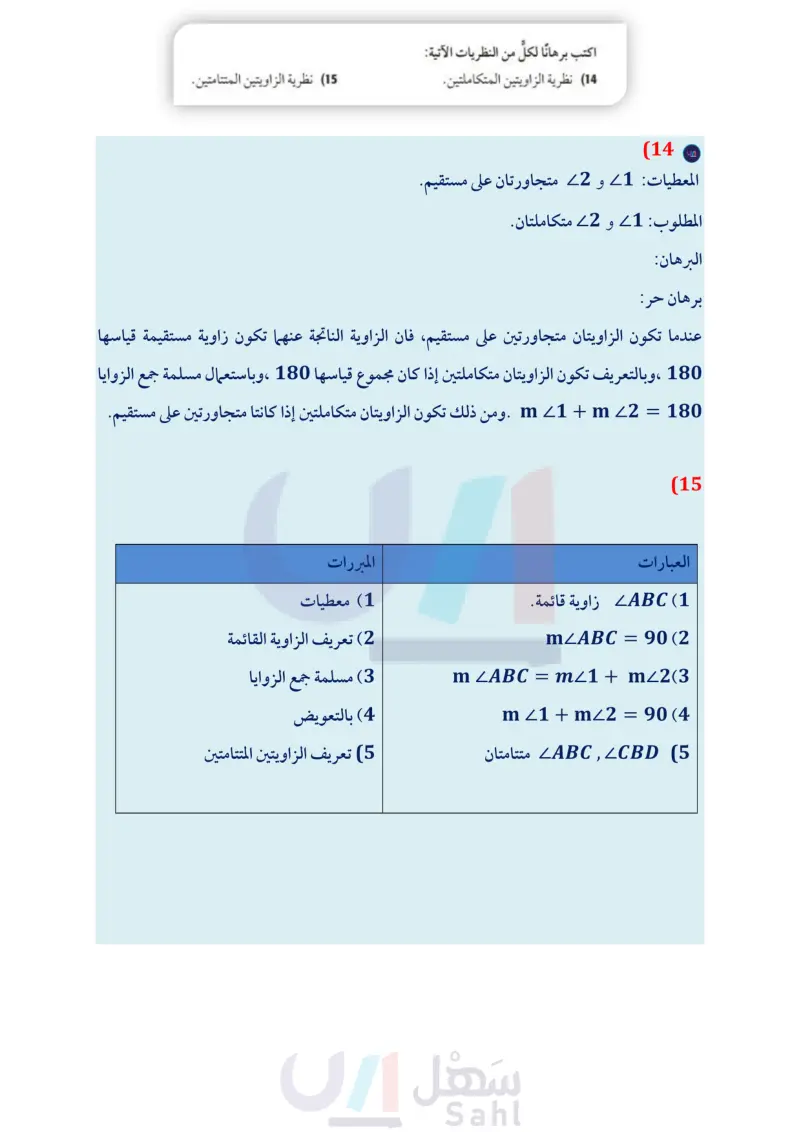
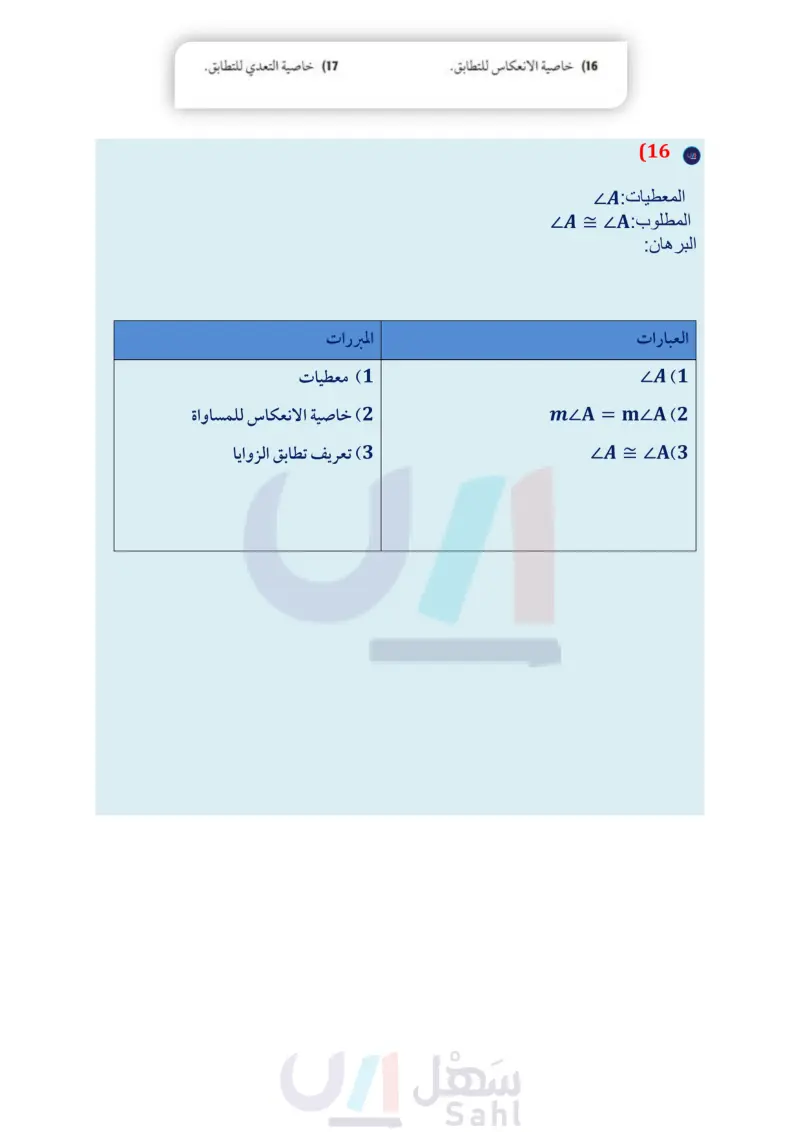
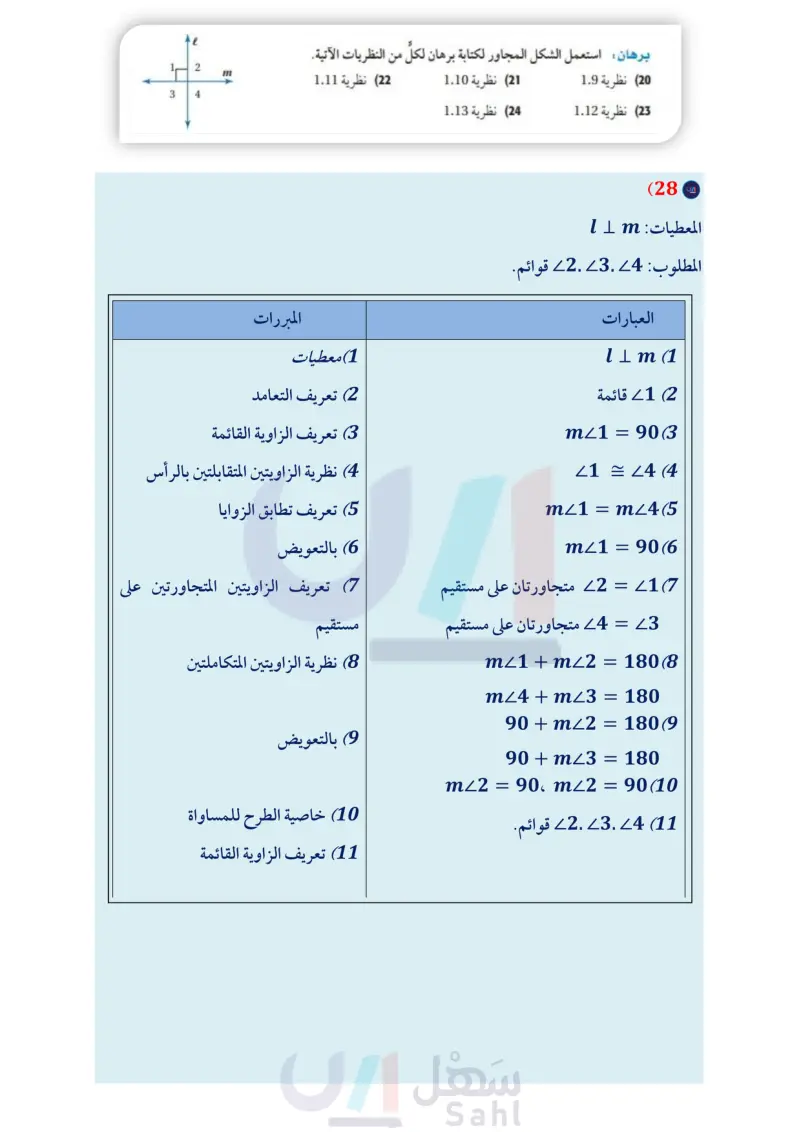
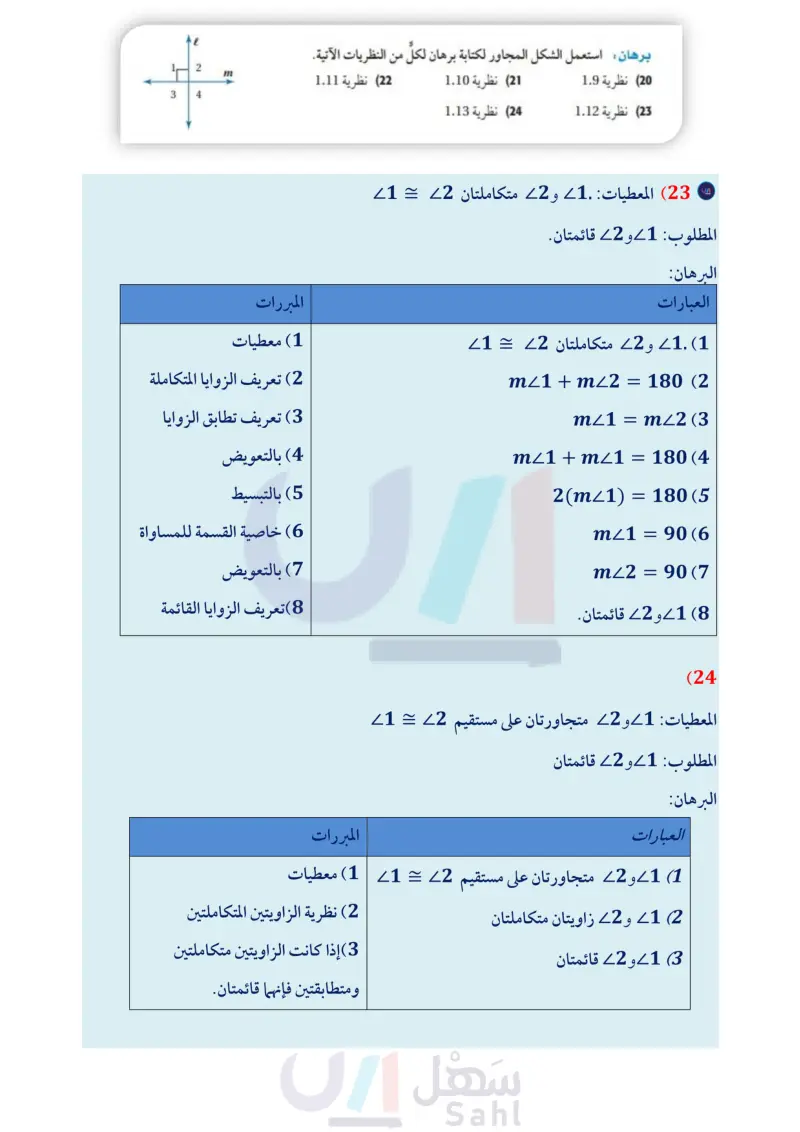
وزارة التعليم Ministry of Education 2024-1446 المثال 4 أوجد قياس الزوايا المرقمة في كل مما يأتي، واذكر النظريات التي تبرر حلك. m26 = (2x-21)° (11 m27=(3x-34)° 8 13) المعطيات: 26 = 5 المطلوب : 46 متكاملتان. ,4 5/4 6 m23 = (2x + 23° (10 m24 = (5x – 112)° 3 برهان اكتب برهانا ذا عمودين في كل مما يأتي: 12 المعطيات: ABC زاوية قائمة. المطلوب : ABD, LCD متتامتان. A D B C الربط مع الحياة يصل طول أنياب الأفعى المجلجلة إلى 6in ، ويمكنها طي أنيابها داخل فمها لتكون موازية لسقف الفم عندما يكون مغلقًا. اكتب برهانا لكل من النظريات الآتية: (14) نظرية الزاويتين المتكاملتين. 16) خاصية الانعكاس للتطابق. (15) نظرية الزاويتين المتتامتين. 17) خاصية التعدي للتطابق. (18) برهان أثبت أن مجموع قياسات الزوايا الأربع الناتجة عند ند فتح المقص يساوي °360 (19) طبيعة : الأفعى المجلجلة أفعى سامة، ويوجد على جلدها زركشة تأخذ أشكالا نمطية. انظر إلى الشكل أدناه، والذي يمثل صورة مكبرة لجلد الأفعى المبينة جهة اليمين. إذا كانت 4 = 1 ، فأثبت أن 23 3 برهان استعمل الشكل المجاور لكتابة برهان لكل من النظريات الآتية. 1 له 2 m 3 4 B Ꭱ (22) نظرية 1.11 (20) نظرية 1.9 (21) نظرية 1.10 (23) نظرية 1.12 (24) نظرية 1.13 (25 بندول يظهر في الشكل المجاور وضع بندول ساعة تقليدية. إذا علمت أن ABC قائمة. وأن °45 = m1 ، فاكتب برهانا حرا لإثبات أن BR ينصف ABC الفصل 1 التبرير والبرهان 72

يصل طول أنياب الأفعى المجلجلة إلى 6in
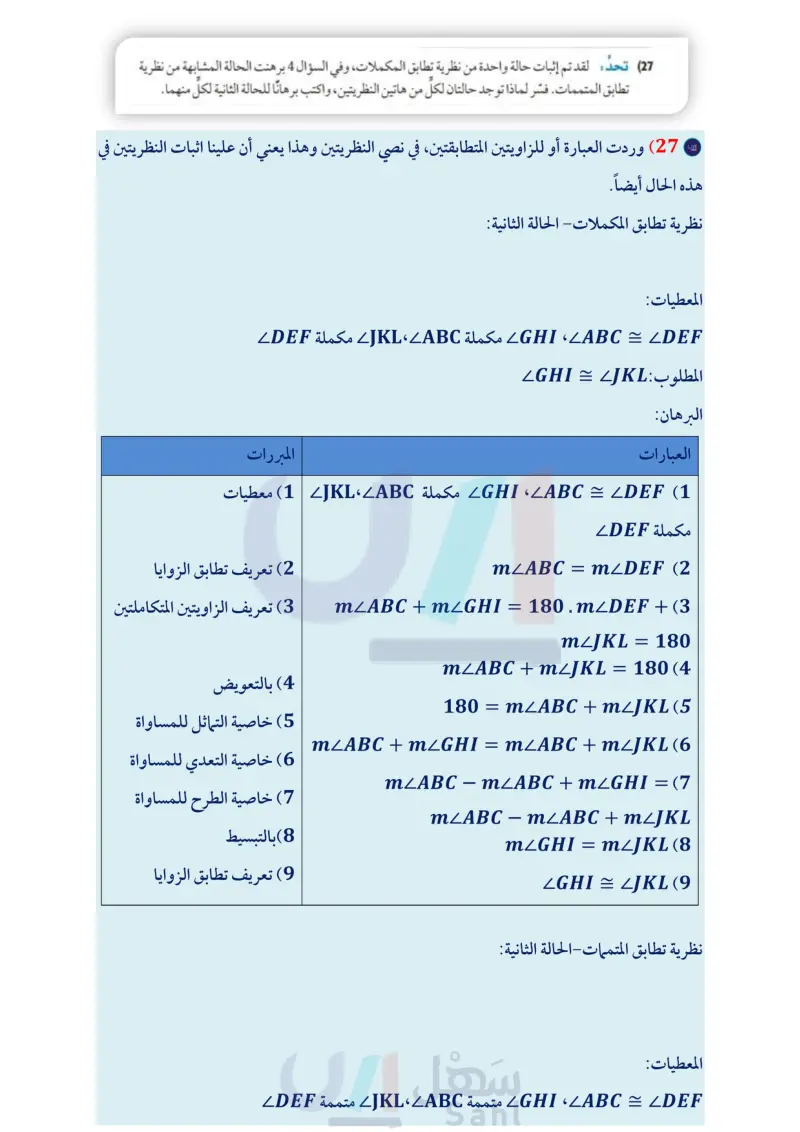
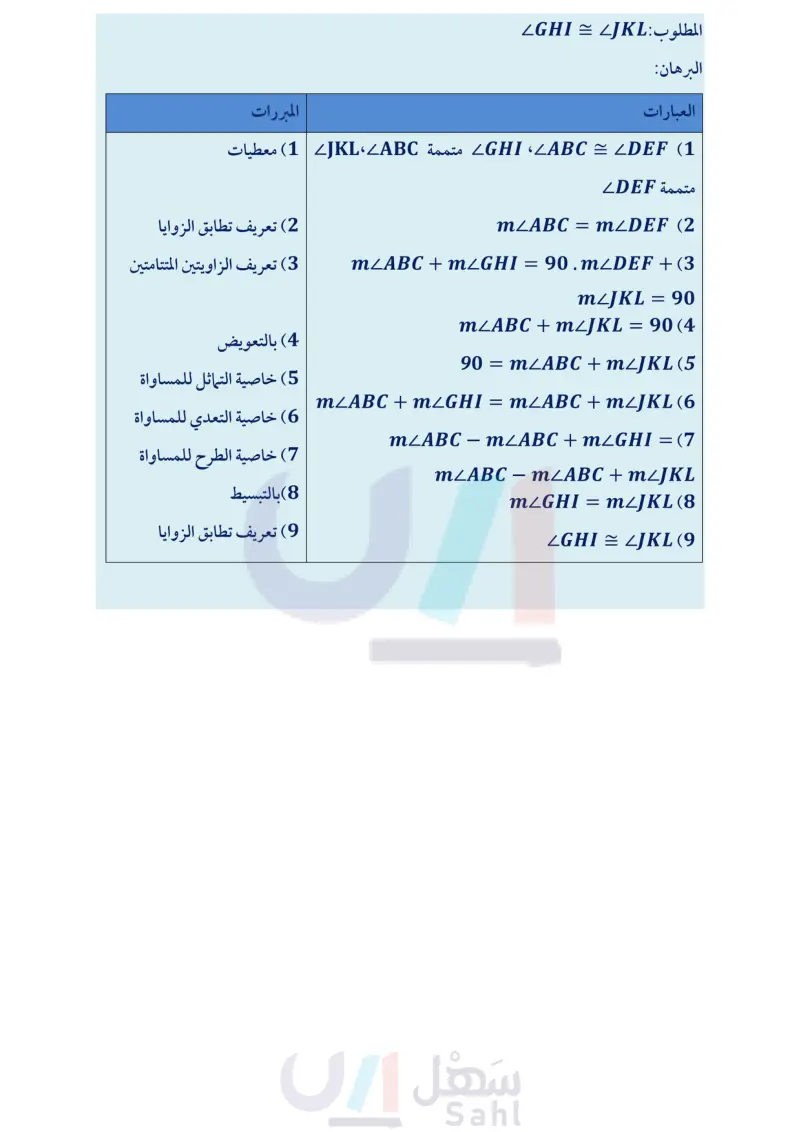
تدريب على اختبار (26) تمثيلات متعددة : تمثيلات متعددة في هذه المسألة سوف تستكشف علاقات الزوايا. ( هندسيا : استعمل المنقلة لرسم زاوية قائمة ABC، وحدد نقطة داخلها، وسمّها .. ارسم BD . b) ثم ارسم KL ، وارسم JKL التي تطابق ABD. لفظيا : ضع تخمينا حول العلاقة بين LJKL و CDBC. منطقيا : أثبت صحة التخمين الذي وضعته. مسائل مهارات التفكير العليا (27) تحد: لقد تم إثبات حالة واحدة من نظرية تطابق المكملات، وفي السؤال 4 برهنت الحالة المشابهة من نظرية تطابق المتممات. فسّر لماذا توجد حالتان لكلِّ من هاتين النظريتين، واكتب برهانا للحالة الثانية لكل منهما. (28) تبرير حدد ما إذا كانت العبارة الآتية صحيحة أحيانًا أو صحيحة دائما أو غير صحيحة أبدًا. فسّر تبريرك. إذا كانت إحدى الزوايا المتكونة من مستقيمين متقاطعين حادة، فإن الزوايا الثلاث الأخرى المتكونة من هذا التقاطع حادة أيضًا. (29) اكتب فسّر كيف يمكن استعمال المنقلة لإيجاد قياس الزاوية المتممة لزاوية أخرى بطريقة سريعة. 30 في الشكل المجاور إذا كانت النقاط ,F, B تقع على استقامة واحدة، وكذلك النقاط A,F,D ، فأوجد قياس LCFD B (31) إذا كانت النسبة بين قياسي زاويتين متتامتين هي 4:1 فما قياس الزاوية الصغرى؟ 15° A 18° B A 42° F 108° 24° C 36° D 0km 0 mi 20 n P • W S R T U F E 108° C 66° A 138° D 72° B مراجعة تراكمية (32) خرائط: يُظهر الشكل المجاور مقياس رسم خريطة تدريجين أحدهما بالكيلومترات، والآخر بالأميال. إذا كانت AB و CD قطعتين مستقيمتين على الخريطة، حيث AB = 100km ، و i AB ، و CD = 62 mi. فهل AB = CD فسّر إجابتك (الدرس 7-1) اذكر الخاصية التي تبرر كل عبارة مما يأتي: (الدرس 6-1 33 إذا كان 5 = 7 + y ، فإن 2 = y (35) إذا كان a - b = x و 3 = b، فإن a – 3 = x استعد للدرس اللاحق استعمل الشكل المجاور للإجابة عما يأتي: (37) سم مستقيما يحوي النقطة P. (39) سمّ نقطة لا تقع على أي من المستقيمات . 40 50 60 80 100 31 62 (34) إذا كان MN = PQ ، فإن PQ = MN (36) إذا كان 4 = + x y ، فإن 4 = xy + xz (38 سم تقاطع المستقيمين n و m. (40) اذكر اسما آخر للمستقيم . (41) هل يتقاطع المستقيم مع المستقيم 17 أو المستقيم ؟ فسر إجابتك. m الدرس 88-1 إثبات علاقات بين الزوايا الت 73م Ministry of Education 2024-1446

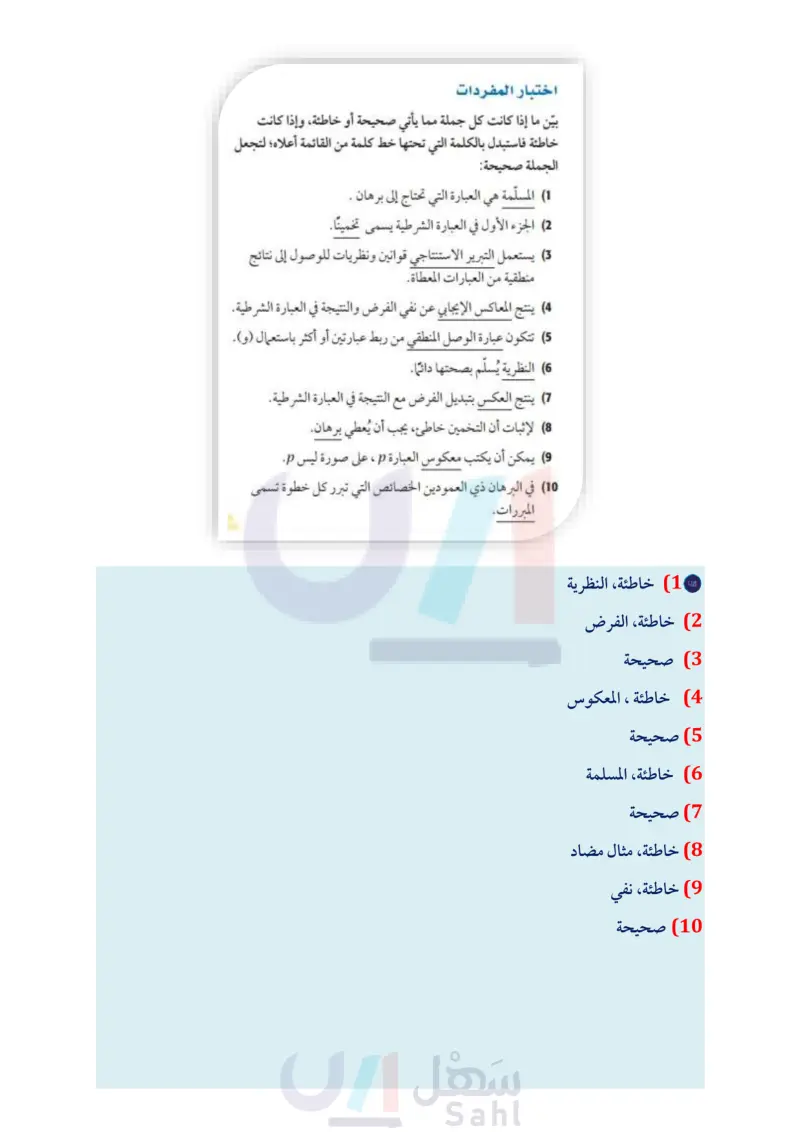
1 دليل الدراسة والمراجعة ملخص الفصل المفاهيم الأساسية التبرير الاستقرائي والمنطق (الدرسان 1-1 و 2-1) . التبرير الاستقرائي : تبرير تُستعمل فيه أمثلة وأنماط محددة للوصول إلى نتيجة. المثال المضاد: هو المثال الذي يُثبت عدم صحة التخمين. . نفي العبارة p: ليس p أو p ~ . عبارة الوصل: عبارة مركبة تحوي (و) • عبارة الفصل: عبارة مركبة تحوي (أو) نفي العبارة (ص. 19) المفردات الأساسية التخمين (ص. (12) العكس (ص. 29) التبرير الاستقرائي (ص. (12) المعكوس (ص. 29) المثال المضاد (ص. 15) قيمة الصواب (ص. 19) العبارة المركبة (ص. 19) العبارات الشرطية المرتبطة (ص. (29) التكافؤ المنطقي (ص. 29) التبرير الاستنتاجي (ص 37) قانون الفصل المنطقي (ص37) قانون القياس المنطقي (ص39) المسلمة (ص.45) البرهان (ص 46) البرهان الحر (ص. 47) النظرية (ص. 47) البرهان الجبري (ص 53) البرهان ذو العمودين (ص. 54) العبارات الشرطية (الدرس (3-1) يمكن كتابة العبارة الشرطية على الصورة (إذا... فإن...) أو على الصورة إذا كان p، فإن q، حيث p الفرض، و و النتيجة. العبارة الشرطية العكس p→ q 4p المعكوس ~p~q ~q→ ~p العبارة (ص. 19) عبارة الوصل (ص. 19) عبارة الفصل (ص. (20) جدول الصواب (ص. (21) النتيجة (ص. (26) العبارة الشرطية (ص. 26) الفرض (ص. (26) المعاكس الإيجابي ( ص 29) اختبار المفردات المعاكس الإيجابي التبرير الاستنتاجي الدرس (4-1) • قانون الفصل المنطقي : إذا كانت العبارة الشرطية p q صائبة، وكانت p صائبة أيضًا ، فإن الصائبة. بين ما إذا كانت كل جملة مما يأتي صحيحة أو خاطئة، وإذا كانت من القائمة أعلاه؛ لتجعل خاطئة فاستبدل بالكلمة التي تحتها خط كلمة . قانون القياس المنطقي: إذا كانت العبارة الشرطية 9 - p صائبة، وكانت q - T صائبة، فإن p - r صائبة أيضًا. البرهان الدروس من 15 إلى (18) . الخطوة 1 اكتب المعطيات وارسم شكلا يوضحها إن أمكن. . الخطوة 2 اكتب العبارة أو التخمين المطلوب إثباته. الخطوة 3 : استعمل التبرير الاستنتاجي لتكوين سلسلة منطقية من العبارات التي تربط المعطيات بالمطلوب. . الخطوة 4 برِّر كل عبارة مستعملا تعريفات أو خصائص جبرية أو مسلمات أو نظريات. • الخطوة 5 اكتب العبارة أو التخمين الذي قمت بإثباته. المطويات منظم أفكار تأكد من أن المفاهيم الأساسية مدونة في مطويتك. المفردات التبرير المنطق العبارات الشرطية البرهان التبرير والبرهان الجملة صحيحة: (1) المسلّمة هي العبارة التي تحتاج إلى برهان . تخمينا. (2) الجزء الأول في العبارة الشرطية يسمى (3) يستعمل التبرير الاستنتاجي قوانين ونظريات للوصول إلى نتائج منطقية من العبارات المعطاة. (4) ينتج المعاكس الإيجابي عن نفي الفرض والنتيجة في العبارة الشرطية. (5) تتكون عبارة الوصل المنطقي من ربط عبارتين أو أكثر باستعمال (و). (6) النظرية يُسلّم بصحتها دائمًا. (7) ينتج العكس بتبديل الفرض مع النتيجة في العبارة الشرطية. (8) لإثبات أن التخمين خاطئ، يجب أن يُعطي برهان. (9) يمكن أن يكتب معكوس العبارة p ، على صورة ليس p. 10 في البرهان ذي العمودين الخصائص التي تبرر كل خطوة تسمى المبررات. 74 الفصل 1 التبرير والبرهان وزارة التعليم Ministry of Education 2024-1446

مراجعة الدروس 1-1 التبرير الاستقرائي والتخمين (ص 18-12) حدد ما إذا كان أي من التخمينين الآتيين صحيحا أو خاطئًا، وإذا كان التخمين خاطئًا، فأعط مثالا مضادًا. (11) إذا كانت 1 و 2 متكاملتين، فإنهما متجاورتان على مستقیم. W(−3,2), X(−3, 7), Y(6, 7), Z(6, 2) ball cubels (12 فإن الشكل الرباعي WXYZ مستطيل. (13) منازل معظم أسطح المنازل في البلدان القريبة من القطب : الشمالي تكون مائلة، بينما تكون مستوية في المناطق الحارة. أعط تخمينا عن سبب اختلاف الأسطح. مثال 1 حدد ما إذا كان أي من التخمينين الآتيين صحيحًا أو خاطئًا، وإذا كان خاطئًا، فأعط مثالا مضادا. d, d = c a = هو مثال على خاصية من خصائص الحقيقية. الأعداد c = d, d = c هو مثال على خاصية التماثل للمساواة في الأعداد الحقيقية. وهذا التخمين صحيح. b) إذا كان AB + CD = AD ، فإن B و C تقعان بین A و D 6 هذا التخمين خاطئ. في الشكل أدناه AB + CD = AD ، ولكن B و C لا تقعان بين A و D 4 2 D 2 له N A 1-2 المنطق (ص 25-19 استعمل العبارات لكتابة كل عبارة وصل أو فصل أدناه ثم أوجد قيمة الصواب لها. فسّر تبريرك. p: يحوي المستوى ثلاث نقاط لا تقع على استقامة واحدة. : الياردة المربعة تكافئ ثلاث أقدام مربعة. مجموع قياسي الزاويتين المتتامتين يساوي 180. ~qvr (14 ~ PA-r (15 ~pvq (16 17) حيوانات أليفة : شكل فن الآتي يُظهر عدد الأشخاص الذين لديهم حيوانات أليفة في منازلهم. قطط 14 42 27 2 20 10 أسماك 10 18 20 طيور مثال 2 استعمل العبارات لكتابة كل عبارة وصل أو فصل أدناه، ثم أوجد قيمة الصواب لها. فسّر تبريرك. x2 :p عدد غير سالب. الزوايا المتجاورة لها ضلع مشترك. العدد السالب ليس عددًا حقيقيًّا. gra gr : الزوايا المتجاورة ليس لها ضلع مشترك، والعدد السالب ليس عددًا حقيقيًّا. بما أن كلا من a و r خاطئتان، فإن r - خاطئة أيضًا. p b أو r p أو x2 : r عدد غير سالب ، أو العدد السالب ليس عددًا ( ما عدد الأشخاص الذين لديهم أسماك فقط ؟ ما عدد الأشخاص الذين لديهم قطط وطيور فقط؟ ما عدد الأشخاص الذين لديهم طيور وأسماك ؟ حقيقيا. p أو r صائبة؛ لأن p صائبة، وليس لكون r خاطئة تأثير. الفصل 1 دليل الدراسة والمراجعة الت75م Ministry of Education 2024-1446

حدد ما إذا كان أي من التخمينين الآتيين صحيحاً أو خاطئاً وإذا كان التخمين خاطئا فأعط مثالا مضادا
أستعمل العبارات لكتابة كل عبارة وصل أو فصل أدناة، ثم اوجد قيمة الصواب لها . فسر تبريرك
1 دليل الدراسة والمراجعة 1-3 العبارات الشرطية ( ص 35-26) حدد قيمة الصواب للعبارتين الشرطيتين الآتيتين، وإذا كانت العبارة صائبة، ففسّر تبريرك ، أما إذا كانت خاطئة فأعط مثالا مضادًا. (18) إذا ربَّعت العدد الصحيح، فإن الناتج يكون عددًا صحيحًا موجبًا. (19) إذا كان للشكل السداسي ثمانية أضلاع، فإن جميع زواياه تكون منفرجة. (20) اكتب العكس والمعكوس والمعاكس الإيجابي للعبارة الشرطية الصائبة الآتية. ثم حدد ما إذا كانت أي منها صائبة أم خاطئة . وإذا كانت خاطئة، فأعط مثالا مضادًا. إذا كانت الزاويتان متطابقتين، فإن لهما القياس نفسه. مثال 3 اكتب العكس والمعكوس والمعاكس الإيجابي للعبارة الشرطية الصائبة الآتية: إذا كان الشكل مربعا فإنه متوازي أضلاع. العكس: المعكوس: إذا كان الشكل متوازي أضلاع، فإنه مربع. إذا لم يكن الشكل مربعا، فإنه ليس متوازي أضلاع. المعاكس الإيجابي: إذا لم يكن الشكل متوازي أضلاع، فإنه ليس مربعًا. 1-4 التبرير الاستنتا جي ( ص 44-37) استعمل قانون الفصل المنطقي أو قانون القياس المنطقي؛ لتحصل على نتيجة صائبة إن أمكن من العبارات الآتية، واذكر القانون الذي استعملته. وإذا تعذر الحصول على نتيجة صائبة، فاكتب "لا نتيجة صائبة". فسّر تبريرك. 21) المعطيات: إذا نصف قطرا الشكل الرباعي كل منهما الآخر، فإن الشكل متوازي أضلاع. ينصف قطرا الشكل الرباعي PQRS كل منهما الآخر. (22) المعطيات: إذا واجهت عائشة صعوبة في مادة العلوم، فإنها ستخصص وقتاً إضافيًا لدراسة المادة. إذا لم تذهب عائشة للسوق، فإنها ستخصص وقتًا إضافيًا لدراسة مادة العلوم. (23) زلازل : حدد ما إذا كانت النتيجة صائبة أم لا فيما يأتي، اعتمادًا على المعطيات. فسّر تبريرك. المعطيات إذا كانت قوة الزلزال 7.0 درجات فأكثر على مقياس ريختر، فإنه يُعتبر زلزالا مدمرًا، ويحدث دمارًا وخرابا كبيرين. كانت قوة زلزال سان فرانسيسكو عام 1906م 8.0 درجات على مقياس ريختر. نتيجة كان زلزال سان فرانسيسكو عام 1906م زلزالًا مدمرًا، وأحدث دمارًا وخرابًا كبيرين. : مثال 4 استعمل قانون الفصل المنطقي أو قانون القياس المنطقي؛ لتحصل على نتيجة صائبة إن أمكن من العبارات الآتية، واذكر القانون الذي استعملته. وإذا تعذر الحصول على نتيجة صائبة فاكتب "لا نتيجة صائبة " . فسّر تبريرك . (1) إذا كان قياس الزاوية أكبر من 90، فإنها منفرجة. (2) إذا كانت الزاوية منفرجة، فإنها ليست قائمة. p قياس الزاوية أكبر من 90 q: الزاوية منفرجة الزاوية ليست قائمة العبارة (1) : p q العبارة (2) : r - 4 بما أن العبارتين الشرطيتين (1) ، (2) صائبتان، فإنه يمكن استنتاج أن r أن p - r؛ باستعمال قانون القياس المنطقي؛ أي أنه إذا كان قياس الزاوية أكبر من °90، فإنها ليست قائمة. 76 الفصل 1 التبرير والبرهان وزارة التعليم Ministry of Education 2024-1446

حدد قيمة الصواب للعبارتين الشرطيتين الآتيتين، وإذا كانت العبارة صائبة ففسر تبريرك، أما إذا كانت خاطئة فأعط مثالا مضادا


استعمل قانون الفصل المنطقي أو قانون القياس المنطقي لتحصل على نتيجة صائبة، إن امكن من العبارات الآتية


استعمل قانون الفصل المنطقي أو قانون القياس المنطقي لتحصل على نتيجة صائبة، إن امكن من العبارات الاتية
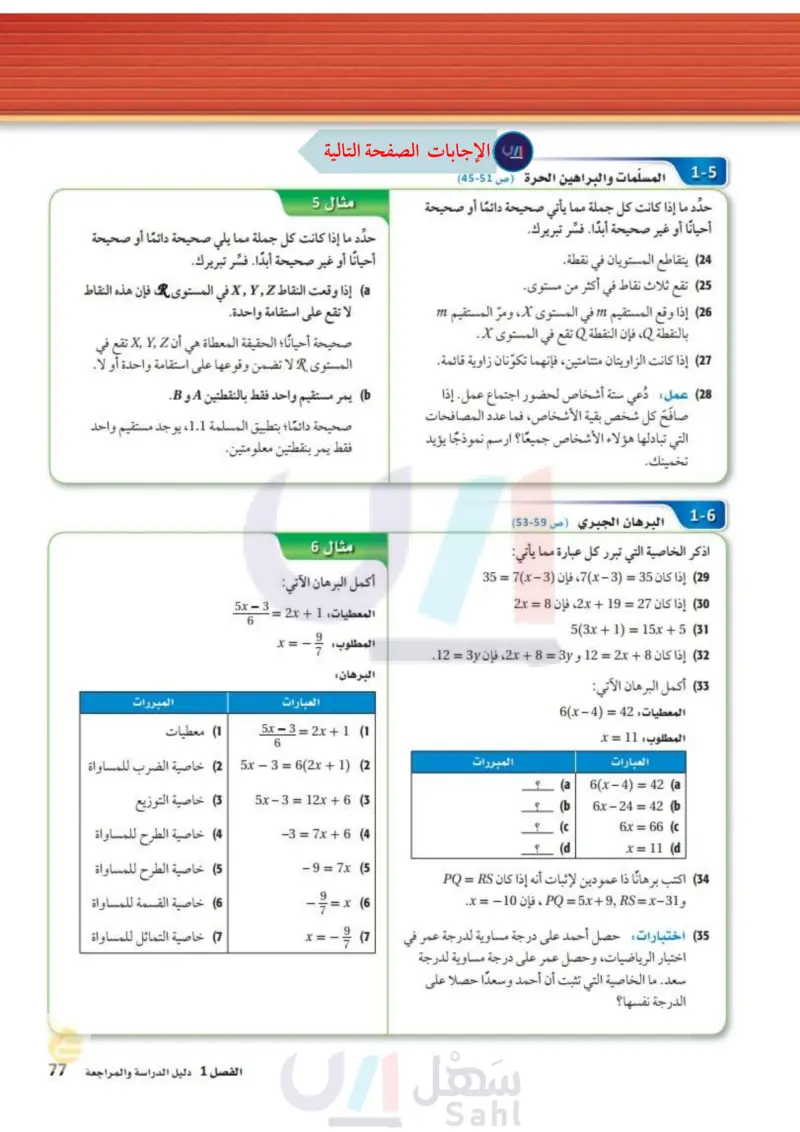
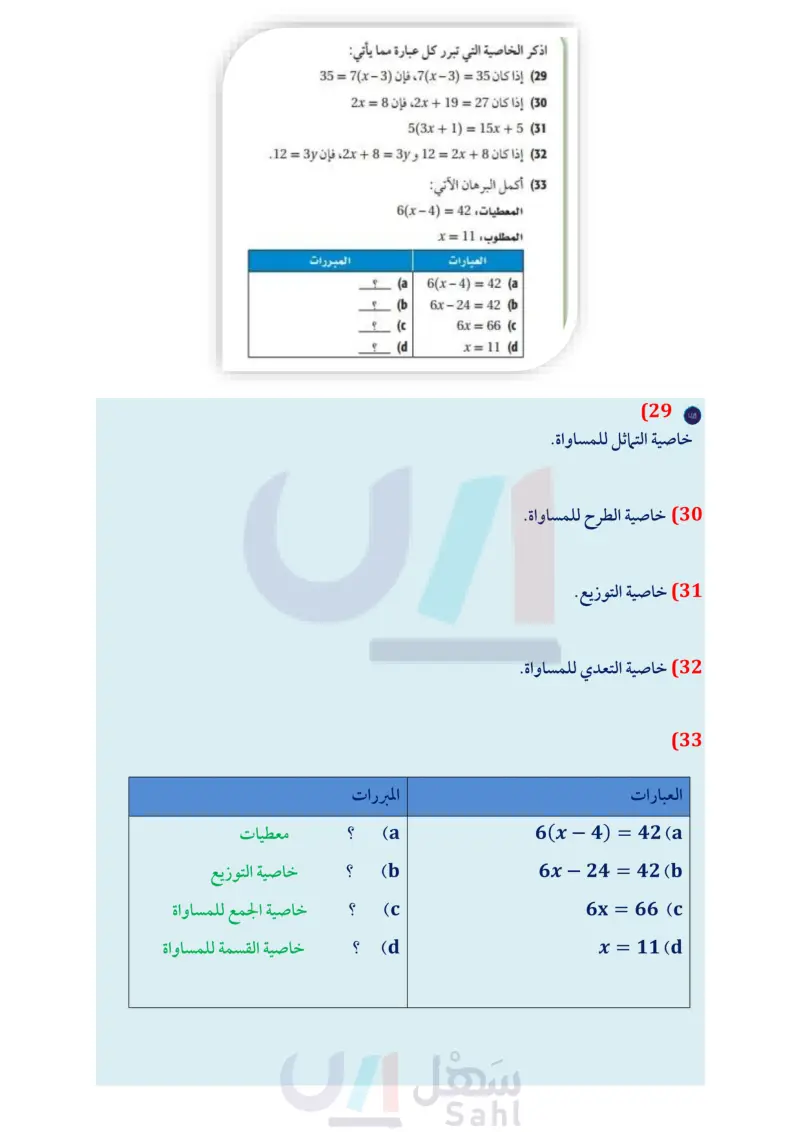
1-5 المسلمات والبراهين الحرة ( ص 51-45 حدد ما إذا كانت كل جملة مما يأتي صحيحة دائمًا أو صحيحة أحيانًا أو غير صحيحة أبدًا. فسّر تبريرك. (24) يتقاطع المستويان في نقطة. (25) تقع ثلاث نقاط في أكثر من مستوى. (26) إذا وقع المستقيم 111 في المستوى X، ومرّ المستقيم m بالنقطة Q، فإن النقطة Q تقع في المستوى X. (27) إذا كانت الزاويتان متتامتين، فإنهما تكونان زاوية قائمة. (28) عمل: دعي ستة أشخاص لحضور اجتماع عمل. إذا صافَحَ كل شخص بقية الأشخاص، فما عدد المصافحات التي تبادلها هؤلاء الأشخاص جميعًا؟ ارسم نموذجا يؤيد تخمينك. مثال 5 حدد ما إذا كانت كل جملة مما يلي صحيحة دائمًا أو صحيحة أحيانًا أو غير صحيحة أبدًا. فسّر تبريرك. , a إذا وقعت النقاط في المستوى ، فإن هذه النقاط لا تقع على استقامة واحدة. صحيحة أحيانًا؛ الحقيقة المعطاة هي X,Y,Z أن تقع في المستوى A لا تضمن وقوعها على استقامة واحدة أو لا. يمر مستقيم واحد فقط بالنقطتين A و B . صحيحة دائمًا؛ بتطبيق المسلمة ،11، يوجد مستقيم واحد فقط يمر بنقطتين معلومتين. 1-6 البرهان الجبري ص 5359 اذكر الخاصية التي تبرر كل عبارة مما يأتي: - (29) إذا كان 35 = (3) x ) ، فإن (3) - x) = 35 (30) إذا كان 27 = 19 + 2x، فإن 8 = 2x 5(3x + 1) = 15x + 5 (31 (32) إذا كان 8 + 2x = 12 و 2x + 8 = 3y، فإن 3y = 12. (33) أكمل البرهان الآتي: المعطيات 42 = 4 - 6x المطلوب : 11 = x العبارات المبررات ؟ مثال 6 أكمل البرهان الآتي: المعطيات: 1 + 2x = 9 7 5x − 3 6 x = - المطلوب : و - البرهان : العبارات 5x-3=2x+1 (1 6 5x - 3 = 6(2x + 1) (2 (a 6(x-4)=42 (a (b 6x - 24 = 42 (b (c 6x = 66 (c (d x = 11 (d ؟ (34) اكتب برهانا ذا عمودين لإثبات أنه إذا كان PQ = RS و 31 - PQ = 5x + 9, RS = x ، فإن 10- = x. 35 اختبارات حصل أحمد على درجة مساوية لدرجة عمر في اختبار الرياضيات، وحصل عمر على درجة مساوية لدرجة سعد ما الخاصية التي تثبت أن أحمد وسعدًا حصلا على الدرجة نفسها؟ 5x - 3 = 12x + 6 (3 -3 = 7x + 6 (4) -9=7x (5 17 9 = (6 x = 17 9 (7 المبررات 1) معطيات (2 خاصية الضرب للمساواة (3) خاصية التوزيع (4) خاصية الطرح للمساواة (5) خاصية الطرح للمساواة (6) خاصية القسمة للمساواة (7) خاصية التماثل للمساواة الفصل 1 دليل الدراسة والمراجعة الت77م Ministry of Education 2024-1446

حدد ما إذا كانت كل جملة مما يأتي صحيحة دائماً أو صحيحة احيانا او غير صحيحة أبدا. فسر تبريرك
أكمل البرهان الاتي
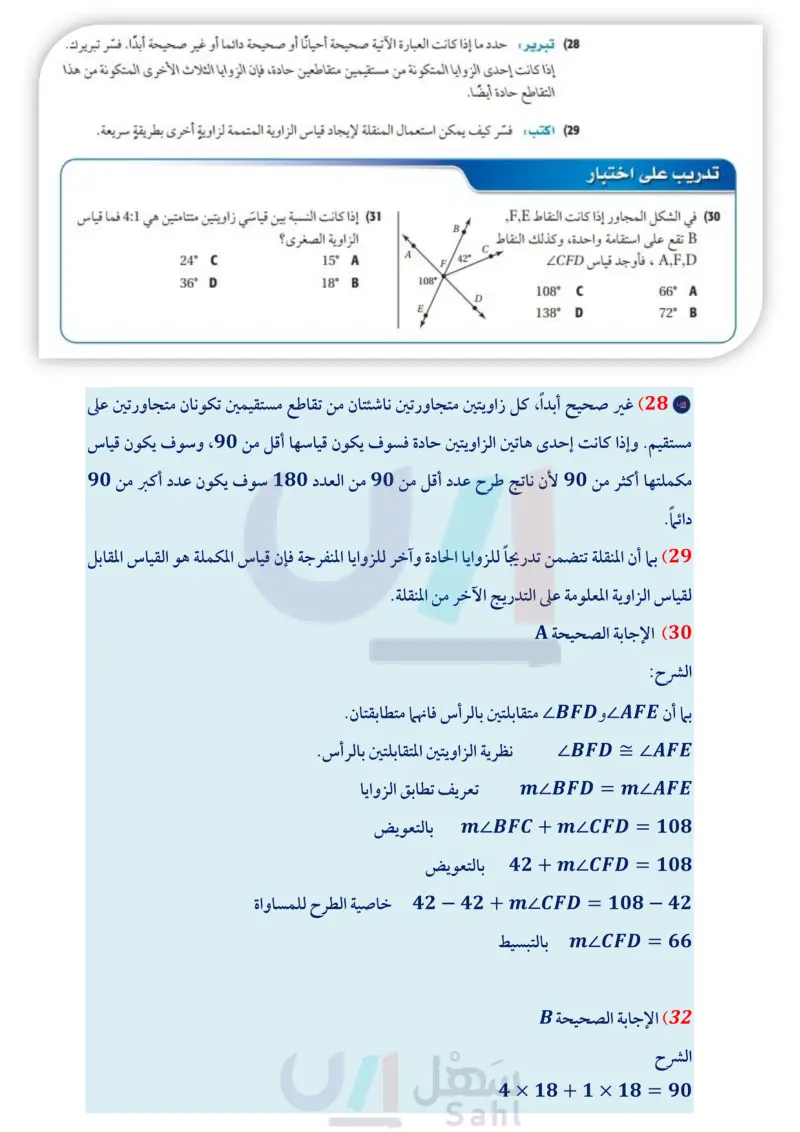
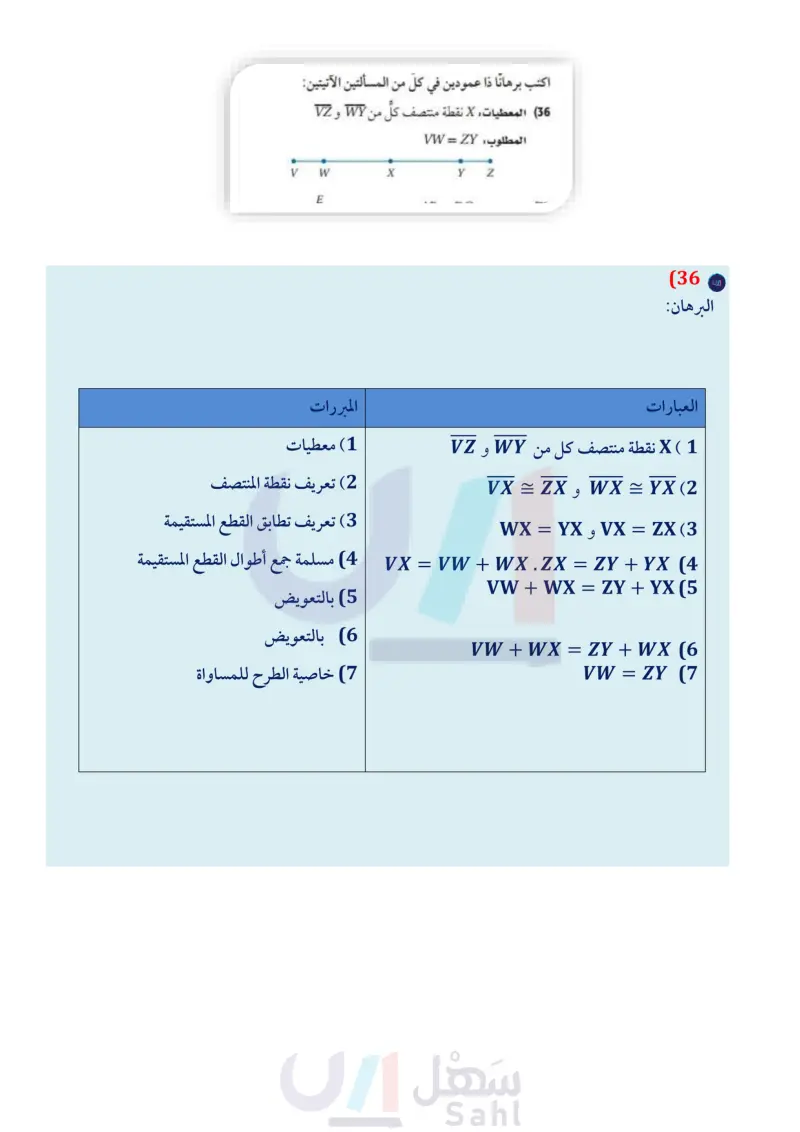
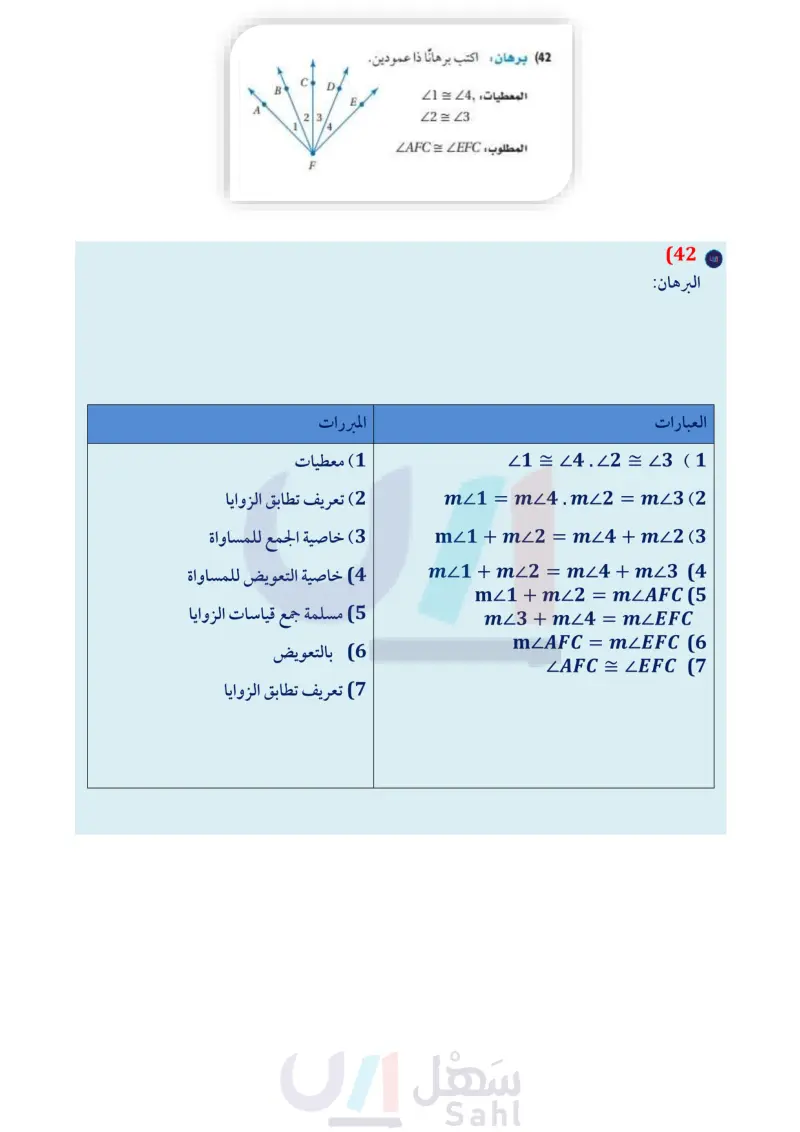
78 1 دليل الدراسة والمراجعة 1-7 إثبات العلاقات بين القطع المستقيمة (ص 65-60) اكتب برهانا ذا عمودين في كلّ من المسألتين الآتيتين: 36 المعطيات : X نقطة منتصف كل من WY و VZ المطلوب : VW = ZY مثال 7 اكتب برهانا ذا عمودين. المعطيات: B نقطة منتصف AC Y Z 37 المعطيات : AB = DC المطلوب : AC = DB V W X E C D C نقطة منتصف BD المطلوب : AB = CD البرهان : العبارات D C المبررات 1 نقطة منتصف AC 1) معطيات A B AB = BC (4) 38 جغرافيا: أراد طارق السفر من مدينة جدة إلى الطائف، مرورًا بمكة المكرمة لاصطحاب أخيه. ويعلم أن المسافة من من جدة إلى مكة المكرمة تساوي 79km ، والمسافة مكة المكرمة إلى الطائف تساوي 88km، استنتج سيقطع 167km في هذه الرحلة. فسر كيف استنتج ذلك؟ افترض أن الطريق الذي يربط هذه المدن الثلاث يشكل مستقيما . 1-8 إثبات علاقات بين الزوايا (ص 73-66) أوجد قياس كل زاوية فيما يأتي: 25 (39 Z6 (40 27 (41 (42) برهان اكتب برهانا ذا عمودين. المعطيات 24 = 21 22 = 23 المطلوب : ZAFC = LEFC الفصل 1 التبرير والبرهان (3 نقطة منتصف BD أنه BC= CD (4 AB = CD (5) t 5 6/7 53% C⚫ D B E A 23 B (2) نظرية نقطة المنتصف (3) معطيات (4) نظرية نقطة المنتصف (5) خاصية التعدي للتطابق مثال 8 إذا علمت أن : 26 = m1 = 72°, m3 ، فأوجد قياس كل زاوية مرقمة في الشكل أدناه. 1 2 3 4 72° = 2 ؛ لأن 12 متقابلتان بالرأس. , متجاورتان على مستقيم؛ إذن فهما متكاملتان. F 26° + mZ4 = 180° mZ4 = 154° تعريف الزاويتين المتكاملتين بطرح 26 من كلا الطرفين A وزارة التعليم Ministry of Education 2024-1446

اكتب برهانا ذا عمودين
أوجد قياس كل زاوية مرقمة في الشكل أدناه
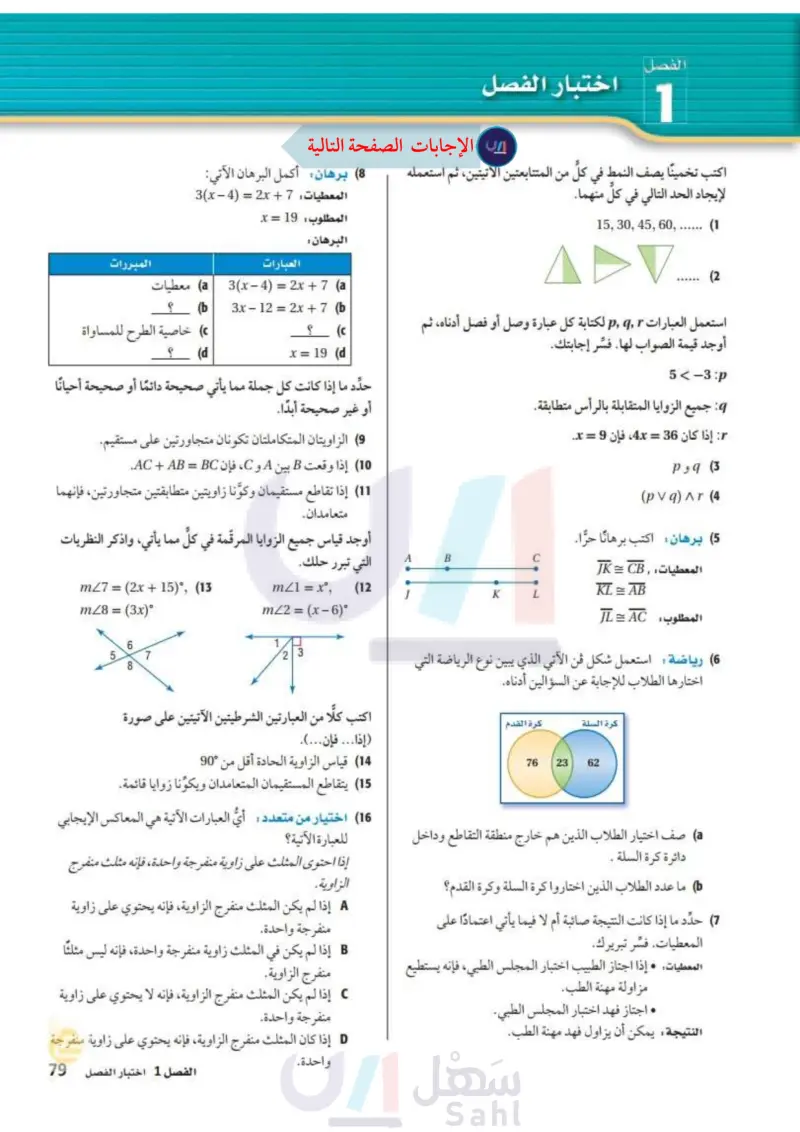
1 اختبار الفصل اكتب تخمينا يصف النمط في كلّ من المتتابعتين الآتيتين، ثم استعمله 8 برهان : أكمل البرهان الآتي: لإيجاد الحد التالي في كل منهما. ... (1 (2 15, 30, 45, 60, ADV المعطيات: 7 + x - 4 = 2x) المطلوب : 19 = x البرهان : العبارات 3(x-4)=2x+7 (a المبررات a معطيات ؟ استعمل العبارات لكتابة كل عبارة وصل أو فصل أدناه، ثم أوجد قيمة الصواب لها. فسّر إجابتك. 5 < -3 :p : جميع الزوايا المتقابلة بالرأس متطابقة. إذا كان 36 = 4x، فإن 9 = x. 3 a و p (pv q) ^r (4 (5) برهان اكتب برهانًا حرا. المعطيات,JK = CB C B A (b 3x - 12 = 2x + 7 (b ؟ (d x = 19 (d خاصية الطرح للمساواة ؟ حدد ما إذا كانت كل جملة مما يأتي صحيحة دائمًا أو صحيحة أحيانًا أو غير صحيحة أبدًا. (9) الزاويتان المتكاملتان تكونان متجاورتين على مستقيم. (10) إذا وقعت B بين A و C ، فإن AC + AB = BC. (11) إذا تقاطع مستقيمان وكونا زاويتين متطابقتين متجاورتين، فإنهما متعامدان أوجد قياس جميع الزوايا المرقمة في كلُّ مما يأتي، واذكر النظريات التي تبرر حلك. KL = AB المطلوب : JL = AC K L (6) رياضة: استعمل شكل فن الآتي الذي يبين نوع الرياضة التي اختارها الطلاب للإجابة عن السؤالين أدناه. كرة السلة كرة القدم 29 76 23 62 76 صف اختيار الطلاب الذين هم خارج منطقة التقاطع وداخل دائرة كرة السلة . ما عدد الطلاب الذين اختاروا كرة السلة وكرة القدم؟ (7) حدد ما إذا كانت النتيجة صائبة أم لا فيما يأتي اعتمادًا على المعطيات. فسّر تبريرك. المعطيات: إذا اجتاز الطبيب اختبار المجلس الطبي، فإنه يستطيع مزاولة مهنة الطب. اجتاز فهد اختبار المجلس الطبي. النتيجة يمكن أن يزاول فهد مهنة الطب. m27 = (2x+15)°, (13 mZ8 = (3x)° m/1 = x°, mZ2 = (x - 6)° (12 J CO LO 6 5 7 8 23 اكتب كلا من العبارتين الشرطيتين الآتيتين على صورة (إذا ... فإن...). 14) قياس الزاوية الحادة أقل من 90° (15) يتقاطع المستقيمان المتعامدان ويكونا زوايا قائمة. (16) اختيار من متعدد: أيُّ العبارات الآتية هي المعاكس الإيجابي للعبارة الآتية؟ إذا احتوى المثلث على زاوية منفرجة واحدة، فإنه مثلث منفرج الزاوية. إذا لم يكن المثلث منفرج الزاوية، فإنه يحتوي على زاوية منفرجة واحدة. إذا لم يكن في المثلث زاوية منفرجة واحدة، فإنه ليس مثلثا منفرج الزاوية. إذا لم يكن المثلث منفرج الزاوية، فإنه لا يحتوي على زاوية منفرجة واحدة. إذا كان المثلث منفرج الزاوية، فإنه يحتوي على زاوية منفرجة واحدة. الفصل 1 اختبار الفصل الت79م Ministry of Education 2024-1446

1 الإعداد للاختبارات التبرير المنطقي أحيانًا كثيرة يتطلب حل مسائل الهندسة استعمال التبريرات المنطقية؛ لذا يمكنك استعمال أساسيات التبرير المنطقي في حل مسائل الاختبارات. استراتيجيات استعمال التبرير المنطقي الخطوة 1 اقرأ المسألة لتحدد المعطيات، وما يجب أن تجده للإجابة عن السؤال. الخطوة 2 حدد هل بإمكانك تطبيق أحد مبادئ التبرير المنطقي في هذه المسألة. • المثال المضاد المثال المضاد هو المثال الذي يناقض عبارة يُفترض أنها صائبة. حدد بدائل الإجابة التي تراها مناقضةً لنص المسألة واحذفها. . المسلمات المسلّمة هي عبارة تصف علاقة أساسية في الهندسة. حدد هل بإمكانك تطبيق مسلّمة للتوصل إلى نتيجة منطقية. m الخطوة 3 إذا لم تصل إلى أي نتيجة من مبادئ الخطوة 2 فحدد ما إذا كانت الأدوات الآتية تساعدك على الحل أم لا. . الأنماط ابحث عن نمط لعمل تخمین مناسب. . جداول الصواب: استعمل جدول صواب لتنظيم قيم الصواب للعبارات المعطاة في المسألة. . أشكال فن : استعمل أشكال فن لتمثيل العلاقات بين عناصر المجموعات بوضوح. • البراهين استعمل التبرير الاستقرائي والتبرير الاستنتاجي للوصول إلى نتيجة على شكل برهان. الخطوة 4 إذا لم يكن بإمكانك الوصول إلى نتيجة حتى باستعمال مبادئ الخطوة ،3 فخمن بديل الإجابة الأنـ ضع علامة على السؤال حتى ترجع إليه إذا بقي متسع من الوقت في نهاية الاختبار. 80 80 الفصل 1 التبرير والبرهان ثم وزارة التعليم Ministry of Education 2024-1446

استراتيجيات استعمال التبرير المنطقي
مثال اقرأ المسألة جيدًا، وحدّد المطلوب فيها . ثم استعمل المعطيات لحلها. عدد طلاب مدرسة 292 طالبًا، شارك 94 منهم في الألعاب الرياضية ، و 122 في النوادي الثقافية، و 31 في كليهما. كم طالبًا لم يشارك في الألعاب الرياضية أو في النوادي الثقافية؟ 95 A 107 B 122 C 138 D اقرأ المسألة جيدًا. من الواضح أنه ليس هناك أمثلة مضادة واضحة، ولا يمكن استعمال المسلمات للوصول إلى نتيجة منطقية؛ إذن علينا استعمال أدوات لتنظيم المعلومات المعطاة؛ لنراها بوضوح. يمكننا رسم شكل فن لنرى التقاطع بين المجموعتين، وتحديد معطيات السؤال على هذا الشكل. حدد عدد الطلاب الذين شاركوا في الألعاب الرياضية أو في النوادي الثقافية فقط. الألعاب الرياضية فقط : 63 = 31 – 94 النوادي الثقافية فقط : 91 = 31 – 122 استعمل هذه المعلومات لحساب عدد الطلاب الذين لم يشاركوا في الألعاب الرياضية ولا في النوادي الثقافية. 29263 91 - 31 = 107 — النشاطات المدرسية النوادي الثقافية الألعاب الرياضية 107 63 31 91 إذن عدد الطلاب الذين لم يشاركوا في الألعاب الرياضية ولا في النوادي الثقافية يساوي 107 طلاب طلاب. وعليه فالإجابة الصحيحة هي .B تمارين ومسائل اقرأ كل سؤال مما يأتي، ثم اكتب رمز الإجابة الصحيحة. (1) حدد قيمة الصواب للعبارة الآتية. وإذا كانت خاطئة، فأعط مثالا مضادا. ناتج ضرب عددين زوجيين هو عدد زوجي. A خاطئة 32 = 4 × 8 خاطئة؛ 42 = 6 × 7 خاطئة ؛ 30 = 10 × 3 (2) أوجد الحد التالي في النمط أدناه. A B :: D صحيحة C D الفصل 1 الإعداد للاختبارات الت81 م Ministry of Education 2024-1446

اقرأ المسألة جيدا وحدد المطلوب فيها. ثم استعمل المعطيات لحلها عدد طلاب مدرسة 292 طالبا
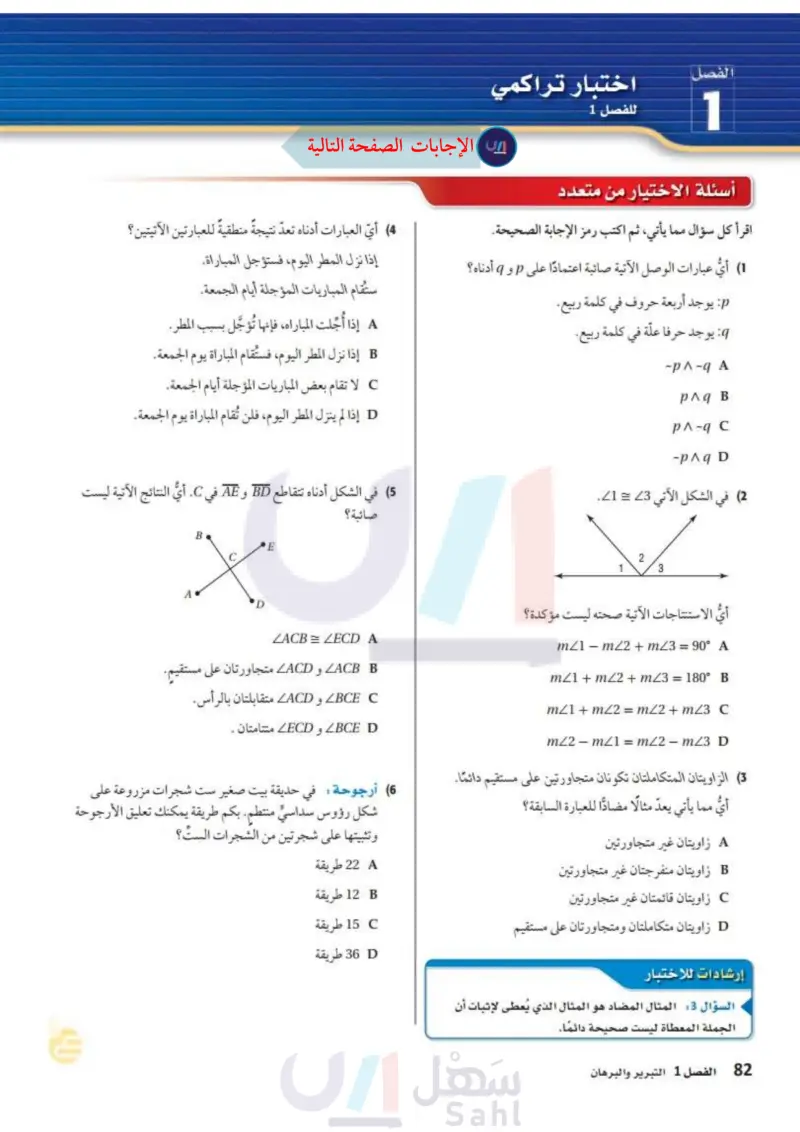
اختبار تراكمي للفصل 1 1 أسئلة الاختيار من متعدد اقرأ كل سؤال مما يأتي، ثم اكتب رمز الإجابة الصحيحة. 1) أيُّ عبارات الوصل الآتية صائبة اعتمادًا على p و q أدناه؟ p: يوجد أربعة حروف في كلمة ربيع. يوجد حرفا علة في كلمة ربيع. ~p-q A рлд в (4) أيّ العبارات أدناه تعدّ نتيجةً منطقيةً للعبارتين الآتيتين؟ إذا نزل المطر اليوم، فستؤجل المباراة. ستقام المباريات المؤجلة أيام الجمعة. A إذا أُجلت المباراة، فإنها تُؤجل بسبب المطر. إذا نزل المطر اليوم، فستقام المباراة يوم الجمعة. C لا تقام بعض المباريات المؤجلة أيام الجمعة. D إذا لم ينزل المطر اليوم، فلن تُقام المباراة يوم الجمعة. -pqD (2) في الشكل الآتي 3 = 1. (5) في الشكل أدناه تتقاطع BD و AE في C. أيُّ النتائج الآتية ليست صائبة؟ A B X D E LACB = LECD A ACB B و ACD متجاورتان على مستقيم. BCE C و ACD متقابلتان بالرأس. BCE D و LECD متتامتان . 2 1 3 أيُّ الاستنتاجات الآتية صحته ليست مؤكدة؟ mZ1 - mZ2 + mZ3 = 90° A mZ1 + mZ2 + mZ3 = 180° B mZ1+mZ2 = mZ2 + m Z3 C mz2mZ1 = mZ2 - mZ3 D (3) الزاويتان المتكاملتان تكونان متجاورتين على مستقيم دائما . أيُّ مما يأتي يعدّ مثالًا مضادا للعبارة السابقة؟ A زاویتان غير متجاورتين B زاویتان منفرجتان غير متجاورتين C زاویتان قائمتان غير متجاورتين D زاويتان متكاملتان ومتجاورتان على مستقيم إرشادات للاختبار السؤال 3 : المثال المضاد هو المثال الذي يُعطى لإثبات أن الجملة المعطاة ليست صحيحة دائمًا. 6 أرجوحة في حديقة بيت صغير ست شجرات مزروعة على شكل رؤوس سداسي منتظم. بكم طريقة يمكنك تعليق الأرجوحة وتثبيتها على شجرتين من الشجرات الست؟ A 22 طريقة 12 طريقة C 15 طريقة D 36 طريقة وزارة التعليم Ministry of Education 2024-1446 الفصل 1 التبرير والبرهان 82

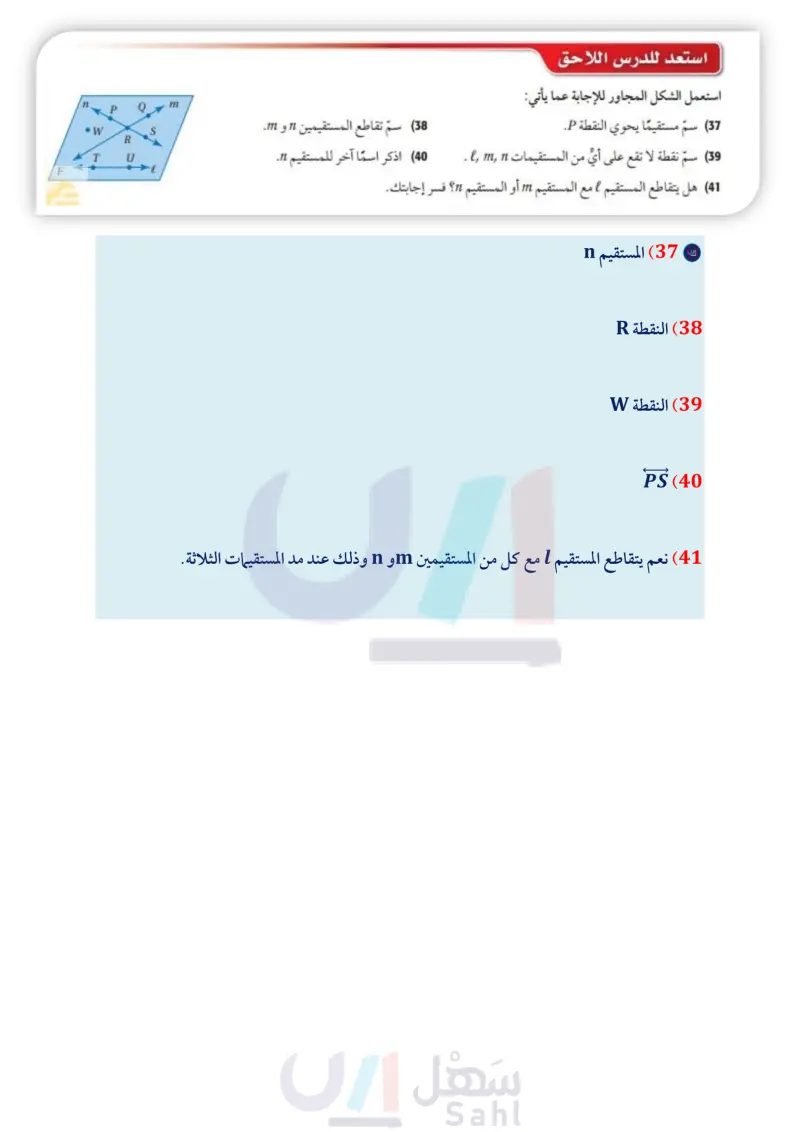
في الشكل الآتي أي الاستنتاجات الآتية صحته ليست مؤكدة؟
أي مما يأتي يعد مثالا مضادا للعبارة السابقة د؟
أي العبارات أدناه تعد نتيجة منطقية للعبارتين الآتيتين؟
في الشكل أدناه أي النتائج الآتية ليست صائية؟
بكم طريقة يمكنك تعليق الأرجوحة وتثبيتها على شجرتين من الشجرات الست؟
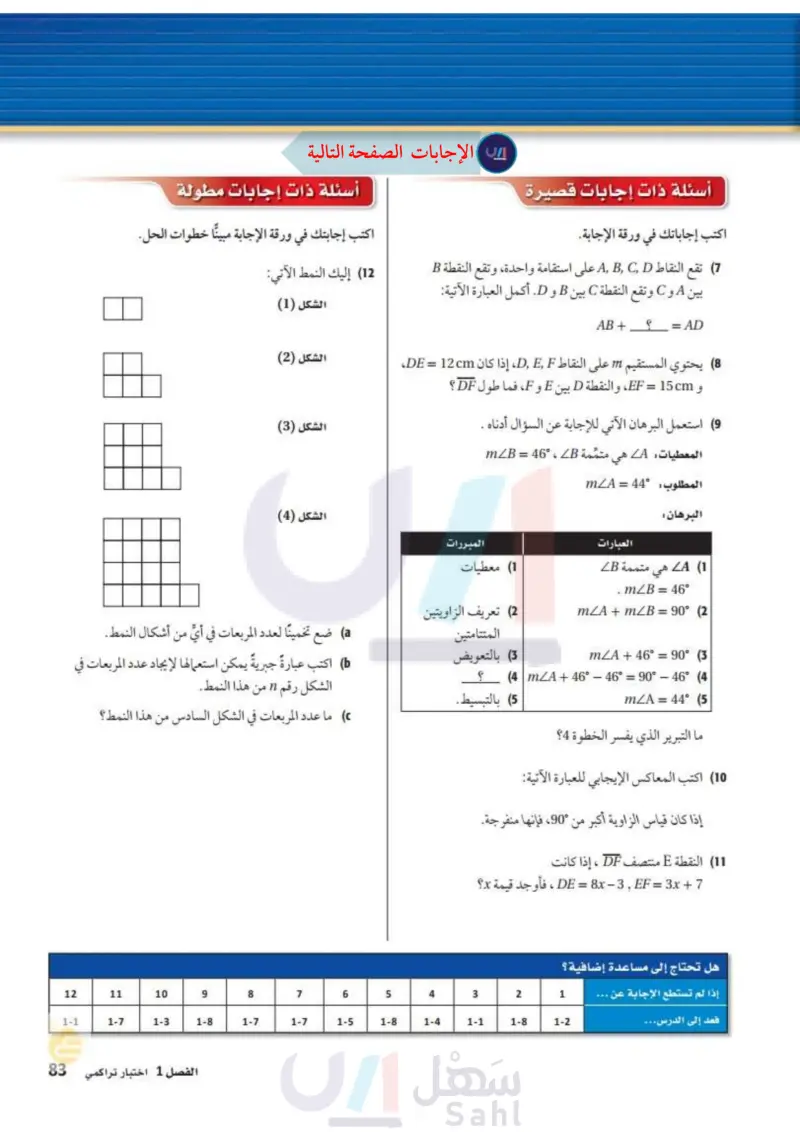
أسئلة ذات إجابات قصيرة اكتب إجاباتك في ورقة الإجابة. (7) تقع النقاط على استقامة واحدة، وتقع النقطة B بین A و C وتقع النقطة C بين B و D. أكمل العبارة الآتية: AB + = AD (8) يحتوي المستقيم 171 على النقاط , إذا كان DE = 12cm، و EF = 15 cm ، والنقطة بين E و F، فما طول DF؟ و استعمل البرهان الآتي للإجابة عن السؤال أدناه . هي المعطيات A متمّمة mZB = 46° ، B المطلوب °44 = mLA 6 البرهان : LA (1 هي العبارات متممة B . mZB = 46° mZA + mZB = 90° (2 أسئلة ذات إجابات مطولة اكتب إجابتك في ورقة الإجابة مبينا خطوات الحل. (13) إليك النمط الآتي: الشكل (1) الشكل (2) الشكل (3) الشكل (4) المبررات 1) معطيات (2) تعريف الزاويتين المتتامتين (3) بالتعويض ( ضع تخمينا لعدد المربعات في أي من أشكال النمط. ( اكتب عبارةً جبريةً يمكن استعمالها لإيجاد عدد المربعات في الشكل رقم n من هذا النمط . mZA + 46° = 90° (3 (4 | mZA + 46° - 46° = 90° - 46° (4 = 44° (5 mZA ما التبرير الذي يفسر الخطوة 4؟ (10) اكتب المعاكس الإيجابي للعبارة الآتية: ؟ (5) بالتبسيط. إذا كان قياس الزاوية أكبر من 90، فإنها منفرجة. 11) النقطة E منتصف DF ، إذا كانت 7 + DE = 8x - 3, EF = 3x ، فأوجد قيمة x؟ (12) اكتب عكس العبارة الآتية: إذا كنت الرابح، فأنا الخاسر“. هل تحتاج إلى مساعدة إضافية ؟ ما عدد المربعات في الشكل السادس من هذا النمط ؟ إذا لم تستطع الإجابة عن . فعد إلى الدرس... 13 12 11 10 8 7 6 5 4 3 2 1 1-1 1-7 1-3 1-8 1-3 1-7 1-7 1-5 1-8 1-4 1-1 1-8 1-2 الفصل 1 اختبار تراكمي الت 83 - Ministry of Education 2024-1446




 0
0 

 1
1 

 0
0 

 2
2