الأشكال المتشابهة - الرياضيات 3 - أول متوسط

ΠΑ ۷-۸ الأشكال المتشابهة نشاط رابط الدرس الرقمي www.ien.edu.sa فكرة الدرس : أحدد ما إذا كانت الأشكال متشابهة، وأجد الطول المجهول في شكلين متشابهين. المفردات: الأشكال المتشابهة الأضلاع المتناظرة الزوايا المتناظرة القياس غير المباشر قراءة الرياضيات رموز هندسية أب : طول القطعة المستقيمة أب. المستطيلان أدناه لهما الشكل نفسه، ولكن بقياسات مختلفة. وكذلك المثلثان. انسخ الأشكال على ورقة منقطة، ثم أوجد قياس كل زاوية باستعمال المنقلة، وطول كل ضلع باستعمال المسطرة. مل في المستطيل الصغير تقابل هـ و في المستطيل الكبير. جميع أزواج الأضلاع المتقابلة في كل من المستطيلين والمثلثين. كل نسبة مما يأتي في أبسط صورة: ماذا تلاحظ على نسب الأضلاع المتقابلة؟ اسم كل زوج من الزوايا المتقابلة في كل من المستطيلين والمثلثين. ماذا تلاحظ على قياسات هذه الزوايا؟ القطعة المستقيمة التي طرفاها أوب. حمن: اكتب استنتاجا عن الأشكال المتشابهة التي ليس من الضروري أن يكون لها القياس نفسه. تُسمي الأشكال التي لها الشكل نفسه، وليس بالضرورة أن يكون لها القياس نفسه أشكالا متشابهة. فالمثلث أب جـ أدناه يشابه المثلث س صع. وبالرموز الفصل : الهندسة: المضلعات أب جـ - 4 س صع. اسم اسم ۱۱۸ ۱۱۸ e م ١,٥ سم اسم الأضلاع المتقابلة، هي: آب و س ص ، أجـ وسع ، ب ج و صع وتُسمى هذه الأضلاع في الأشكال المتشابهة أضلاعًا متناظرة. الزوايا المتقابلة، هي: حب و خص. وتُسمى هذه الزوايا في الأشكال المتشابهة زوايا متناظرة. وزارة التعليم Ministry of Education 2024-1446

المستطيلات أدناه لهما الشكل نفسة ولكن بقياسات مختلفة وكذلك المثلثات انسخ الأشكال على ورقة منقطة ثم أوجد قياس كل زاوية باستعمال المنقلة وطول ضلع باستعمال المسطرة

معنى الأشكال المتشابهة

قراءة الرياضيات رموز هندسية القطعة المستقيمة التي طرفاها أ و ب

فكرة الدرس أحدد ما إذا كانت الأشكال متشابهة واجد الطول المجهول في شكلين متشابهين

الأشكال المتشابهة

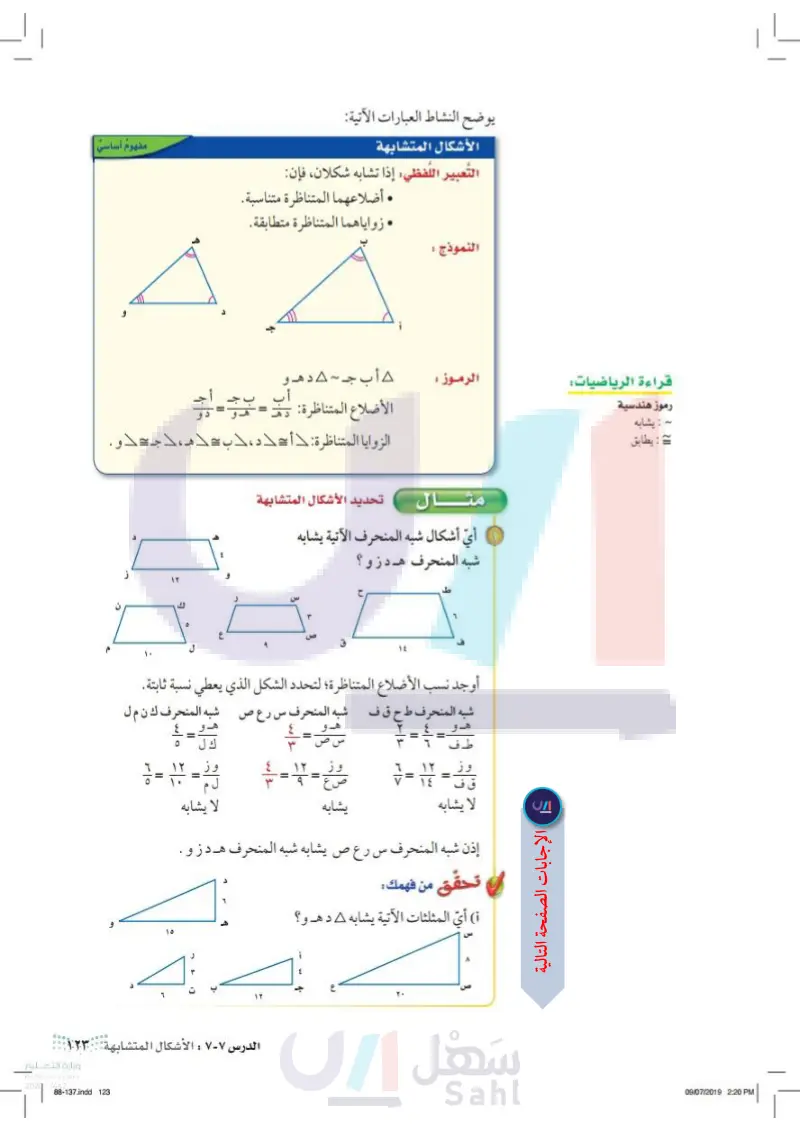
يوضح النشاط العبارات الآتية: الأشكال المتشابهة التعبير اللفظي: إذا تشابه شكلان، فإن النموذج : . أضلاعهما المتناظرة متناسبة. . زواياهما المتناظرة متطابقة. قراءة الرياضيات الرموز : أ ب جـ - ۵ دهـو أب رموز هندسية : يشابه = : يطابق مفهوم أساسي الأضلاع المتناظرة: دهـ = هـو = دو الزوايا المتناظرة أحد ، حب = لم ، جـ = دو تحديد الأشكال المتشابهة أي أشكال شبه المنحرف الآتية يشابه شبه المنحرف هـ دز و ؟ 14 1+ أوجد نسب الأضلاع المتناظرة؛ لتحدد الشكل الذي يعطي نسبة ثابتة. شبه المنحرف ط ح ق ف شبه المنحرف س رع ص شبه المنحرف ك ن م ل هـو س ص وز ۱۲ ۱۰ = = لا يشابه صع يشابه = لا يشابه إذن شبه المنحرف س رع ص يشابه شبه المنحرف هـ دز و . تحقق من فهمك : (أ) أي المثلثات الآتية يشابه د هـو ؟ IT 10 الدرس ۸-۷ : الأشكال المتشابهة الت٦٩ 2024-1446

الأشكال المتشابهة

ي أشكال شبه المنحرف الآتية يشابه شبه المنحرف هـ د ز و؟

أي المثلثات الآتية يشابه المثلث د ه و

قرأءة الرياضيات رموز هندسية يطابق يشابه

۷۰ الفصل : الهندسة: المضلعات إيجاد قياسات الأضلاع في المثلثات المتشابهة إذا كان ل م ن - خ ع س ص ، فأوجد س ص. بما أن المثلثين متشابهان فإن نسب الأضلاع المتناظرة متساوية. اكتب تناسبا لإيجاد س ص. اكتب التناسب ١٨م دام ٦م دم ا ما ا تمثل طول س ص ١٨ × ٤ = 11 ١٦ = ٧٢ أوجد ناتج الضرب التبادلي بسط أ = ١٢ تحقق من فهمك : اقسم كلا الطرفين على ٦ . س ص = ١٢ مترا . ب) إذا كان ٥ أب جـ ~ و هـد، فأوجد أج. ۲۸ سم ٣٥ سم 1 سم يستعمل القياس غير المباشر أشكالا متشابهة لإيجاد قياسات الأشياء التي يصعب قياسها مباشرة . مثال من واقع الحياة ينابيع : في الصورة ينبوع يتدفق منه الماء إلى ارتفاع ۱۸ م ، فيصنع . ظلا طوله ۱۳ م. ما ارتفاع شجرة قريبة منه تصنع ظلا طوله ۱۹ على افتراض أن المثلثين متشابهان؟ الشجرة الينبوع الارتفاع الظل ۱۳ × س = ۱۸×۱۹ ١٣ س = ٣٤٢ س = ٢٦٣ إذن طول الشجرة يساوي ٢٦٣م. تحقق. من فهمك : أوجد حاصل الضرب التبادلي سط اقسم كلا الطرفين على ١٣ جـ) صورة : يريد أحمد تصغير صورة بعداها ٤ سم × ٥ سم، بحيث تناسب موقعا في مجلة عرضه ۲ سم، فما طول الصورة المصغرة؟ اسم وزارة التعليم Ministry of Education 2024-1446

إذا كان المثلث ل م ن يطابق المثلث ع س ص فأوجد قيمة س ص

القياس الغير باشر

إذا كان المثلث أ ب ج يطابق المثلث و ه د فأوجد أ ج

يريد أحمد تصغير صورة بعداها 4 سم *5 سم بحيث تناسب موقعا في مجلة عرضة 2سم فما طول الصورة المصغرة

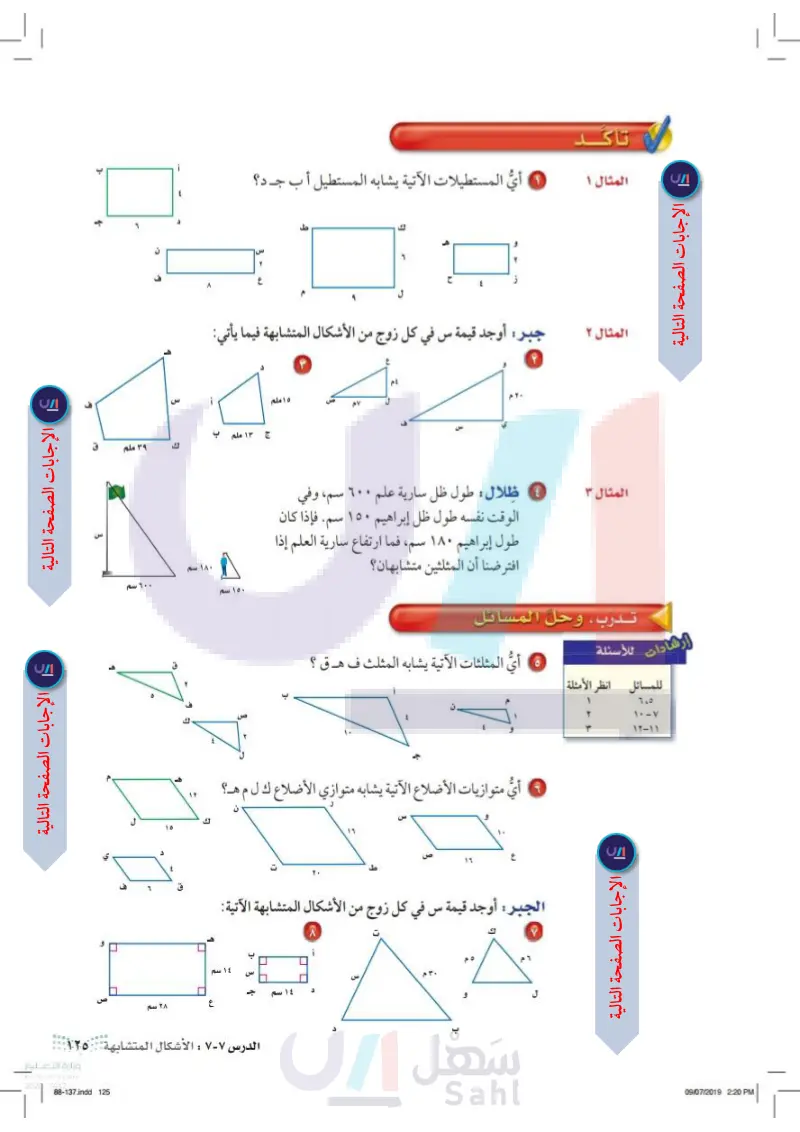
تاک المثال 1 المستطيلات الآتية يشابه المستطيل أ ب جـد؟ t ك المثال ٢ جبر أوجد قيمة س في كل زوج من الأشكال المتشابهة فيما يأتي: ١٥ ملم المثال ٣ ظلال طول ظل عمود الإنارة ٦٠٠ سم، وفي الوقت نفسه طول ظل إبراهيم ١٥٠ سم. فإذا كان طول إبراهيم ۱۸۰ سم، فما ارتفاع عمود الإنارة إذا افترضنا أن المثلثين متشابهان؟ تدرب، وحل المسائل ارشادات الأسئلة للمسائل انظر الأمثلة أي المثلثات الآتية يشابه المثلث ف هـ ق ؟ ٦،٥ ۱۰-۷ ۱۲-۱۱ 1 ج ١٣ ملم ب ٣٩ ملم ۱۸۰ سم ١٠٠ سم أي متوازيات الأضلاع الآتية يشابه متوازي الأضلاع ك ل م هـ؟ 19 الجبر أوجد قيمة س في كل زوج من الأشكال المتشابهة الآتية: ك ١٤ سم ١٤ سم 10 الدرس - : الأشكال المتشابهة ال٥٧١ 2024-1446

أي المستطيلات الآتية يشابه المستطيل أ ب ج د

جبر أوجد قيمة س في كل زوج من الأشكال المتشابهة فيما يأتي

ظلال طول ظل سارية علم 600سم وفي الوقت نفسه طول ظل إبراهيم 180 سم فما ارتفاع سارية العلم إذا افترضنا أن المثلثين متشابهان

الاشكال المتشابهة :أي المثلثات الآتية يشابه المثلث ف ه ق؟

أي متوازيات الأضلاع الآتية يشابه متوازي الأضلاع ك ل م ه؟

أوجد قيمة س في كل زوج من الأشكال المتشابهة الآتية

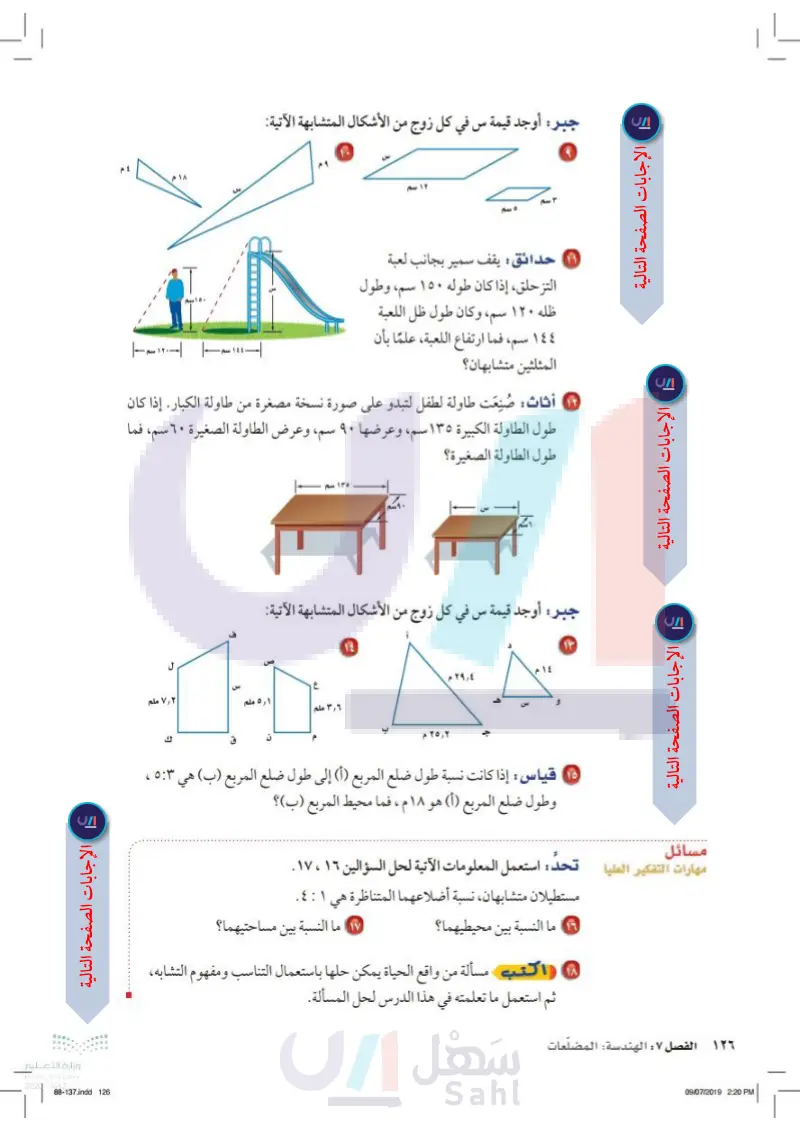
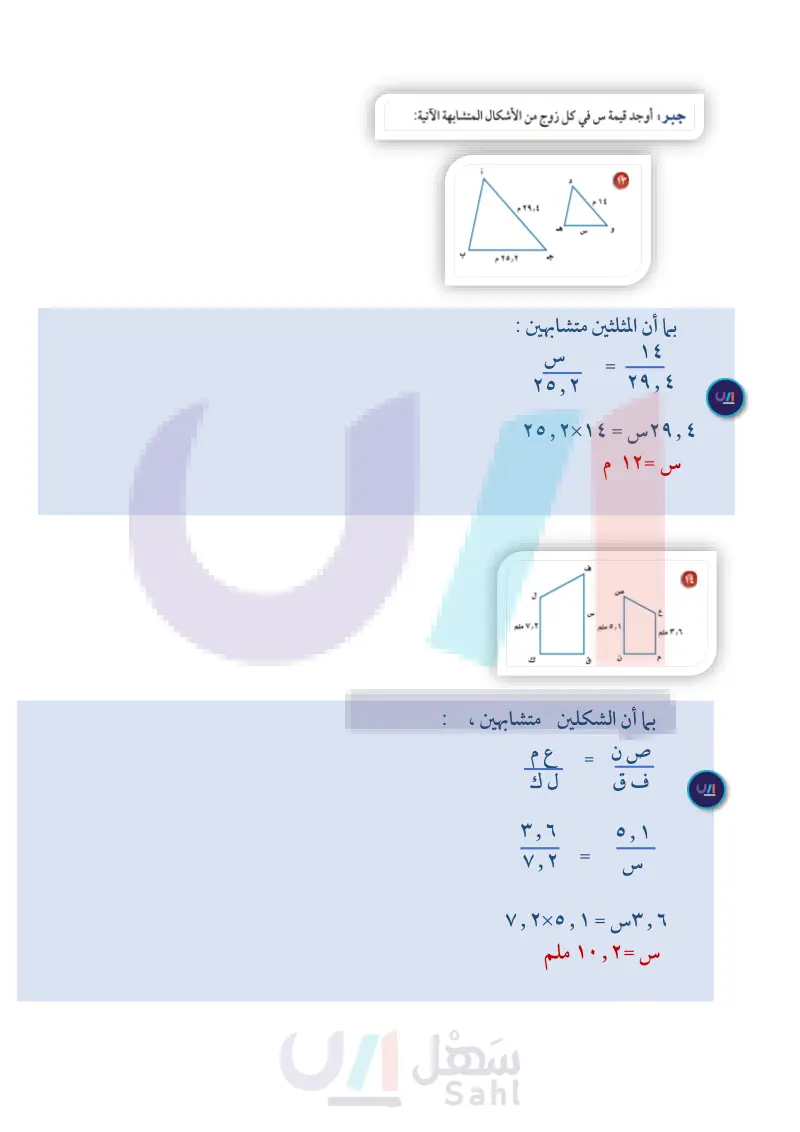
۷۲ جبر أوجد قيمة س في كل زوج من الأشكال المتشابهة الآتية: ١٢ سم حدائق : يقف سمير بجانب لعبة التزحلق، إذا كان طوله ١٥٠ سم، وطول ظله ١٢٠ سم، وكان طول ظل اللعبة ١٤٤ سم، فما ارتفاع اللعبة، علما بأن المثلثين متشابهان؟ سم | |-١٢٠ سم أثاث : صُنِعَت طاولة لطفل لتبدو على صورة نسخة مصغرة من طاولة الكبار. إذا كان طول الطاولة الكبيرة ١٣٥سم ، وعرضها ٩٠ سم وعرض الطاولة الصغيرة ٦٠سم، فما طول الطاولة الصغيرة؟ جبر: أوجد قيمة س في كل زوج من الأشكال المتشابهة الآتية: ٢٩,٤ م ٢٥,٢م ٥,١ ملم ٧,٢ ملم ٣,٦ ملم قياس : إذا كانت نسبة طول ضلع المربع (أ) إلى طول ضلع المربع (ب ) . وطول ضلع المربع (أ) هو ۱۸ م ، فما محيط المربع (ب)؟ مسائل تحد: مهارات التفكير العليا : استعمل المعلومات الآتية لحل السؤالين ١٦ ، ١٧ . مستطيلان متشابهان نسبة أضلاعهما المتناظرة . ما النسبة بين محيطيهما ؟ هي .: 1 ما النسبة بين مساحتيهما ؟ اكتب مسألة من واقع الحياة يمكن حلها باستعمال التناسب ومفهوم التشابه، ثم استعمل ما تعلمته في هذا الدرس لحل المسألة. الفصل : الهندسة: المضلعات وزارة التعليم Ministry of Education 2024-1446

جبر أوجد قيمة س في كل زوج من الشكال المتشابهة الآتية

حدائق يقف سمير بجانب لعبة التزحلق إذا كان طوله 150سم وكان طول ظل اللعبة 144سم فما ارتفاع اللعبة علما بأن المثلثين متشابهان

أثاث صنعت طاولة لطفل لتبدو على صورة نسخة مصغرة من طاولة الكبار إذا كان طول الطاولة الكبيرة 135 سم وعرضها 90 سم وعرض الطاولة الصغيرة 60 سم فما طول الطاولة الصغيرة

جبر13-14 أوجد قيمة س في كل زوج من الأشكال المتشابهة الآتية

إذا كانت نسبة طول ضلع المربع (أ) إلى طول ظلع المربع (ب) هي 5:3 وطول ضلع المربع (أ) هو 18 م فما محيط المربع (ب)

مستطيلان متشابهان نسبة أضلاعهما المتناظرة هي 1:4 ما النسبة بين محيطهما

اكتب مسألة من واقع الحياة يمكن حلها باستعمال التناسب ومفهوم التشابه ثم استعمل ما تعلمته في هذا الدرس لحل المسألة

تدريب على اختبار أي مستطيل مما يأتي يشابه المستطيل المجاور ؟ ۳م ٢ سم أي معادلة مما يأتي تنتج عند استعمال حاصل ۱۲ الضرب التبادلي؛ لحل التناسب = ؟؟ (i أ) ۱۲ × م = ١٥ ٦ م ب) ١٢×٦ = م × ١٥ ١٦ بوسة ب) بوصات جـ) ١٢× ١٥ = م ×٦ د) ١٢ + 6 = م : ١٥ ج) ۲۸سم دسم د) ١٢م جعة تراكمية هندسة صنّف الشكل الرباعي الآتي بأفضل اسم يصفه. (الدرس ٨ - ٦) L مثلث فيه زاويتان قياساهما ٤٤ ، ٦٧ . ما قياس الزاوية الثالثة ؟ (الدرس ٨-٤) الاستعداد للدرس اللاحق مهارة سابقة : حُلَّ كل معادلة مما يأتي: ه أ = ١٢٠ ٢٥ ٩٤٠ = ٨ن ٢٤ ٣٦٠ - ٤س ٦ ت = ۷۲۰ الدرس - : الأشكال المتشابهة الت٧٣ 2024-1446

أي مستطيل مما يأتي يشابه المستطيل المجاور

صنف الشكل الرباعي الآتي بأفضل اسم يصفه

حل كل معادلة مما يأتي 5أ=120

أي معادلة مما يأتي تنتج عند استعمال الضرب التبادلي لحل التناسب 12/15=م/6

مثلث فيه زاويتان قياسهما 44 درجة 67 درجة ما قياس الزاوية الثالثة