التكبير والتصغير - الرياضيات 1 - ثاني متوسط
الفصل1: الأعداد النسبية
الفصل2: الأعداد الحقيقية ونظرية فيثاغورس
الفصل3: التناسب والتشابه
نشاط الفصل1: الأعداد النسبية
نشاط الفصل2: الأعداد الحقيقية ونظرية فيثاغورس
رابط الدرس الرقمي www.ien.edu.sa التكبير والتصغير نشاط ۷-۳ فكرة الدرس أرسم صورة ناتجة عن تكبير شكل أو تصغيره. المفردات التمدد. مركز التمدد. التكبير. التصغير. يبين الشكل المجاور ورقة مربعات مقسمة إلى وحدات طول ضلع كل وحدة منها ٠,٥ سم، وبذلك تكون مساحة كل مربع تساوي ٠٠) سم . أعد رس (٥ سم". رسم , و الشكل على ورقة مربعات باستعمال مربعات أبعادها 1 سم 1x ۱ سم، استعمل النقطة أ نقطة بداية. قس الأطوال المتناظرة في الشكل الأصلي والشكل الجديد وقارن بينهما. صف العلاقة بين القياسين. كيف ترتبط هذه العلاقة بالتغيّر في أبعاد ورقة المربعات؟ خمّن : ما أبعاد ورقة المربعات التي يجب استعمالها لإنشاء نسخة جديدة من الشكل بحيث تكون أبعادها مساوية أربعة أمثال الأبعاد المناظرة لها في الشكل الأصلي؟ تسمى الصورة الناتجة عن تكبير شكل معطى أو تصغيره تمددًا. والصورة الناتجة عن التمدد تشبه الصورة الأصلية. وهذا يعني أن الأبعاد المتناظرة فيهما متناسبة. ويشير مركز التمدد إلى النقطة الثابتة التي تستعمل في القياس عند تعديل قياسات الشكل. وتسمى النسبة بين طول الصورة إلى طول الشكل الأصلي عامل مقياس التمدد. مثال رسم التمدد انسخ المضلع المرسوم جانبًا على ورقة مربعات، ثم ارسم صورة له باستعمال تمدد مركزه (أ) وعامل مقياسه ۲ . الخطوة ١ : ارسم أب (نصف المستقيم أب) بحيث يمتد إلى نهاية الورقة. د الخطوة ٢ : استعمل المسطرة في تعيين النقطة ب على أب بحيث يكون أبَ = ٢ (أب). الخطوة 3 : كرر الخطوتين (۱) و (۲) للنقاط جـ ، د ، ثم ارسم المضلع علمًا بأن أ = أَ . وزارة التعليم Ministry of Education 2024-1446 J. ما 11. \1 い ما الفصل :: التناسب والتشابه ١٣٤

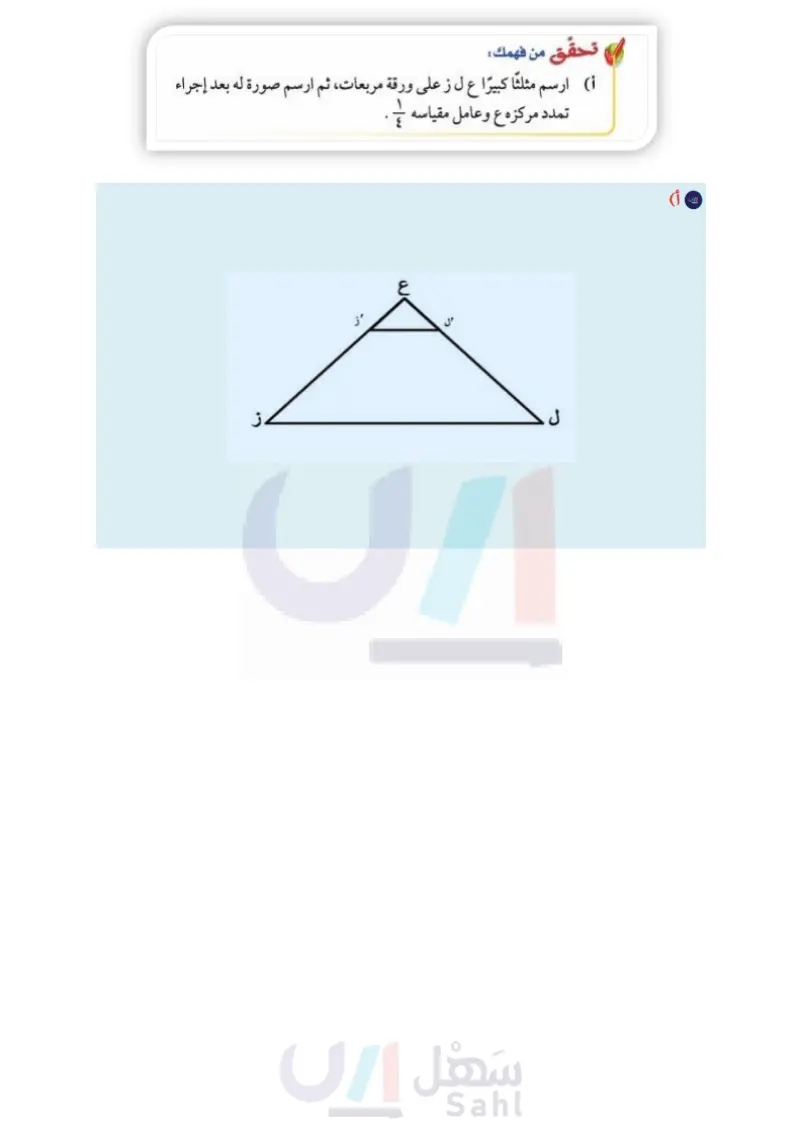
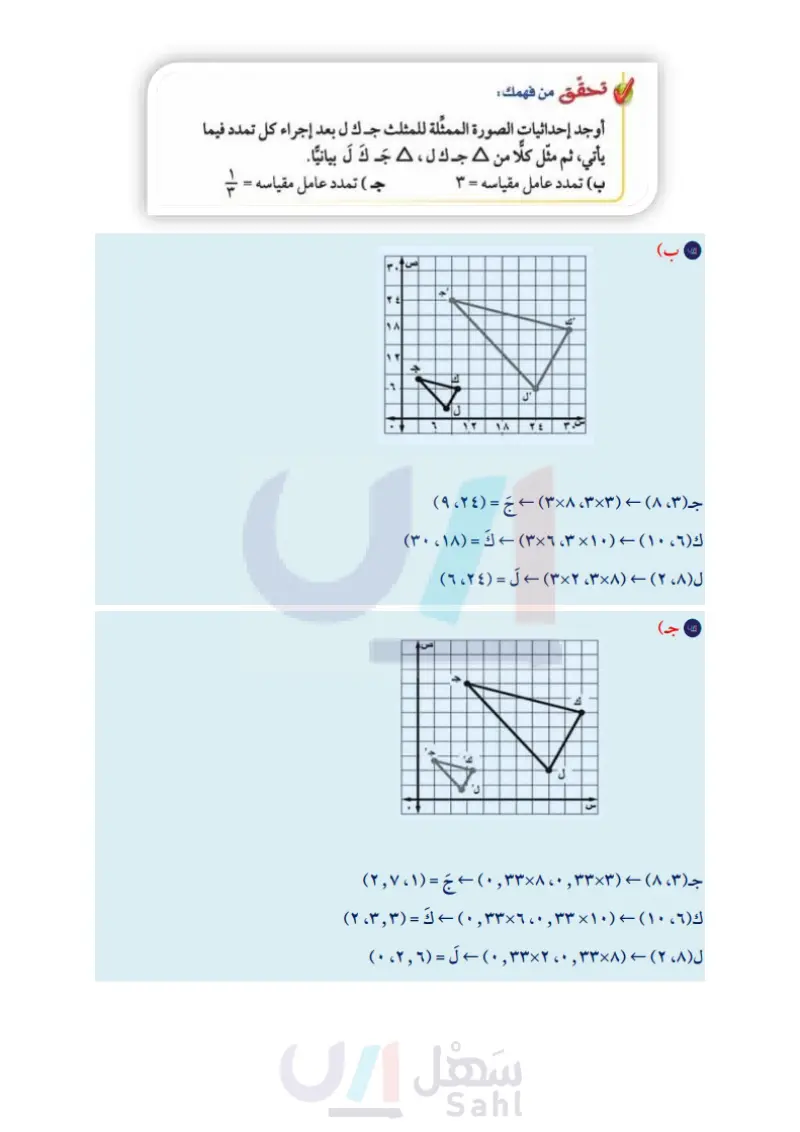
تحقق من فهمك : إرشادات للدراسة التمدد في المستوى الإحداثي النسبة بين الإحداثيات السينية والصادية لرؤوس الصورة إلى القيم المناظرة لها في الشكل الأصلي تساوي عامل مقياس التمدد. أ) ارسم م مثلثًا كبيرًا ع ل ز على ورقة مربعات ثم ارسم صورة له بعد إجراء تمدد مركزه ع وعامل مقياسه المثال (۱) ، إذا كانت إحداثيات النقطة أ . هي إحداثيات الإحداثيات الأصلية العلاقة الصورة دَ (٤ ، ٠) ج (٤،٤) ب (۲،۰) (٠،٠ ) فإن الجدول أدناه يبين إحداثيات النقاط د (۲، ۰) المتناظرة في الشكل الأصلي والصورة. لاحظ ج (۲، ۲) أن إحداثيات الصورة هي ( م س، م ص )، ب (۰، ۱) حيث م هي عامل المقياس. لإيجاد إحداثيات رؤوس الصورة بعد إجراء (...)1 (۲× (۲۰،۲×۲) ۲×۲) (۲×۱،۲۰) (۲۰،۲۰) (...) f تمدد مركزه (۰،۰) ، اضرب الإحداثيات السينية والصادية للنقاط في عامل المقياس. مثال التمثيل البياني للتمدد مثل بيانيًّا A جـ ك ل الذي رؤوسه جـ (۸،۳) ، ك (٦،١٠ ) ، ل (٨، ٢) ، ثم مثل بيانيًا الصورة التي تمثل جـكَ لَ الناتج عن تمدد عامل مقياسه يساوي + . لإيجاد الرؤوس بعد التمدد نضرب كل زوج في - على النحو الآتي : جـ (۸۳) - (۳× 勺 -(761.)5) ☑1 ☑ ) - كَ (٣،٥) P (V'↓) → (V × + ' 1 × †) → 5 (3*\) تا تحقق ارسم ثلاثة مستقيمات يمر كل منهم بنقطة الأصل، وبأحد رؤوس الشكل الأصلي. يجب أن تقع رؤوس الشكل بعد التمدد على المستقيمات نفسها. تحقق من فهمك : أوجد إحداثيات الصورة الممثلة للمثلث ج ك ل بعد إجراء كل تمدد فيما يأتي، ثم مثل كلًا من 4 ج ك ل ، ٥ جـ ك ل بيانيا. كَ ب تمدد عامل مقیاسه = ۳ جـ ) تمدد عامل مقياسه = + إذا تفحصت عامل المقياس والصور الناتجة عن التمدد في المثالين ١، ٢، يمكنك التوصل إلى ما يأتي: . التمدد الذي عامل مقياسه أكبر من ١ يؤدي إلى تكبير، حيث تكون الصورة أكبر من الشكل الأصلي. التمدد الذي يتراوح عامل مقياسه بين ٠ وَ ١ يؤدي إلى تصغير؛ حيث تكون الصورة أصغر من الشكل الأصلي. الدرس ٣ - ٧ : التكبير والتصغيرارة الت١٣٥يم - : Ministry of Education 2024-1446

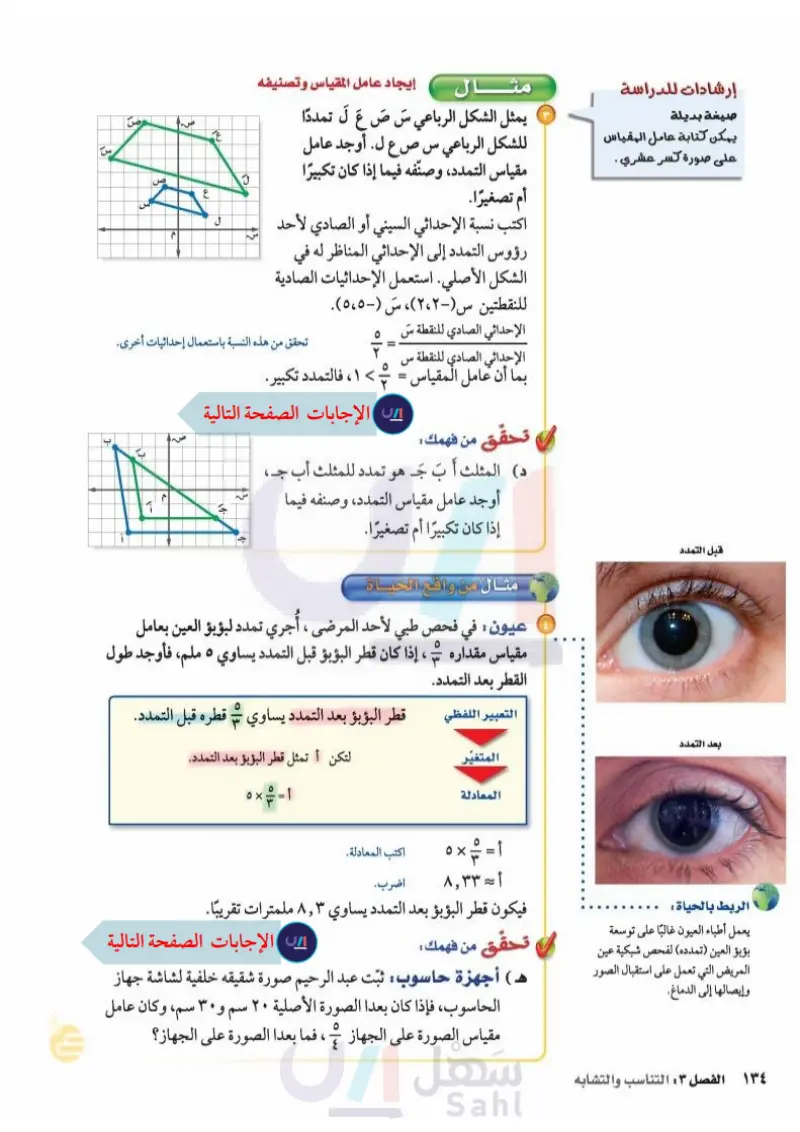
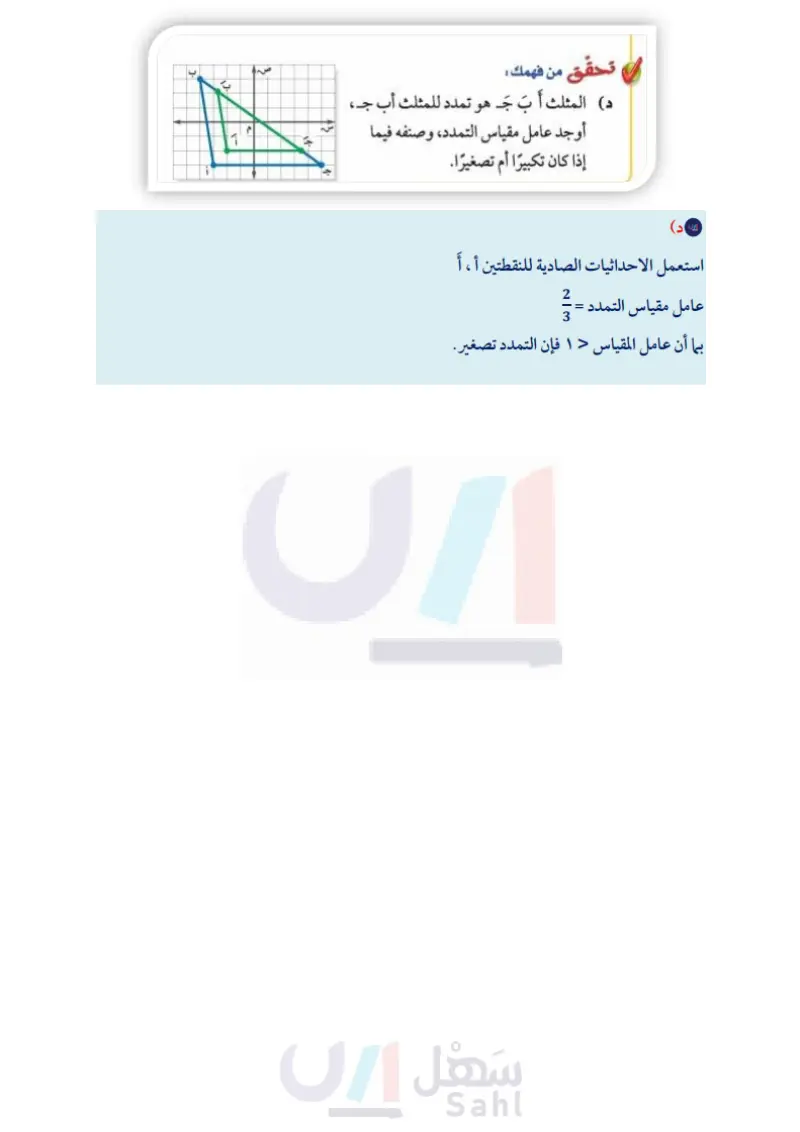
إرشادات للدراسة صيغة بديلة يمكن كتابة عامل المقياس على صورة كسر عشري . مثال إيجاد عامل المقياس وتصنيفه ٣ يمثل الشكل الرباعي سَ صَ عَ لَ تمددًا للشكل الرباعي س ص ع ل . أوجد عامل مقياس التمدد، وصنفه فيما إذا كان تكبيرًا أم تصغيرًا. اكتب نسبة الإحداثي السيني أو الصادي لأحد رؤوس التمدد إلى الإحداثي المناظر له في الشكل الأصلي. استعمل الإحداثيات الصادية للنقطتين س -٢،٢)، سَ (٥،٥). الإحداثي الصادي للنقطة سَ 11 قبل التمدد بعد التمدد الإحداثي الصادي للنقطة س ۲ 13 له ع س ل م تحقق من هذه النسبة باستعمال إحداثيات أخرى. بما أن عامل المقياس = - > ۱ ، فالتمدد تكبير . تحقق من فهمك : د) أت د المثلث أَ بَ جَـ هو تمدد للمثلث أب جـ، أوجد عامل مقياس التمدد، وصنفه فيما إذا كان تكبيرًا أم تصغيرًا. مثال من واقع الحياة : ، 13 ج ٦٠ عيون : في فحص طبي لأحد المرضى أُجري تمدد لبؤبؤ العين بعامل مقياس مقداره ، إذا كان قطر البؤبؤ قبل التمدد يساوي ٥ ملم، فأوجد طول القطر بعد التمدد. التعبير اللفظي قطر البؤبؤ بعد التمدد بساوي - قطره قبل التمدد. المتغير لتكن أ تمثل قطر البؤبؤ بعد التمدد. المعادلة 0 ☑ < = = 1 س الربط بالحياة : يعمل أطباء العيون غالبًا على توسعة أ = م × ٥ أ = ٨,٣٣ اكتب المعادلة. اضرب. فيكون قطر البؤبؤ بعد التمدد يساوي ٨٣ ملمترات تقريبًا. بؤبؤ العين (تمدده) لفحص شبكية عين تحقق من فهمك : المريض التي تعمل على استقبال الصور هـ ) أجهزة حاسوب: ثبت عبد الرحيم صورة شقيقه خلفية لشاشة جهاز وإيصالها إلى الدماغ. الحاسوب، فإذا كان بعدا الصورة الأصلية ۲۰سم و ٣٠ سم، وكان عامل مقياس الصورة على الجهاز ، فما بعدا الصورة على الجهاز؟ وزارة التعليم ١٣٦ الفصل :: التناسب والتشابه Ministry of Education 2024-1446

في فحص طبي لأحد المرضى أجري تمدد لبؤبؤ العين بعامل مقياس مقداره 5/3 إذا كان قطر البؤبؤ قبل التمدد يساوي ٥ ملم فأوجد طول القطر بعد التمدد

ثبت عبد الرحيم صورة شقيقه خلفية لشاشة جهاز سوب فإذا كان بعدا الصورة الأصلية ٢٠سم و ٣٠سم وكان عامل مقياس الصورة على الجهاز 5/4 فما بعدا الصورة على الجهاز؟


يعمل أطباء العيون غالبا على توسعة بؤبؤ العين
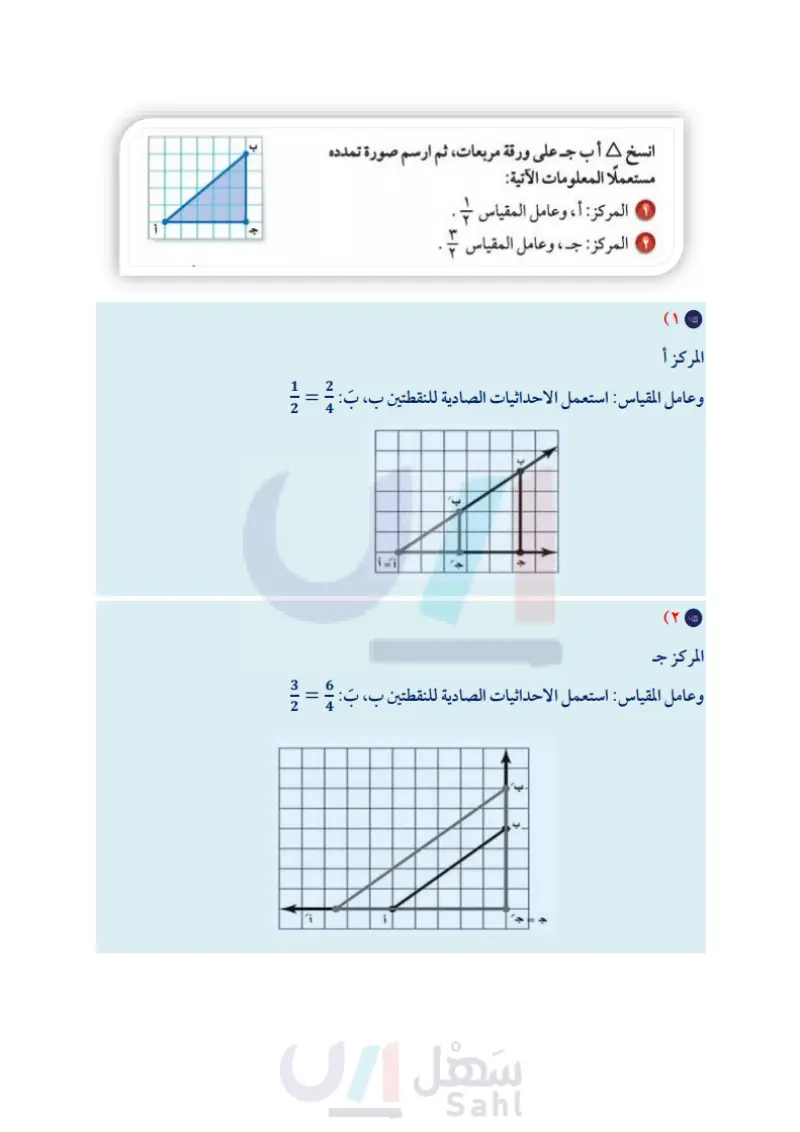
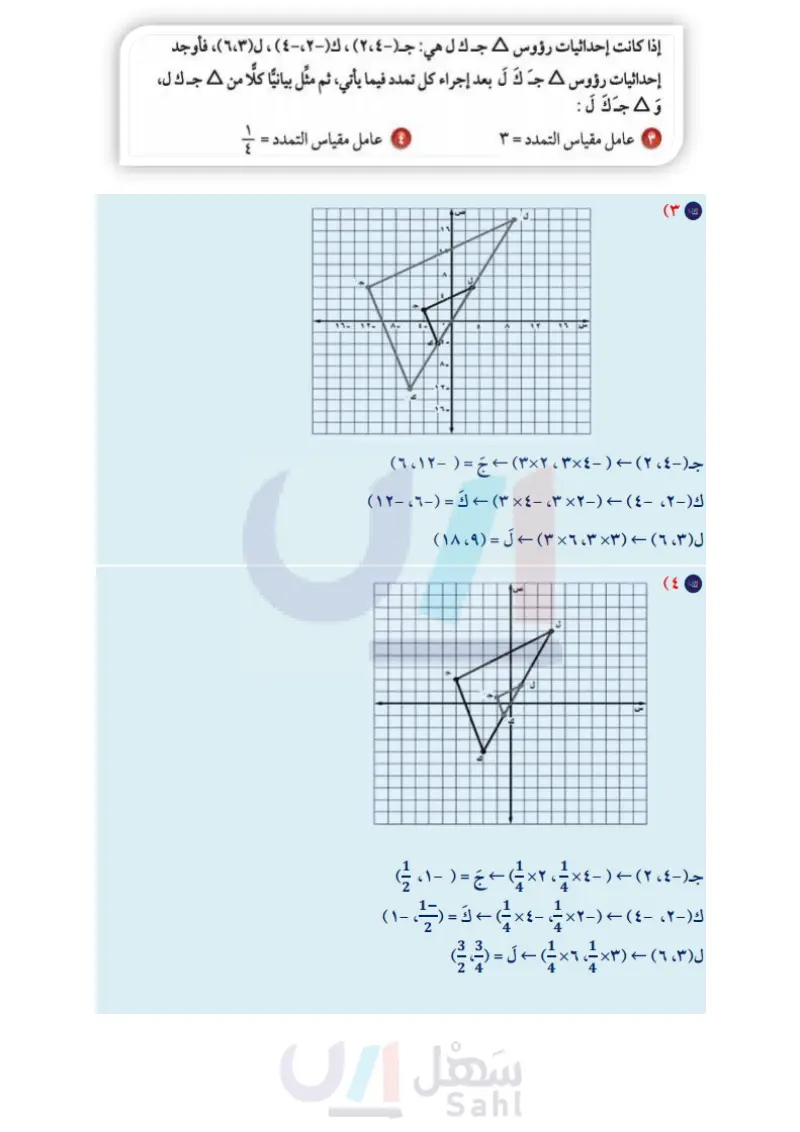
تأكد المثال ۱ انسخ 2 أب جـ على ورقة مربعات، ثم ارسم صورة تمدده مستعملا المعلومات الآتية: المركز : أ ، وعامل المقياس - . المركز : جـ ، وعامل المقياس - ງ المثال ٢ إذا كانت إحداثيات رؤوس A جـ ك ل هي: جـ (٢،٤) ، ك (-٤،٢ ) ، ل(٦،٣)، فأوجد . إحداثيات رؤوس A ج ك ل بعد إجراء كل تمدد فيما يأتي، ثم مثل بيانيا كلًا من A جـ ك ل، وَ جَكَ لَ : ۳ عامل مقياس التمدد = ٣ ٤ عامل مقياس التمدد = المثال ٣ في الشكل المجاور إذا كان أ ب تمددًا لـ آب، فأوجد عامل مقياس التمدد، وصنّفه فيما إذا كان تكبيرًا أو تصغيرًا. مخططا لمدرسته المثال ٤ 6 تصميم جرافيك : صمم عبد الرحمن بقياسات ١٥ سم في ١٩,٥سم. إذا رغب عبد الرحمن في تصغير المخطط باستعمال عامل مقياس ، فما أبعاد المخطط الجديد؟ } J. تدرب وحل المسائل إرشادات للأسئلة للأسئلة انظر الأمثلة انسخ كل شكل مما يأتي على ورقة مربعات ثم ارسم صورة تمدده مستعملا المعلومات الآتية: س م J. ع المركز : س، وعامل المقياس ۲ المركز: ع، وعامل المقياس . ل المركز : ل، وعامل المقياس ہے . المركز ن، وعامل المقياس ٢. أوجد إحداثيات رؤوس المضلع هـ جـكَ لَ الناتج عن تمدد المضلع هـ جـ ك ل باستعمال كل عامل مقياس فيما يأتي، ثم مثل بيانا المضلعين هـ جـ ك ل ، هَـجَـكَ لَ ١ هـ ( ٢،٠) ، جـ (۳، ۱ ) ، ك ، -٤ ) ، ل(-۲-۳)، وعامل المقياس = ٣. -6 ١ هـ - ٢،٦) ، جـ (٤، ٤ ) ، ك (٢،٧) ، ل ( ٢ - ٤ ) ، وعامل المقياس = -. - ٧ : التكبير والتصغيرارة التسليم الدرس 3 Ministry of Education 2024-1446 ۱۰ - ۷ ۱۲ - ۱۱ ١٣ - ١٦ ۱۷

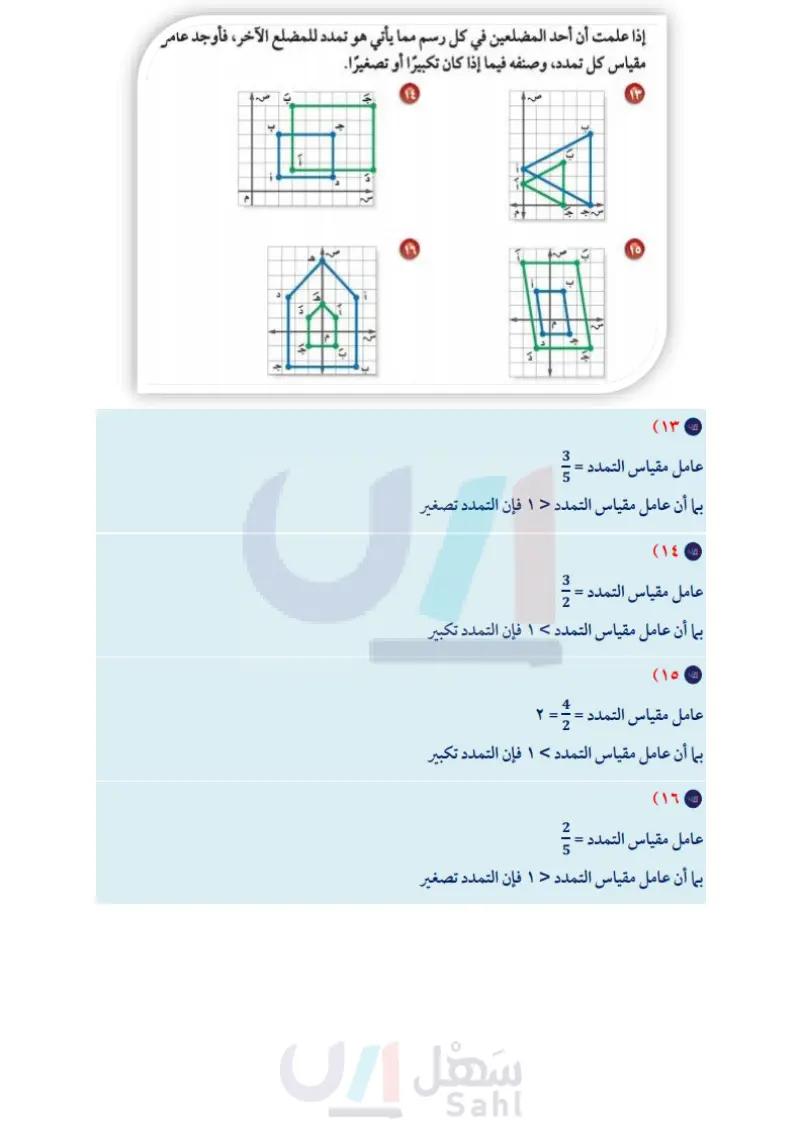
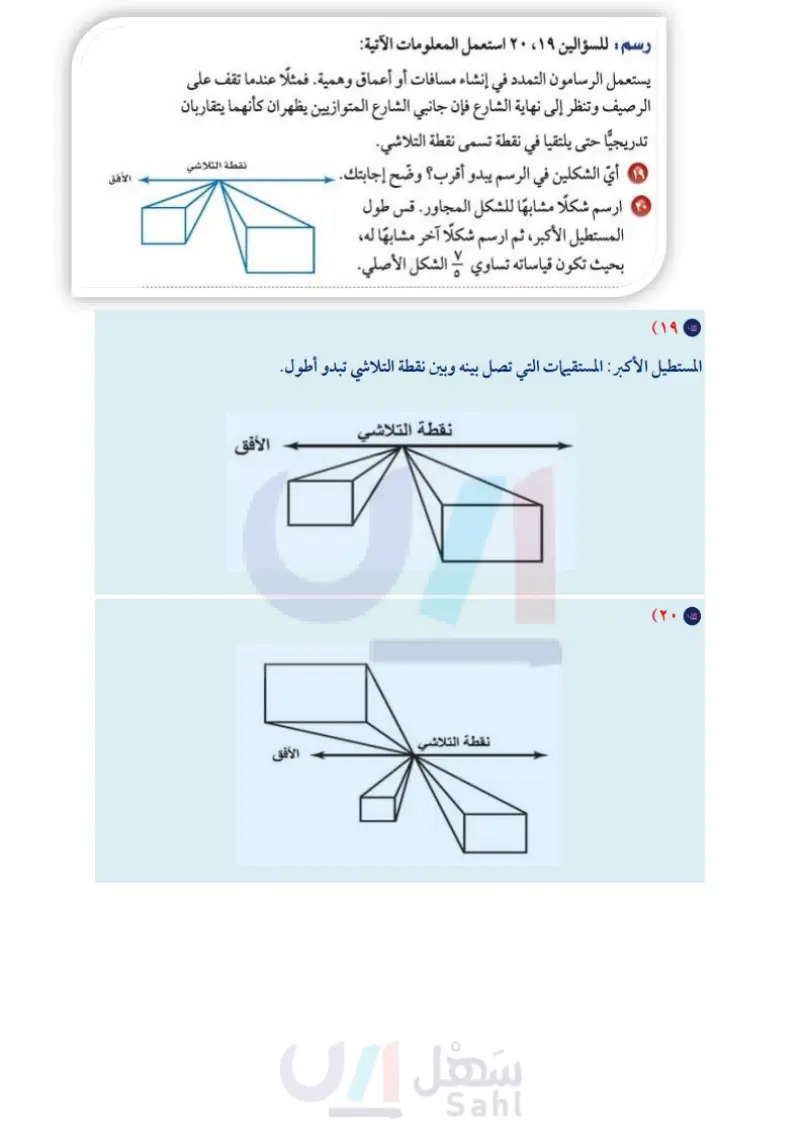
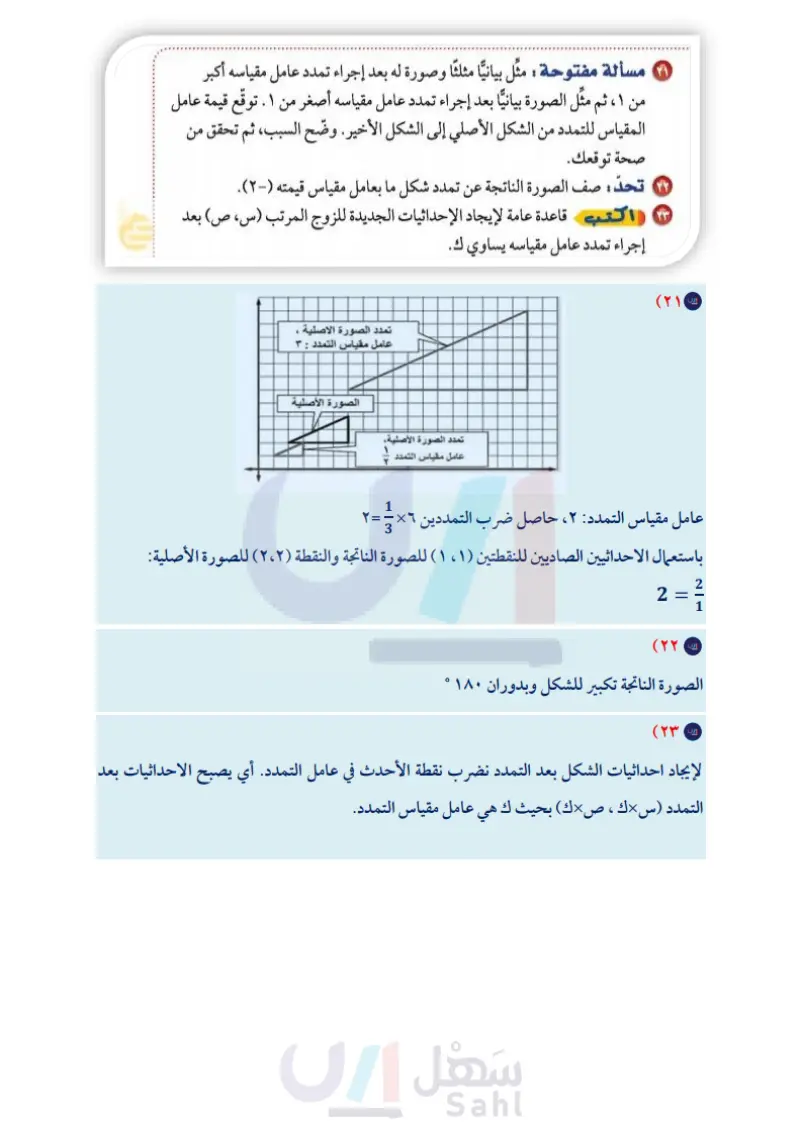
جا إذا علمت أن أحد المضلعين في كل رسم مما يأتي هو تمدد للمضلع الآخر، فأوجد عامل مقياس كل تمدد، وصنفه فيما إذا كان تكبيرًا أو تصغيرًا. J. 1 ١٤ い د ١٩٠ ١٦ \J. ١٩٠ 10 ٦٠ 12 ע د 17 11. 51. مسائل ۲ تصميم : لوضع صورة في مجلة ، يقوم المصمم بتصغير الصورة وفق عامل مقياس . ، فما أبعاد صورة وضعها المصمم إذا كان طولها الأصلي ١٥سم، وعرضها ۱۰ الأصلي ١٠سم؟ ١٥ جهاز العرض : يستعمل جهاز العرض في عرض الصور المرسومة على شفافيات على شاشة، بحيث تكون مكبرة وفق عامل مقياس يساوي ٣,٥. إذا كان طول الصورة الأصلية ٤ سم وعرضها ٣ سم، فما بعدا الصورة المعروضة على الشاشة؟ رسم: للسؤالين ،۱۹ ، ۲۰ استعمل المعلومات الآتية: نقطة التلاشي الأفق يستعمل الرسامون التمدد في إنشاء مسافات أو أعماق وهمية. فمثلا عندما تقف على الرصيف وتنظر إلى نهاية الشارع فإن جانبي الشارع المتوازيين يظهران كأنهما يتقاربان تدريجيا حتى يلتقيا في نقطة تسمى نقطة التلاشي. أيّ الشكلين في الرسم يبدو أقرب؟ وضح إجابتك . ارسم شكلًا مشابها للشكل المجاور. قس طول المستطيل الأكبر، ثم ارسم شكلا آخر مشابها له، بحيث تكون قياساته تساوي لا الشكل الأصلي. مسألة مفتوحة : مثَّل بيانيًا مثلثًا وصورة له بعد إجراء تمدد عامل مقياسه أكبر مهارات التفكير العليا من ١ ، ثم مثل الصورة بيانيًا بعد إجراء تمدد عامل مقياسه أصغر من ١. توقع قيمة عامل المقياس للتمدد من الشكل الأصلي إلى الشكل الأخير. وضح السبب، ثم تحقق من صحة توقعك. ۲ تحدّ : صف الصورة الناتجة عن تمدد شكل ما بعامل مقياس قيمته (۲). (اكتب قاعدة عامة لإيجاد الإحداثيات الجديدة للزوج المرتب (س، ص) بعد إجراء تمدد عامل مقياسه يساوي ك. وزافة التعليم Ministry of Education 2024-1446 الفصل :: التناسب والتشابه

لوضع صورة في مجلة يقوم المصمم بتصغير الصورة وفق عامل مقياس 3/10 فما أبعاد صورة وضعها المصمم إذا كان طولها الأصلي ١٥ سم وعرضها الأصلي 10سم


يستعمل جهاز العرض في عرض الصور المرسومة على شفافيات على شاشة بحيث تكون مكبرة وفق عامل مقياس يساوي ٣,٥ إذا كان طول الصورة الأصلية ٤ سم وعرضها ٣ سم فما بعدا الصورة المعروضة على الشاشة؟


م تدريب على اختبار في الشكل أدناه، إذا كان المربع س يشابه يمثل الشكل الرباعي أ ب ج د تمددًا للشكل المربع ص: الرباعي س ص ع ل : ۲۱ ٣٥ س ع اله س فأوجد عامل المقياس المستعمل لتمدد المربع سر إلى المربع ص. −|> 3|0 جـ) 이로 د) ۷ أيّ الأعداد التالية يمثل أفضل عامل مقياس تمدد استعمل لتحويل الشكل الرباعي أ ب جـد إلى الشكل الرباعي س ص ع ل ؟ (i -| -|2 جـ) ۲ د) ٣ مراجعة تراكمية (۲۷ المثلثان في الشكل المجاور متشابهان. اكتب تناسبًا وحُلَّه لإيجاد القياس الناقص ؟ (الدرس ٣ - ٦) اسم ب سم سم ٤,٥سم هندسة : مستطيل طوله ۱۲م وعرضه ۷م ما طول قطره مقربًا إلى أقرب جزء من عشرة؟ (الدرس ٢ - ٦) تكنولوجيا : تستعمل شهد جهاز GPS (نظام تحديد المواقع العالمي)؛ لتحديد المسافة المتبقية للوصول إلى المجمع التجاري. إذا كان موقعها الحالي على شاشة الجهاز المجاورة عند النقطة الحمراء، والمجمع التجاري عند النقطة الزرقاء، فكم المسافة المتبقية حتى تصل شهد إلى المجمع التجاري؟ (الدرس ٢ - ٦) کلم الاستعداد للدرس اللاحق مهارة سابقة : اكتب تناسبًا وحلّه بإيجاد قيمة س في كل مما يأتي: (الدرس ٣ - ٤) ٣ سم إلى ٥ أقدام مثل س سم إلى 4 أقدام ٤ بوصات إلى ٥ أميال مثل ٥ بوصات إلى س ميلًا. - ٧ : التكبير والتصغيرارة الت٣٩ليم الدرس 3 Ministry of Education 2024-1446



 0
0 

 0
0 

 1
1 

 0
0