إثبات توازي مستقيمين - الرياضيات 1-1 - أول ثانوي

رابط الدرس www.ien.edu.sa إثبات توازي مستقيمين Proving Lines Parallel 2-3 فيما سبق: درست استعمال خصائص المستقيمات المتوازية لماذا؟ عندما تنظر إلى سكة القطار، تجد أن البعد بين خطيها ثابت دائمًا حتى عند المنحنيات لتحديد الزوايا المتطابقة. والمنعطفات. فقد صممت السكك بدقة، بحيث الدرس (2-2) والآن : أميز المستقيمات المتوازية بناءً على علاقات بين أزواج من الزوايا الناتجة عن مستقيم قاطع. أبرهن توازي مستقيمين باستعمال العلاقات بين أزواج الزوايا. يكون خطاها متوازيين عند جميع النقاط ليسير عليها القطار بأمان. تحديد المستقيمين المتوازيين: خطا سكة القطار متوازيان، وكذلك الخطوط العرضية جميع في السكة متوازية أيضًا، والزوايا المتكوّنة بين خطّي السكة والخطوط العرضية للسكة المتوازية متناظرة. درست سابقا أن الزوايا المتناظرة تكون متطابقة عندما يكون المستقيمان متوازيين وعكس هذه العلاقة صحيح أيضًا. مسلمة 2.2 عكس مسلّمة الزاويتين المتناظرتين إذا قطع قاطع مستقيمين في مستوى، ونتج عن التقاطع زاويتان متناظرتان متطابقتان، فإن المستقيمين متوازيان أمثلة: إذا كانت 8 = 6 أو 27 = 25 أو 24 = 2 أو 23 = 1، 6 a أضف إلى مطويتك 1 2 4 3 7 6 5 . فإن a || b يمكنك استعمال عكس مسلّمة الزاويتين المتناظرتين لرسم مستقيمين متوازيين. إنشاءات هندسية رسم مستقيم مواز لمستقيم معلوم ويمر بنقطة لا تقع عليه الخطوة 1 : استعمل مسطرة AB، وعيّن نقطة C لا تقع على AB، وارسم CA . لرسم بما أن LECD = CAB من الخطوة 2: استعمل فرجارًا لنقل CAB ، بحيث تكون النقطة الخطوة 3 : ارسم CD . C رأس الزاوية الجديدة، وذلك من خلال الخطوات الآتية: ضع رأس الفرجار عند النقطة A ، وارسم قوسين يقطعان AC AB و في النقطتين . , • بفتحة الفرجار نفسها، ارسم قوسًا مركزه C يقطع AC . النقطة E • ارجع للنقطة M وافتح الفرجار بنفس طول MN. الإنشاء، وهما متناظرتان فإن AB || CD في • بفتحة الفرجار نفسها، ارسم قوسًا مركزه E، ويقطع القوس السابق في D كما في الشكل. وزارة التعليم Ministry of Education 2024-1446 E D M B A N M. E B A B A الفصل 2 التوازي والتعامد 102

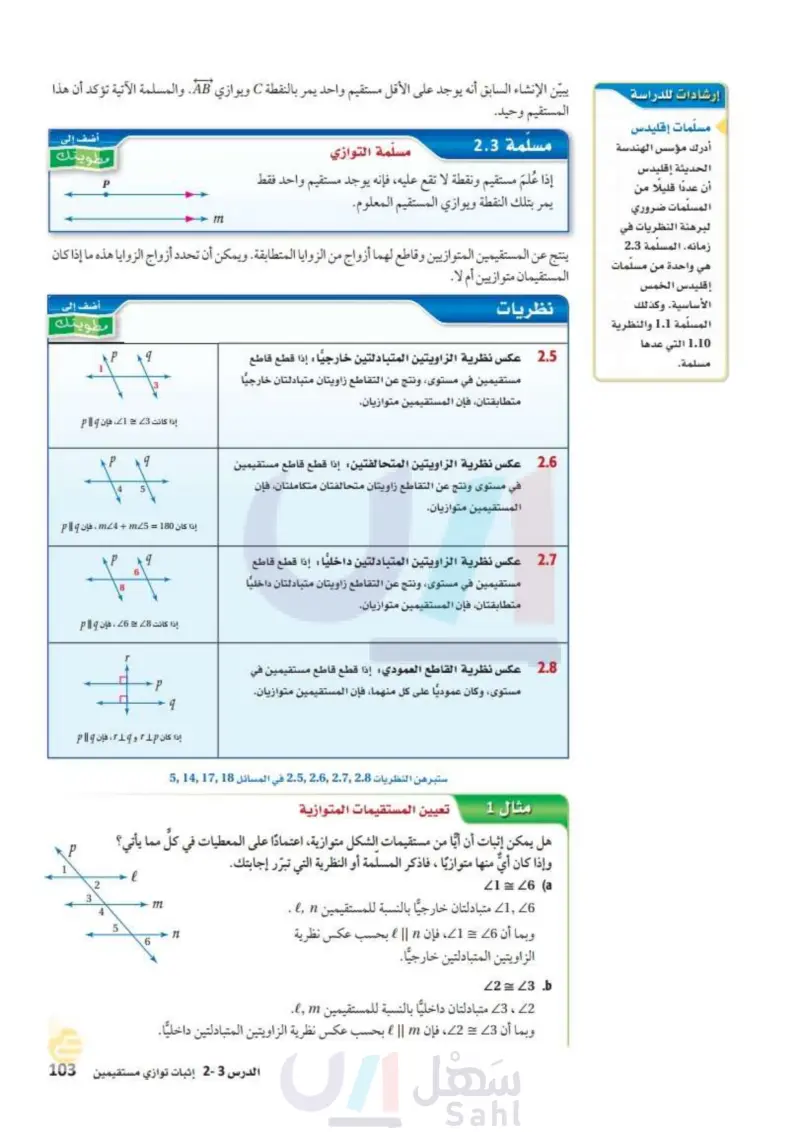
إرشادات للدراسة مسلّمات إقليدس أدرك مؤسس الهندسة الحديثة إقليدس أن عددا قليلا من المسلمات ضروري لبرهنة النظريات في زمانه. المسلمة 2.3 هي واحدة من مسلّمات إقليدس الخمس الأساسية. وكذلك المسلمة 1.1 والنظرية 1.10 التي عدها مسلمة. يبين الإنشاء السابق أنه يوجد على الأقل مستقيم واحد يمر بالنقطة C ويوازي .AB. والمسلمة الآتية تؤكد أن هذا المستقيم وحيد. مسلمة 2.3 مسلمة التوازي إذا عُلمَ مستقيم ونقطة لا تقع عليه، فإنه يوجد مستقيم واحد فقط يمر بتلك النقطة ويوازي المستقيم المعلوم. m أضف إلى مطويتك P ينتج عن المستقيمين المتوازيين وقاطع لهما أزواج من الزوايا المتطابقة. ويمكن أن تحدد أزواج الزوايا هذه ما إذا كان أضف إلى مطويتك المستقيمان متوازيين أم لا. نظريات 2.5 عكس نظرية الزاويتين المتبادلتين خارجيا : إذا قطع قاطع مستقيمين في مستوى ، ونتج عن التقاطع زاويتان متبادلتان خارجيًا متطابقتان، فإن المستقيمين متوازيان. 3 P q إذا كانت 23 = 1، فإن p || q P q 4 عكس نظرية الزاويتين المتحالفتين : إذا قطع قاطع مستقيمين في مستوى ونتج عن التقاطع زاويتان متحالفتان متكاملتان، فإن المستقيمين متوازيان عكس نظرية الزاويتين المتبادلتين داخليا : إذا قطع قاطع مستقيمين في مستوى، ونتج عن التقاطع زاويتان متبادلتان داخليا متطابقتان، فإن المستقيمين متوازيان. إذا كان 180 = m4 + m25 ، فإن p || q P 8 6 q إذا كانت 28 = 26 ، فإن p || q p -P q عکس نظرية القاطع العمودي : إذا قطع قاطع مستقيمين في مستوى، وكان عموديًا على كل منهما، فإن المستقيمين متوازيان. إذا كان 11p و 19 ، فإن p || q ستبرهن النظريات 25 في المسائل 1347 مثال 1 تعيين المستقيمات المتوازية 2.6 2.7 2.8 هل يمكن إثبات أن أيا من مستقيمات الشكل متوازية، اعتمادًا على المعطيات في كل مما يأتي؟ وإذا كان أي منها متوازيًا ، فاذكر المسلمة أو النظرية التي تبرّر إجابتك. P l 3 m 5 ➤n 6 21 = 26 (a Z6 16 متبادلتان خارجيًا بالنسبة للمستقيمين . , وبما أن 6 = 1 ، فإن n || بحسب عكس نظرية الزاويتين المتبادلتين خارجيًا. 22 = 23 .b 2 ، 3 متبادلتان داخليًا بالنسبة للمستقيمين . و وبما أن 2،3، فإن m || بحسب عكس نظرية الزاويتين المتبادلتين داخليا. الدرس - إثبات توازي مستقيمين ال103م Ministry of Education 2024-1446

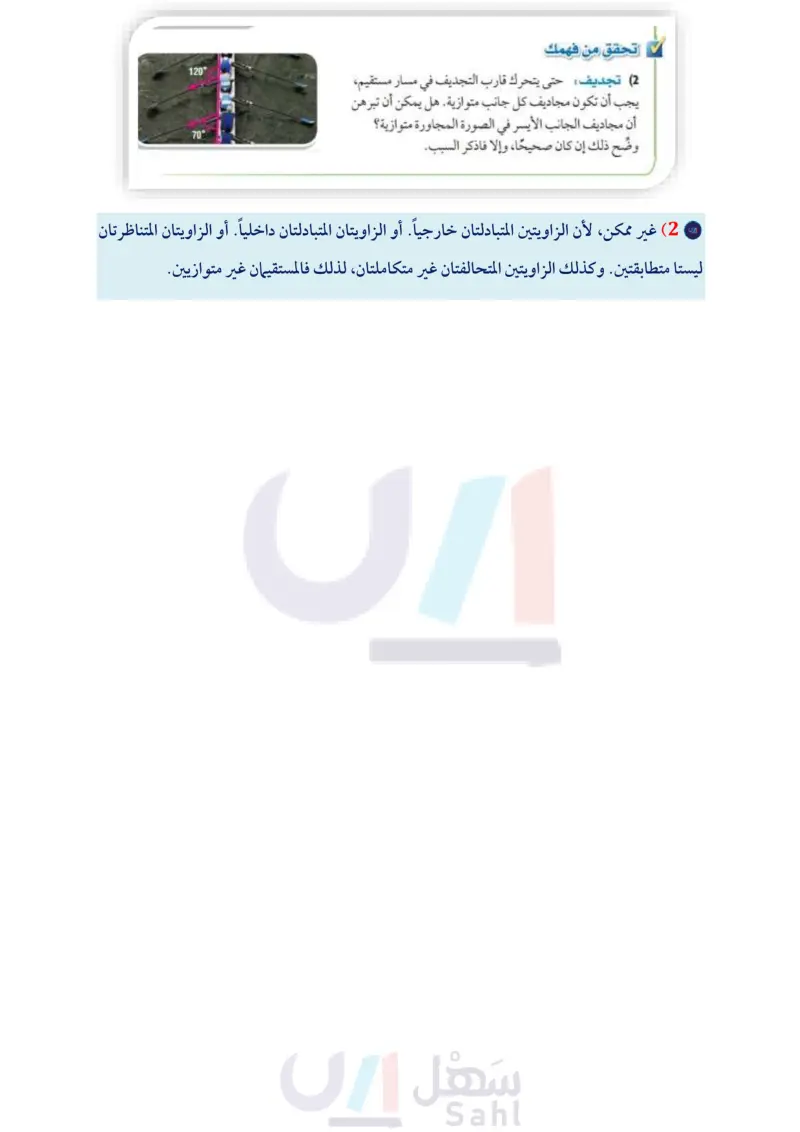
a 6 تحقق من فهمك 12 56 43 l 23 = 11 (18) 87 9 10 13 14 21 = 215 (10 22 = 28 (1A 212 = 214 (1 12/11 16 15 m Z8Z6 (1F mZ8+mZ13 = 180° (1E إرشادات للدراسة إثبات توازي مستقيمين عندما يقطع قاطع مستقيمين متوازيين إما أن تكون أزواج الزوايا الناتجة متطابقة أو متكاملة. وإذا نتج عن مستقيمين وقاطع لهما زوايا لا تحقق هذا الشرط، فلا يمكن أن يكون المستقيمان متوازيين إثبات توازي مستقيمين: يمكن استعمال العلاقة بين أزواج الزوايا الناتجة عن مستقيمين وقاطع لهما لإثبات أن المستقيمين متوازيان. مثال 2 من واقع الحياة إثبات توازي مستقيمين سلالم کل درجة من درجات السلّم في الشكل المجاور عمودية على دعامتيه الرئيستين، هل يمكن إثبات أن الدعامتين الرئيستين متوازيتان، وأن جميع الدرجات متوازية؟ وضّح ذلك إن كان صحيحًا، وإلا فاذكر السبب. بما أن الدعامتين الرئيستين عموديتان على كل درجة فهما متوازيتان بحسب عكس نظرية القاطع العمودي. وبما أن أي درجتين في السلم عموديتان على كل من الدعامتين الرئيستين فهما متوازيتان أيضًا. تحقق من فهمك (2) تجديف حتى يتحرك قارب التجديف في مسار مستقيم، يجب أن تكون مجاديف كل جانب متوازية. هل يمكن أن تبرهن أن مجاديف الجانب الأيسر في الصورة المجاورة متوازية؟ وضّح ذلك إن كان صحيحًا، وإلا فاذكر السبب. 120° 70° 1/2 j 3 k # 9 ہلے 4 7 5 10 8 6 l m وزارة التعليم Ministry of Education 2024-1446 تأكد المثال 1 هل يمكن إثبات أن أيا من مستقيمات الشكل متوازية، اعتمادًا على المعطيات في كل مما يأتي؟ وإذا كان أيها متوازيًا ، فاذكر المسلمة أو النظرية التي تبرّر إجابتك. 1 l 3 m 2 22 = 25 2 21 = 23 (1 mZ6+ mZ8 = 180° (4 23 = 210 (3) المثال 2 (5 برهان أكمل برهان النظرية 2.5 . (5) المعطيات: 22 = 1 المطلوب : e || m العبارات المبررات a معطى خاصية التعدي للتطابق (b البرهان : 21 = 22 (a Z2 Z3 (b Z123 (c (d e || m (d الفصل 2 التوازي والتعامد 104

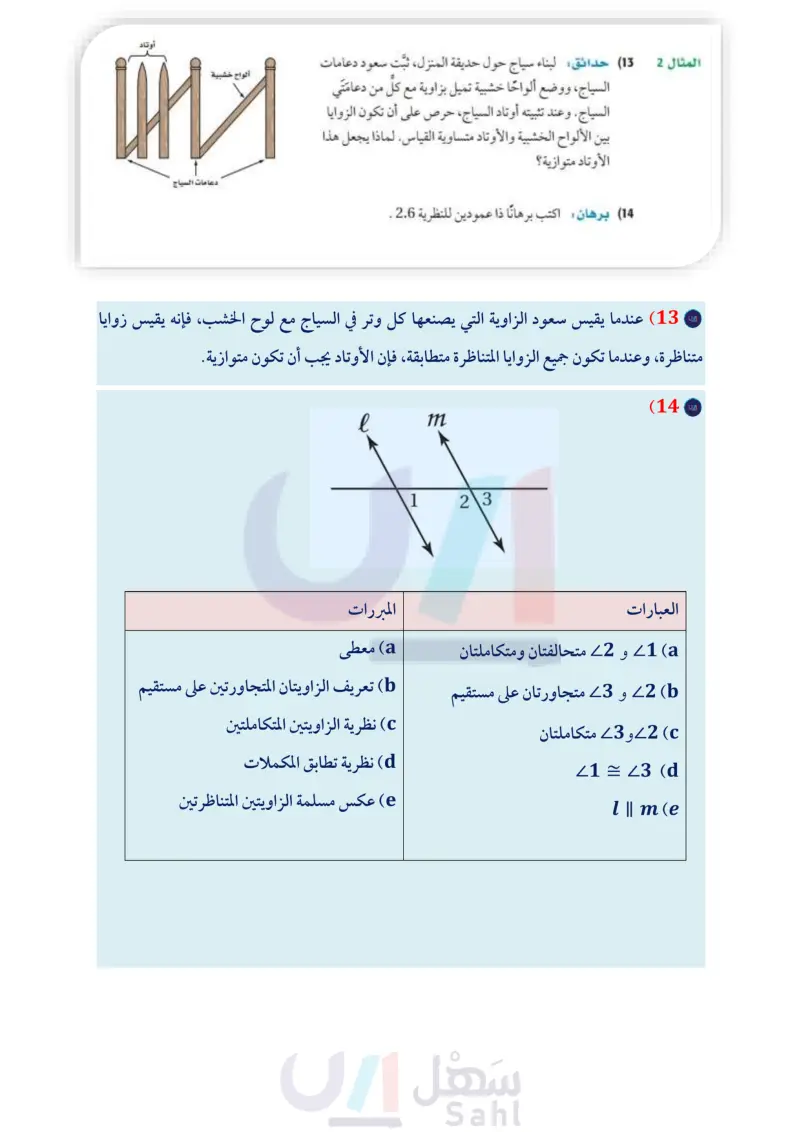
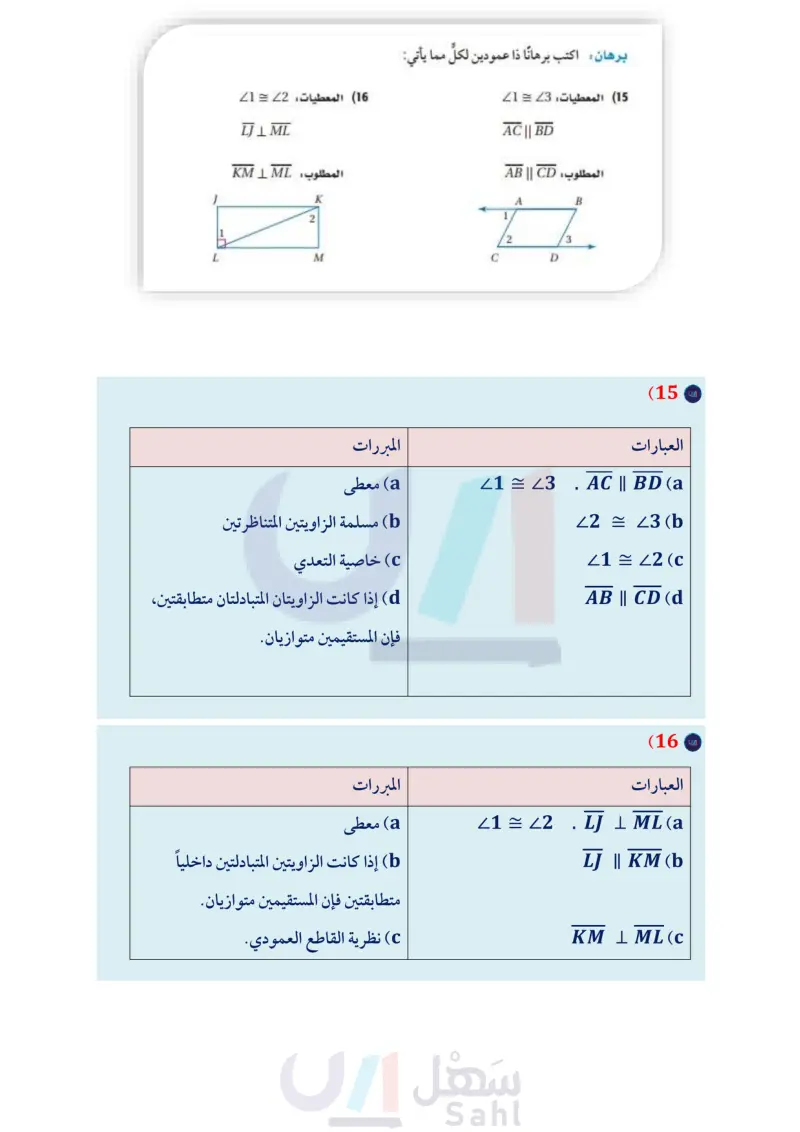
135° 1 له 2 135° 3 4 56 7 89 ح (6) كراسي هل يمكن إثبات أن مسند الظهر ومسند القدمين لكرسي الاسترخاء في الشكل المجاور متوازيان؟ وضح ذلك إذا كان صحيحا، وإلا فاذكر السبب. تدرب وحل المسائل المثال 1 هل يمكن إثبات أن أيا من مستقيمات الشكل متوازية، اعتمادًا على المعطيات في كل مما يأتي ؟ وإذا كان أيّها متوازيًا ، فاذكر المسلمة أو النظرية التي تبرّر إجابتك. 22 = 29 (8 21 = 22 (7 mZ3+mZ6 = 180° (10 mZ7 + mZ8 = 180° (9 Z4Z5 (12 23 = 27 (11 المثال 2 (13) حدائق : لبناء سياج حول حديقة المنزل، ثبت سعود دعامات السياج، ووضع ألواحًا خشبية تميل بزاوية مع كل من دعامتي السياج. وعند تثبيته أوتاد السياج حرص على أن تكون الزوايا بين الألواح الخشبية والأوتاد متساوية القياس. لماذا يجعل هذا الأوتاد متوازية ؟ (14) برهان اكتب برهانا ذا عمودين للنظرية 2.6 . برهان اكتب برهانا ذا عمودين لكلِّ مما يأتي: (15) المعطيات: 23 = 1 (16) المعطيات: 2 = 1 ألواح خشبية دعامات السياج أوتاد J LJ ML المطلوب : KM I ML K 2 L M 18) النظرية 2.8 الدرس 3-2- إثبات توازي مستقيمين ال105م Ministry of Education 2024-1446 AC || BD المطلوب : AB || CD A 1 3 C D B برهان اكتب برهانًا حرا لكلّ من النظريتين الآتيتين: 17) النظرية 2.7

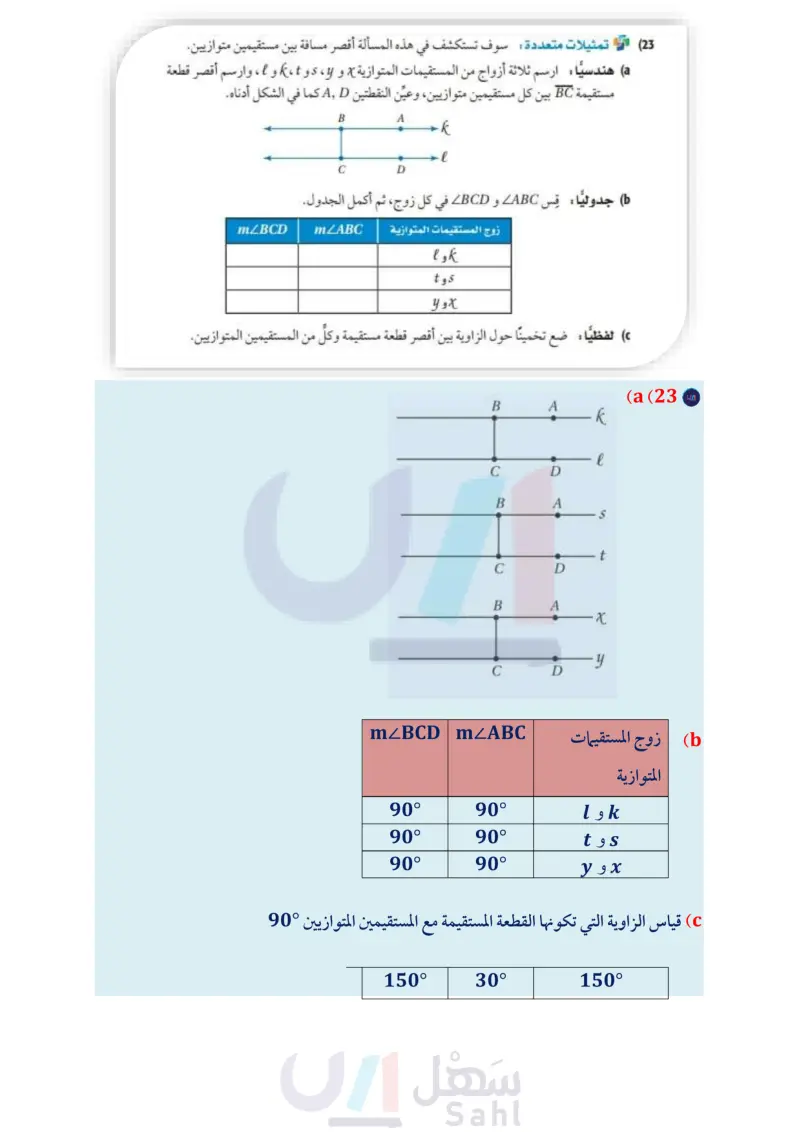
S m n 92° 19 درج ما العلاقة بين حواف أسطح الدرجات في الشكل المجاور؟ برر إجابتك. حدد ما إذا كان المستقيمان 5, متوازيين أم لا في كل مما يأتي. برّر إجابتك. (22 65° 27° T S 57 41° 23° 75° (21 32° 32° 64° (20 (23) تمثيلات متعددة : سوف تستكشف في هذه المسألة أقصر مسافة بين مستقيمين متوازيين. : 6 S t 6 (a) هندسيا : ارسم ثلاثة أزواج من المستقيمات المتوازية x و y ، و ،K و e ، وارسم أقصر قطعة مستقيمة BC بين كل مستقيمين متوازيين وعيّن النقطتين A كما في الشكل أدناه. mZBCD B A -k l C D جدوليا : قس ABC و BCD في كل زوج، ثم أكمل الجدول. mZABC زوج المستقيمات المتوازية K و L s وt X و Y لفظيا : ضع تخمينا حول الزاوية بين أقصر قطعة مستقيمة وكلُّ من المستقيمين المتوازيين. W X 1 مسائل مهارات التفكير العليا (24) اكتشف الخطأ يحاول كل من سامي ومنصور تحديد المستقيمات المتوازية في الشكل المجاور. فقال سامي: بما أن 2 = 1 ، إذن WY || XZ. أما منصور فلم يوافقه وقال: بما أن 22 = 21 ، إذن WX || YZ. أي منهما على صواب؟ وضح إجابتك. N له (25) تبرير هل تبقى النظرية 2.8 صحيحة إذا كان المستقيمان لا يقعان في المستوى نفسه؟ ارسم شكلًا يبرر إجابتك. 26 مسألة مفتوحة: ارسم المثلث ABC أنشئ مستقيمًا يوازي BC بالنقطة A. ويمر استعمل القياس؛ لتتحقق من أن المستقيم الذي رسمته يوازي BC Y وزارة التعليم Ministry of Education 2024-1446 ( أثبت صحة الإنشاء رياضيا. الفصل 2 التوازي والتعامد 106

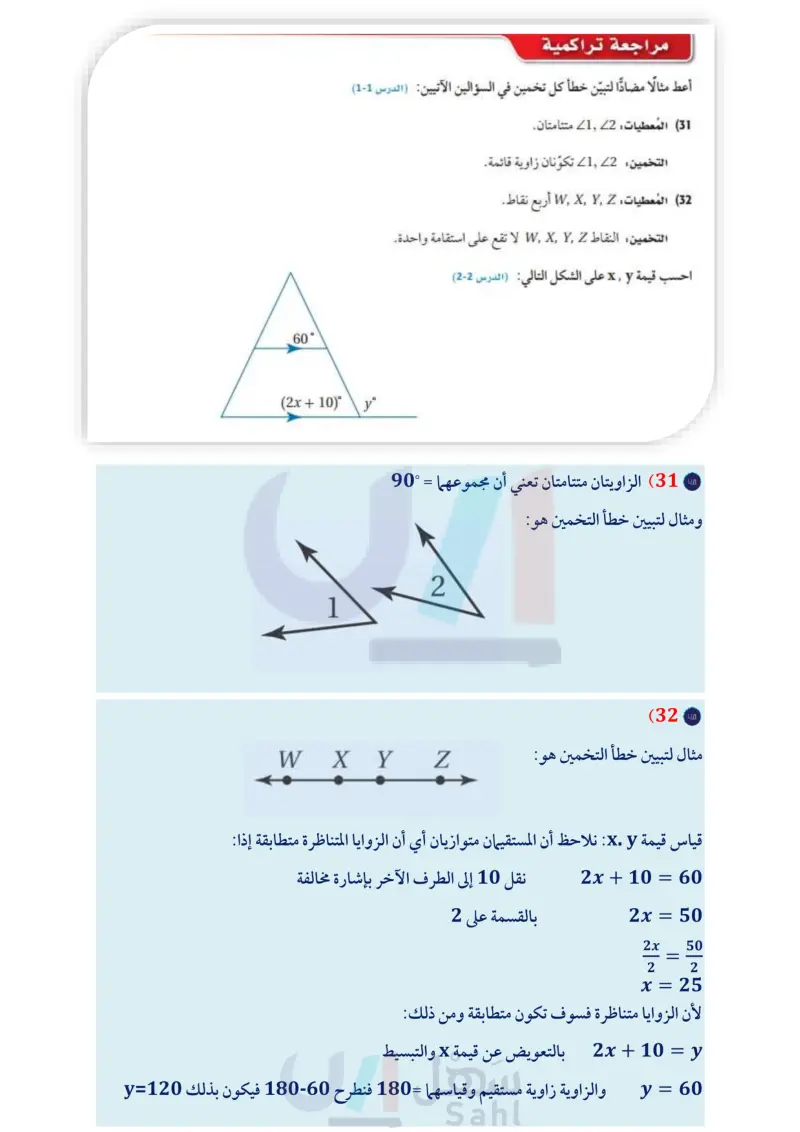
(27) تحد: استعمل الشكل المجاور. ( إذا كان : 180 = m 1 + m2، فبرهن أن a || c. إذا كان : a | | c و 180 = m21 + m23، فبرهن أن t i c . LO 5 6 (28) اكتب لخص الطرائق الخمس التي استعملت في هذا الدرس لإثبات توازي مستقيمين. 4 32 t 1 ما 2 3 4 6 7 8 10 0 11 12 m تدريب على اختبار (29) أي الحقائق الآتية كافية لإثبات أن المستقيم d يوازي XZ ؟ (30) استعمل الشكل المجاور Y d 3 2 21 = 23 A 23 = ZZ B 21 = ZZ C Z 22 = ZX D لتحديد أن صحة أي مما يأتي ليست مؤكدة: 24 = 27 A X B 4 و 8 متكاملتان l || m C و D 5 و 6 متکاملتان 16-12 15-11 (35 الدرس 3-2- إثبات توازي مستقيمين ال107م Ministry of Education 2024-1446 60° (2x + 10)° مراجعة تراكمية أعط مثالا مضادا لتبيّن خطأ كل تخمين في السؤالين الآتيين ( الدرس (1-1) 31 المعطيات : 12 متتامتان. التخمين: 12 تكوّنان زاوية قائمة. 32 المعطيات: أربع نقاط. , التخمين: النقاط ,,,,,, لا تقع على استقامة واحدة. احسب قيمة x y على الشكل التالي (الدرس (2-2) , y° -11 - 4 12-(-9) (34 استعد للدرس اللاحق بسط كلًا من العبارات الآتية : 6-5 4-2 (33

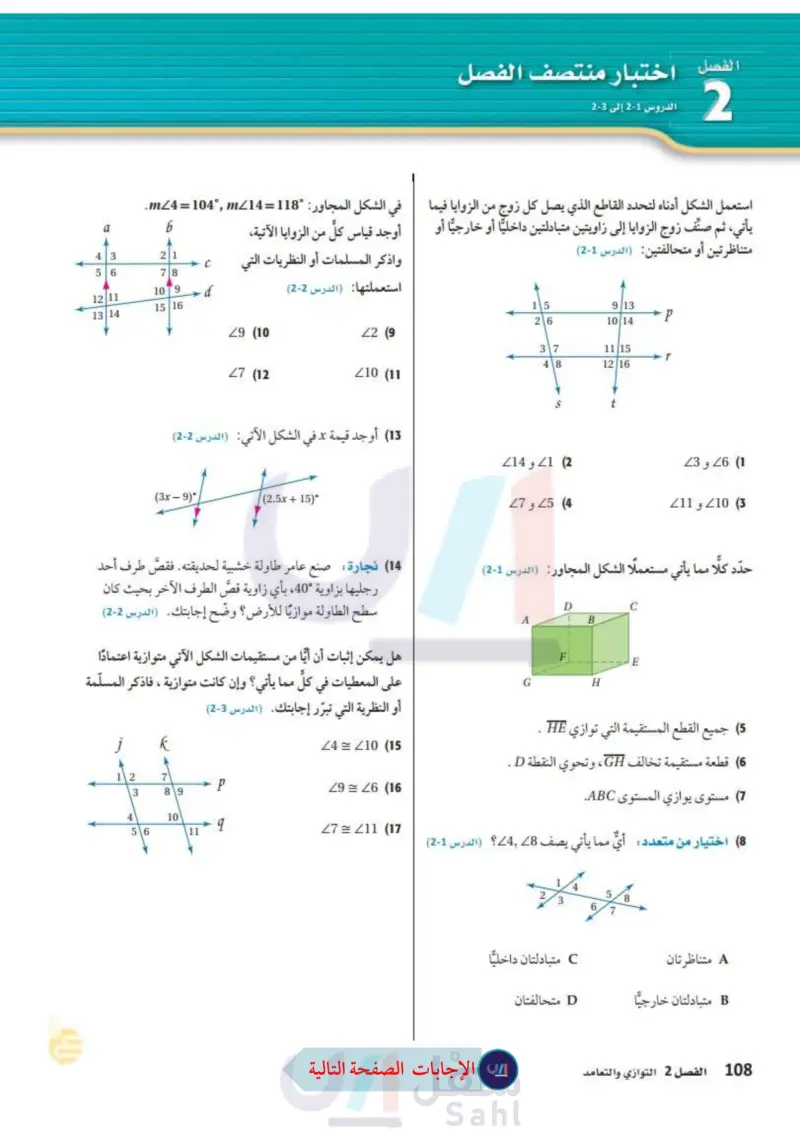
الفصل اختبار منتصف الفصل 2 الدروس 1-2 إلى 3-2 a 6 43 21 56 78 12 11 1079 15 16 d استعمل الشكل أدناه لتحدد القاطع الذي يصل كل زوج من الزوايا فيما في الشكل المجاور: °118=m24=104°, m214. يأتي، ثم صنف زوج الزوايا إلى زاويتين متبادلتين داخليًا أو خارجيًا أو أوجد قياس كل من الزوايا الآتية، متناظرتين أو متحالفتين: الدرس (1-2) واذكر المسلمات أو النظريات التي استعملتها (الدرس (2-2) 15 9 13 13 14 P 26 10 14 29 (10 Z2 (9 37 11 15 48 12 16 27 (12 210 (11 13 أوجد قيمة x في الشكل الآتي: (الدرس (2-2) (3x-9)° (2.5x+15)° t 1) 26 و 23 2) 21 و 214 3) 10 و 211 4) 25 و 27 حدد كلًا مما يأتي مستعملا الشكل أدناه: (الدرس 1-2) D C B A F E G H (14) نجارة صنع عامر طاولة خشبية لحديقته. فقص طرف أحد رجليها بزاوية 40 ، بأي زاوية قصَّ الطرف الآخر بحيث كان سطح الطاولة موازيًا للأرض؟ وضّح إجابتك (الدرس (2-2) هل يمكن إثبات أن أيا من مستقيمات الشكل الآتي متوازية اعتمادًا على المعطيات في كل مما يأتي؟ وإن كانت متوازية ، فاذكر المسلّمة أو النظرية التي تبرّر إجابتك (الدرس (3-2) وزارة التعليم Ministry of Education 2024-1446 j 24 = 210 (15 12 7 P 3 89 29 = 26 (16 4 10 q 56 11 27 = 211 (17 (5 جميع القطع المستقيمة التي توازي HE 6 قطعة مستقيمة تخالف GH ، وتحوي النقطة D . (7) مستوى يوازي المستوى ABC. اختيار من متعدد : أي مما يأتي يصف 4 الدرس (1-2) = 1 5 8 3 6 7 A متناظرتان C متبادلتان داخليا B متبادلتان خارجيًا D متحالفتان الفصل 2 التوازي والتعامد 108