المساحات في المستوى - التفاضل والتكامل - ثالث ثانوي
الوحدة الأولى: الاشتقاق وتطبيقاته
الوحدة الثانية: تفاضل وتكامل الدوال الأسية واللوغاريتمية
الوحدة الثالثة: سلوك الدالة ورسم المنحنيات
الوحدة الرابعة: التكامل المحدد وتطبيقاته
Mustafa Alselk
- ناصر سالم 01:45
04:46
(2)
4.5
فكر وناقش نظرية
أولا: مساحة منطقة محددة بمنحنى الدالة د ومحور السينات في الفترة
مثال1: المساحة تحت المنحنى
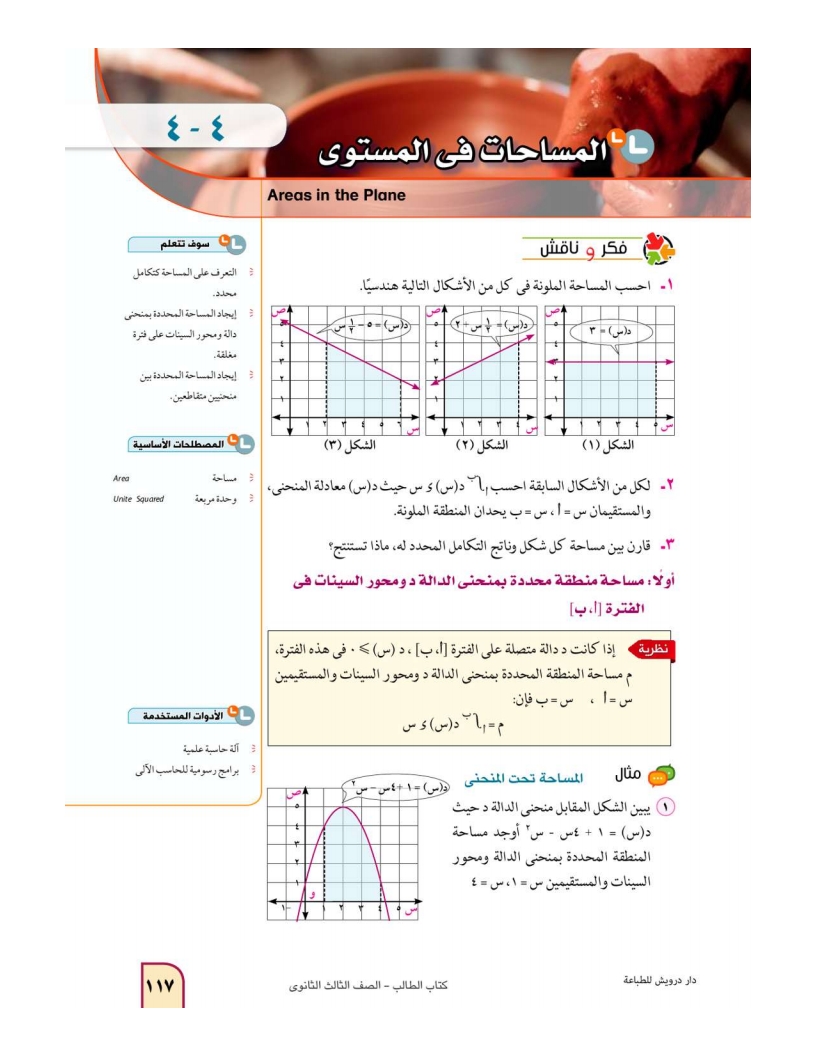
سوف تتعلم
المصطلحات الأساسية
الأدوات المستخدمة
تابع مثال1: المساحة تحت المنحنى
تفكير ناقد لاحظ أن
مثال2: المساحة فوق محور السينات ومنحنى الدالة
حاول أن تحل1: أوجد مساحة المنطقة المحددة بمنحنى الدالة د ومحور السينات والمستقيمين
حاول أن تحل2: أوجد مساحة المنطقة المحددة بمنحنى الدالة د(س)
مثال3: المساحة بين منحنى ومحور السينات
ملاحظة هامة: لتعيين المساحة بين منحنى الدالة ومحور السينات والمستقيمين
حاول أن تحل3: أوجد مساحة المنطقة المستوية المحددة بالمنحنى
مثال4: تطبيقات معمارية للمساحة
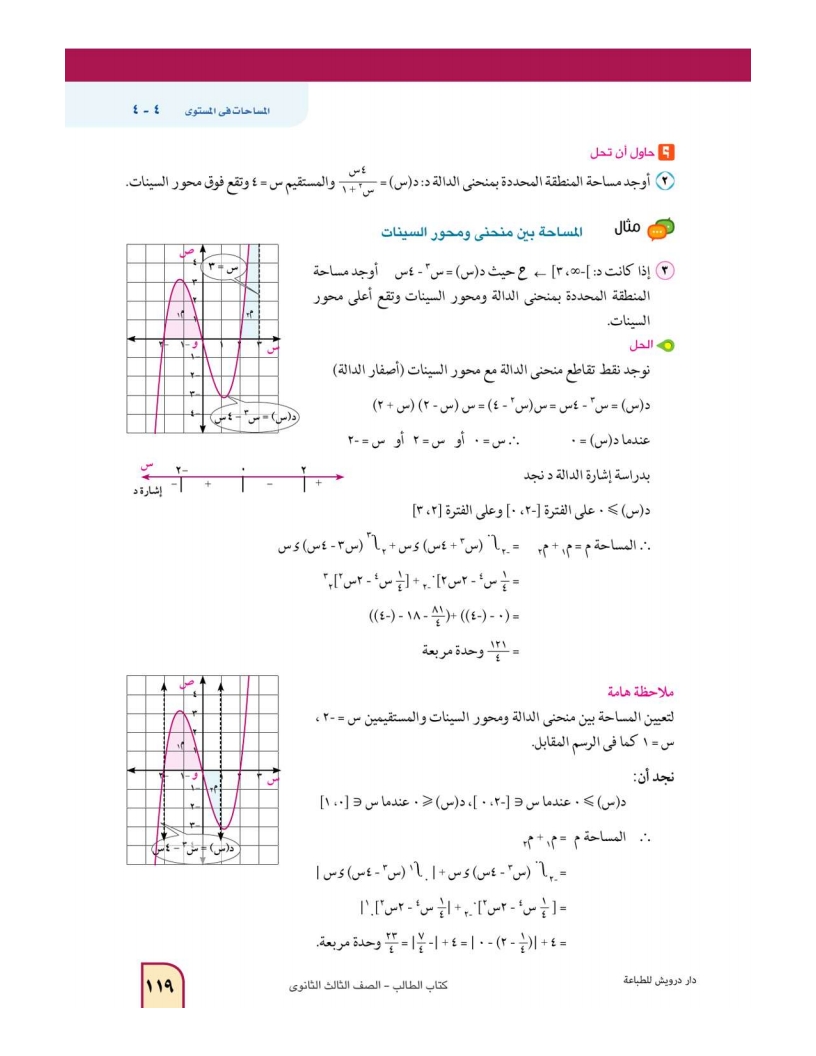
تفكير ناقد: أوجد مساحة المنطقة المستوية المحددة بالمنحنى
حاول أن تحل4: أوجد تكلفة تغطية الممرات الخمسة
ثانياً: مساحة المنطقة المستوية المحصورة بين منحنيين
مثال5: مساحة منطقة بين منحنيين متقاطعين
تابع مثال5: مساحة منطقة بين منحنيين متقاطعين
مثال6: تعدد المناطق بين منحنيين ومتقاطعين
حاول أن تحل5: أوجد مساحة المنطقة المحددة بمنحنى الدالتين د , ر حيث
حاول أن تحل6: احسب المساحة اللازمة من الورق اللاصق
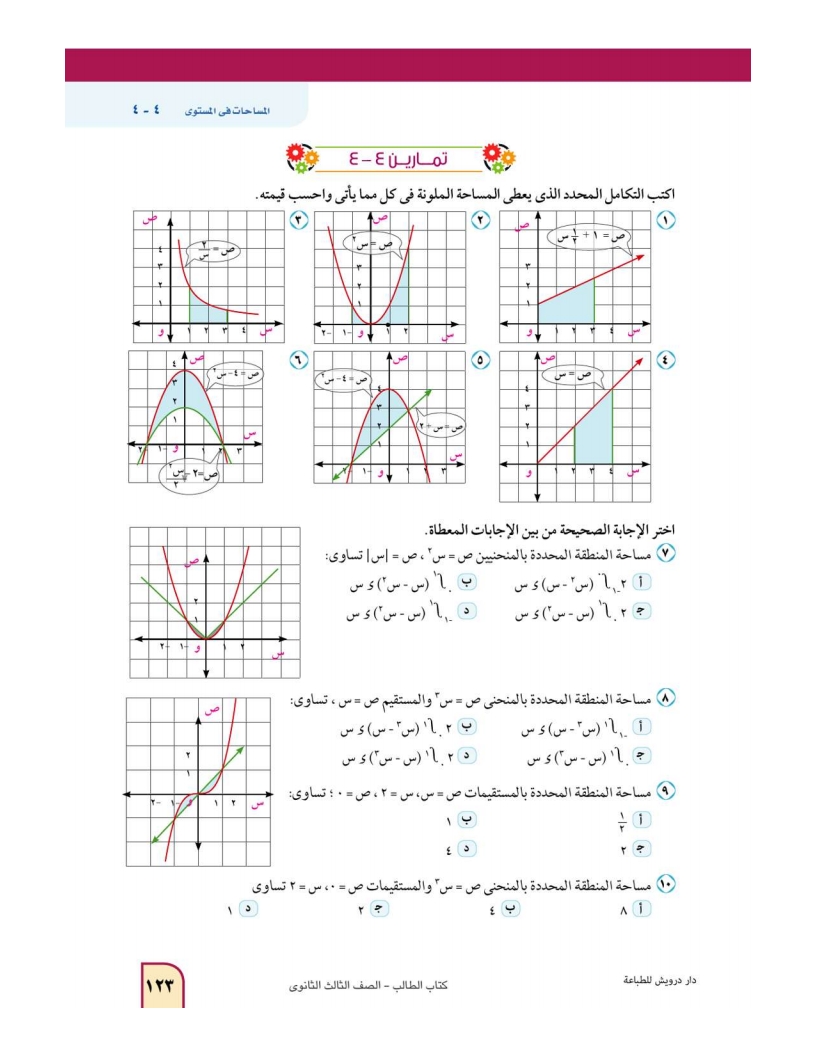
تمارين 4-4: اكالملونة في كل مما يأتي واحسب قيمتهتب التكامل المحدد الذي يعطي المساحة
اختر الإجابة الصحيحة من بين الإجابات المعطاة
في كل مما يأتي احسب مساحة المنطقة المستوية المحصورة بين
تفكير إبداعي: في الشكل المقابل أوجد مساحة المنطقة المحددة بمنحنى الدالة د والمستقيمين
لم يتم إضافة أي تعليقات حتى الآن.
الرجاء تسجيل الدخول لكتابة تعليق
