اللوغارتم الطبيعي - الرياضيات العلمي - سادس اعدادي
الفصل الأول: الأعداد المركبة
الفصل الثاني: القطوع المخروطية
الفصل الثالث: تطبيقات التفاضل
الفصل الرابع: التكامل
الفصل الخامس: المعادلات التفاضلية الاعتيادية
الفصل السادس: الهندسة الفضائية

اللوغارتم الطبيعي
تعريف اللوغارتم الطبيعي

المبرهنة الأساسية لحساب التكامل
إذا كان y=ln(3x^2+4) فأوجد dy/dx

جد ∫cosθdθ/1+sinθ
دالة اللوغارتم الطبيعي
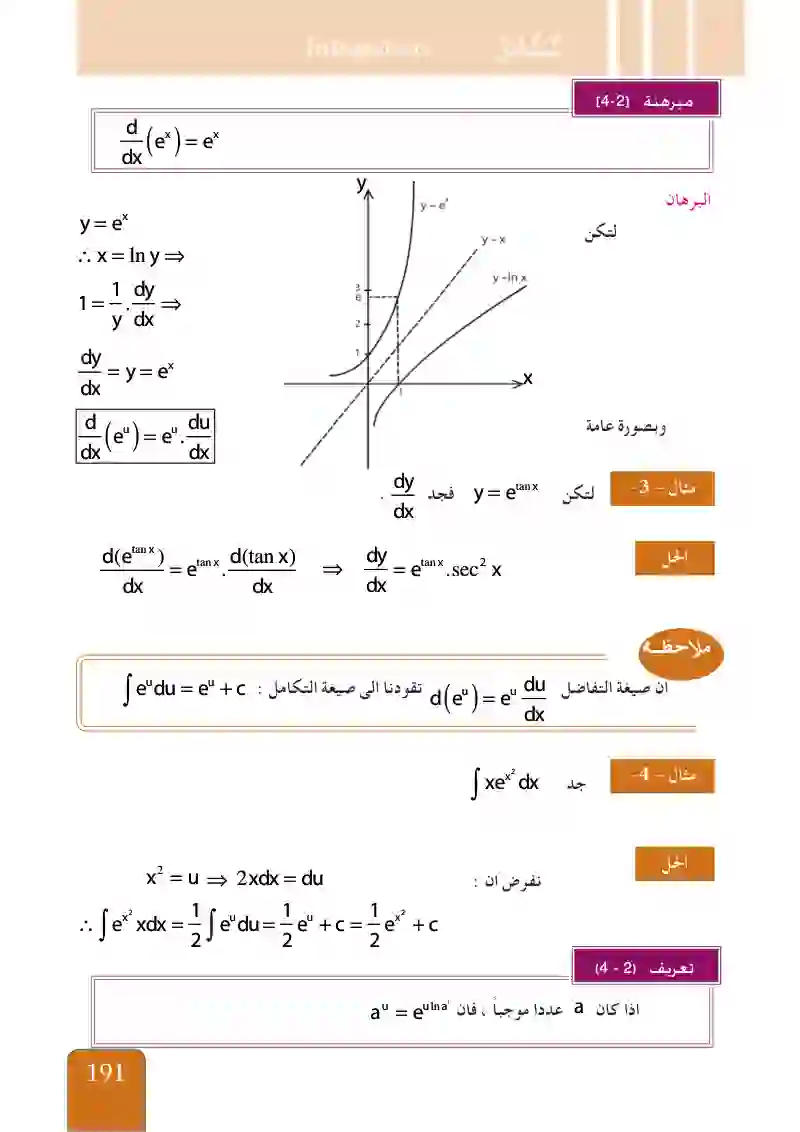
مبرهنة دالة دالة اللوغارتم الطبيعي d/dx(e^x)=e^x
لتكن y=e^tan x فجد dy/dx
صيغة التفاضل تقودنا لصيغة التكامل
جد ∫xe^x^2 dx
إذا كان a عددا موجبا فإن a^u=e^u ln a

مبرهنة da^u/dx=a^u.du/dx ln a
جد dy/dx لكل مما يأتي y=3^2x-5

جد dy/dx لكل مما يأتي y=ln3x
جد التكاملات الآتية ∫3 0 1/x+1 dx

أثبت أن ∫4 -2 |3x-6|dx=30
f(x) دالة مستمرة على الفترة [-2,6] فإذا كان ∫6 1 f(x)dx=6 وكان ∫6 -2 [f(x)+3]dx=32 فجد ∫1 -2 f(x)dx
جد قيمة a∈R إذا علمت أن ∫a 1 (x+1/2)dx=2∫∏/4 0sex^2 x dx
إذا كان للمنحني f(x)=(x-3)^3+1 نقطة انقلاب (a,b) جد القيمة العددية للمقدار ∫b 0 f`(x)dx-∫a 0 f``(x)dx
لتكن f(x)=x^2+2x+k حيث k∈R دالة نهايتها الصغرى تساوي (-5) جد ∫3 1 f(x)dx





