المقارنة بين أطوال الأضلاع في المثلث - رياضيات 1 - ثاني اعدادي
الوحدة الأولى: الأعداد الحقيقية
الوحدة الثانية: العلاقة بين متغيرين
الوحدة الثالثة: الإحصاء
الوحدة الرابعة: متوسطات المثلث والمثلث المتساوي الساقين
الوحدة الخامسة: التباين
كتاب النشاط
الأنشطة والتدريبات
الوحدة الأولى: الأعداد الحقيقية
الوحدة الثانية: العلاقة بين متغيرين
الوحدة الثالثة: الإحصاء
الوحدة الرابعة: متوسطات المثلث والمثلث المتساوي الساقين
المثلث أ ب ج فيه ق الزاوية أ = 40 ، ق الزاوية ب = 75 ، رتب اطوال أضلاع المثلث تنازلياً
في الشكل المقابل برهن أن ب ج> أج
في الشكل المقابل برهن أن ب ج> أب
في الشكل المقابل برهن أن أ ج > د ب
في الشكل المقابل برهن أن أ ب > ب ج
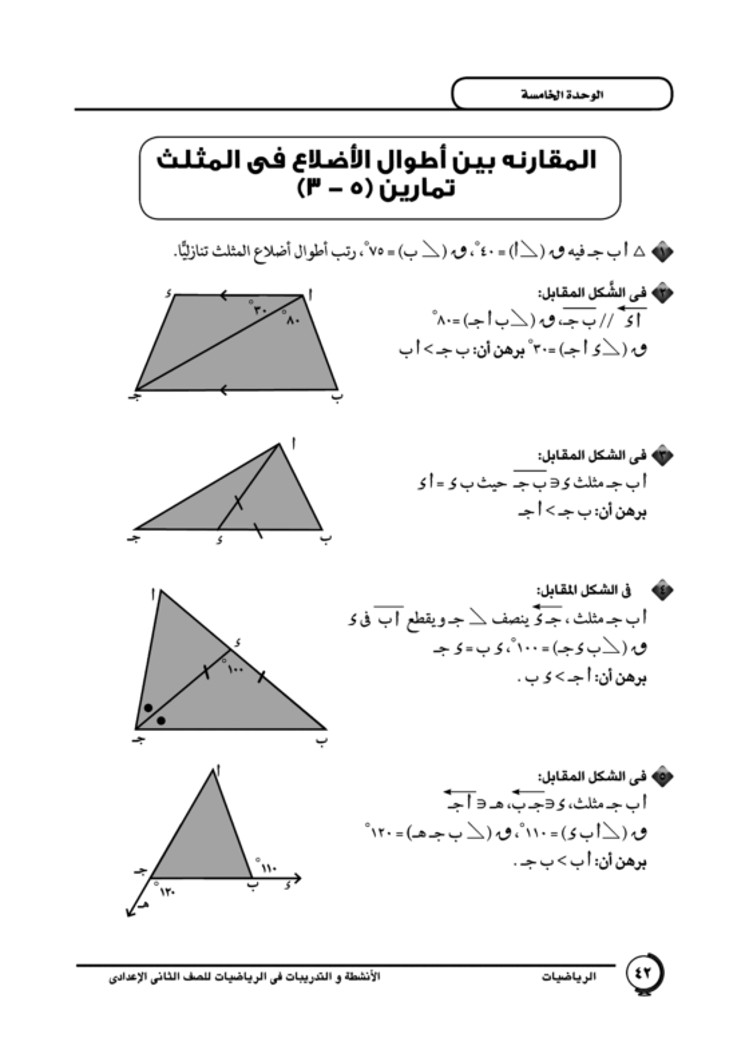
في الشكل المقابل برهن أن أ ب > ج د
في الشكل المقابل برهن أن أ ه> أ د
أ ب ج مثلث ج د ينصف الزاوية ج ، ج د تقاطع أ ب =(د) برهن أن ب ج > ب د
المثلث أ ب ج فيه ق الزاوية أ = (5 س+ 2) ، ق الزاوية ب =(6 س - 10) ، ق الزاوية ج =( س+ 20) رتب أطوال أضلاع المثلث تصاعديا
أ ب ج مثلث قائم الزاوية في ب ، د ينتمي إلى أ ج ، ه تنتمي إلى ب ج ، بحيث أ د = د ه ، أثبت أن ق الزاوية( ج ه د) > ق الزاوية( ج د ه)
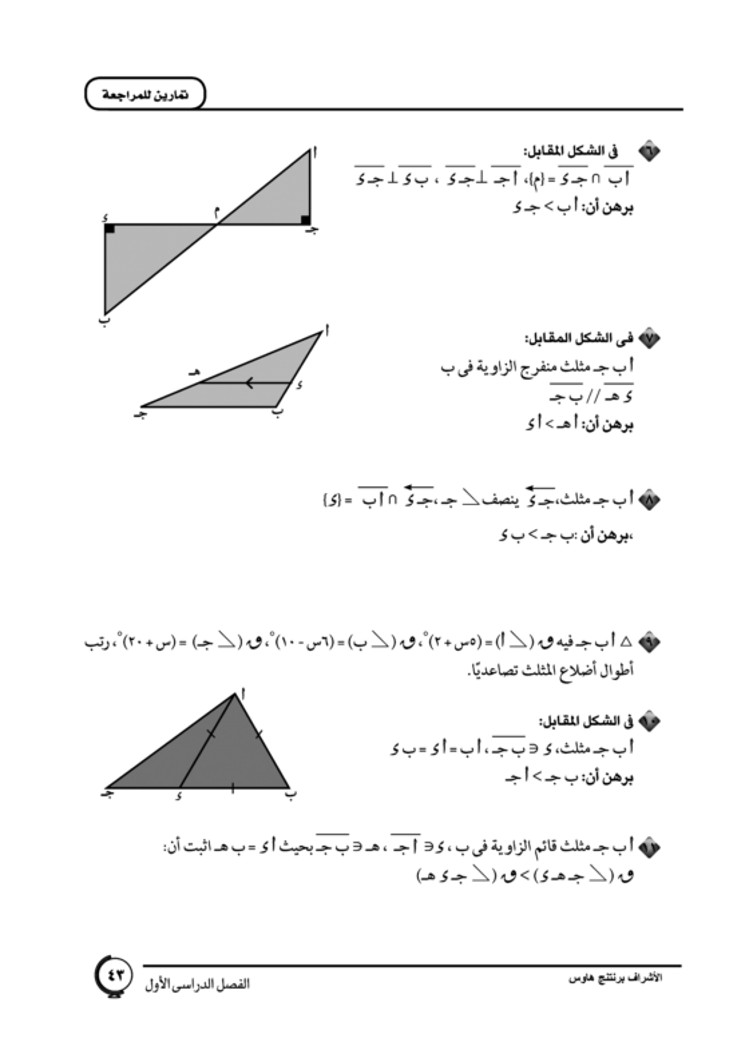
في الشكل المقابل برهن أن ب ج> أ ج






