قانون قاعدة جيب التمام - الرياضيات العامة 1 - ثاني ثانوي
الوحدة الأولى: الدوال الحقيقية ورسم المنحنيات
الوحدة الثانية: الأسس واللوغاريتمات وتطبيقات عليها
الوحدة الثالثة: النهايات
الوحدة الرابعة: حساب المثلثات

قانون (قاعدة) جيب التمام

نص قانون جيب التمام
ايجاد طول ضلع مجهول في مثلث
إيجاد قياس زاوية في المثلث إذا علمت أطوال أضلاعه الثلاثة

استخدام قاعدة جيب التمام لأي مثلث في إيجاد قياس زاوية مجهولة - مثال2
أوجد قياس أكبر زاوية في المثلث ل من إذا علم أن ل = 7. 5 سم م = 12سم ن= 17.5 سم ومن ذلك أثبت انه

استخدام قانون جيب التمام في حل المثلث - مثال4
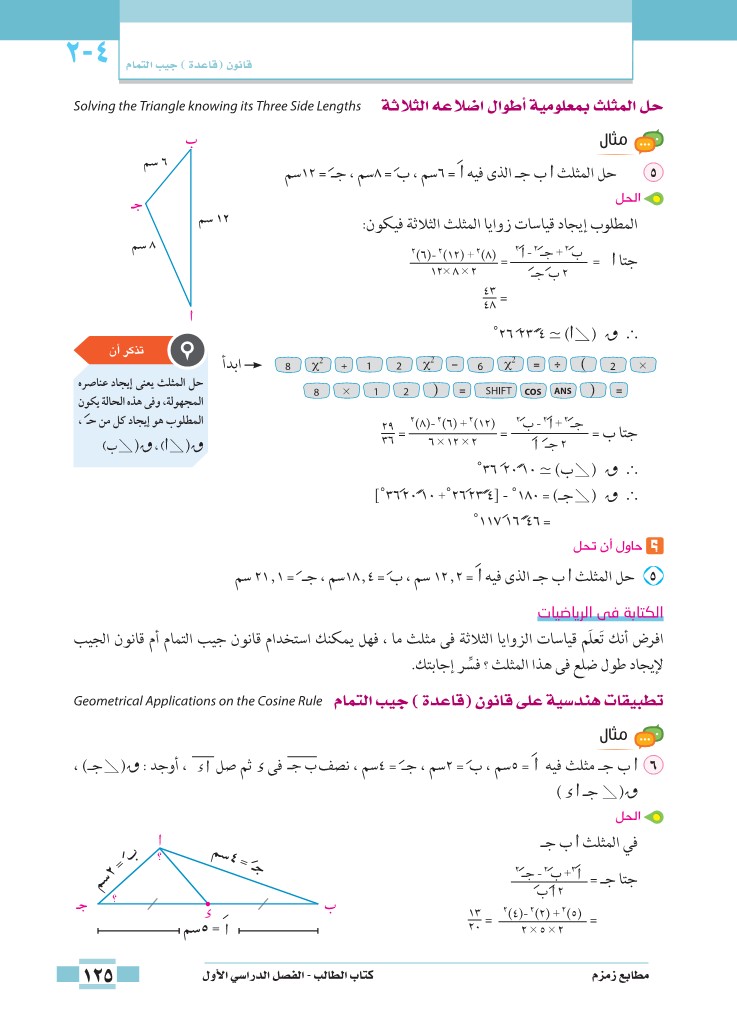
حل المثلث بمعلومية أطوال أضلاعه الثلاثة
تطبيقات هندسية على قانون جيب التمام - مثال6

تابع تطبيقات هندسية على قانون جيب التمام - مثال6
مثال7 الربط بالهندسة

لكل من المثلثات التالية اكتب الصيغة الصحيحة لقانون الجيب أو قانون جيب التمام الزاوية
تطبيقات حياتية على قانون جيب التمام - مثال8

في إحدى مباريات كرة القدم كان لاعب خط الوسط علي بعد 20 مترا من لاعب الجناح الأيمن
مثال10 قياس المسافة بطريقة غير مباشرة

في اي مثلث س ص ع يكون
مثلث اطوال أضلاعه 13, ,15 ,17 من السنتيمترات ,فإن قياس أ صغر زواياه هو
مثلث أطوال أضلاعه 5.7 سم , 7,5 سم , 4,2 سم فغن أصغر زواياه هو
في المثلث ل من يكون م+ ن - ل =
قياس أكبر زوايا في المثلث الذي أطوال أضلاعه 7,5,3
في اي مثلث ل م ن يكون المقدار
في المثلث س ص ع يكون ص + ع - س = 2 ص ع
في المثلث ا ب ج = 2:2:3 فإن جتا أ تساوي
استخدام قانون جيب تمام الزاوية لإيجاد قيمة س لأقرب جزء من عشرة

في المثلث ا ب ج يكون
أ ب ج د مثلث فيه ا ب = 16 سم أ ج= 24 سم ق الزاوية أ = 80 أوجد طول ب ج وإذا كان ا د ينصف الزاوية د من الداخل
قطعة ارض على شكل مثلث أطوال أضلاعه 300م , 210 م ,140 م استخدم قانون جيب التمام لإيجاد مساحة قطعة الأرض مقربا لأقرب متر مربع
ا ب ج د شكل رباعي فيه ب ج يساوي 78 سم ج د 96 سم قياس الزاوية ب ج د = 97 سم فياس الزاوية
أ ب ج د متوازي أضلاع فيه أ ب = 12 سم ب ج =12سم طول القطر بد = 14سم أوجد طول القطر أ ج لأقرب سنتيمتر
أب ج د شكل رباعي فيه اب = 15سم ب ج = 20 سم ج د =16 سم أ ج = 25 سم
أ ب ج د شكل رباعي فيه أ ب = 3 سم أ ج = 8 سم ب ج= 7 سم ج د 5 سم أثبت أن الشكل الرباعي دائري
ا ب ج مثلث فيه أ =9 سم ب = 15سم ,ج 21سم, أوجد قياس أكبر زاوية في هذا المثلث , أثبت أنها تحقق العلاقة
مثلث ا ب ج فيه أ =3 سم ب = 5 سم ج = جذر 19 سم أوجد

إذا كان النسبة بين جيوب زاويا مثلث هي 6:5:4 أوجد النسبة بين جيوب تمام زوايا هذا المثلث
في المثلث س ص ع إذا كان ص = ع- س أثبت أن قياس الزاوية ص = 60
في المثلث ا ب ج إذا كان ح-أ = 26 سم , ب =28 سم أ = 98 سم حيث 2ح هو محيط المثلث , فأوجد أطوال أضلاع المثلث
أ ب ج مثلث فيه ح -أ= 8 سم ح - ب = 4 سم فأوجد قياس أكبر زاوية في المثلث حيث 2 ح= أ+ب+ج
ضلعان من أضلاع مثلث طولاهما (جذر 10 + 2) , (جذر 10- 2) والزاوية المحصورة بينهما 60 أوجد طول الضلع الثالث
أب ج مثلث فيه أ = 5 سم ب = 10 سم ج = 7سم ق الزاوية أ = 27,66
قارن بين الحالات التي تستطيع فيه استخدام قانون الجيب لحل المثلث بتلك التي تستطيع فيها استخدام قانون جيب التمام
يركب كريم دراجته ليقطع المسافه من النقطة أ إلى ب ثم إلى النقطة ج بسرعة 28 كم /ساعة ثم يعود من النقطة ج إلى النقطة أ مباشره

مساحة المثلث
استخدام قانون جيب التمام في حل المثلث
للمثلث سته عناصر هي ثلاث أضلاع وثلاث زوايا
قانون قاعدة الجيب
قانون قاعدة جيب التمام

في المثلث ا ب ج إذا كان أ = 12 , ب = 28 , ج= 20 ق الزاوية ب تساوي
أوجد بدون استخدام الآلة الحاسبة قيمة كل مما يأتي
أوجد القيمة الدقيقة لكل مما يأتي
في المثلث س ص ع إذا كان س = 10 سم ق الزواية =30 ق الزاوية ص = 45 فأوجد ص
في المثلث ا ب ج يكون ب مساويا
في اي مثلث ل م ن يكون المقدار مساويا
نصف قطر الدائرة المارة برؤوس المثلث أ ب ج الذي فيه ق الزاوية أ = 60 ا = جذر 3 سم يكون طوله
العلاقة التي تربط بين ظاه تعطى على الصورة
إذا كان جا = 46 فإن قياس الزاوية بالدرجات يساوي
أي من الزوايا الآتية يكون الجيب وجيب التمام لها سالبان
بدون استخدام الآلة الحاسبة تكون قيمة جتا 120

في الشكل المقابل استخدم الطوال المعطاة في المثلث لتحقق من أن
حل المثلث المقابل مقربا طول الضلع إلى أقرب جزء من عشرة والزاوية إلى أقرب درجة
س ص ع مثلث فيه فيه قياس الزاوية س=2/3 ق الزواية ص 1/2 ق الزاوية ع وطول نصف قطر الدائرة المارة برؤوسه 10 سم أوجد محيط المثلث س ص ع
حل المثلث ا ب ج الذي فيه أ = 12 سم ,ق الزاوية ج = 66 ج= 5 سم مقربا الطول لأقرب سنتيمتر والزاوية لأقرب درجة
ا ب ج د شكل رباعي فيه أ ب = 8 سم , إ د = 10 سم قياس الزاوية أ = 82 ب ج =12 سم
الهرم الأكبر (هرم خوفو) هو أكثر آثار العالم إثارة للجدل والخيال حيث يعد نقله حضارية






