الدوائر الرقمية - الهندسة - ثاني ثانوي
1. أساسيات الهندسة
2. الهندسة الكهربائية
3. الدوائر الرقمية
4. محاكاة الدوائر الإلكترونية باستخدام دوائر تنكركاد
5. محاكاة نظام التحكم الدقيق
66 99 3. الدوائر الرقمية سيتعرف الطالب في هذه الوحدة على أسس الجبر المنطقـ البوليني، وسيتعرف أيضًا على كيفية استخدام مخططات كارنوف Karnaugh) ، وختامًا سيستخدم الطالب برنامج المحاكاة لرسم الدوائر المختلفة . أهداف التعلم بنهاية هذه الوحدة سيكون الطالب قادرًا على أن : > يتعرّف على أساسيات الدوائر الرقمية. > يتعرّف على قواعد الجبر البوليني. يُطبق الجبر البوليني لتبسيط الدوال. > يُميز بين البوابات المنطقية. ينشئ دوال منطقية من خلال دمج مجموعة من البوابات المنطقية معًا. يُطبق مخططات كارنوف لتبسيط التصاميم المنطقية. > يتعرف على المكونات الأساسية للدوائر الرقمية. يُحدد ماهية الدوائر المتكاملة Integrated Circuits-IC). > يُحاكي الدوائر الرقمية المصممة باستخدام برنامج ملتي سيم لايف Multisim Live). الأدوات > برنامج ملتي سيم لايف (Multisim (Live) وزارة التعليم Ministry of Education 2024-1446

الدوائر الرقمية
أهداف التعلم: الدوائر الرقمية
الأدوات: الدوائر الرقمية
الدرس الأول الدوائر الرقمية أساسيات الدوائر الرقمية Basics of the Digital Circuit رابط الدرس الرقمي www.ien.edu.sa تُستخدم الدوائر الرقمية لتنفيذ العمليات والمنطق البوليني في الأنظمة. الجدول 3.1 حالات الدوائر الرقمية يكمن الاختلاف الأساسي بين الدوائر الرقمية والدوائر الكهربائية في أن الإشارات الكهربائية تعمل بإشارات مستمرة حيث يتدفق التيار الكهربائي عبر الدائرة، بينما تكون مُدْخَلات الإشارات الرقمية في تلك الدوائر إحدى القيمتين 0 و1 . تُستخدم الدوائر الرقمية في الدوائر المتكاملة وفي وحدات التحكم الدقيقة لتخزين المعلومات وتنفيذ الدوال المنطقية بالتزامن مع ربطها بالدوائر الكهربائية. يوجد نوعان رئيسان للدوائر الرقمية الدوائر التوافقية Combinational circuits تستقبل هذه الدوائر مُدْخَلات وقيم، وتنتج مُخْرَجاتها بناءً على الدالة المنطقية التي صُممت. من أنواع الدوائر التوافقية الدامج (Multiplexer) : يستقبل مُدْخَلات متعددة من مصدر رقمي ويُخرج قيـمـة واحدة. المفرق (Demultiplexer): يستقبل قيمة مُدْخَلة واحدة ويُخرج قيمًا متعددة. المشفرات (Encoders) : تحول الإشارة المدخلة إلى نتيجة ثنائية مشفرة. > دوائر فك التشفير (Decoders) تعمل بشكل معاكس للمشفرات، فهي تعيد تكوين الإشارة الأصلية التي ينتجها المشفر. الدوائر المتسلسلة Sequential Circuits الحالة صواب خطأ الأرقام الثنائية 1 0 الجدول 3.2 المستويات الفولتية الشائعة المستوى المنطقي | الرقم الثنائي الجهد بالفولت 5 فولت 3.3 فولت 5 1 0 0 3.3 1 0 0 تستقبل هذه الدوائر المدخلات والمُخْرَجات التي أنتجت بواسطة المُخْرَجات السابقة للدائرة، ومن أمثلة الدوائر المتسلسلة ما يلي: القلابات (Flip-Flops): تُستخدم لتخزين الإشارات الرقمية المتسلسلة. العدادات (Counters تستخدم لعمليات العد والتنسيق والمتابعة للمكونات الأخرى بالدوائر. : معلومة يمكن العثور على الإشارات التماثلية Analog Signals) في كل مكان في الطبيعة، أما الإشارات الرقمية فهي إشارات من صنع الإنسان يكمن الاختلاف بين هذين النوعين من الإشارات في أن الإشارات التماثلية تتباين في التردد والسعة الموجية، بينما تقتصر الإشارات الرقمية على حالتي التشغيل أو الإيقاف، واللتان يتم تمثيلهما بالقيم 0 و 1 . يُطلق على هذا التمثيل اسم النظام الثنائي. 67 وزارة التعليم Ministry of Education 2024-1446

أساسيات الدوائر الرقمية
الدوائر التوافقية
الدوائر المتسلسلة
الإشارات التماثلية
68 الجبر البوليني Boolean Algebra يُعرف الجبر البوليني بتكونه من مجموعة تتألف من عنصرين: 0، 1، وبه تُستخدم العمليات المنطقية: عملية AND ويتم تمثيلها بالرمز (۰) ، وعملية OR ويتم تمثيلها بالرمز (()) ، وتتحقق هاتان العمليتان من القواعد الآتية: إذا كان العنصران A و B ينتميان إلى مجموعة {10} فإن: A+B = B + A = Y A.B=B.A = Y ينتمي المُخْرَج ۷ الخاص بعمليات ( + ) و ( ) إلى المجموعة {10}. خصائص عملية AND في الجبر البوليني خصائص عملية OR في الجبر البوليني قانون التوزيع في الجبر البوليني مثال: A . (B + C = AB+A.C A+ 1 = 1 . A+ (B C) = (A + B) (A + C) A + 0 = A A+ A = A A + A = 1 A.1 = A A.0=0 A A = A . ― AA = 0 إذا كانت 0 = A فإن 1 = A ، بينما إذا كانت 1 = A فإن 0 = A قانون النفي المزدوج A = A تنطبق القواعد المذكورة بنفس الشكل على منطق العمليات العملية التعبير وه A.B AND A+B OR قد تحتوي البوابات المنطقية على أكثر من مدخلين، ولكن لها مخرج واحد فقط. نظرية ديمورجان DeMorgan's Theory لتتمكن من حل بعض العمليات المعقدة، يمكنك استبدال كل عنصر بمتممه وتغيير كل عملية AND إلى OR أو العكس. النظرية (ABC) = A + B + C (A + B + C = AB.C وزارة التعليم Ministry of Education 2024-1446

الجبر البوليني
نظرية ديمورجان
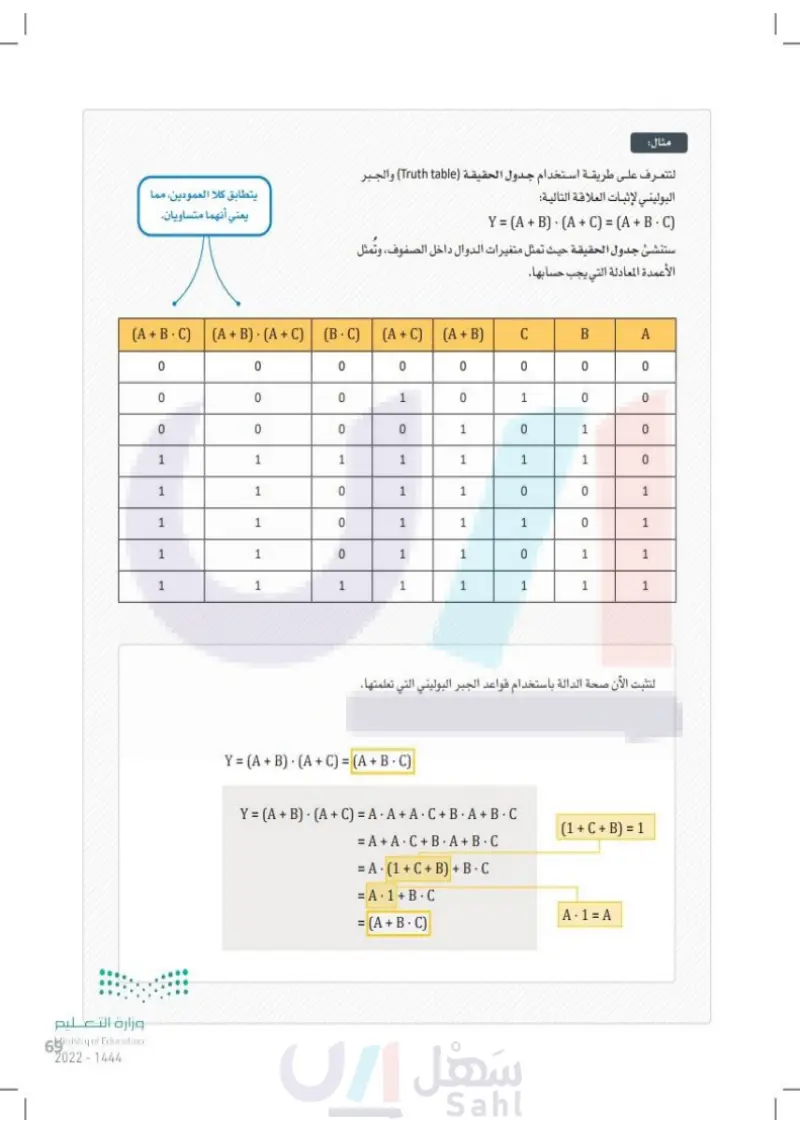
69 وزارة التعليم Ministry of Education 2024-1446 مثال: لتتعرف على طريقة استخدام جدول الحقيقة (Truth Table) والجبر البوليني لإثبات العلاقة الآتية: Y = (A+B) (A + C) = (A + B · C) ستنشئ جدول الحقيقة حيث تمثل متغيرات الدوال داخل الصفوف، وتُمثل الأعمدة المعادلة التي يجب حسابها. قيم الإدخال يتطابق كلا العمودين، مما يعني أنهما متساويان. (A + B. C) (A + B) (A + C) | (BC) · (A + C) (A + B) C B A 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 1 0 1 0 1 1 1 1 1 1 1 0 1 1 0 1 1 0 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 لتثبت الآن صحة الدالة باستخدام قواعد الجبر البوليني التي تعلمتها. • Y = (A + B) (A + C) = (A + B C) . Y = (A + B) (A + C) = A· A+ A·C + B · A + B C = A + A C + B· A + B C . = A (1 + C + B) + B · C = A 1+ B C . = (A + B C) (1 + C + B) = 1 A 1=A

طريقة استخدام جدول الحقيقة
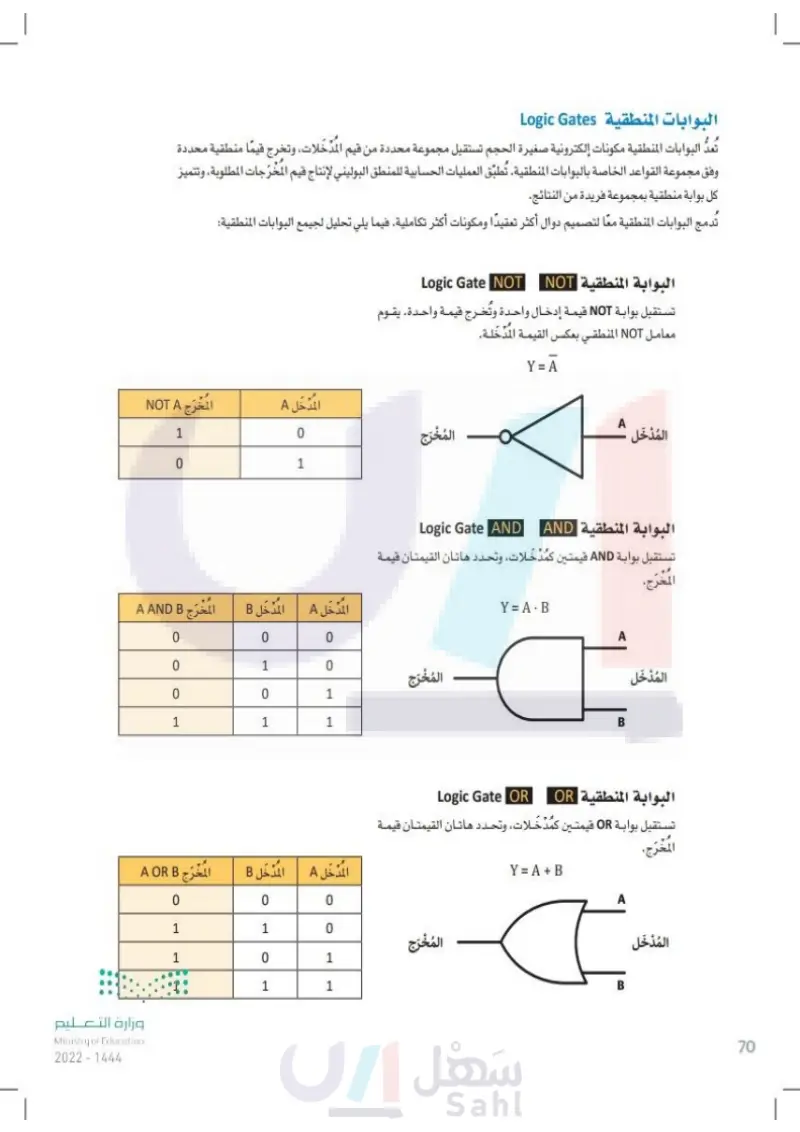
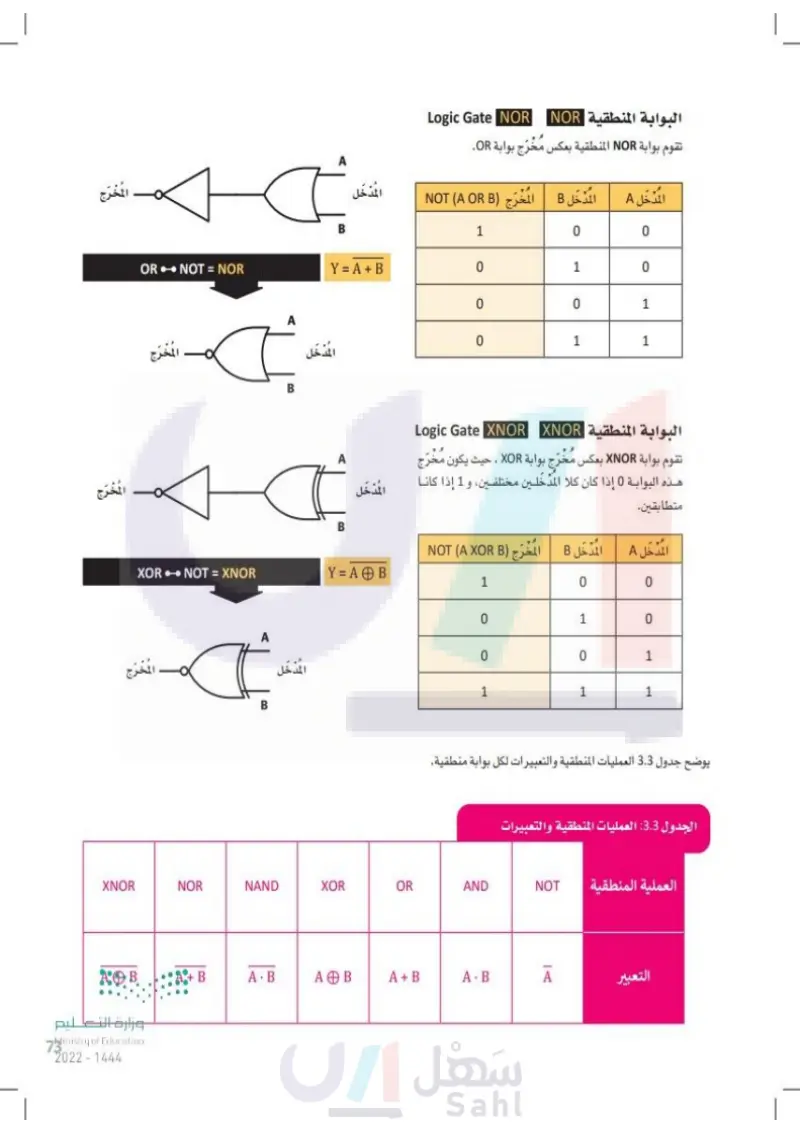
70 البوابات المنطقية Logic Gates تُعدُّ البوابات المنطقية مكونات إلكترونية صغيرة الحجم تستقبل مجموعة محددة من قيم المدخلات، وتخرج قيمًا منطقية محددة وفق مجموعة القواعد الخاصة بالبوابات المنطقية . تُطبّق العمليات الحسابية للمنطق البوليني لإنتاج قيم المخرجات المطلوبة، وتتميز كل بوابة منطقية بمجموعة فريدة من النتائج. تدمج البوابات المنطقية معًا لتصميم دوال أكثر تعقيدًا ومكونات أكثر تكاملية. فيما يلي تحليل لجيمع البوابات المنطقية: البوابة المنطقية NOT Logic Gate NOT تستقبل بوابة NOT قيمة إدخال واحدة وتُخرج قيمة واحدة. يقوم معامل NOT المنطقي بعكس القيمة المدخلة. المدخل A Y = A البوابة المنطقية AND A المخرج Logic Gate AND تستقبل بوابة AND قيمتين كمدخلات، وتحدد هاتان القيمتان قيمة المخرج. المُدْخَل Y = A.B A A.B B البوابة المنطقية OR Logic Gate OR المخرج تستقبل بوابة OR قيمتين كمُدْخَلات، وتحدد هاتان القيمتان قيمة المخرج. المُدْخَل Y = A + B ہیں B A + B المُخْرَج المدخل A المخرج NOT A 1 0 0 1 المدخل A المدخل B المخرج A AND B 0 0 0 0 1 0 0 0 1 1 1 1 المدخل المدخل B A المخرج A OR B 0 0 0 1 1 0 1 0 1 1 1 1 وزارة التعليم Ministry of Education 2024-1446

البوابة المنطقية NOT
البوابة المنطقية AND
البوابة المنطقية OR
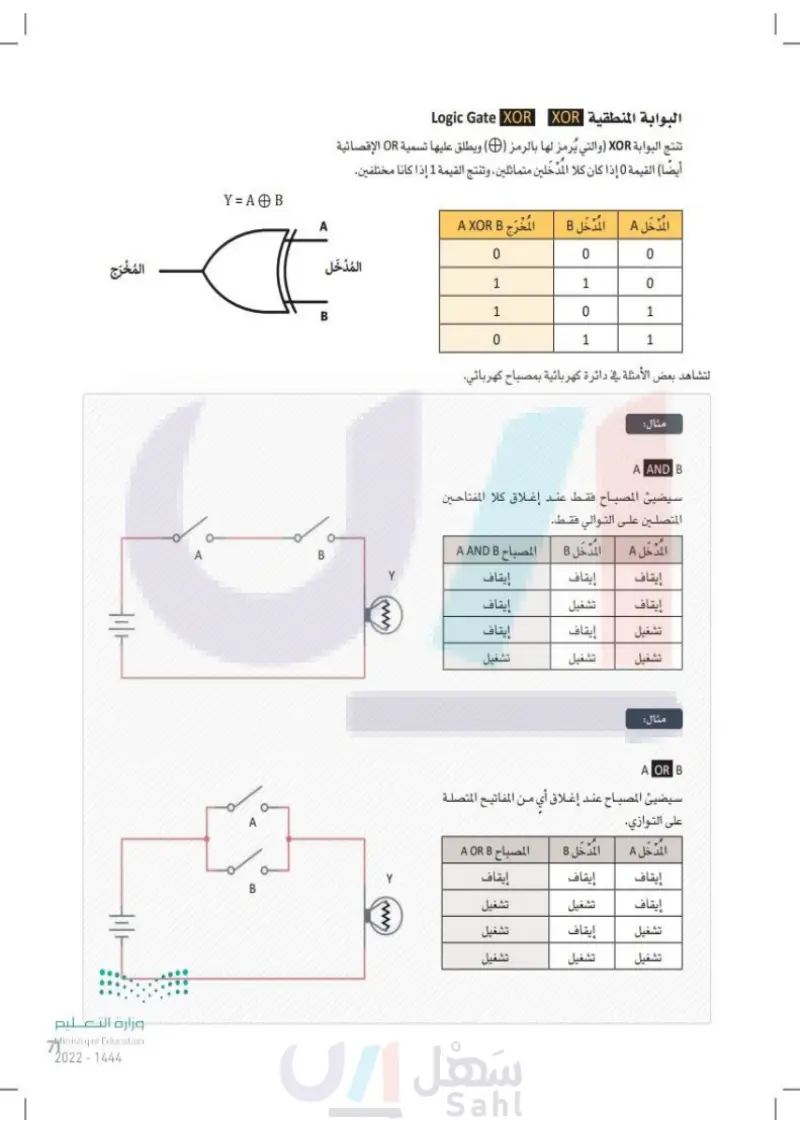
71 وزارة التعليم Ministry of Education 2024-1446 Hill tili الخرج AB A A البوابة المنطقية Logic Gate KOR XOR تنتج البوابة OR والتي يُرمز لها بالرمز (D) ويطلق عليها تسمية OR الإقصائية أيضًا) (القيمة 0 إذا كان كلا المدخلين متماثلين ، وتنتج القيمة 1 إذا كانا مختلفين. المدخل A المدخل B المخرج A XOR B Y=AB A I الْمُدْخَل B B Y WWW Y B ww 0 0 0 1 1 0 1 0 1 0 1 1 لتشاهد بعض الأمثلة في دائرة كهربائية بمصباح كهربائي. مثال: A AND B سيضيء المصباح عند إغلاق كلا المفتاحين المتصلين على التوالي فقط. المدخل A المدخل B المصباح A AND B إيقاف إيقاف إيقاف إيقاف تشغيل إيقاف تشغيل إيقاف إيقاف تشغيل تشغيل تشغيل مثال: A OR B سيضيء المصباح عند إغلاق أي من المفتاحين المتصلين على التوازي المدخل A المدخل B المصباح A OR B إيقاف إيقاف إيقاف إيقاف تشغيل تشغيل تشغيل إيقاف تشغيل تشغيل تشغيل تشغيل

البوابة المنطقية XOR
أمثلة في دائرة كهربائية بمصباح كهربائي
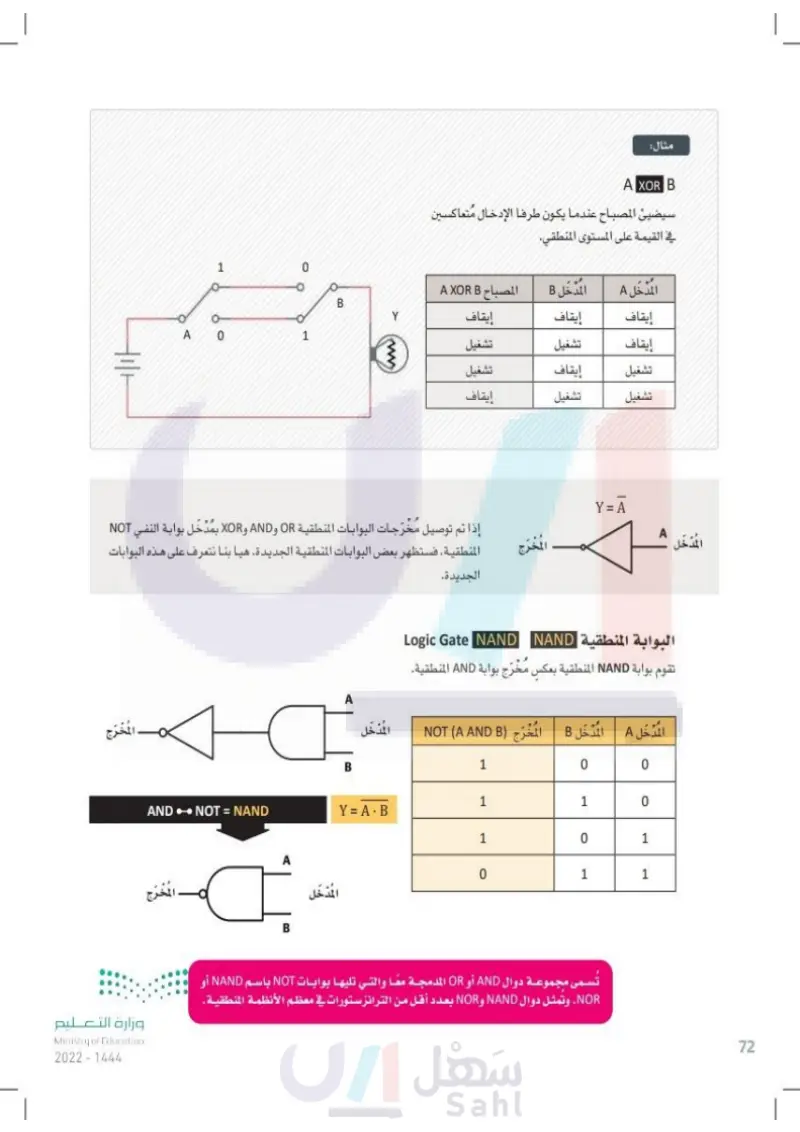
1 0 A 0 1 B Y مثال: A XOR B سيضيئ المصباح عندما يكون طرفا الإدخال متعاكسين في القيمة على المستوى المنطقي. المدخل A المدخل B المصباح A XOR B إذا تم توصيل مُخْرَجات البوابات المنطقية OR و AND و XOR بمدخل بوابة النفي NOT المنطقية ، فستظهر بعض البوابات المنطقية الجديدة هيا بنا نتعرف على هذه البوابات الجديدة. المخرج وزارة التعليم Ministry of Education 2024-1446 A A.B A.B AND •• NOT = NAND المخرج A.B A B B إيقاف إيقاف إيقاف إيقاف تشغيل تشغيل تشغيل إيقاف تشغيل تشغيل تشغيل إيقاف المُخْرَج Y = A A A المدخل البوابة المنطقية Logic Gate NAND NAND تقوم بوابة NAND المنطقية بعكس مُخْرَج بوابة AND المنطقية. المدخل المدخل B المخرج NOT (A AND B المُدْخَل A 1 0 0 1 1 0 Y=A.B 1 0 1 0 1 1 المُدْخَل تُسمى مجموعة دوال AND أو OR المدمجة معًا والتي تليها بوابات NOT باسم NAND أو NOR. وتمثل دوال NAND و NOR بعدد أقل من الترانزستورات في معظم الأنظمة المنطقية. 72

سيضيئ المصباح
مخرجات البوابات المنطقية
البوابة المنطقية NAND
73 المخرج المخرج A A + B A + B OR •• NOT = NOR المخرج A+B A B B Logic Gate NOR البوابة المنطقية NOR تقوم بوابة NOR المنطقية بعكس مُخْرَج بوابة OR. المدخل B المخرج (NOT (A OR B المدخل A المُدْخَل Y = A + B الدخل A AB AB B المُدْخَل XOR •• NOT = XNOR Y = A B المخرج AB A المُدْخَل شام B 1 0 0 0 1 0 0 0 ہے 1 0 1 1 البوابة المنطقية Logic Gate XNOR XNOR تقوم بوابة XNOR بعكس مُخْرَج بوابة XOR ، حيث يكون مُخْرَج هذه البوابة 0 إذا كان كلا المدخلين مختلفين، و 1 إذا كانا متطابقين. المدخل B المخرج NOT (A XOR B المدخل A 1 0 0 0 1 0 0 0 1 1 1 1 يوضح الجدول 3.3 العمليات المنطقية والتعبيرات لكل بوابة منطقية. الجدول 3.3 العمليات المنطقية والتعبيرات XNOR NOR NAND XOR OR AND NOT AB A + B A.B AB A + B A.B وزارة التعليم Ministry of Education 2024-1446 A العملية المنطقية التعبير

البوابة المنطقية NOR
البوابة المنطقية XNOR
جدول يوضح العمليات المنطقية والتغييرات لكل بوابة منطقبة
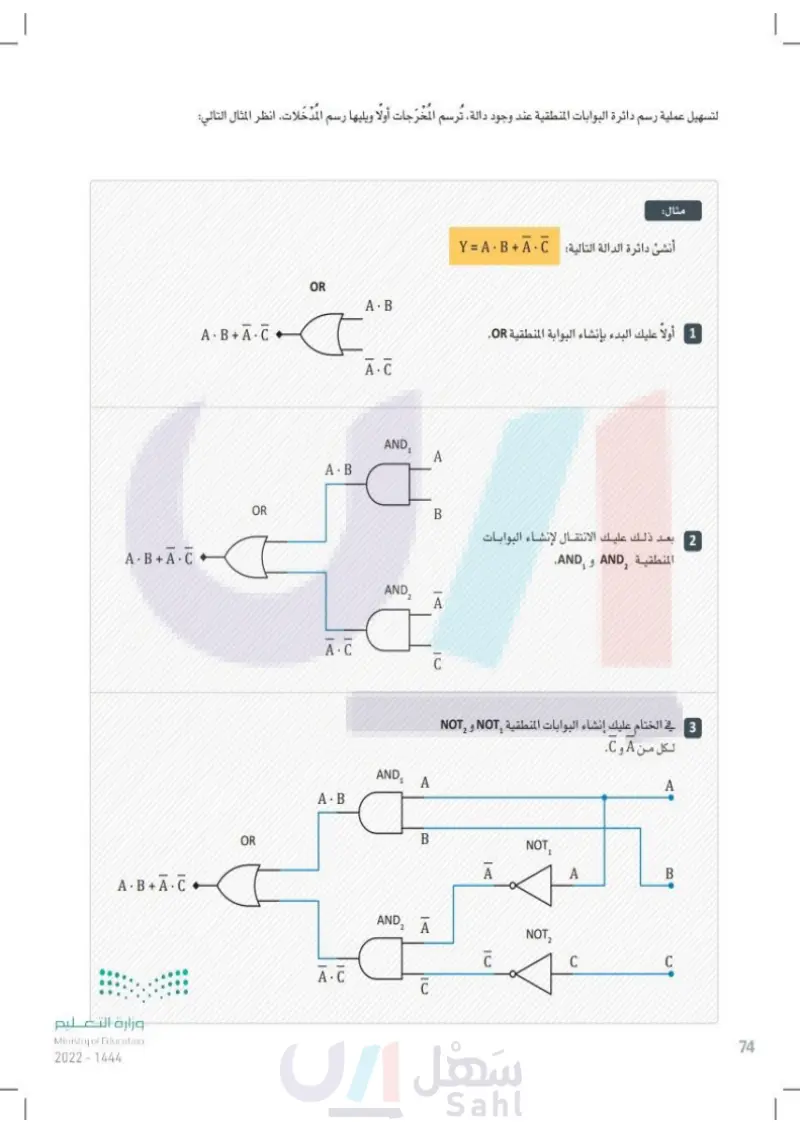
لتسهيل عملية رسم دائرة البوابات المنطقية عند وجود دالة، تُرسم المُخْرَجات أولًا ويليها رسم المدخلات. انظر المثال الآتي: AB+A.C OR C A.B A C A.B AND 1 A OR قتة B AB+A.C٠ وزارة التعليم Ministry of Education 2024-1446 A.B+A.C OR AND2 │A A.C C A.B A.C Y=A.B+A.C مثال: أنشئ دائرة الدالة الآتية: 1 أولا عليك البدء بإنشاء البوابة المنطقية OR بعد ذلك عليك الانتقال لإنشاء البوابات المنطقية AND و AND 1 في الختام عليك إنشاء البوابات المنطقية NOT و NOT لكل من A و C . 1 2 AND 1 A B AND, 2 A A NOT, 1 A A B C C NOT₂ 2 C C 2 74

تسهيل عملية رسم دائرة البوابات المنطقية عند وجود دالة
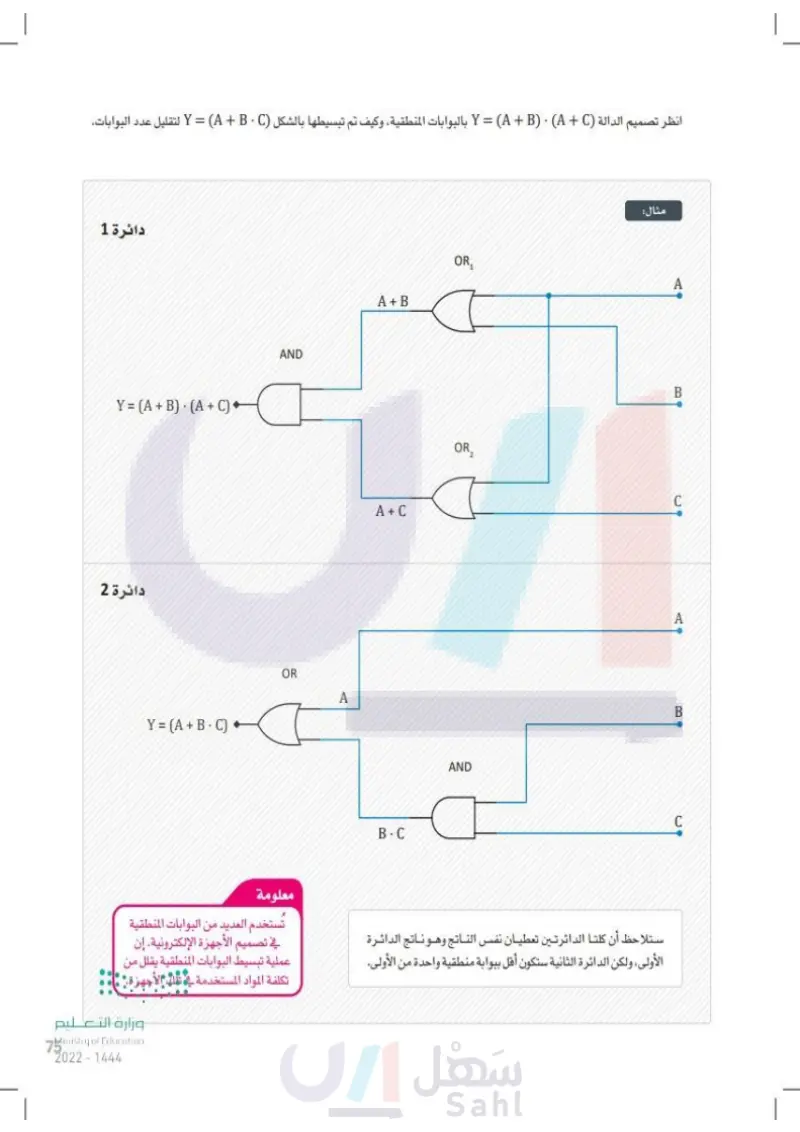
انظر تصميم الدالة Y = A + BAC بالبوابات المنطقية، وكيف تم تبسيطها باستخدام خاصية التوزيع لتصبح بالشكل B) (A + C) 75 دائرة 1 Y = (A + B) . (A + C) ' دائرة 2 وزارة التعليم Ministry of Education 2024-1446 Y = (A + B C . AND OR A A + B A+ C B.C OR₁₂ OR, AND Y ؛ لتقليل عدد البوابات. = (A + B C ) مثال: A B C A ستلاحظ أن كلتا الدائرتين تعطيان نفس الناتج وهو ناتج الدائرة الأولى، ولكن الدائرة الثانية ستكون أقل ببوابة منطقية واحدة من الأولى معلومة تُستخدم العديد من البوابات المنطقية في تصميم الأجهزة الإلكترونية. إن عملية تبسيط البوابات المنطقية يقلل من تكلفة المواد المستخدمة في تلك الأجهزة. B وں C

تصميم الدالة
وزارة التعليم Ministry of Education 2024-1446 تمرينات ما الفرق الرئيس بين الدائرة الرقمية والدائرة الكهربائية؟ 1 2 ما البوابة المنطقية التي تنتج دائمًا القيمة 1 عند وجود مُدْخَلات مختلفة (مثل: 0 = A و 1 = B)؟ صل نوع العملية في العمود الأول بالتعبير المنطقي المناسب في العمود الثاني. العملية التعبير المنطقي A.B NOT A+B AND A.B OR AB XOR A + B NAND AB NOR A XNOR 3 76

ما هو الفرق الرئيسي بين الدائرة الرقمية والدائرة الكهربائية؟
ما هي البوابة المنطقية التي تنتج دائما القيمة 1 عند وجود مدخلات مختلفة؟
صل نوع العملية في العمود الأول بالتعبير المنطقي المناسب في العمود الثاني
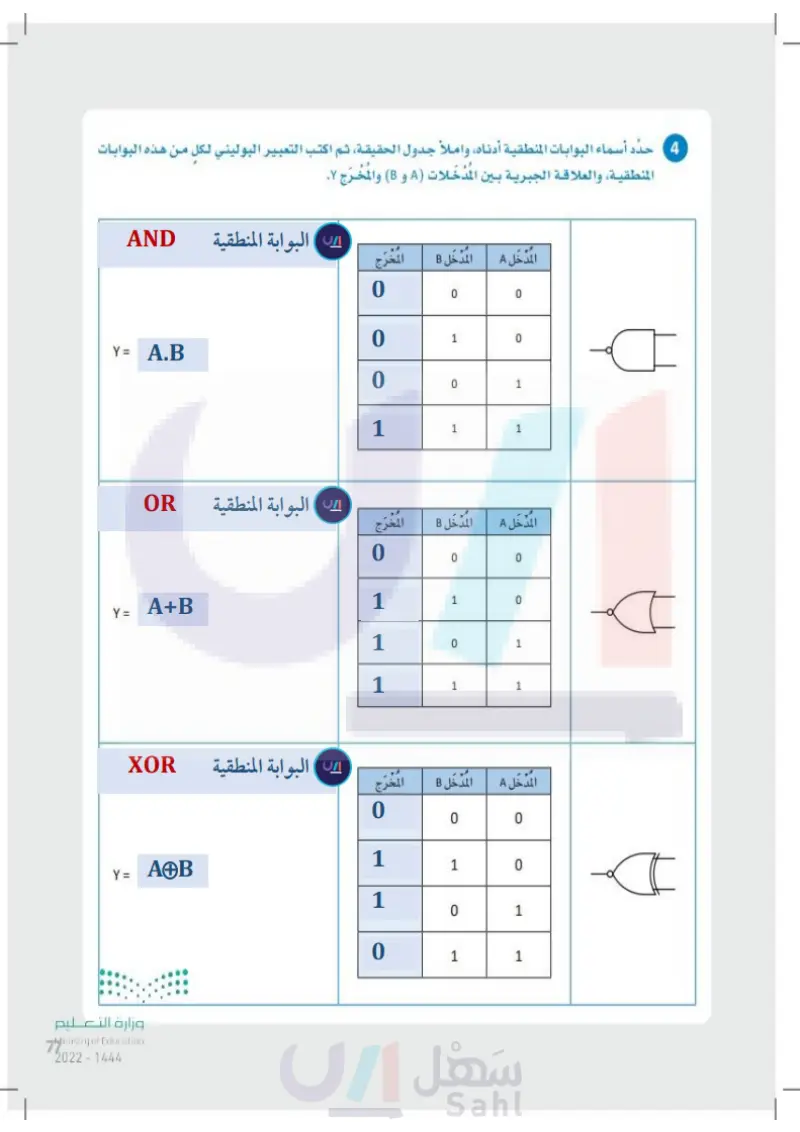
77 حدد أسماء البوابات المنطقية أدناه، واملأ جدول الحقيقة، ثم اكتب التعبير البوليني لكل من هذه البوابات المنطقية، والعلاقة الجبرية بين المدخلات A و B) والمُخْرَج ۷ . وزارة التعليم Ministry of Education 2024-1446 ۷ = Y= Y= المدخل B المدخل A الخرج 0 0 1 0 0 1 1 1 المدخل A المدخل B المخرج 0 0 1 0 0 1 1 1 المدخل B المدخل A المُخْرَج 0 0 1 0 0 1 1 1 4

حدد أسماء البوابات المنطقية أدناه واملأ جدول الحقيقة ثم اكتب التعبير البوليني لكل من هذه البوابات المنطقية
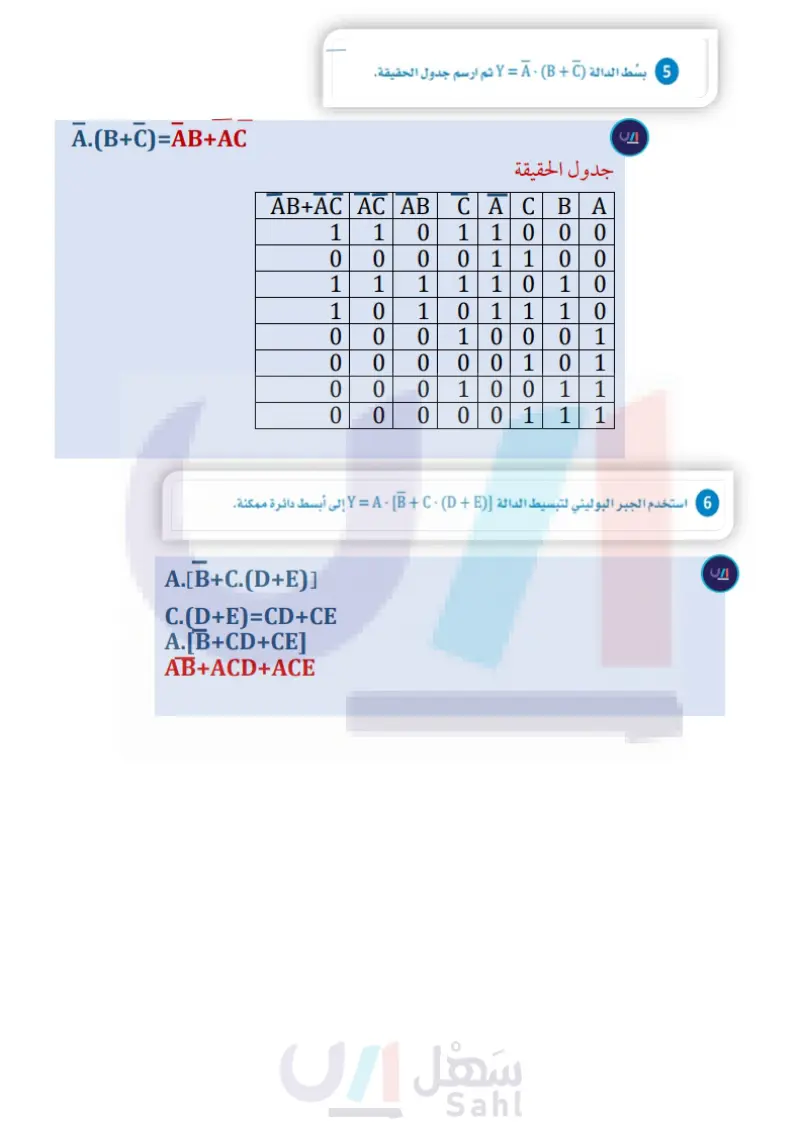
وزارة التعليم Ministry of Education 2024-1446 5 بسط الدالة A B C ، ثم ارسم جدول الحقيقة. • استخدم الجبر البوليني لتبسيط الدالة Y = A B C D E إلى أبسط دائرة ممكنة. . استخدم الدالة Y = A B + A - B لرسم الدائرة من مُخْرَجاتِها إِلى مُدْخَلاتها. OR Y=A.B+A.B 6 7 78

بسط الدالة ثم ارسم جدول الحقيقة
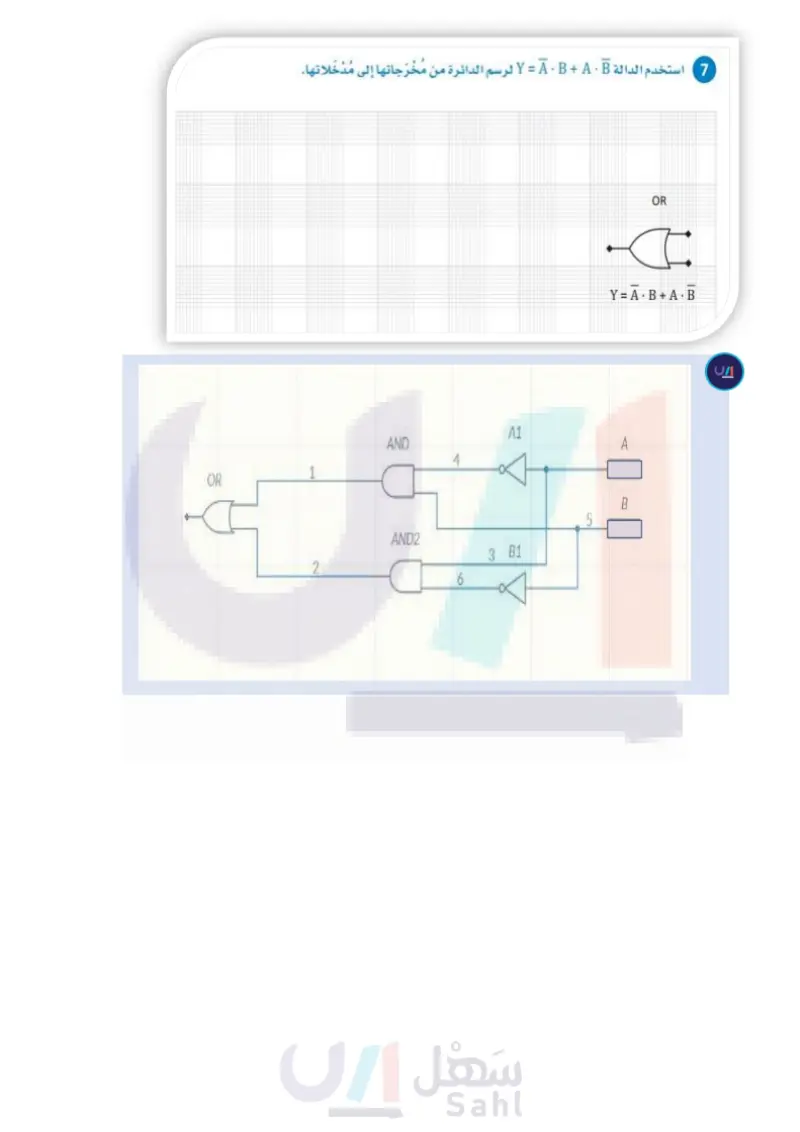
استخدم الدالة لرسم الدائرة من مخرجاتها إلى مدخلاتها
استخدم الجبر البوليني لتبسط الدالة إلى أبسط دائرة ممكنة
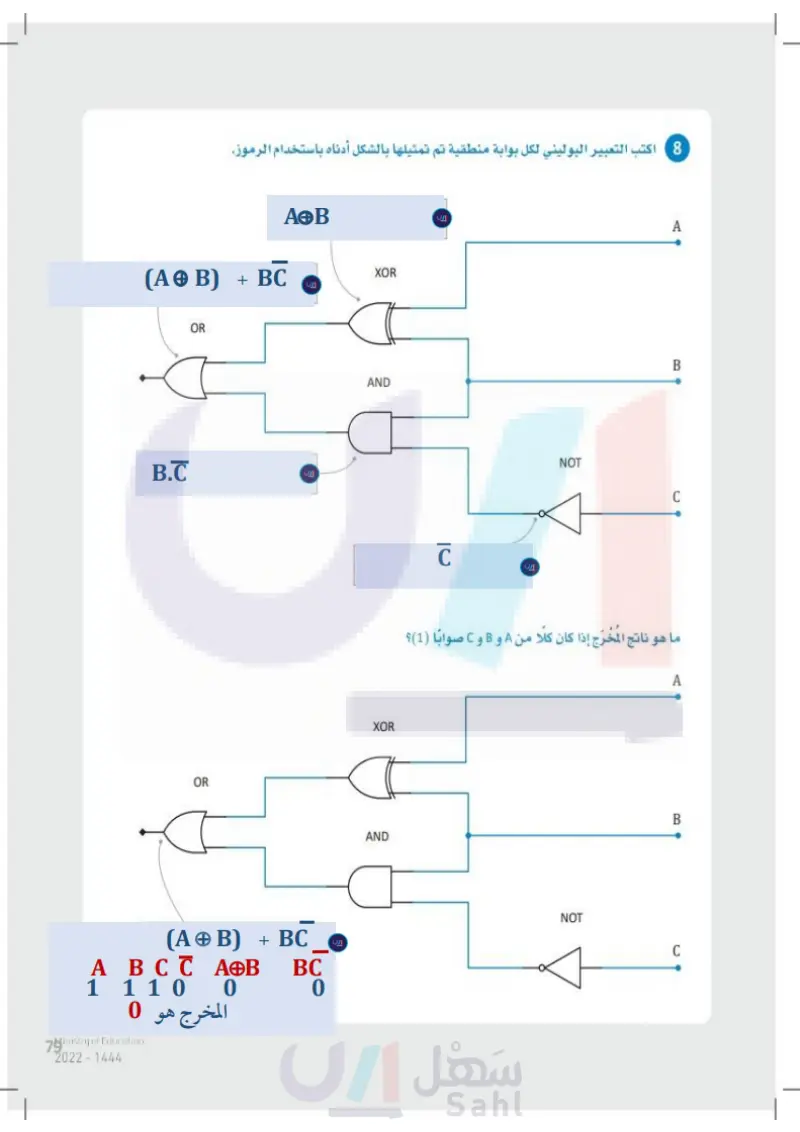
79 OR اكتب التعبير البوليني لكل بوابة منطقية تم تمثيلها بالشكل أدناه باستخدام الرموز. وزارة التعليم Ministry of Education 2024-1446 OR XOR AND XOR AND 00 8 A B NOT C ما ناتج المُخْرَج إذا كان كلُّ من A و B و C صوابا (1)؟ A B NOT C

اكتب التعبير البوليني لكل بوابة منطقية تم تمثيلها بالشكل أدناه باستخدام الرموز