قسمة كثيرات الحدود - رياضيات2-1 - ثاني ثانوي

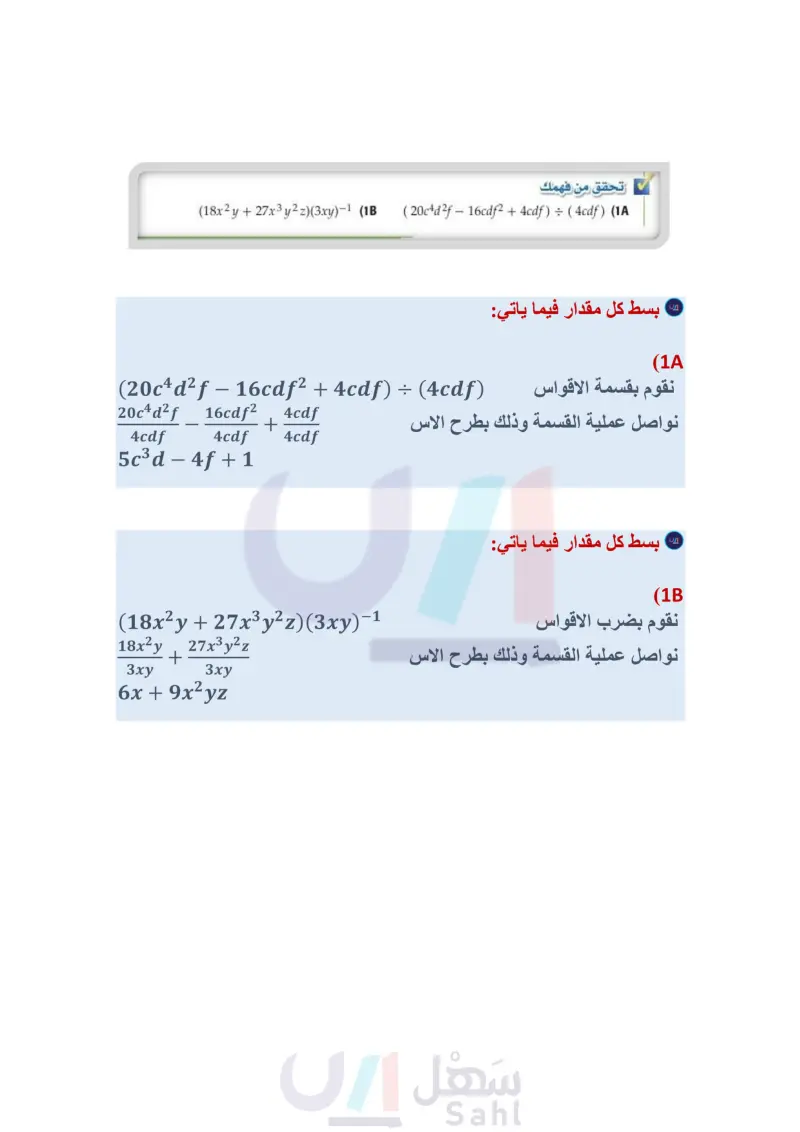
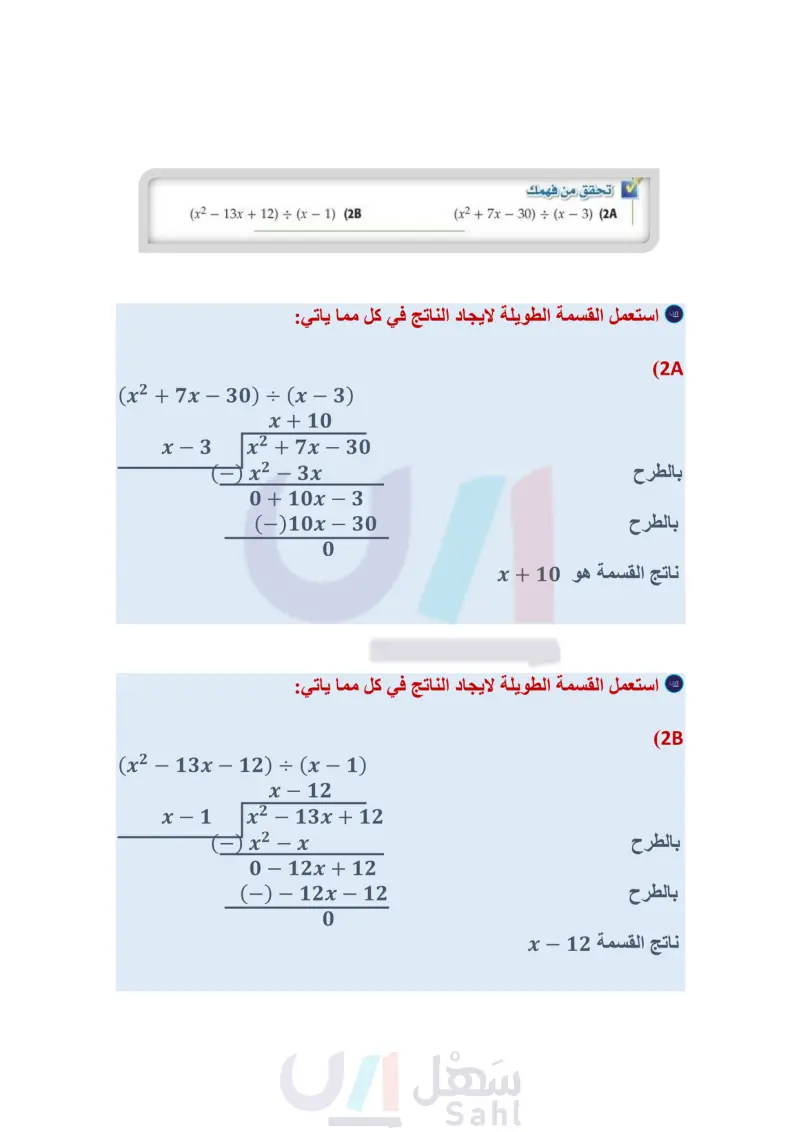
3-4 قسمة كثيرات الحدود Dividing Polynomials رابط الدرس الرقمي www.ien.edu.sa فيما سبق: درست قسمة وحيدات الحد. (الدرس (3-3) والآن لماذا؟ تحتاج سلمى إلى (140x 2 + 60x بوصة مربعة من الورق لعمل غلاف لكتاب طوله 10x بوصات. ويظهر الشكل أدناه الجزء الذي تركته للثني على جانبي الغلاف فإذا كان عرض كعب الغلاف 2x بوصة، وعرض كل الغلاف الأمامي والخلفي 6x بوصة، فما عرض كل من جزأي الثني؟ يمكنك استعمال قسمة كثيرات الحدود لمساعدتك على إيجاد الجواب. من أقسم كثيرات الحدود مستعملا القسمة الطويلة. أقسم كثيرات الحدود مستعملا القسمة التركيبية. المفردات: القسمة التركيبية 10x f 6x 2x 6x f f = عرض الثنية القسمة الطويلة : تعلمت في الدرس (3) - 3) قسمة وحيدات الحد، لذا يمكنك قسمة كثيرة حدود على 6x4y3 + 12x3y2 - 18x2y 3xy اقسم كل حد في البسط على المقام اقسم 6x4y3 + 12x3y2 - 18x2y 6x4y3 12x3y2 3xy x4 وحيدة حد مستعملا المهارات نفسها Synthetic division مثال 1 قسمة كثيرة حدود على وحيدة حد بسط العبارة إرشادات للدراسة 18x2y 3xy 3ху Зху – + =-13-1+12.x³-1y2-118x2-11-1 y 1 - 1 = y0=1 = 2x3y2 + 4x2y - 6x تحقق من فهمك (18x2y + 27x3y²z)(3xy)-1 (1B ( 20c4d2f - 16cdf2 + 4cdf ) : ( 4cdf ) (1) خطوات خوارزمية قسمة كثيرة حدود على أخرى: - اكتب كثيرة الحدود في كل من المقسوم والمقسوم عليه، بحيث تكون حدودها مرتبة ترتيباً تنازليا درجتها. حسب - ابدأ بقسمة الحد الأول في المقسوم على الحد الأول في المقسوم عليه، وضع الإجابة في المكان المخصص لذلك. - اضرب ناتج القسمة في الخطوة السابقة في المقسوم عليه، واكتب الإجابة تحت المقسوم واطرحه من المقسوم - استمر بقسمة الحد الثاني ... إلخ، حتى تصل إلى أن يكون باقي القسمة 0، أو كثيرة حدود درجتها أقل من درجة المقسوم عليه. يمكنك استعمال عملية مشابهة للقسمة الطويلة لقسمة كثيرة حدود على كثيرة حدود أخرى. وتسمى خطواتها خوارزمية القسمة. مثال 2 قسمة كثيرة حدود على كثيرة حدود أخرى استعمل القسمة الطويلة لإيجاد ناتج (5) - (x2 + 3x - 40 : (x) . x + 8 5/x2+3x-40 x2 - 5x 8x - 40 (-) 8x - 40 0 X ― ناتج القسمة هو 8 + x، والباقي 0. تحقق من فهمك (x2+7x30) (x-3) (2A اضرب المقسوم عليه في X اطرح اضرب المقسوم عليه في 8 اطرح (x2 - 13x + 12) : (x - 1) (2B وزارة التعليم Ministry of Education الدرس -4-3 قسمة كثيرات الحدود 213114

قد ينتج باقٍ عن قسمة كثيرتي حدود كما في قسمة الأعداد الكلية، فمثلا عند إيجاد 3 : 11 يكون الناتج 3 والباقي ،2، وتكتب عادةً على الصورة 3. ويمكنك كتابة نتيجة قسمة كثيرتي حدود مع باق بالطريقة نفسها. مثال 3 على اختبار 132 أي مما يأتي يكافئ العبارة: a2 + 7a - 11)(3 - a1) ؟ -a - 10+ -a-10. 3 19 - 19 3- - a a C D a + 10 - 3. 19 ― a A -a+10 B اقرأ فقرة الاختبار إرشادات للدراسة الاختيار من متعدد يمكنك حذف بعض البدائل عن طريق اختيار قيمة للمتغير 1 ثم تعويض هذه القيمة في العبارة الأصلية وفي البدائل وإيجاد قيمة كل منها. بما أن العامل الثاني مرفوع للأس -1-، فهذه إذن مسألة قسمة. - (a27a 11)(3 - a)-1= a2 + 7a - 11 3 a حل فقرة الاختبار لتسهيل عملية القسمة، أعد كتابة a - 3 على الصورة 3 + a- -a-a + (3) = a2 - 3a 7a-(-3a)=10a -10(-a+3)= 10a - 30 -11 (-30) 19 -11-(-30) = -a - 10 -a + 3/a² + 7a 11 (-) a2 – 3a 10a 11 (-) 10a-30 19 ناتج القسمة هو 10 - a، والباقي 19 · لذا فإن 10+ 19 - a 3 + 10 - a - = 1- ( - 3)(11) - (2) ، ومن ثم تكون الإجابة هي البديل .C. تحقق من فهمك ― (3) أي مما يأتي يكافئ العبارة: 1- (2 - 1)(7 + 5 + 2)؟ r - 6+ 1 13 ― r C r+6 13 1. D - r 13 +9-1- 6 A 1 r +6 B القسمة التركيبية : القسمة التركيبية هي طريقة مبسطة لقسمة كثيرة حدود على ثنائية حد. مفهوم أساسي القسمة التركيبية أضف إلى مطويتك الخطوة 1: اكتب معاملات المقسوم بعد ترتيب حدوده تنازليا بحسب درجتها. تأكد من أن المقسوم عليه على الصورة X ، ثم اكتب الثابت T في الصندوق، واكتب المعامل الأول أسفل الخط الأفقي. الخطوة 2 : اضرب المعامل الأول في ، واكتب الناتج أسفل المعامل الذي يليه. الخطوة 3 : اجمع ناتج الضرب مع المعامل الذي فوقه. ' الخطوة 4: كرر الخطوتين 2 على ناتج الجمع في الخطوة السابقة حتى تصل إلى ناتج جمع العددين في العمود الأخير. الأعداد في الصف الأخير تمثل معاملات ناتج القسمة ودرجة الحد الأول أقل بواحد من درجة المقسوم والعدد الأخير هو الباقي. وزارة التعليم Ministry of Education 2024-1446 الفصل 3 كثيرات الحدود ودوالها 132

42 -13 26 -24 ↓ 2 42-13 مثال 4 القسمة التركيبية تنبيه القسمة التركيبية تذكر أن الحدود تجمع ولا تطرح عند إجراء القسمة التركيبية. استعمل القسمة التركيبية؛ لإيجاد ناتج (4) - 2x3 - 13x2 + 26x - 24 : (x) . الخطوة 1: اكتب معاملات المقسوم واكتب الثابت r في الصندوق، وهو في هذا المثال .4 ثم اكتب المعامل الأول وهو 2 أسفل الخط الأفقي. الخطوة 2: اضرب المعامل الأول في الثابت: 8 = (4) 2 ، واكتب الناتج أسفل المعامل الثاني. الخطوة 3 : اجمع ناتج الضرب مع المعامل الثاني: 26 -24 8 2 42 26 -13 -24 8 2 -5 | 42 26 -13 -24 8 -20 24 2 -5/6/0 -13+8=-5 إرشادات للدراسة القسمة التركيبية الخطوة 4: اضرب المجموع وهو 5- في الثابت : 20 = 4 × 5 ، واكتب الناتج أسفل المعامل التالي، ثم اجمع: 6=(2620 . اضرب المجموع وهو 6 في الثابت r: 24 = (4) 6 ، واكتب ناتج الضرب تحت المعامل التالي، إذا لم يوجد أحد الحدود في كثيرة حدود المقسوم ثم اجمع : 0 = 24 + 24 . فأضفه وليكن معامله صفرًا. فمثلا إذا كان إذن ناتج القسمة هو 6 + 2x2 - 5x، والباقي 0. 2x2 5x + 6 (x) X 4 - 24 8x2 + 20x (+) 2x³- 5x² + 6x 2x313x²+26x-24 وزارة التعليم Ministry of Education الدرس -4-3 قسمة كثيرات الحدود 213314 تحقق اضرب ناتج القسمة في المقسوم عليه، فيكون الناتج هو المقسوم. تحقق من فهمك (2x3 + 3x²-4x+15) ÷ (x+3) (4A (3x38x2+11x-14) ÷ (x-2) (4B 14)(x2) (4a42a24a+12) ÷ (a + 2) (4C (6b48b3+12b-14) ÷ (b-2) (4D المقسوم 2x3 – 4x2 +6 فاكتبه في صورة 2x3 - 4x2 +0x+6

عليه ولإجراء القسمة التركيبية يجب أن يكون المقسوم عليه على الصورة x - r، وإذا كان معامل x في المقسوم لا يساوي الواحد، فيجب إعادة كتابة عبارة القسمة بحيث يمكنك استعمال القسمة التركيبية. مثال 5 معامل x في المقسوم عليه لا يساوي 1 استعمل القسمة التركيبية؛ لإيجاد ناتج : 1 + 3x4 - 5x3 + x2 + 7x ) : (3x ) . أعد كتابة العبارة ليكون معامل x في المقسوم عليه 1 وذلك بقسمة كل من البسط والمقام على 3. بسط كلا من البسط والمقام 3x4. 5x3 + x2 + 7x 3x + 1 3x4 - 5x3 + x2 + 7x) : 3 (3x + 1) ÷ 3 x4 5 + X2 + 7. -x 3" x + 1 3 وبما أن المقسوم لا يحتوي حدا ثابتًا، فضع صفرًا مكانه. 1 5 1 7 x-r=x+ r = 1 0 3 3 3 3 3 2 -1- 3 - 3 1 2 3 1 -2 1 2-2 3 - 2 + x 3 - 2x 2 + x . وأخيرًا بسّط الكسر اضرب كلا من البسط والمقام في العدد ] بسط 23 x + وعليه فإن الناتج هو . 23 X + || = 23 3 x 3x(x + 2 3x + 1 وعليه يكون الناتج هو : 1 2 3 3x+1 . x3 - 2x2 + x + 2 . تحقق أوجد ناتج القسمة مستعملاً القسمة الطويلة. x3 - 2x2 + x + 2 3x + 1 / 3x4 – 5x3 + x2 + 7x (-) 3x + x³ x3 -6x3 + x²+7x (-) -6x³- 2x² 3x2 + 7x . x3 - 2x 2 + x + 2 - 3x2 + x 6x 6x + 2 -2 تنبية! قسمة جميع الحدود تذكر أن تقسم جميع الحدود في البسط والمقام على معامل X في المقام. 2 وعليه يكون الناتج هو 1 + 3x تحقق من فهمك - (8y5 — 2y¹ — 16y² + 4) ÷ (4y − 1) (5B - - (6c3 17c2+6c+8) ÷ (3c-4) (5D (8x4 - 4x2 + x + (4) ÷ (2x + 1) (5 (15b38b2-21b+6) ÷ (5b-4) (5C وزارة التعليم Ministry of Education 2024-1446 الفصل 3 كثيرات الحدود ودوالها 134

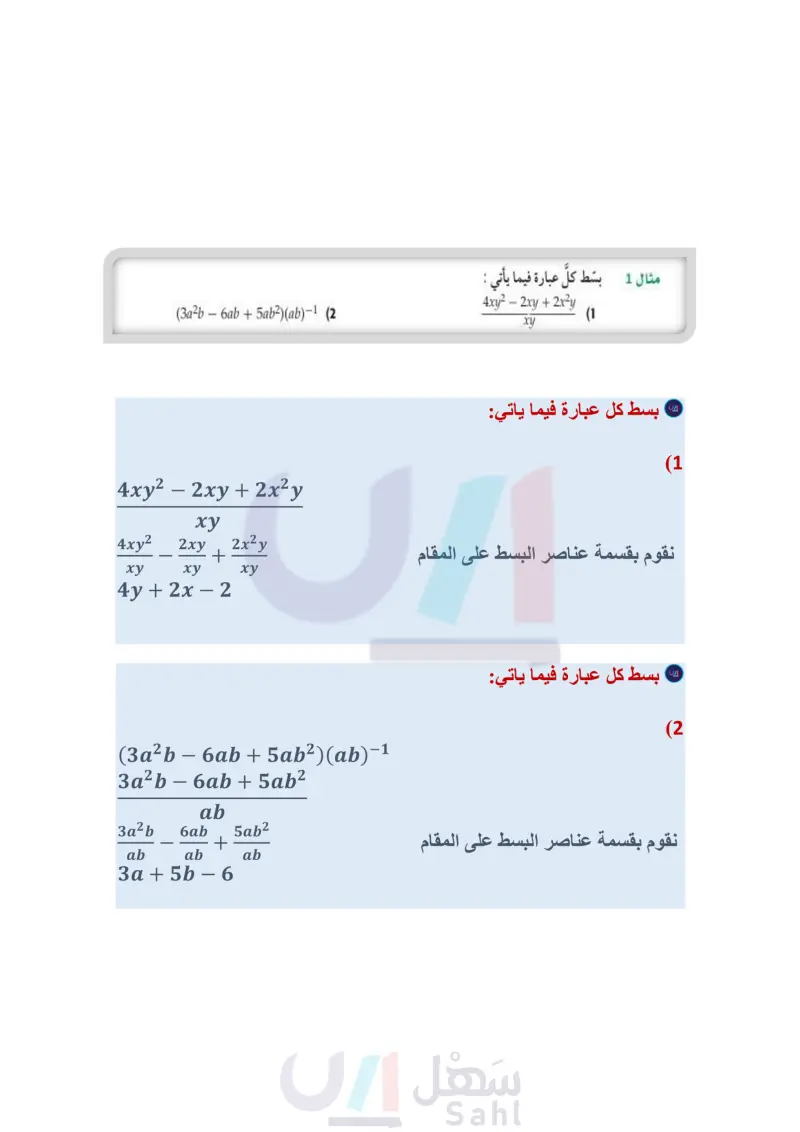
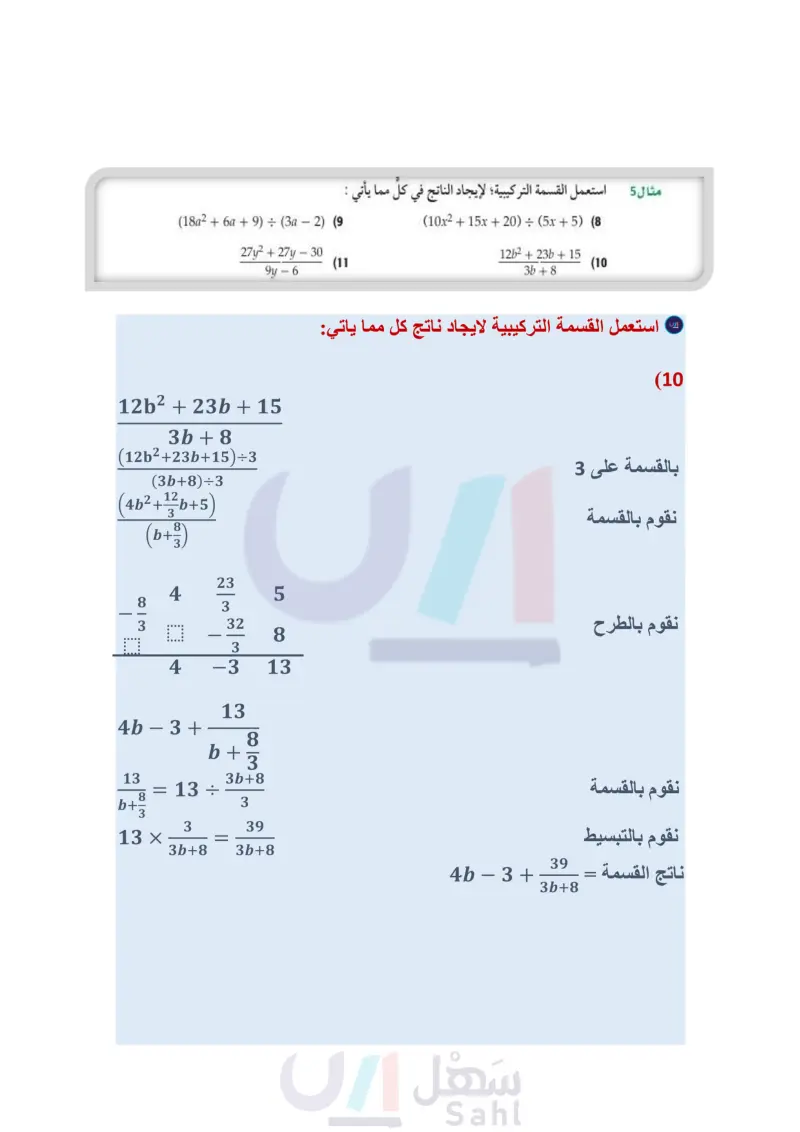
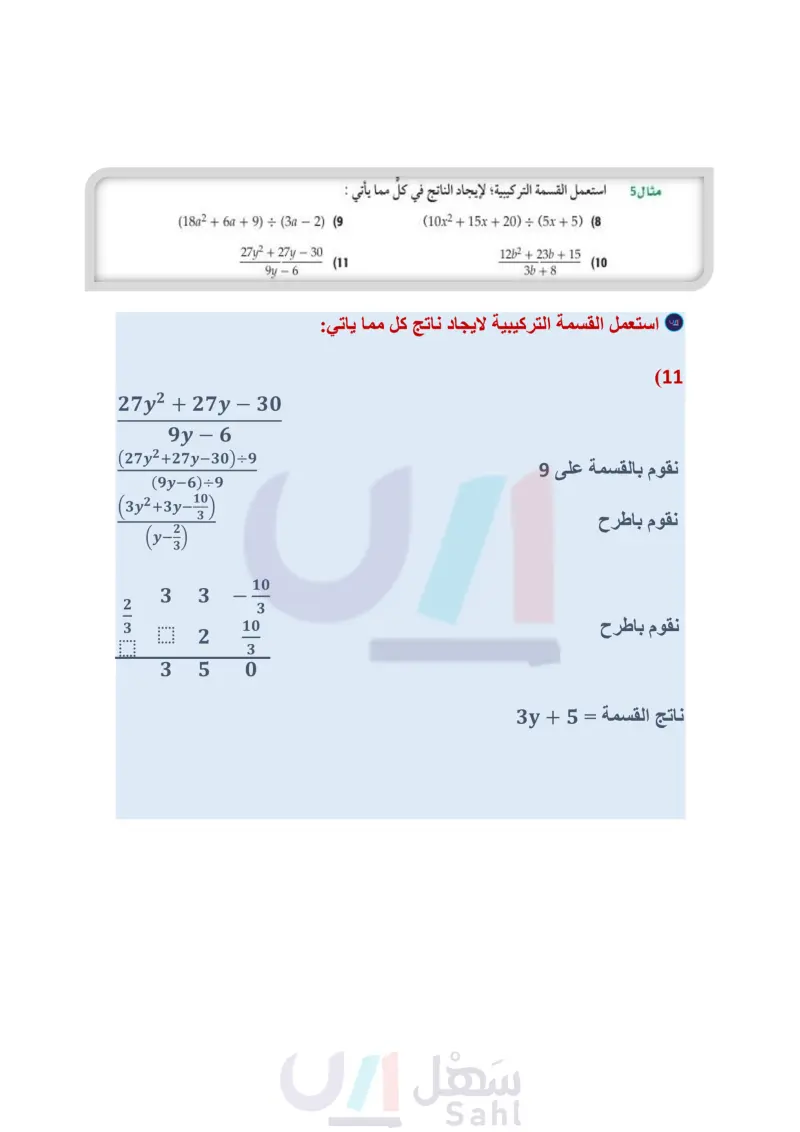
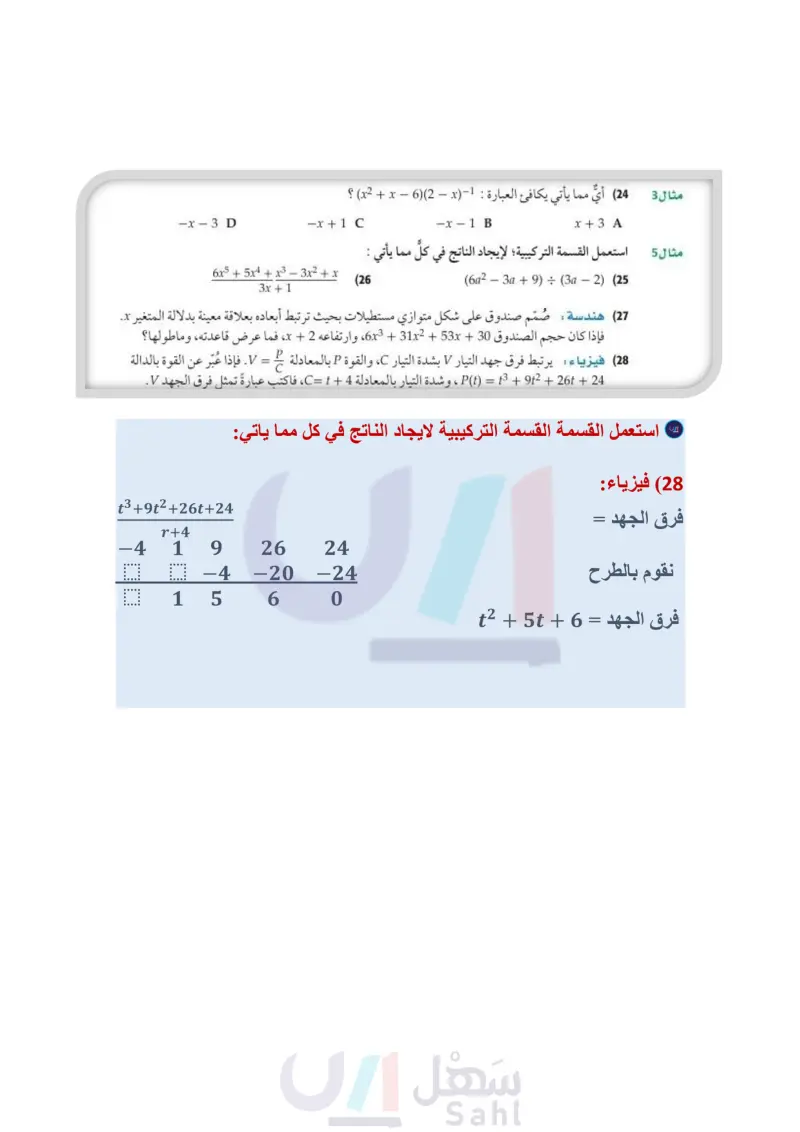
تأكد بسط كلَّ عبارة فيما يأتي : مثال 1 4xy2 - 2xy + 2x2y (1 xy (3a2b6ab5ab²)(ab)-1 (2 استعمل القسمة الطويلة (خوارزمية القسمة أو القسمة التركيبية؛ لإيجاد الناتج في كل مما يأتي: المثالان 24 (202 - 40 - (8) : (a + (1) (4) (y5-3y²-20)(y-2) (6 (x²-6x-20) ÷ (x+2) (3 (3z4-6z3-9z2 + 3z − 6) ÷ (z + 3) (5 - (7) اختيار من متعدد: أي مما يأتي يكافئ العبارة : 1- (x2 + 3x - 9)(4 - x) ؟ مثال 3 - x - 7 B - x - 7 + 19 4 X A 19 -x-7-- 19 D x + 7 - . C 4. X X استعمل القسمة التركيبية؛ لإيجاد الناتج في كل مما يأتي : مثال 5 (18a26a+9) ÷ (3a 2) (9 ― 27y2 + 27y - 30 9y - 6 (11 (10x215x+20) ÷ (5x+5) (8 1262 +23b+ 15 3b+8 (10 تدرب وحل المسائل مثال 1 بسط كل عبارة فيما يأتي : 7g³h² + 3g²h − 2gh³ gh - (14 9n3p3 – 18n2p2 + 21n2p3 (17 3n2p2 5x2y - 10xy + 15xy2 5xy 16c4d4 – 24c2d2 402d2 24a3b2 - 16a2b3 (13 (12 8ab 4a3b – 6ab + 2ab2 (16 (15 2ab استعمل القسمة الطويلة (خوارزمية القسمة) أو القسمة التركيبية؛ لإيجاد الناتج في كل مما يأتي: المثالان 24 (b34b2b-2) ÷ (b+1) (19 (x5 - 4x³ + 4x²) ÷ (x − 4) (21 (84 – 3g² – 18) ÷ (g − 2) (23 - (a28a26) (a + 2) (18 (z4 - 3z3 + 2x² - 4z + 4)(z − 1)−1 (20 - y3 + 11y2 – 10y + 6 y+2 (22 (24) أيُّ مما يأتي يكافئ العبارة : 1- (x2 + x - 6) (2 - x) ؟ مثال 3 x + 3 A - x - 1 B - x - 3D -x + 1 C استعمل القسمة التركيبية؛ لإيجاد الناتج في كل مما يأتي : مثال 5 - (6a² − 3a + 9) ÷ (3a - 2) (25 فإذا كان حجم (26 6x5 + 5x4 + x3 - 3x2 + x 3x + 1 (27) هندسة : صُمّم صندوق على شكل متوازي مستطيلات بحيث ترتبط أبعاده بعلاقة معينة بدلالة المتغير x . الصندوق 30 + 6x3 + 31x 2 + x، وارتفاعه 2 + x ، فما عرض قاعدته، وماطولها؟ (28 فيزياء يرتبط فرق جهد التيار V بشدة التيار ، والقوة P بالمعادلة = v . فإذا عُبّر عن القوة بالدالة C، } : 24 + P( = t3 + 92 + 26t) ، وشدة التيار بالمعادلة 4 + ، فاكتب عبارةً تمثل فرق الجهد .V . C بسط كلَّ عبارة فيما يأتي: (a3b2a2b+2b)(ab) (31 (28c³d² - 21cd²) ÷ (14cd) (30 5 + 2 + 524 لاقي والتعليم Ministry of Educatiz+2 (34 p3 + 2p2 – 7p – 21 (33 p + 3 (x4 — y¹) ÷ (x − y) (29 n33n25n-4 n + 4 (32 الدرس -4-3 قسمة كثيرات الحدود 14 2135

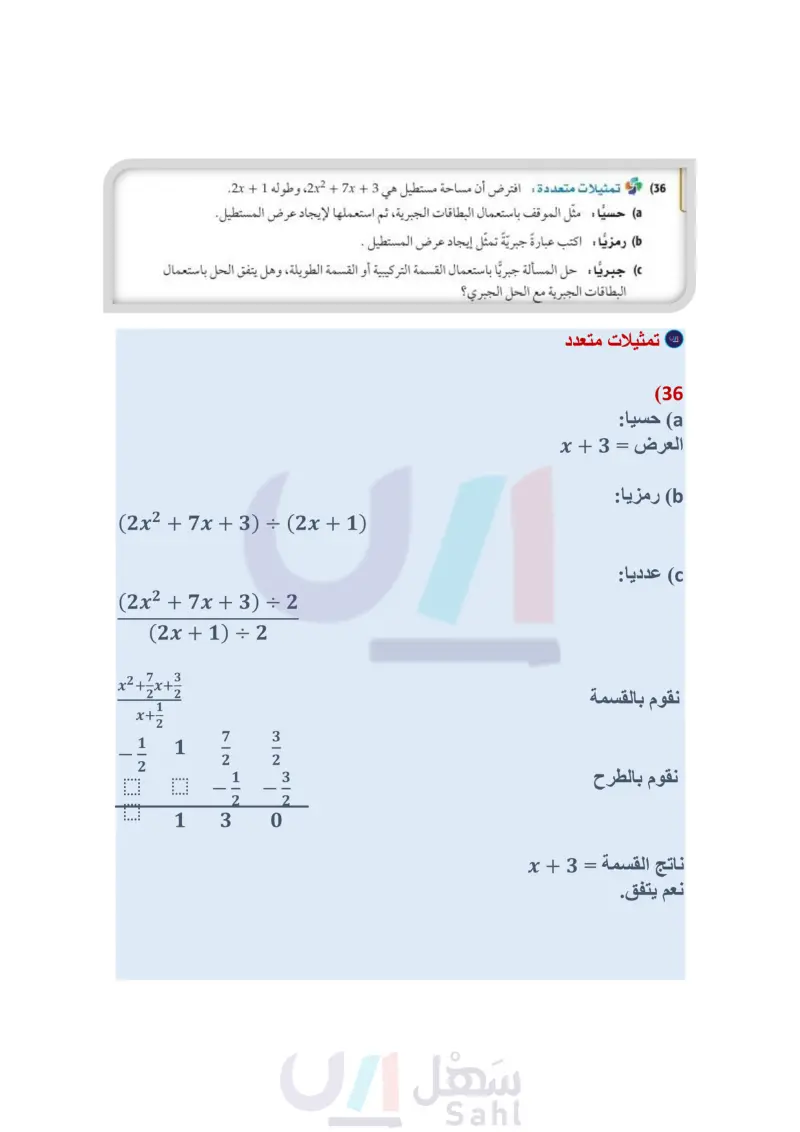
هل اتعلم؟ أن ترك الحنفية مفتوحة أثناء تتغليف الأسنان يهدر أكثر من ١٥ الترا من المياه الصالحة للشرب والمارة المياه والكهرباء الارشيد طاعة الله الربط مع الحياة فن الإعلان جزء من النشاط الترويجي المتعدد العناصر، ولكنه يتفوق من حيث إمكانية تحقيقه اتصالا على نطاق واسع جدًا في وقت محدود. ومع التطور التقني تطوّر تصميم وإخراج الدعاية والإعلانات. ومن أنواع الإعلانات: الإعلان المطبوع، الخارجي، الإعلان المسموع 3500a² a2 + 100 = n ؛ حيث a المبلغ (35) أعمال يمكن تقدير عدد النسخ المبيعة من مجلة باستعمال المعادلة الذي تنفقه المجلة على الإعلان بمئات الريالات، و n عدد النسخ المبيعة من المجلة. a أجر عملية القسمة المعبر عنها بالمقدار: 3500a² a2 + 100 كم نسخة بيعت من المجلة إذا أُنفق على الدعاية والإعلان 6000 ريال؟ (36) تمثيلات متعددة : افترض أن مساحة مستطيل هي 3 + 2x2 + x، وطوله 1 + 2x. a حسيًّا : مثل الموقف باستعمال البطاقات الجبرية، ثم استعملها لإيجاد عرض المستطيل. (b) رمزيًا : اكتب عبارةً جبريةً تمثل إيجاد عرض المستطيل . ( جبريًا : حل المسألة جبريًا باستعمال القسمة التركيبية أو القسمة الطويلة، وهل يتفق الحل باستعمال البطاقات الجبرية مع الحل الجبري ؟ مسائل مهارات التفكير العليا (37) اكتشف الخطأ : قسَّم كلّ من خليفة وجمال 1 - 2x3 - 4x 2 + x على 3 - x ، فقال خليفة: إن الباقي 26، وقال جمال: إن الباقي 100 فأيهما إجابته صحيحة ؟ فسّر إجابتك. الإعلان المباشر، الإعلان (38) تحد : إذا قسمت كثيرة حدود على ثنائية حد وكان الباقي ، فما الذي تستنتجه عن العلاقة بينهما؟ المرئي، الإعلان التفاعلي (39) تبرير راجع أحد أسئلة القسمة في هذا الدرس، وبيّن العلاقة بين درجة كل من: المقسوم، والمقسوم عليه، وناتج القسمة. (40) مسألة مفتوحة : اكتب عبارة تتضمن قسمة كثيرتي حدود ، بحيث يكون الباقي 3 . (41) حدد العبارة المختلفة عن العبارات الثلاث الأخرى، وفسّر إجابتك. 3xy + 6x2 5% x2 x +5 5b + 110 – 9ad 2 (42) اكتب: استعن بالمعلومات المعطاة في فقرة "لماذا؟" في بداية هذا الدرس ، واكتب تعليمات متسلسلة لعمل غلاف لكتاب الرياضيات باستعمال قسمة كثيرات الحدود. (44) أي كثيرات الحدود الآتية درجتها 3؟ تدريب على اختبار (43) أي مما يأتي يكافئ العبارة: (1 + 4x2 + 2x + 3 - 3(2x2 - 5x)؟ x2 + x + 123 x3 + x2 - 2x4 1 + x + x3 D - 2x2 - 3x + 4 B -10x²+17x C 2x2 + 17x D وزارة التعليم Ministry of Education 2024-1446 (3ab2)-2(2a2b)2 (47 h(2b+1) (51 2x2 A -10x2 B مراجعة تراكمية بسط كلَّ عبارة فيما يأتي : (الدرس (3-3) 4a(2a3)+3a(5a-4) (45 (xy)²(2xy²z)³ (46 إذا كان 3 + x) = - 22 - 2x + 14, f(x) = 4x) ، فأوجد قيمة كل مما يأتي: (الدرس (2-1) f(c) (50 h(3) (49 f(-6) (48 136 الفصل 3 كثيرات الحدود ودوالها