العمليات على كثيرات الحدود - رياضيات2-1 - ثاني ثانوي

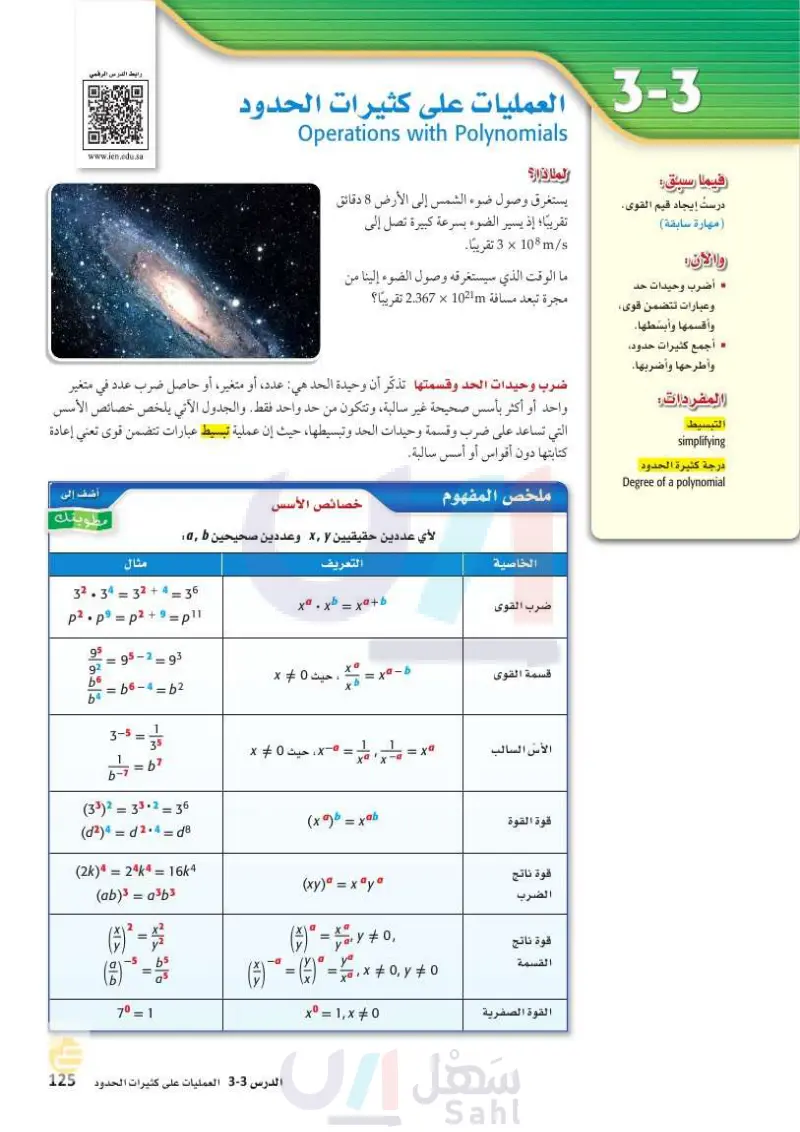
33 العمليات على كثيرات الحدود رابط الدرس الرقمي Operations with Polynomials www.ien.edu.sa فيما سبق: درستُ إيجاد قيم القوى . (مهارة سابقة) والآن أضرب وحيدات حد وعبارات تتضمن قوى، وأقسمها وأبسطها. أجمع كثيرات حدود، وأطرحها وأضربها. المفردات التبسيط simplifying لماذا؟ يستغرق وصول ضوء الشمس إلى الأرض 8 دقائق تقريبًا؛ إذ يسير الضوء بسرعة كبيرة تصل إلى m/s 108 × 3 تقريباً. ما الوقت الذي سيستغرقه وصول الضوء إلينا من مجرة تبعد مسافة 1021m × 2.367 تقريبًا؟ ضرب وحيدات الحد وقسمتها تذكر أن وحيدة الحد هي: عدد، أو متغير، أو حاصل ضرب عدد في متغير واحد أو أكثر بأسس صحيحة غير سالبة، وتتكون من حد واحد فقط. والجدول الآتي يلخص خصائص الأسس التي تساعد على ضرب وقسمة وحيدات الحد وتبسيطها، حيث إن عملية تبسيط عبارات تتضمن قوى تعني إعادة كتابتها دون أقواس أو أسس سالبة. درجة كثيرة الحدود Degree of a polynomial ملخص المفهوم الخاصية ضرب القوى قسمة القوى الأس السالب قوة القوة قوة ناتج الضرب قوة ناتج القسمة القوة الصفرية خصائص الأسس لأي عددين حقيقيين ، وعددين صحيحين ab التعريف مثال أضف إلى مطويتك 32.34 = 32 + 4 = 36 xa . xb = xa + b = xa - b X ، حيث 0 ≠ x p2. p9 = p2 + 9 = pil b4 قافةاة 95 = 95-293 92 b6 = b6 - 4 = b2 3-5 1 = 35 1 xa ، حيث 0 ≠ x b7 1 1 = ' = xa X b (33)² = 33.2 = 36 (2)4 = d2.4 = d8 (xg) b = xab (2k)4 = 24k4 = 16k4 (ab)3 = a3b3 (xy)° = x°y ° a = y = 0, y ya (+) = ( 4 ) = x + 0, y #0 ' x₁₁ x0 = 1,x#0 b5 = = N 70 = 1 ماه وزارة التعليم Ministry of Education الدرس 3- العمليات على كثيرات الحدود 14 2125

إرشادات للدراسة تحقق يمكنك التحقق من إجابتك دائما باستعمال تعريف الأسس، فمثلا: = 9.9 ۹۰۹۰۹۰۹۰۹۰۹۰۹ 1 95 126 عند تبسيط وحيدة الحد، تأكد من أنك قد كتبتها في أبسط صورة. مفهوم أساسي تبسيط وحيدات الحد تكون وحيدة الحد في أبسط صورة عندما: لا تتضمن قوى قوة. . يظهر كل أساس مرة واحدة. . تكون جميع الكسور المتضمنة في أبسط صورة. . لا تتضمن أقواسًا أو أسسا سالبة. أضف إلى مطويتك مثال 1 تبسيط العبارات بسط كل عبارة فيما يأتي مفترضًا أن أيَّا من المتغيرات لا يساوي صفرًا: (2a-2)(3a3b2)(c-2) (a (2a-2)(3a3b2)(c-2) = 6ab2 c-2 = bab² ( 1121 ) 9214 (b 6ab2 c2 9713 92-7.14-3 9214 9773 = = 9-5 r r -2a4 3 b2 (c -2a43 b2 (-2a4)3 = = (62) 3 (-2)3(a4)3 (62)3 -8912 66 تحقق من فهمك (2x-3y³)(-7x5y-6) (1A (1C الفصل 3 كثيرات الحدود ودوالها قسمة القوى اضرب 2 في 3 ، واضرب 2-a في a3 تعريف الأسس السالبة بسط اطرح الأسس تعريف الأسس السالبة قوة ناتج القسمة قوة ناتج الضرب قوة القوة 15c5d3 -3c2d7 (1B (-2x 3y2)5 (1D وزارة التعليم Ministry of Education 2024-1446

إرشادات للدراسة كثيرات الحدود تذكر أن كثيرة الحدود هي وحيدة حد أو مجموع العمليات على كثيرات الحدود: درجة كثيرة الحدود المبسّطة هي أكبر درجة لوحيدات الحد المكونة لها. فمثلا درجة كثيرة الحدود 58 + 4x + x2 هي. .2 مثال 2 درجة كثيرة الحدود وحيدات حد، وتُسمى كل حدد ما إذا كانت كل عبارة فيما يأتي كثيرة حدود أم لا، وإن كانت كذلك فاذكر درجتها: وحيدة حد منها حدا في كثيرة الحدود ودرجة وحيدة الحد هي مجموع أسس كل متغيراتها. - 1x4y³ – 8x5 (a تعدّ هذه العبارة كثيرة حدود؛ لأن كل حد فيها هو وحيدة حد؛ ودرجة الحد الأول فيها تساوي 7 = 3 + 4، ودرجة الحد الثاني 5؛ لذا فإن درجة كثيرة الحدود 7. VT + x + 4 (b هذه العبارة ليست كثيرة حدود؛ لأن V ليست وحيدة حد. x-3+2x-2+6 (c هذه العبارة ليست كثيرة حدود؛ لأن كلا من: x3 x2 ليست وحيدة حد؛ حيث X 1 1 = X = تحقق من فهمك x3 3-x ، ووحيدات الحد لا تتضمن متغيرات في المقام. x5y + 9x4y3 - 2xy (28 x + 3x2 (2 y إرشادات للدراسة طرائق بديلة لا حظ أن المثال 30 يستعمل طريقة الجمع الأفقي. على حين يستعمل المثال 36 طريقة الجمع الرأسي وكلتاهما تؤدي إلى الإجابة الصحيحة. يمكنك إجراء العمليات المطلوبة على كثيرات الحدود وتبسيطها تمامًا كما تبسّط وحيدة الحد، ثم تجمع الحدود المتشابهة. مثال 3 جمع كثيرات الحدود وطرحها أوجد ناتج كل مما يأتي، واكتبه في أبسط صورة: (4x2 - 5x + 6) - (2x2 + 3x - 1) (a تخلّص من الأقواس وجمع الحدود المتشابهة. (4x2 - 5x + 6 - (2x2 + 3x - 1) . = 4x2 – 5x + 6 - 2x2 - 3x + 1 = (4x² - 2x²) + (-5x-3x) + (6+1) = 2x2 - 8x + 7 (6x2 - 7x + 8) + (-4x2 + 9x - 5) (b العبارة الأصلية وزّع العدد 1- جمع الحدود المتشابهة اجمع الحدود المتشابهة وزارة التعليم Ministry of Education رتب الحدود المتشابهة رأسيًا، وأوجد ناتج الجمع. 6x2 - 7x + 8 (+)-4x²+9x - 5 2x2 + 2x + 3 تحقق من فهمك (3x2. 6)+(-x+1) (3B (-x² - 3x + 4) - (x² + 2x+5) (3A الدرس 3- العمليات على كثيرات الحدود 2127144

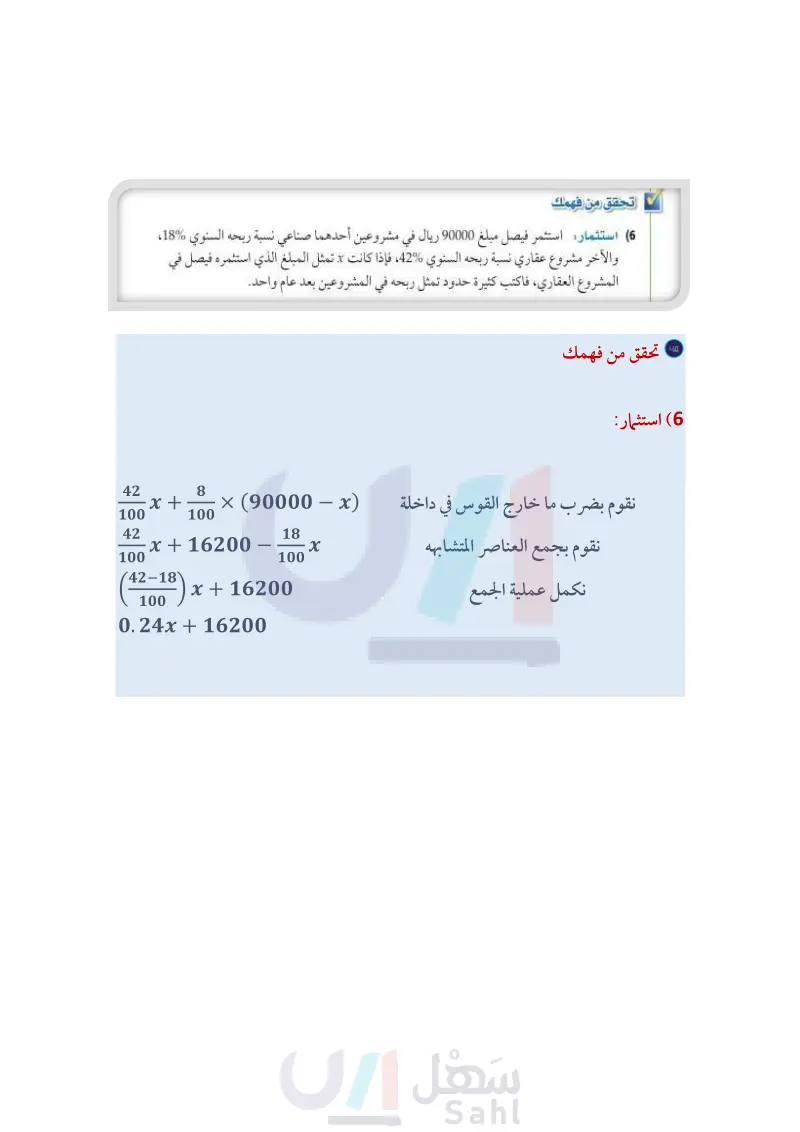
يمكنك استعمال خاصية التوزيع لضرب كثيرات الحدود. مثال 4 ضرب وحيدة حد في كثيرة حدود أوجد ناتج (6) - 4 - 3x (2x2، واكتبه في أبسط صورة. 3x(2x²-4x+6) = 3x(2x²) + 3x(-4x)+ 3x(6) = 6x3 - 12x2 + 18x خاصية التوزيع اضرب في وحيدة الحد تحقق من فهمك x2(6x2 + 9x - 12) (4A - -2a(-3a² 11a +20) (4B مثال 5 ضرب كثيرات الحدود أوجد ناتج : 2 + 6 - 4 (2)، واكتبه في أبسط صورة. (2) + 4n - 6)(n + (2) = n2(n + 2) + 4n(n + 2) + (6)(n + 2 خاصية التوزيع خاصية التوزيع = n².n+n².2+4n•n+4n•2+(-6)•n+(-6).2 = 13 + 212 + 4n2 + 8n - 6n - 12 n3 = n3 + 6n2 + 2n 12 تحقق من فهمك (x² + 4x + 16)(x - 4) (5A اضرب وحيدات الحد اجمع الحدود المتشابهة (2x24x+5)(3x-1) (5B إرشادات للدراسة قانون المسافة تذكر أن: يمكنك استعمال كثيرات الحدود لتمثيل مواقف من واقع الحياة. مثال 6 من واقع الحياة كتابة عبارة كثيرة حدود قيادة تتطلب أنظمة إحدى شركات النقل البري أن تكون مدة قيادة سائقي الشاحنات 10 ساعات يوميًّا، المسافة = السرعة الزمن تتخللها فترة استراحة، فإذا قاد أحد سائقي الشركة شاحنته في فترة ما قبل الاستراحة بسرعة 90km/h ، وبعد الاستراحة بسرعة 100km/h ، فاكتب كثيرة حدود تمثل المسافة التي قطعها التعبير اللفظي قاد السائق سيارته بسرعة 90km/h في فترة ما قبل الاستراحة ، و 100km/h في فترة ما بعد الاستراحة . المتغير ليكن X عدد ساعات القيادة قبل الاستراحة. الربط مع الحياة تعقد معظم الدول دورات تدريبية متخصصة واختبارات مشددة لقائدي الشاحنات للتأكد من مستوى تأهيلهم لقيادتها، وتوعيتهم بكيفية التعامل مع الطرق السريعة، بما يقلل المخاطر ويؤمن حركة السير. 90 x 100 (10 - x) العبارة 90x + 100(10 - x) = 90x + 1000 - 100x = 1000 – 10x فتكون كثيرة الحدود هي 10x – 1000 تحقق من فهمك خاصية التوزيع اجمع الحدود المتشابهة 6 استثمار استثمر فيصل مبلغ 90000 ريال في مشروعين أحدهما صناعي نسبة ربحه السنوي %18، والآخر مشروع عقاري نسبة ربحه السنوي ،42، فإذا كانت x تمثل المبلغ الذي استثمره فيصل في المشروع العقاري، فاكتب كثيرة حدود تمثل ربحه في المشروعين بعد عام واحد وزارة التعليم 128 الفصل 3 كثيرات الحدود ودوالها Ministry of Education 2024-1446

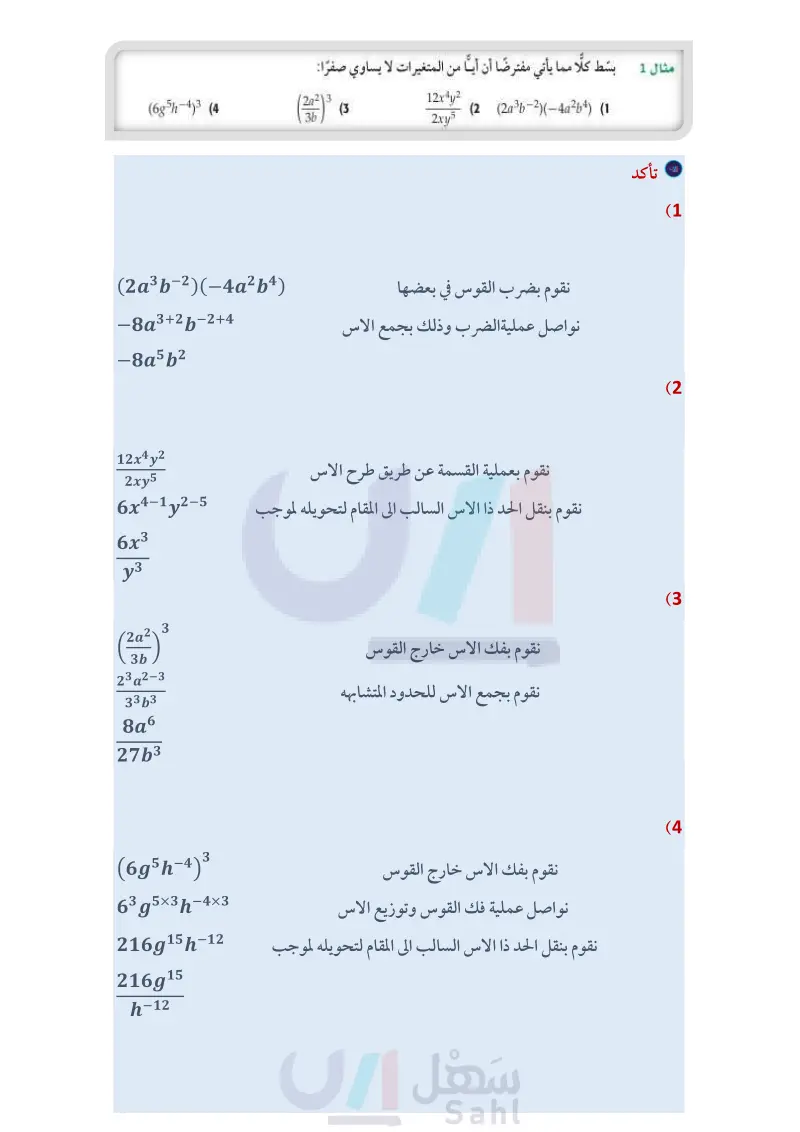
(6g5h-4)3 (4 تأكد مثال 1 بسط كلًا مما يأتي مفترضًا أن أيا من المتغيرات لا يساوي صفرا: 12x4y2 2xy5 (2 (2a3b-2)(-4a²b4) (1 2a2 3 (3 3b مثال 2 حدد ما إذا كانت كل عبارة فيما يأتي كثيرة حدود أم لا، وإن كانت كذلك فاذكر درجتها: 3x+4y (5 1x²-7y (6 الأمثلة 45 أوجد ناتج كل مما يأتي واكتبه في أبسط صورة: , , x² + √√√x (7 ab3 - 1 az4 + 3 (8 (3a4b) + (6a - 6b) (10 (n − 9)(n+7) (12 (x2 - 5x + 2) - (3x2 + x - 1) (9 - 3x2(2xy - 3xy2 + 4x2y3) (11 مثال 6 (13) رياضة يمارس عثمان رياضتي الركض السريع ورفع الأثقال مدة 75 دقيقة يوميًا. وعند ركضه يحرق 10 سعرات حرارية في الدقيقة، أما عندما يرفع الأثقال فيحرق 7.5 سعرات حرارية في الدقيقة. فإذا مارس رفع الأثقال x دقيقة في أحد الأيام، فاكتب كثيرة حدود تمثل عدد السعرات الحرارية التي حرقها في ممارسته للرياضتين ذلك اليوم. تمارين ومسائل مثال 1 بسط كلا مما يأتي مفترضًا أن أيا من المتغيرات لا يساوي صفرًا: (5x3y-5)(4xy³) (14 -1325 y223 (15 -7x5y5z4 21x7y5z2 (16 (15)4 (17 مثال 2 حدد ما إذا كانت كل عبارة فيما يأتي كثيرة حدود أم لا، وإن كانت كذلك فاذكر درجتها: 2x2 - 3x + 5 (18 a3-11 (19 الأمثلة 3,45 أوجد ناتج كل مما يأتي، واكتبه في أبسط صورة: √m -7 (21 5np n² 2g h (20 4x(2x2 + y) (23 (a+b)(a³-3ab – b²) (25 (6a2 + 5 + 10) - (4a2 + 6a + (12) (22 - (x − y)(x² + 2xy + y²) (24 مثال 6 (26 مزرعة : استأجر سلمان عاملين بالتناوب لتنسيق مزرعته، فإذا تقاضى الأول 200 ريال عن كل يوم عمل، وتقاضى الثاني 150 ريالًا عن كل يوم عمل، واحتاجت المزرعة إلى 15 يوم عمل لتنسيقها، فاكتب كثيرة حدود تمثل تكلفة تنسيق المزرعة إذا عمل الأول مدة x يومًا. بسط كلا مما يأتي مفترضًا أن أيا من المتغيرات لا يساوي صفرا: (a2b3)(ab)-2 (29 4x-243 xy-4 -2 (28 8x2y3 (27 24x3y2 18² (8g + 12h — 16gh²) (32 - 3c2d(2c3d5) 15c4d2 a-3b2(ba3 + b-1a2 + b2a) (34 (31 (-3x³y)2(4xy²) (30 x-2(x² - 3x3 + x-1) (33 (2x-2y)³ (36 ― (n² 7)(2n³ + 4) (35 وزارة التعليم Ministry of Education الدرس 3- العمليات على كثيرات الحدود 212914

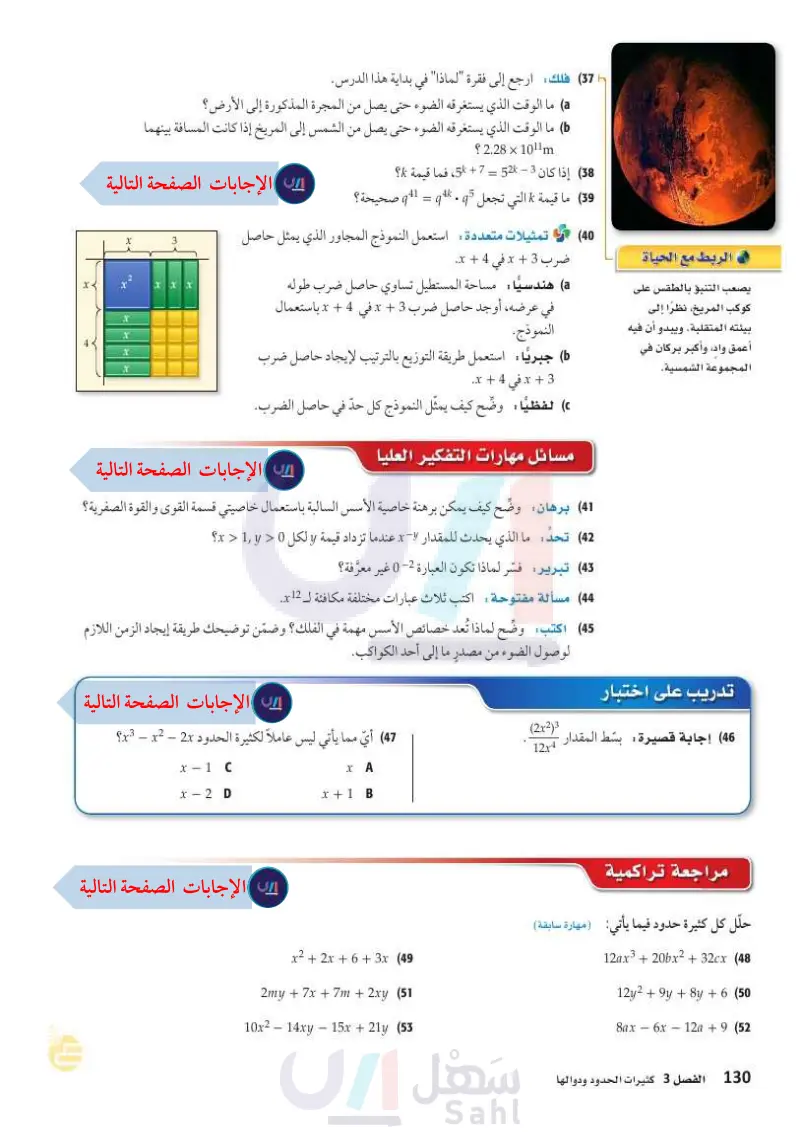
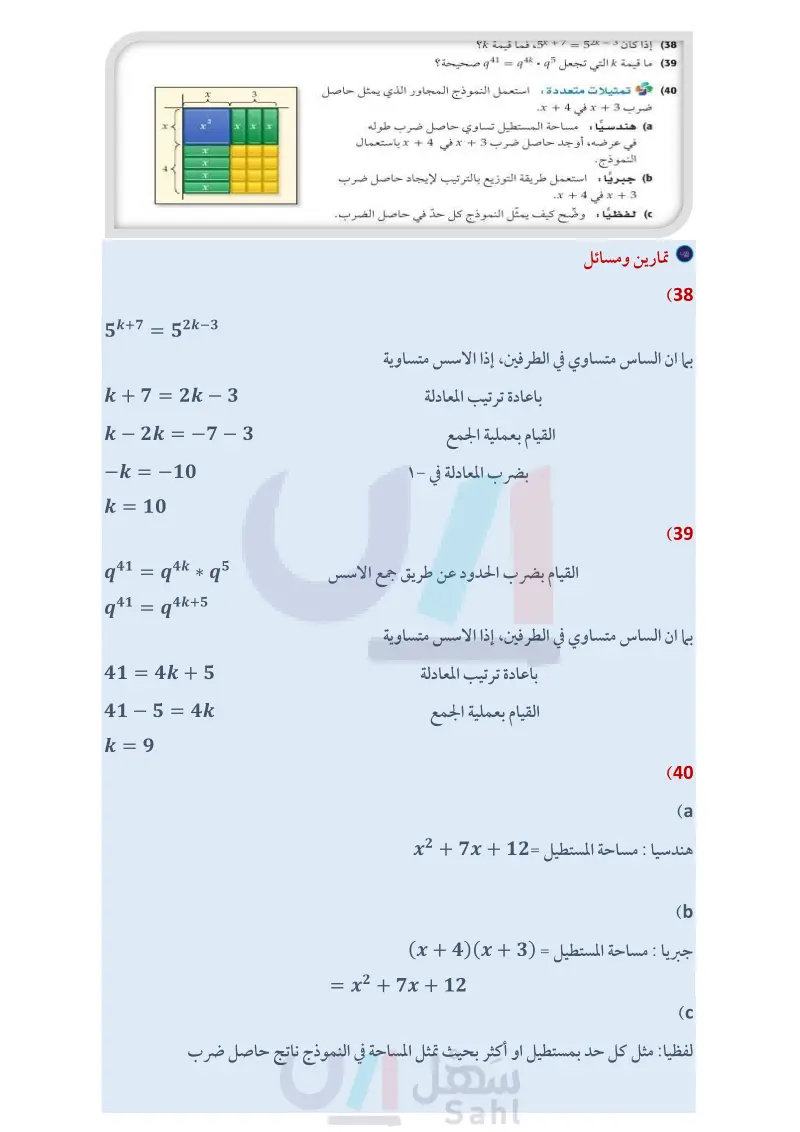
الربط مع الحياة يصعب التنبؤ بالطقس على كوكب المريخ، نظرا إلى بيئته المتقلبة. ويبدو أن فيه أعمق واد، وأكبر بركان في المجموعة الشمسية. (37) فلك : ارجع إلى فقرة "لماذا" في بداية هذا الدرس ما الوقت الذي يستغرقه الضوء حتى يصل من المجرة المذكورة إلى الأرض؟ ما الوقت الذي يستغرقه الضوء حتى يصل من الشمس إلى المريخ إذا كانت المسافة بينهما 1011m × 2.28 ؟ 38) إذا كان 3 - 52 = 7 + 5، فما قيمة ؟ (39) ما قيمة التي تجعل 15 . 4k = 941 صحيحة ؟ k (40) تمثيلات متعددة: استعمل النموذج المجاور الذي يمثل حاصل ضرب 3 + x في 4 + x. هندسيا مساحة المستطيل تساوي حاصل ضرب طوله في عرضه، أوجد حاصل ضرب 3 + x في 4 + x باستعمال النموذج. جبريًا: استعمل طريقة التوزيع بالترتيب لإيجاد حاصل ضرب 3 + x في 4 + x. لفظيا وضّح كيف يمثل النموذج كل حدّ في حاصل الضرب. : مسائل مهارات التفكير العليا X 3 2 x x XXX X X 4 x X 41 برهان وضّح كيف يمكن برهنة خاصية الأسس السالبة باستعمال خاصيتي قسمة القوى والقوة الصفرية؟ (42) تحد ما الذي يحدث للمقدار x عندما تزداد قيمة y لكل 0 < x > 1, y؟ : (43) تبرير فسّر لماذا تكون العبارة 2-0 غير معرفة؟ (44) مسألة مفتوحة : اكتب ثلاث عبارات مختلفة مكافئة لـ x12 . (45) اكتب وضّح لماذا تُعد خصائص الأسس مهمة في الفلك؟ وضمن توضيحك طريقة إيجاد الزمن اللازم لوصول الضوء من مصدر ما إلى أحد الكواكب. (47) أي مما يأتي ليس عاملاً لكثيرة الحدود x3 - x2 – 2x وزارة التعليم Ministry of Education 2024-1446 x - 1 C x-2 D X A x + 1 B x2 + 2x + 6 + 3x (49 2my + 7x + 7m + 2xy (51 10x2 – 14xy – 15x + 21y (53 (2x2)3 12x4 تدريب على اختبار (46) إجابة قصيرة : بسّط المقدار . مراجعة تراكمية حلل كل كثيرة حدود فيما يأتي: (مهارة سابقة) 12ax3 + 20bx2 + 32cx (48 12y2 + 9y + 8y + 6 (50 8ax 6x 12a + 9 (52 الفصل 3 كثيرات الحدود ودوالها 130