حل المعادلات التربيعية بيانيا - الرياضيات 3 - ثالث متوسط
الفصل8: الدوال التربيعية
الفصل9: المعادلات الجذرية والمثلثات
الفصل 10: الإحصاء والاحتمال
نشاط الفصل8: الدوال التربيعية
نشاط الفصل9: المعادلات الجذرية والمثلثات
نشاط الفصل10: الإحصاء والاحتمال
Y-A حل المعادلات التربيعية بيانيا رابط الدرس الرقمي فيما سبق درست حل المعادلات الماذا ؟ يعبر عن المسار المنحني لكرة قدم ركلت داخل ملعب بالدالة ص = - س ٢ + ۱۸ س؛ حيث (س) المسافة الأفقية التي قطعتها الكرة بالأمتار ، (ص) ارتفاع الكرة فوق سطح الأرض التربيعية بالتحليل إلى العوامل. والآن بالأمتار. ويمكن استعمال المقاطع السينية للتمثيل البياني لهذه الدالة لتحديد المسافة الأفقية التي ستقطعها الكرة حتى تلمس . أحل المعادلات التربيعية الأرض. بيانيا. www.ien.edu.sa . أقدر حلول المعادلات حل المعادلة التربيعية بالتمثيل البياني: الصورة القياسية للمعادلة التربيعية هي: التربيعية من تمثيلها أس + ب س + جـ = . ، حيث أ . ، ولكتابة الدالة التربيعية على صورة معادلة، استبدل ص أو د (س) بصفر، وتذكّر أن حلول المعادلة أو جذورها يمكن تحديدها بإيجاد المقاطع السينية للتمثيل البياني للدالة المرتبطة، ويوجد للمعادلة التربيعية حلان حقيقيان أو حل حقيقي واحد، أو لا يوجد لها حلول حقيقية. البياني. المفردات الجذر المكرر مفهوم أساسي حلول المعادلات التربيعية أضف إلى طوبتك ۲۲ w حلان حقيقيان مختلفان حل حقيقي وحيد لا يوجد حلول حقيقية مثال ۱ جذران حقيقيان مختلفان حل المعادلة س ۲ - ۲ س - ۸ = - بيانيا. مثل الدالة د (س) = س ۲ - ۲ س - ٨ المرتبطة بالمعادلة بيانيا. تظهر المقاطع السينية للتمثيل البياني عند - ۲ ، ٤ ؛ لذا فالحلول هي - ٢، ٤ تحقق، تحقق من صحة كل حل بالتعويض في المعادلة الأصلية. س ۲ - ۲ س - ۸ = ۰ المعادلة الأصلية (-A) A(-A) V** س = ٢ أو س = ٤ ✓... سط. تحقق من فهمك س ۲ - ۲ س - ۸ = ۰ ٤( ٢ - ٢)٤( - ٠٤٨) ✓ ... (أ) - س ۲ - ۳ س + ۱۸ = ۰ اب) س ٢ - ٤ س + ٣ - ٠ حلول المعادلة في مثال ۱ عددان حقيقيان مختلفان، إلا أنه أحيانا يكون الجذران هما العدد نفسه، ويُسمّى عندها جذرًا مكرّرًا. الفصل :: الدوال التربيعية وزارة التعليم Ministry of Education 2024-1446

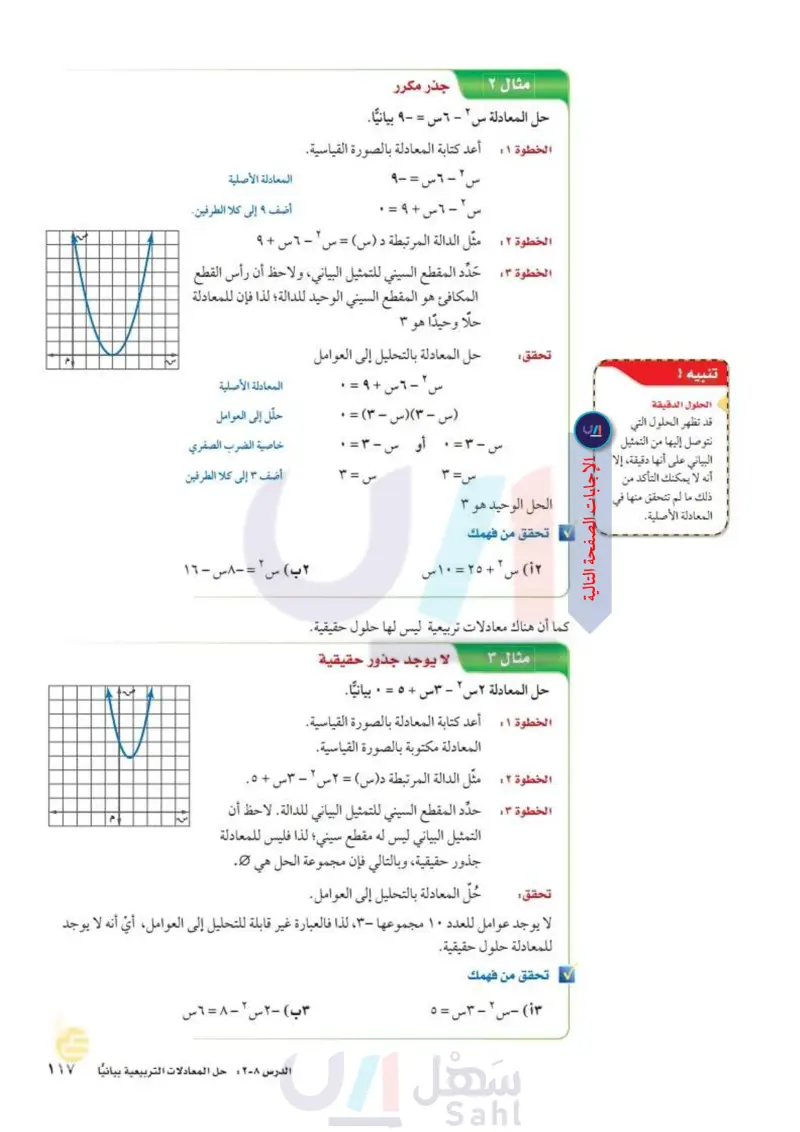
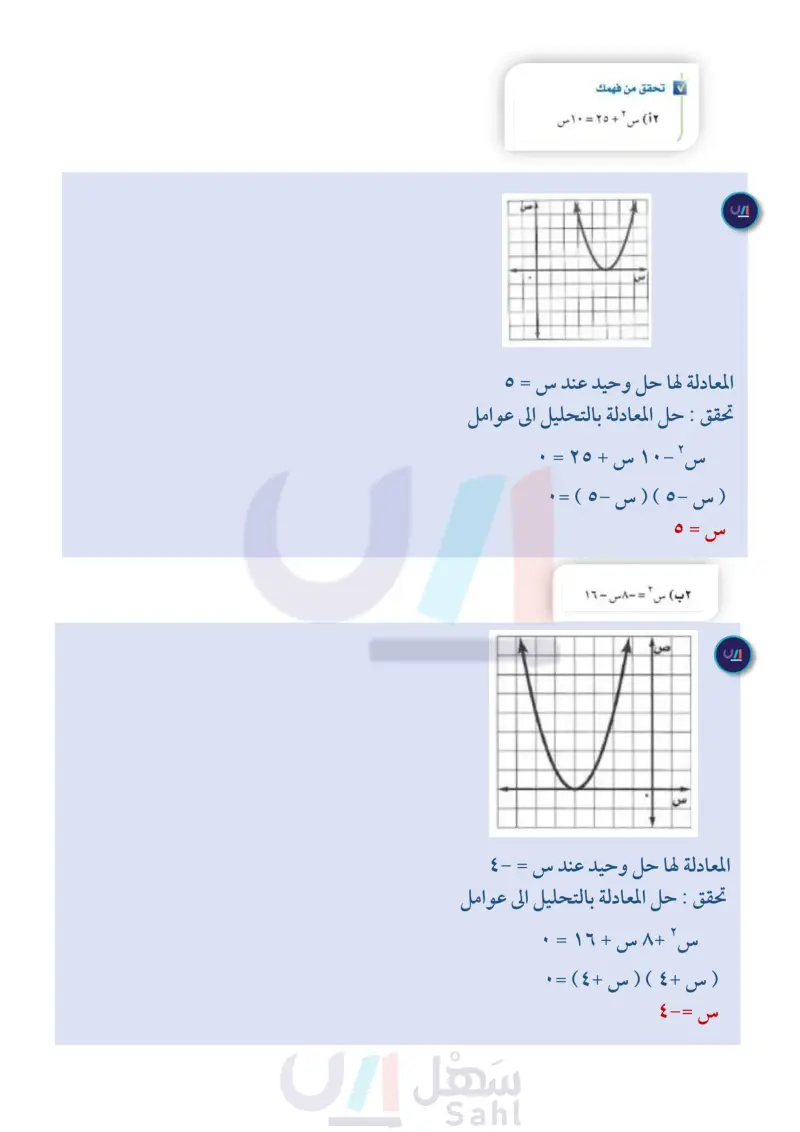
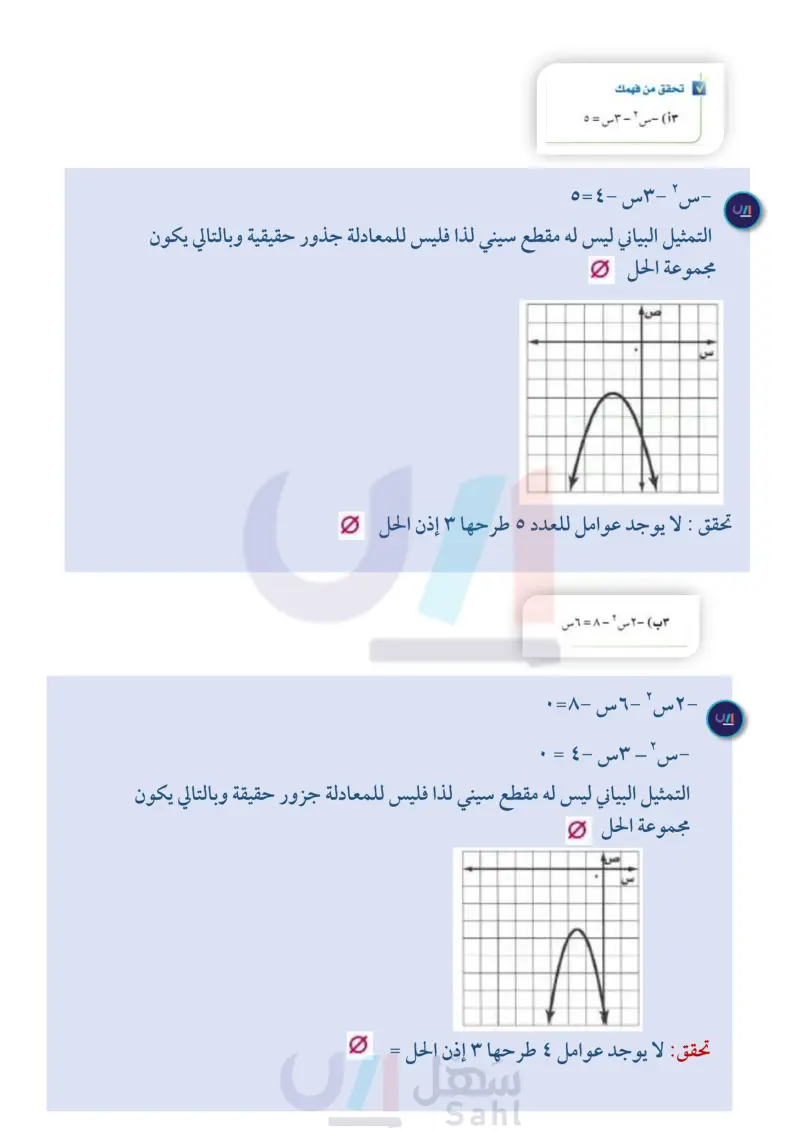
تنبيه : الحلول الدقيقة قد تظهر الحلول التي نتوصل إليها من التمثيل البياني على أنها دقيقة، إلا أنه لا يمكنك التأكد من ذلك ما لم تتحقق منها في المعادلة الأصلية. مثال ۲ جذر مكرر حل المعادلة س ٢ - ٦ س = - ٩ بيانيا. الخطوة ١: أعد كتابة المعادلة بالصورة القياسية. س ٢ - ٦ س = - ٩ س ٢ - ٦ س + ٩ = ٠ المعادلة الأصلية أضف 9 إلى كلا الطرفين. الخطوة ٢ . مثل الدالة المرتبطة د (س) = س ٢ - ٦ س + ٩ الخطوة : حدد المقطع السيني للتمثيل البياني، ولاحظ أن رأس القطع المكافئ هو المقطع السيني الوحيد للدالة؛ لذا فإن للمعادلة حلا وحيدا هو ؟ تحقق حل المعادلة بالتحليل إلى العوامل س ٢ - ٦ س + ٩ - ٠ المعادلة الأصلية س - ۳) (س - ۳) = ۰ حلل إلى العوامل س - = . أو س – ۳ = . خاصية الضرب الصفري س = 3 أضف ٣ إلى كلا الطرفين س = ٣ الحل الوحيد هو ٣ تحقق من فهمك (۱) س + ۲۵ - ۱۰ س كما أن هناك معادلات تربيعية ليس لها حلول حقيقية. مثال ۳ لا يوجد جذور حقيقية حل المعادلة ٢ س ٢ - ٣س + ٥ = • بيانيا. الخطوة 1: أعد كتابة المعادلة بالصورة القياسية. المعادلة مكتوبة بالصورة القياسية. ٢ ب س ٢ = -٨س - ١٦ الخطوة ٢ : مثل الدالة المرتبطة د(س) = ٢ س٢ - ٣س + ٥ . الخطوة : حدد المقطع السيني للتمثيل البياني للدالة. لاحظ أن التمثيل البياني ليس له مقطع سيني؛ لذا فليس للمعادلة تحقق جذور حقيقية، وبالتالي فإن مجموعة الحل هي . حل المعادلة بالتحليل إلى العوامل. لا يوجد عوامل للعدد ۱۰ مجموعها - ٣، لذا فالعبارة غير قابلة للتحليل إلى العوامل، أي أنه لا يوجد للمعادلة حلول حقيقية. تحقق من فهمك ۱۳) - س ٢ - ٣س = ٥ الدرس ۸-۲ حل المعادلات التربيعية بيانيا الـ التصميم Ministry of Eduration 2024-1446

قد تظهر الحلول الت تتوصل إليها التمثل البياني على أنها دقيقة
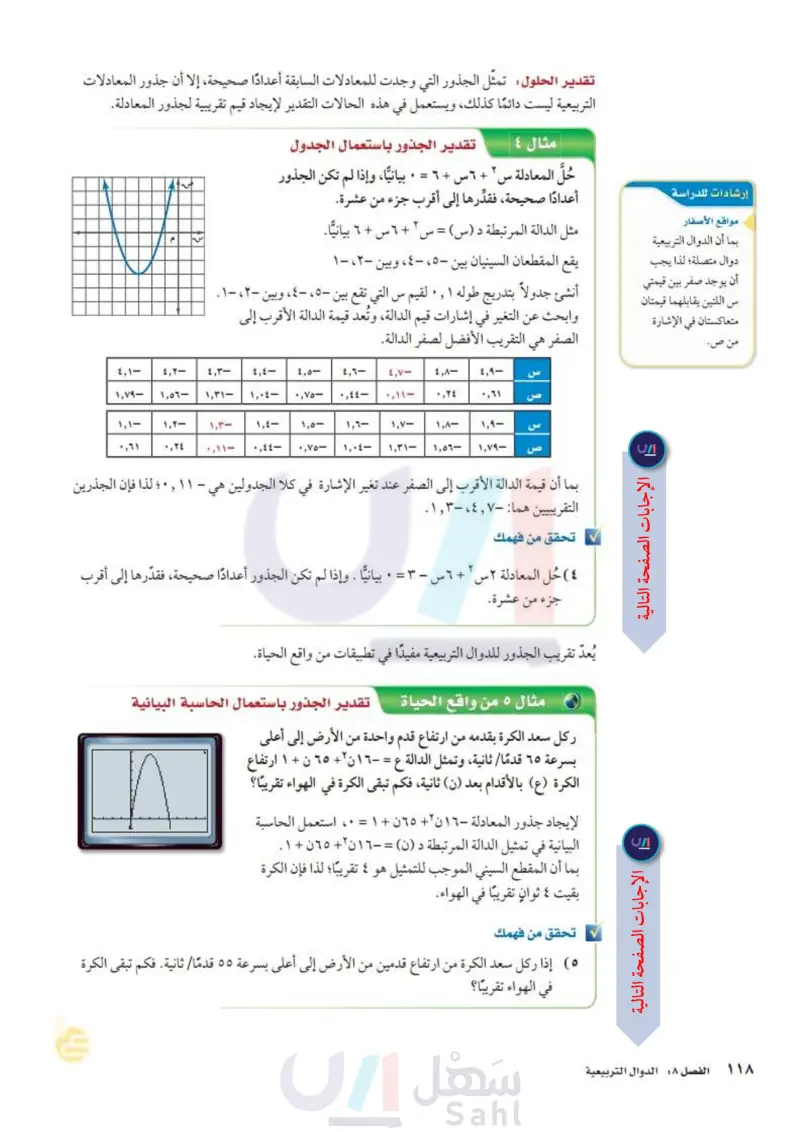
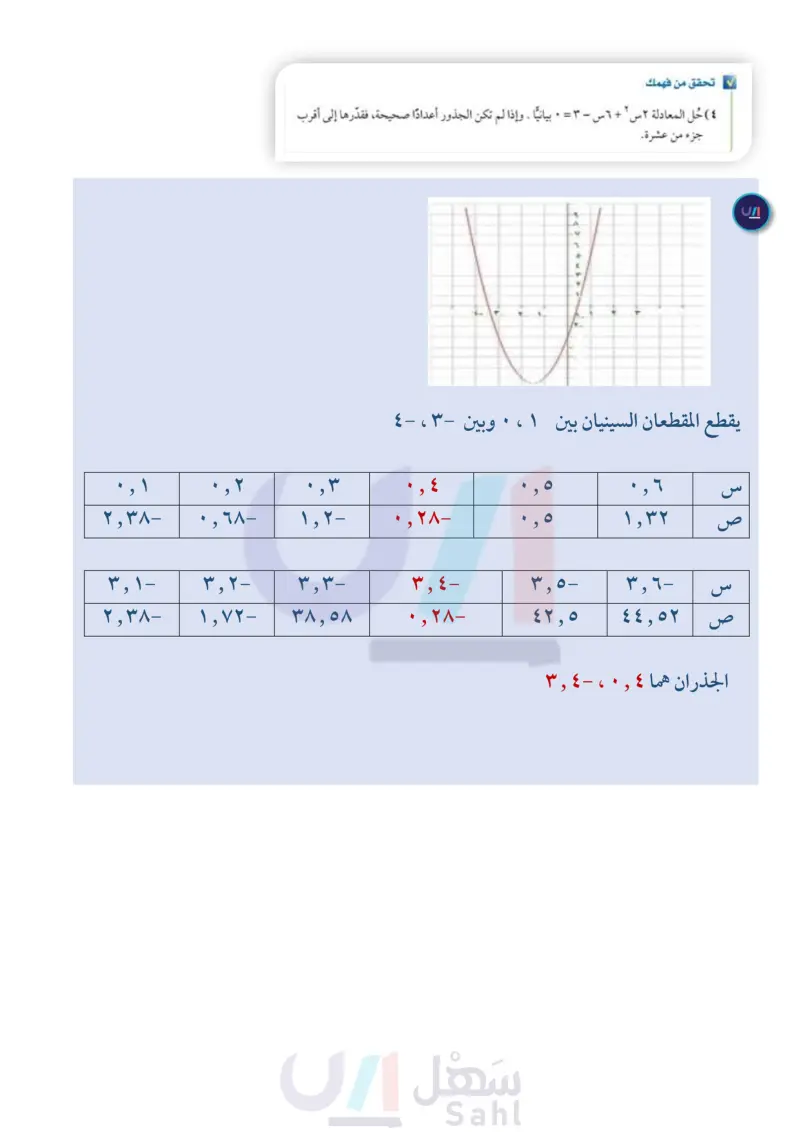
إرشادات للدراسة مواقع الأصفار بما أن الدوال التربيعية دوال متصلة؛ لذا يجب تقدير الحلول تمثل الجذور التي وجدت للمعادلات السابقة أعدادًا صحيحة، إلا أن جذور المعادلات التربيعية ليست دائما كذلك، ويستعمل في هذه الحالات التقدير لإيجاد قيم تقريبية لجذور المعادلة. مثال ٤ تقدير الجذور باستعمال الجدول حُلَّ المعادلة س ٢ + ٦ س + ٦ = • بيانيا، وإذا لم تكن الجذور أعدادًا صحيحة، فقدرها إلى أقرب جزء من عشرة. مثل الدالة المرتبطة د (س) = س ٢ + ٦ س + ٦ بيانيا. يقع المقطعان السينيان بين ٥، ٤ ، وبين -٢، ١ أن يوجد صفر بين قيمتي أنشئ جدولاً بتدريج طوله ٠٫١ لقيم س التي تقع بين -٥، ٤، وبين -٢، ١. س اللتين يقابلهما قيمتان متعاكستان في الإشارة من ص. وابحث عن التغير في إشارات قيم الدالة، وتعد قيمة الدالة الأقرب إلى الصفر هي التقريب الأفضل لصفر الدالة. ٢٤ الفصل : الدوال التربيعية س ص س ص 1,1- ٤,٢ ٤,٣ 1,19- 1,09- 1,1- ١,٠٤- ۱,۳۱- 10- 1,7- -vo- ٤,٧ -11- 11- 1,A- 19- ٠,٢٤ 31 1,1- ٠,٦١ ۱,۲ 1- 1.0- 1,1- ۱,۷ 1,A- 1,9- ٠,٢٤ -11- +311- ۰,۷۵ 1,19- 1,07- ۱,۳۱- ١,٠٤- بما أن قيمة الدالة الأقرب إلى الصفر عند تغير الإشارة في كلا الجدولين هي – ۰,۱۱؛ لذا فإن الجذرين التقريبيين هما: ٤٧ - ١٣ تحقق من فهمك ٤ ) حل المعادلة ٢ س ٢ + ٦ س - ٣ - ٠ بيانيًا . وإذا لم تكن الجذور أعدادًا صحيحة، فقدرها إلى أقرب جزء من عشرة. يعد تقريب الجذور للدوال التربيعية مفيدًا في تطبيقات من واقع الحياة. مثال ٥ من واقع الحياة تقدير الجذور باستعمال الحاسبة البيانية = ركل سعد الكرة بقدمه من ارتفاع قدم واحدة من الأرض إلى أعلى بسرعة ٦٥ قدما ثانية، وتمثل الدالة ع - - ١٦ ن ٢ + ٦٥ ن + ١ ارتفاع الكرة (ع) بالأقدام بعد (ن) ثانية، فكم تبقى الكرة في الهواء تقريبا؟ لإيجاد جذور المعادلة - ١٦ ن ٢ + ٦٥ن + ١ = ٠، استعمل الحاسبة البيانية في تمثيل الدالة المرتبطة د (ن) = - ١٦ن + ٦٥ن + ١ . بما أن المقطع السينى الموجب للتمثيل هو ٤ تقريبا؛ لذا فإن الكرة بقيت 4 ثواني تقريبا في الهواء. تحقق من فهمك (0) إذا ركل سعد الكرة من ارتفاع قدمين من الأرض إلى أعلى بسرعة ٥٥ قدما ثانية. فكم تبقى الكرة في الهواء تقريبا؟ وزارة التعليم Ministry of Education 2024-1446

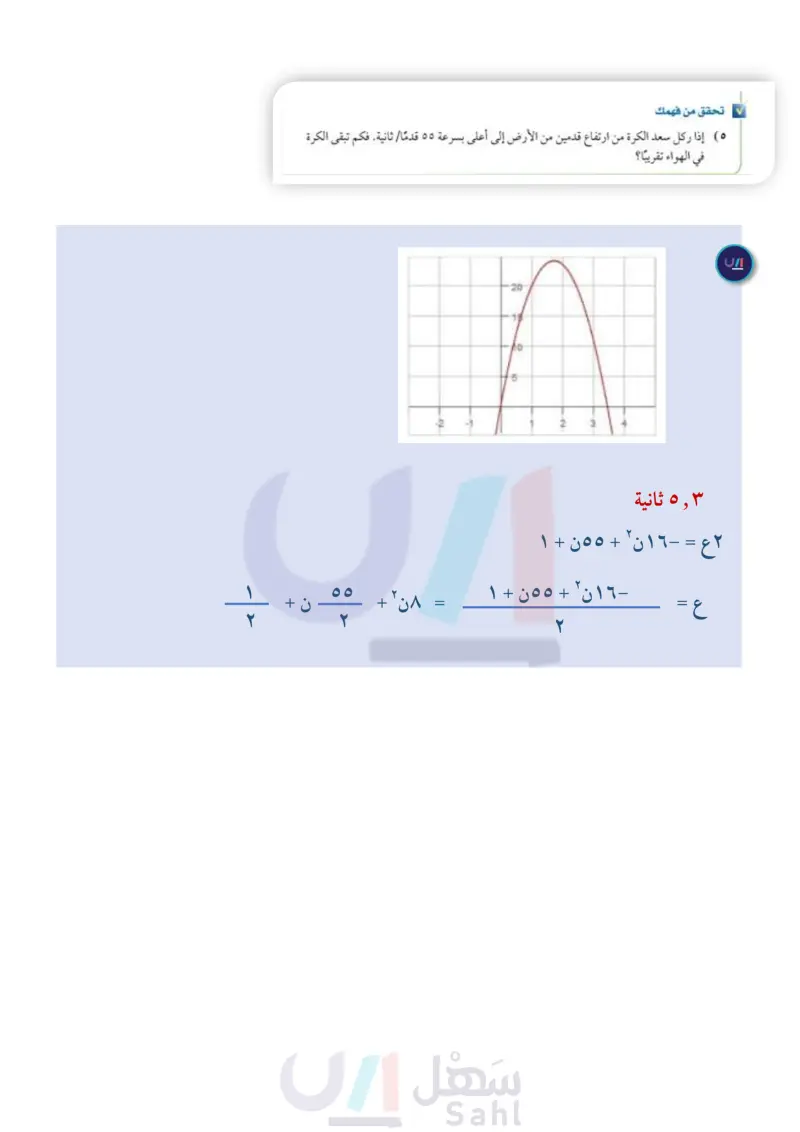
إذا ركل الكرة سعد من ارتفاع قدمين من الأرض إلى أعلى بسرعة 55 قدماً في الثانية فكم تبقى الكرة في الهواء تقريباً؟


بما أن الدوال التربيعية دوال متصلة لذا يجب أن يوجد صفرين
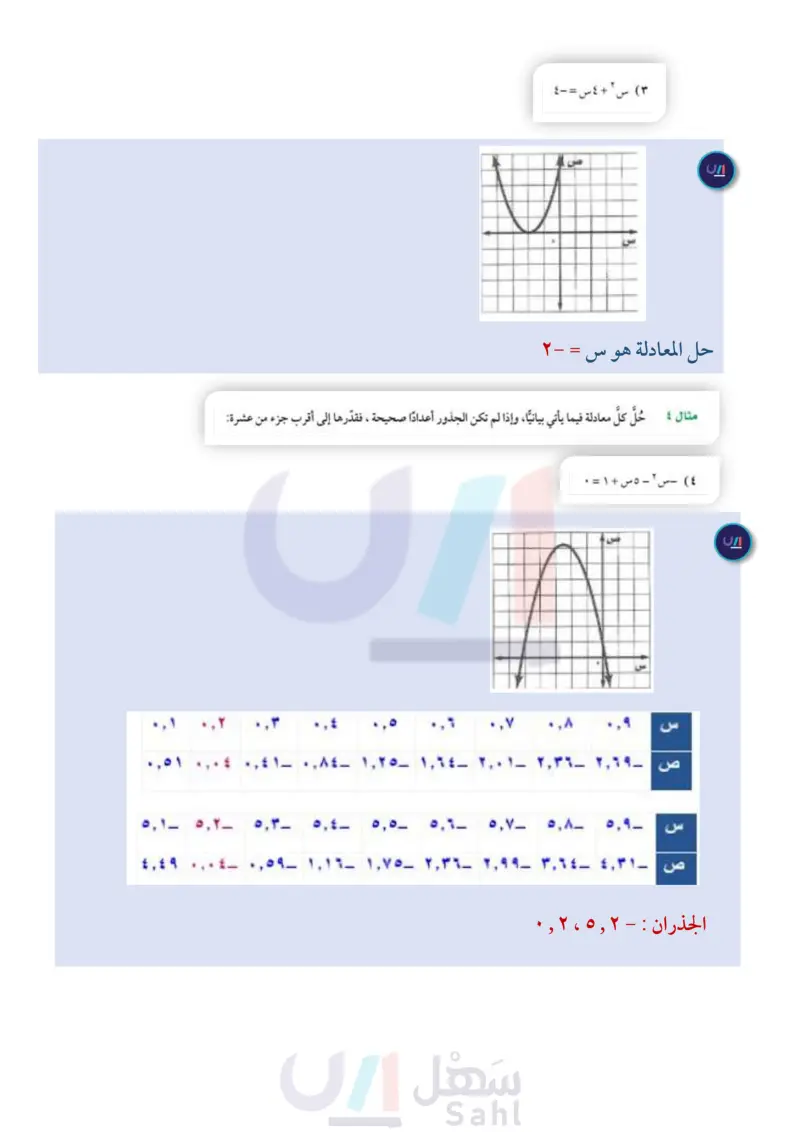
تأكد الأمثلة ١ - ٣ تقنية: حل كل معادلة فيما يلي بيانيًا باستخدام أحد التطبيقات الحاسوبية. 1) س ۲ - ۳ س - ۱۰ - ۰ ۲) ۲س ۲ - ۸س = ۰ ٣) س ٢ + ٤ س = -٤ مثال ٤ حُلَّ كلّ معادلة فيما يأتي بيانيًا، وإذا لم تكن الجذور أعدادًا صحيحة ، فقدرها إلى أقرب جزء من عشرة: (٤) س ۲ - ۵ س + ۱ = ۰ ٥) -۹ - س ٢ (٦) س ٢ = ٢٥ مثال ٥ معرض العلوم إذا صمّم نواف نموذجا لصاروخ يمكنه أن ينطلق في الهواء وفق سرعة الصاروخ المعادلة المبينة في الشكل، حيث (ع) ارتفاع الصاروخ بالأقدام بعد (ن) ثانية من انطلاقه، فكم يبقى الصاروخ في الهواء تقريبا؟ ١٣٥ قدما / ث ع - -١٦ ن' + ١٣٥ن تدرب وحل المسائل الأمثلة ١ - ٣ حُلَّ كل معادلة فيما يأتي بيانيا : س ٢ + ٧س + ١٤ = ٠ (۹) س ٢ + ۲ س - ٢٤ - ٠ ۱۰) س ۲ - ۲ س - ۱ مثال ٤ حلّ كل معادلة فيما يأتي بيانيًّا، وإذا لم تكن الجذور أعدادًا صحيحة، فقدرها إلى أقرب جزء من عشرة: (۱۱) س ۲ + ۲ س - ۹ - ۰ ۱۲) س ٢ - ٤ س = ٢٠ ۱۳) س ۲ - ۳س = ۱۸ مثال ٥ ١٤ أفعوانية ترتفع أفعوانية براكبيها إلى الأعلى، ثم تنزل بهم إلى الأسفل وفق المعادلة: ع - - ١٦ ن ۲ + ۱۸٥ن، حيث (ع) الارتفاع بالأقدام بعد (ن) ثانية، فكم ثانية تستغرق الأفعوانية للعودة إلى الأسفل ؟ استعمل التحليل إلى العوامل لتحديد عدد المرات التي يقطع فيها التمثيل البياني محور السينات في كل دالة مما يأتي، ثم حدد أصفار كل منها: ١٥ ص = س ٢ - ٨س + ١٦ (١٦) ص = س ٢ + ٣س + ٤ ۱۷ ص = س ۲ + ۱۲ س + ۳۲ ۱۸) نظرية الأعداد: استعمل معادلة تربيعية لإيجاد عددين مجموعهما ٩، وناتج ضربهما ۲۰. ۱۹) تمثيلات متعددة: ستكتشف في هذه المسألة كيفية تفسير العلاقة بين الدوال التربيعية وتمثيلاتها البيانية. أ بيانيا : مثل الدالة ص = س ٢ . ب تحليليا اكتب إحداثيات الرأس وإحداثيات نقطتين على التمثيل. جـ) بيانيا : مثل الدوال ص = س ۲ + ۲ ، ص = س ٢ + ٤ ، ص = س ٢ + ٦ بيانيا على المستوى الإحداثي السابق نفسه. د) تحليليا اكتب إحداثيات الرأس وإحداثيات نقطتين على كل من هذه التمثيلات التي لها الإحداثيات السينية نفسها. ماذا تستنتج ؟ الدرس ۸-۲ حل المعادلات التربيعية بيانيا Ministry o 2024-1446

تدرب وحل المسائل حل كل معادلة فيما يأتي بيانياً وإذا لم تكن الجذور أعداد صحيحة فقدرها إلى أقرب جزء من عشرة:

تدرب وحل المسائل حل كل معادلة فيما يأتي بيانياً وإذا لم تكن الجذور أعداداً صحيحية فقدرها إلى أقرب جزء من عشرة

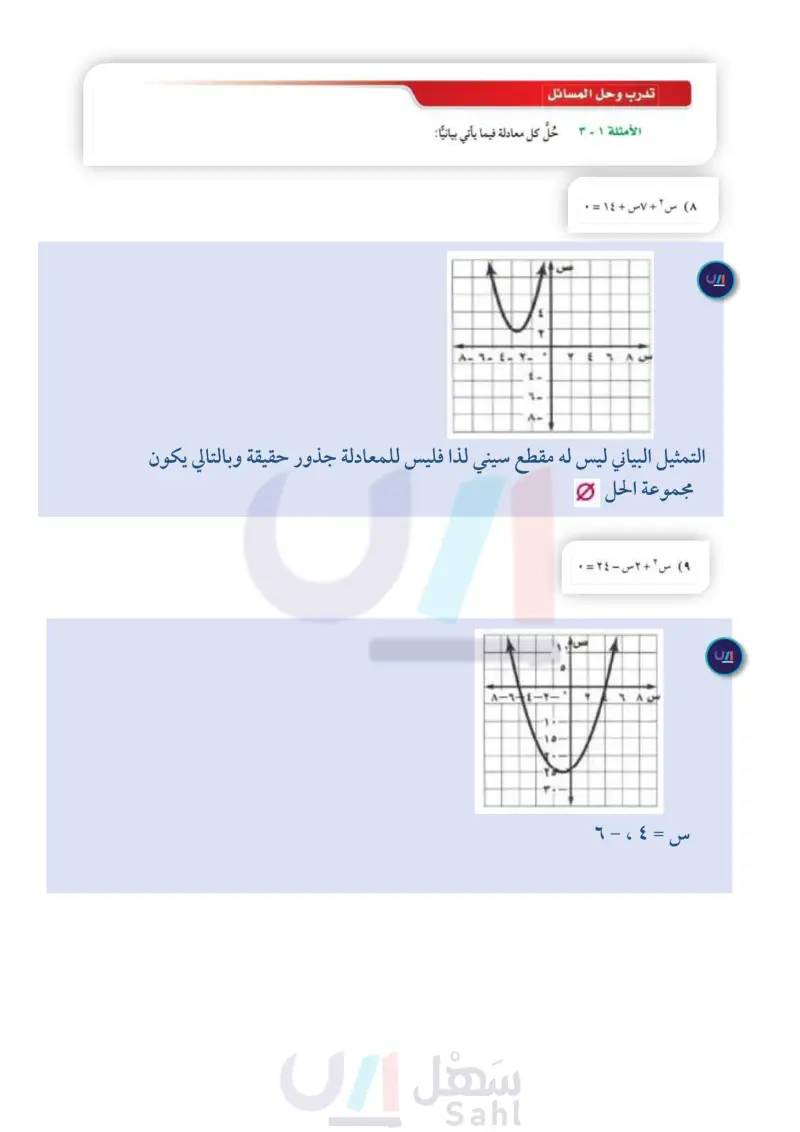
تدريب على اختبار مسائل مهارات التفكير العليا ٢٠ اكتشف الخطأ يقوم معاذ وأحمد بإيجاد عدد الأصفار الحقيقية للدالة الممثلة بالشكل المجاور، فيقول معاذ إنه ليس لهذه الدالة أصفار حقيقية؛ لأنه لا يوجد لتمثيلها البياني مقاطع سينية، بينما يقول أحمد: إن لها صفرا حقيقيا واحدًا؛ لأن للتمثيل البياني للدالة مقطعا صاديًا. فأيهما كانت إجابته صحيحة؟ فسّر إجابتك. ۲۱) مسألة مفتوحة : صف مسألة من واقع الحياة يتم فيها قذف جسم في الهواء، واكتب معادلة تمثل ارتفاع الجسم بالنسبة للزمن، وحدّد الفترة الزمنية التي يمكثها الجسم في الهواء. (۲۲) تحد اكتب معادلة تربيعية لها الجذور المذكورة في كل مما يأتي: (أ) جذر مكرر مرة واحدة. ب) جذر نسبي ( غير صحيح) واحد، وجذر صحيح واحد. ج) جذران صحيحان مختلفان و متعاكسان جمعيا. (۲۳) اكتب وضح كيف تقرّب جذور المعادلة التربيعية عندما لا تكون أعدادًا صحيحة. ٢٤ إذا حصل إبراهيم على الدرجة ٥٠ في اختبار درجته ٢٥) تمثل الصيغة ف = - جـن المسافة (ف) بالأمتار التي العظمى ٨٠. فما النسبة المئوية لدرجته في الاختبار؟ ب) ٦,٢٥ 71,1 (> %*, 17(a يقطعها جسم يسقط على كوكب سقوطا حرا بعد (ن) ثانية. اكتب الصيغة بدلالة المتغير جدء الذي يمثل تسارع ، الجاذبية. ججن ج) جن جن مراجعة تراكمية ب) ج = ۲ فن۲ SAY --+ (a أوجد إحداثيات الرأس، ومعادلة محور التماثل، وبين إذا كان الرأس يمثل قيمة عظمى أم قيمة صغرى، ثم مثل الدالة بيانيا : ( الدرس ۱۸) (۲۷) ص = س ٢ - ٦ س - ٨ (۲۸) ص = - ٤ س ٢ - ٨س + ٥ (۲۹) ص = ۳س + ۲ س + ۱ (٢٦) ص = ٣ س ٢ حُلَّ كل معادلة فيما يأتي، وتحقق من صحة الحل: (مهارة سابقة) ۲۳۰ س ٢ = ۳۲ ٣١) (س - ٢٤ = ٢٥ (٣٢ ٤ س ٢ - ٤ س + ١ = ١٦ ٣٣ ٢ س ٢ - ١٦ س = - ٣٢ استعد للدرس اللاحق ٣٥) ٩س ٢ + ٦س + ١ (٣٨ ٣٦ س ٢ - ٨٤س + ٤٩ مهارة سابقة: حدد ما إذا كانت كل ثلاثية حدود فيما يأتي تشكل مربعا كاملا، اكتب "نعم" أو "لا"، وإذا كانت كذلك فحللها : ٣٤ ١٦ س ٢ - ٢٤ س + ٩ ۳۷) س ۲ - ۸س + ۸۱ (٣٦) ٢٥ س ٢ - ٦٠ س + ٣٦ ٣٩ ٤ س ٢ - ٣س + ٩ ٢٦ الفصل : الدوال التربيعية وزارة التعليم Ministry of Education 2024-1446

أوجد إحداثيات الرأس ومعادلة محور التماثل وبين إذا كان الرأس يمثل قيمة عظمى أم قيمة صغرى ثم مثل الدالة بيانياً ص=3س

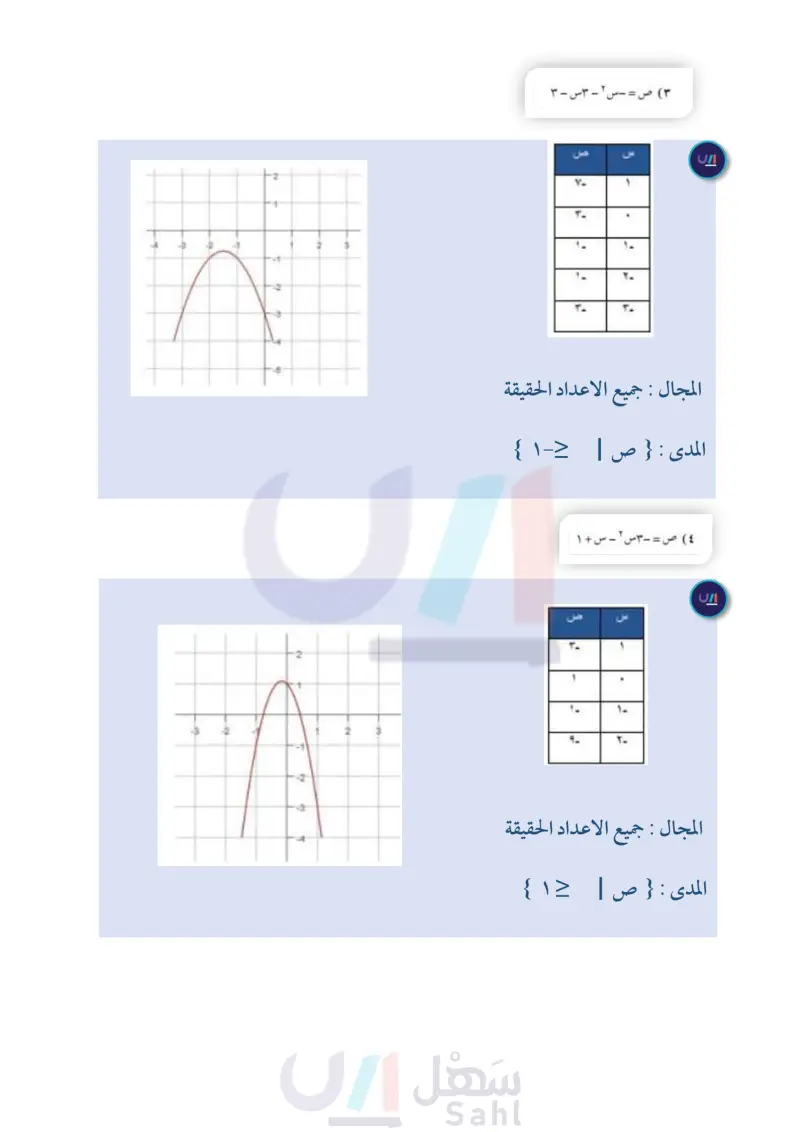
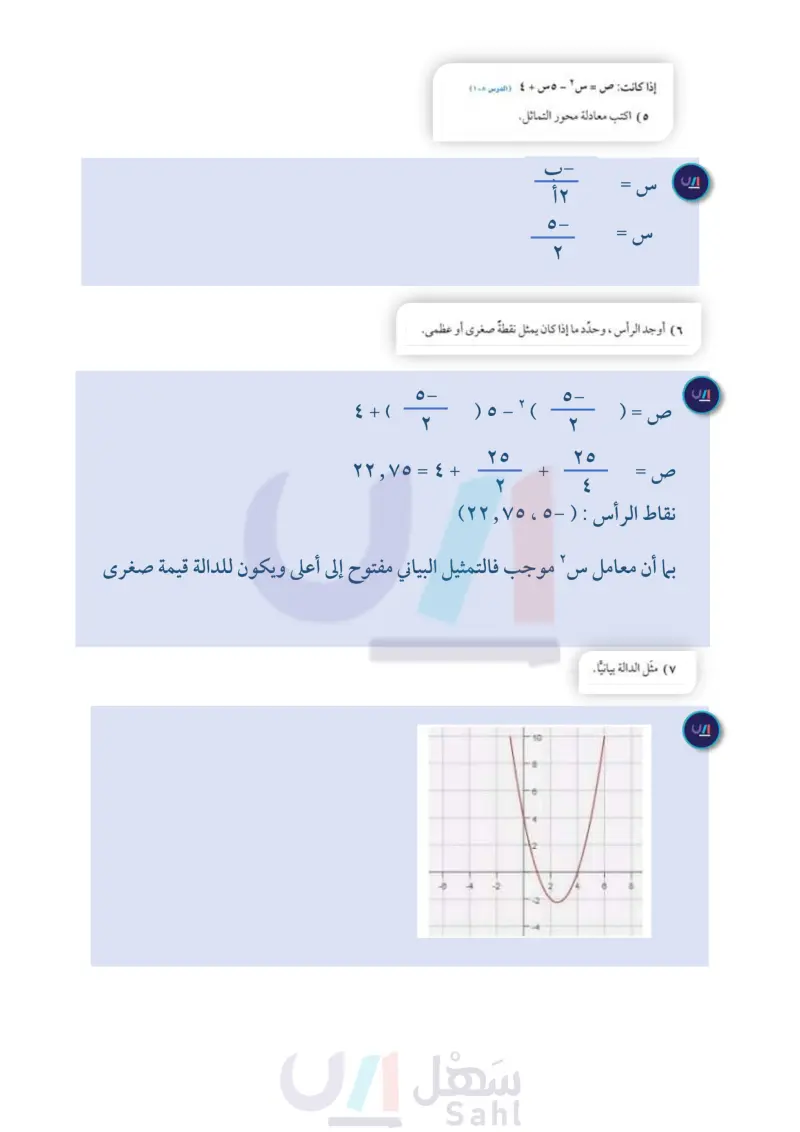
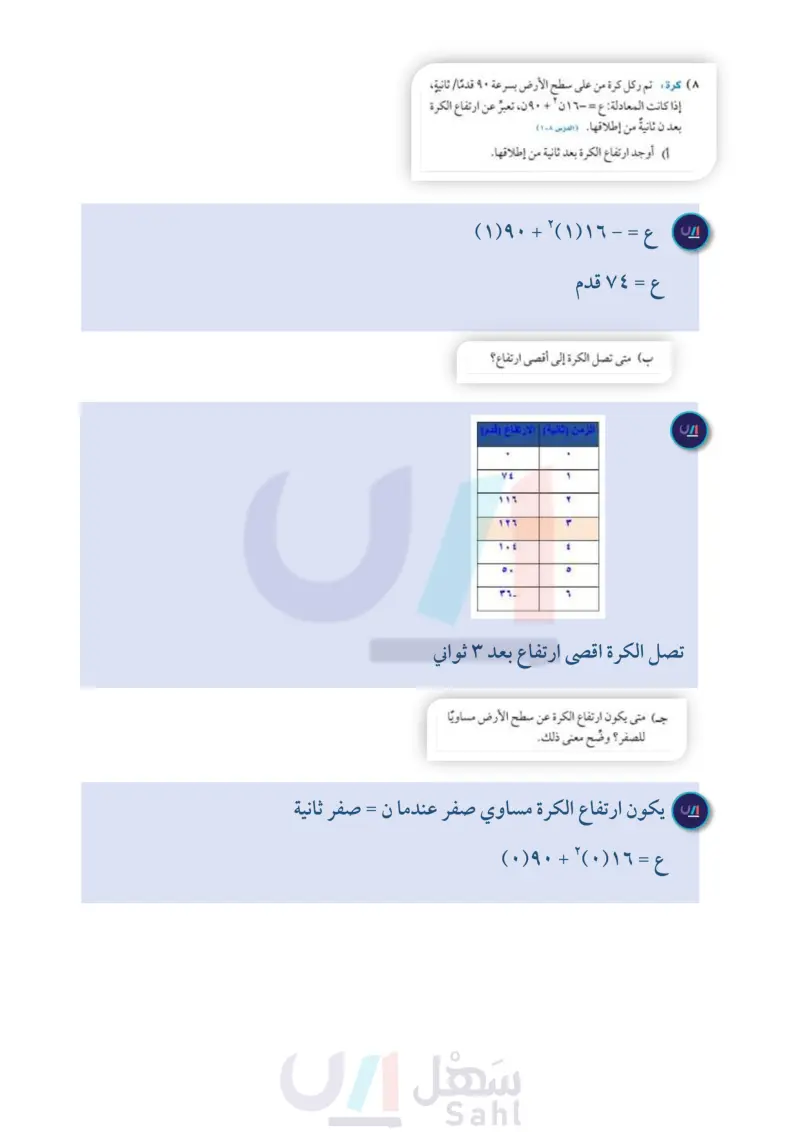
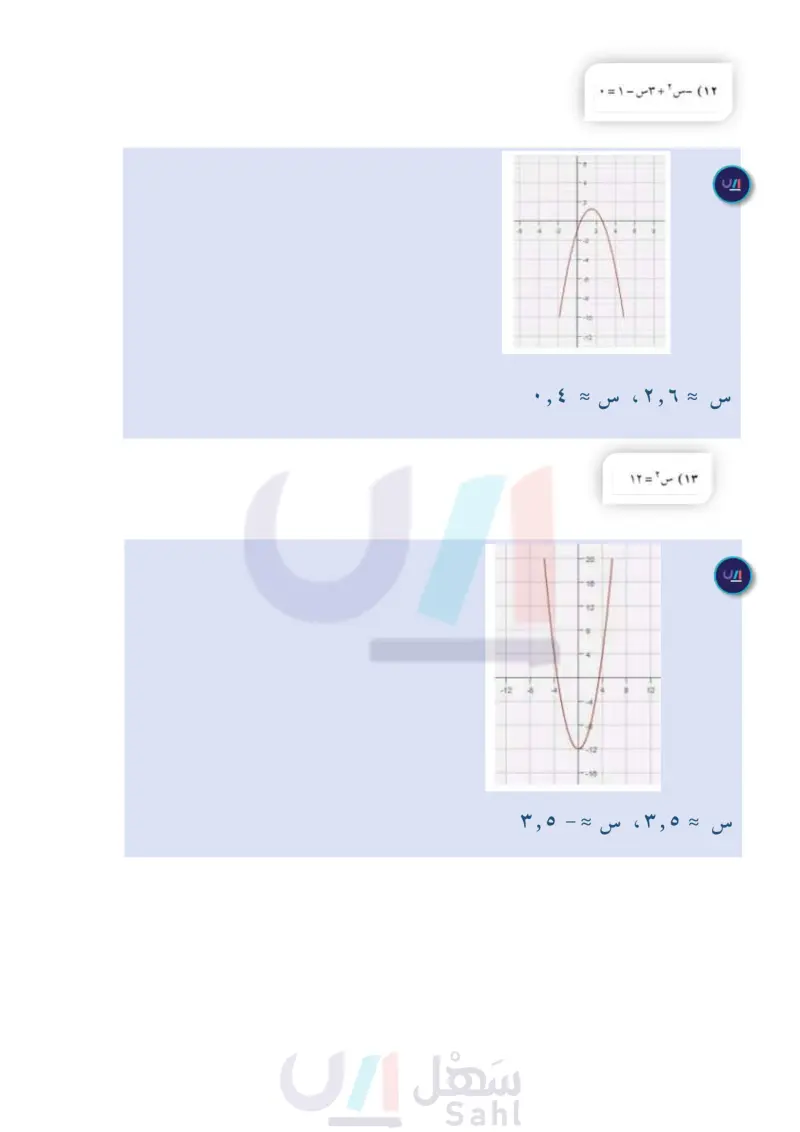
الفصل ٨ اختبار منتصف الفصل الدرسان ۸-۱ و ۸-۲ استعمل جدول القيم لتمثيل كل دالة فيما يأتي بيانيا، وحدد مجالها ۹) اختيار من متعدد التمثيل البياني للدالة: ومداها ( الدرس (۱۰۸) ۱) ص = س ۲ + ٣س + ۱ (۲) ص = ٢ س ٢ - ٤ س + ٣ ص = - س ۲ - ۳س - ۳ ٤ ص = - ۳س ۲ - س + ۱ إذا كانت: ص = س ٢ - ٥س + ٤ ( الدرس (۱۰۸) ه اكتب معادلة محور التماثل. ص = ۲ س ۲ - ۳س + ۱ ( الدرس (۱۰۸) أ) مفتوح إلى أعلى وله قيمة عُظمى. ب مفتوح إلى أعلى وله قيمة صُغُرَى. جـ) مفتوح إلى أسفل وله قيمة عُظمى. د) مفتوح إلى أسفل وله قيمة صُغُرَى. حل كل معادلة فيما يأتي بيانيًا، وإذا لم تكن الجذور أعدادًا صحيحةً فقدرها إلى أقرب جزء من عشرة (الدرس ۸-۲) (٦) أوجد الرأس ، وحدد ما إذا كان يمثل نقطة صغرى أو عظمى. (۱۰) س ٢ + ٥ س + ٦ = ٠ مثل الدالة بيانيا. (۱۱) س ٢ +٨ = - ٦س ۱۲) س ۲ - ۳ س - ۱ - ۰ ۱۳) س ۲ = ۱۲ كرة تم ركل كرة من على سطح الأرض بسرعة ٩٠ قدما ثانية، إذا كانت المعادلة : ع = - ١٦ ن ٢ + ۹۰ن، تعبر عن ارتفاع الكرة بعد ن ثانية من إطلاقها. (الدرس ۱۰۸) أ) أوجد ارتفاع الكرة بعد ثانية من إطلاقها. ب متى تصل الكرة إلى أقصى ارتفاع ؟ جـ) متى يكون ارتفاع الكرة عن سطح الأرض مساويًا للصفر؟ وضّح معنى ذلك. (١٤) كرة البيسبول : المعادلة : ع = - ١٦ ن ٢ + ١٢٠ن، تمثل ارتفاع كرة البيسبول بعد ن ثانيةً من ضربها، أوجد الوقت الذي تبقى فيه الكرة في الهواء. (الدرس ۸-۲) استعمل التحليل إلى عوامل؛ لتحديد عدد المرات التي يقطع فيها التمثيل البياني محور السينات في كل دالةٍ ممَّا يأتي، ثم حدد أصفار كل منها: (الدرس ۸-۲) ١٥ ص = س ۲ - ۳س + ۲ (١٦) ص = س ٢ ۱۷ ص = س ٢ + ٤ س + ٤ (۱۸) ص = س ۲ + س + ۳ الفصل : اختبار منتصف الفصل الت ٢٧ 2024-1446




 0
0