حل المعادلات والمتباينات الجذرية - رياضيات2-2 - ثاني ثانوي
الفصل الرابع: العلاقات والدوال العكسية والجذرية
الفصل الخامس: العلاقات والدوال النسبية
الفصل السادس: المتتابعات والمتسلسلات
نشاط الفصل الرابع: العلاقات والدوال العكسية والجذرية
نشاط الفصل الخامس: العلاقات والدوال النسبية
4-7 حل المعادلات والمتباينات الجذرية رابط الدرس الرقمي www.icn.edu.sa Solving Radical Equations and Inequalities الماذا؟ فيما سبق عندما تقفز إلى الأعلى فإنك ترتفع عن الأرض وتبقى زمنا معينًا في الهواء درست حل معادلات كثيرات الحدود. (مهارة سابقة ) يُسمى زمن التحليق. ويمكنك إيجاد زمن التحليق } بالثواني إذا علمت ارتفاع القفزة بالأقدام، وذلك باستعمال الصيغة 0.5 = t والان أحل معادلات تحتوي جذورا. أحل متباينات تحتوي جذورا المفردات المعادلة الجذرية إذا علم أن زمن تحليق أحد لاعبي كرة السلة 0.98 ثانية تقريبا، فكيف يمكنك حساب ارتفاع قفزته؟ حل المعادلات الجذرية تحتوي المعادلات الجذرية على عبارات جذرية يكون المتغير فيها تحت الجذر. ويمكنك حلها عن طريق رفع طرفي المعادلة لأس معين. radical equation الحل الدخيل extraneous solution المتباينة الجذرية radical inequality مفهوم أساسي حل المعادلات الجذرية الخطوة 1: اجعل الجذر في طرف واحد من المعادلة الخطوة 2 : ارفع طرفي المعادلة لقوة مساوية لدليل الجذر؛ وذلك للتخلص من الجذر الخطوة 3 : حل معادلة كثيرة الحدود الناتجة، ثم تحقق من صحة الحل. أضف إلى مطويتك عند حل بعض المعادلات الجذرية، قد لا يحقق الحل المعادلة الأصلية. ويُسمى مثل هذا الحل حلا دخيلًا. مثال 1 حل معادلات جذرية حلّ كل معادلة مما يأتي: Vx + 2 + 4 = 7 Vx + 2 + 4 = 7 Vx + 2 = 3 (√x + 2)² = 32 (a (b x+2=9 x=7 Vx + 2 + 4 = 7 √√7+2+417 تحقق ✓ 7=7 Vx - 12 = 2 - Vi Vx - 12 = 2 - Vi (√x 12)2 (2-√x) 2 x - 12 = 4 - 4V + x -16 = -4V7 4=√x 16 = x المعادلة الأصلية اطرح 4 من الطرفين لفصل الجذر ربع الطرفين للتخلص من الجذر أوجد مربع الطرفين اطرح 2 من الطرفين المعادلة الأصلية عوض عن X بالعدد 7 بسط المعادلة الأصلية ربع الطرفين أوجد مربع الطرفين اطرح 4 + x من الطرفين لفصل الجذر اقسم الطرفين على 4 ربع الطرفين وزارة التعليم الدرس 7-4 حل المعادلات والمتباينات الجذرية 49 2024-1446

"Unsaved rax)=2- f(x)=√x-12 إرشادات للدراسة التحقق من الحل يمكنك استعمال الحاسبة البيانية للتحقق من حل المعادلة، مثل كل طرف من أطراف المعادلة الأصلية بيانيا، ثم ابحث عن نقاط التقاطع تحقق Vx - 12 = 2 - V V16 – 12 3 2 – V16 V42 - 4 2-2 يكون حل هذه المعادلة دخيلًا. والتمثيلان البيانيان للمعادلة 12 - y = x ، والمعادلة y = 2 - V لا يتقاطعان، وهذا يؤكد أنه لا يوجد حل حقيقي. تحقق من فهمك Vx + 15 = 5 + V (1 5 √x 2-1 (1A للتخلص من الجذر التربيعي ارفع العبارة الجذرية للأس ،2 وللتخلص من الجذر التكعيبي ارفع العبارة الجذرية للأس 3 مثال 2 حل معادلة جذر تكعيبي حل المعادلة : 0 = 4 - 3 (3 - 26 للتخلص من الأس } (الجذر التكعيبي) يجب أولا جعل المقدار المرفوع للأس ل في طرف لوحده، ثم رفع طرفي المعادلة للأس 3 2(6x-3)-4=0 - 33 = 4 2(6x-3)34 (6x-3)3 = 2 [(6x-3)³]³ =23 6x - 3 = 8 6x = 11 11 x = 6 المعادلة الأصلية أضف 4 للطرفين اقسم الطرفين على 2 كعب الطرفين أوجد مكعب الطرفين أضف 3 للطرفين اقسم الطرفين على 6 تحقق 0 = 4 - 33 - 26 المعادلة الأصلية عوض عن X بالعدد 11 6 وزارة التعليم Ministry of Education 2024-1446 بسط الجذر التكعيبي للعدد 8 هو 2 اطرح 2601 - 33 - -40 2(8)3-40 2(2)-40 ✓ 0=0 تحقق من فهمك 1 3(5y 1)3-2=0 (2B (3n+2)+10 (2A الفصل 4 العلاقات والدوال العكسية الجذرية 50 50

إرشادات الاختبار تعويض البدائل يمكنك أيضًا حل سؤال الاختبار بتعويض كل البدائل المعطاة لقيمة في المعادلة لاختيار الحل الصحيح منها وهو الذي يحقق المعادلة. يمكنك استعمال طرائق حل معادلات الجذور التربيعية والتكعيبية في حل المعادلات الجذرية أيا كان دليل جذرها. وللتخلص من الجذر النوني لأي عبارة ارفعه للأس . مثال 3 على اختبار ما حل المعادلة 0 = 6 - ( 6 + 2 )3 -1 A 1 B 3(√√2n+6)-6=0 3(√√2n+6)=6 √√2n+6=2 (√√2n+6)4=24 21 + 6 = 16 2n = 10 n = 5 11 D 5 إذن الجواب هو C. تحقق من فهمك المعادلة الأصلية أضف 6 للطرفين اقسم الطرفين على 3 ارفع الطرفين للأس 4 أوجد ناتج كل من الطرفين اطرح 6 من الطرفين اقسم الطرفين على 2 1 4(3x+6)412=0 (3 x=7A x = 37 D x = 29 C x = 25 B إرشادات الاختبار المتباينات الجذرية . بما أن الجذر التربيعي الرئيس لا يكون سالبا أبدا، فإن المتباينات التي تبسط إلى الصورة Vax + b حيث ) عدد سالب ليس لها حل، والتي تبسط إلى الصورة Vax + b c تكون مجموعة حلها هي مجموعة الأعداد الحقيقية. . إذا كان طرفا المتباينة موجبين، فإنه يمكنك تربيع الطرفين مع بقاء الرمز ك كما هو. حل المتباينات الجذرية : المتباينة الجذرية هي متباينة تحوي عبارات جذرية، ويكون المتغير فيها تحت الجذر. ولحلّ متباينة جذرية، اتبع الخطوات الآتية: مفهوم أساسي حل المتباينات الجذرية أضف إلى مطو الخطوة 1: إذا كان دليل الجذر عددًا ،زوجيًا، فعين قيم المتغير التي لا تجعل ما تحت الجذر ساليا. الخطوة 2 : حل المتباينة جبريًا. الخطوة 3 : حدد حل المتباينة من الخطوتين السابقتين، ثم اختبر القيم لتتأكد من صحة الحل. مثال 4 حل المتباينة الجذرية حل المتباينة: 8 ≥ 10 - 5x + 3 الخطوة 1: بما أن ما تحت الجذر التربيعي يجب أن يكون أكبر من أو يساوي صفرا، فحل أولًا 0 = 10 - 5x لتعين قيم المتغير x التي تجعل الطرف الأيسر من المتباينة معرّفا. 5x - 10>0 5x >10 x22 الخطوة 2 حل المتباينة 8 - 10 - 5x + 3 المعادلة الأصلية أضف 10 للطرفين اقسم الطرفين على 5 8 = 10 - V5x + المتباينة الأصلية √5x-10≤5 5x – 10 < 25 5x≤35 x ≤7 اطرح 3 من الطرفين لفصل الجذر ربع الطرفين للتخلص من الجذر أضف 10 للطرفين اقسم الطرفين على 5 وزارة التعليم الدرس 7-4- حل المعادلات والمتباينات الجذرية 51 2024-1446

يمكن استعمال طرائق حل معادلات الجذور التربيعية والتكعيبية في حل المعادلات الجذرية أيا كان دليل جذرها.

تعويض البدائل
حل المتباينة الجذرية
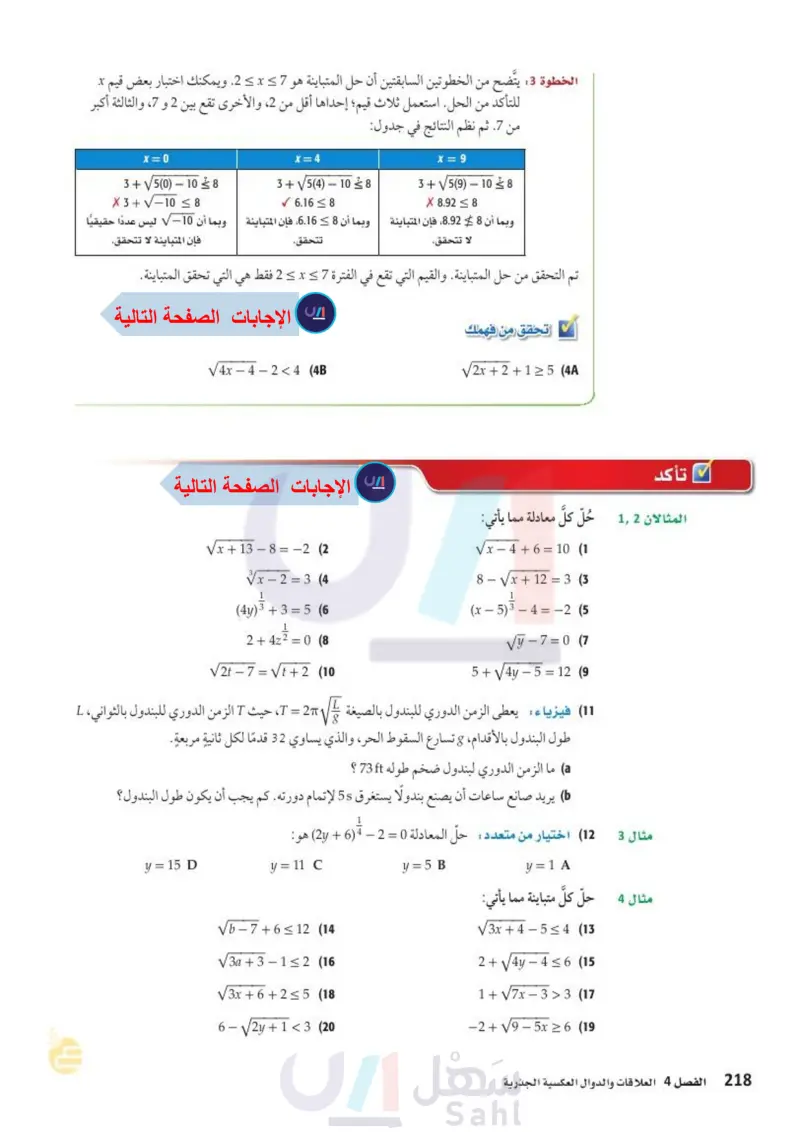
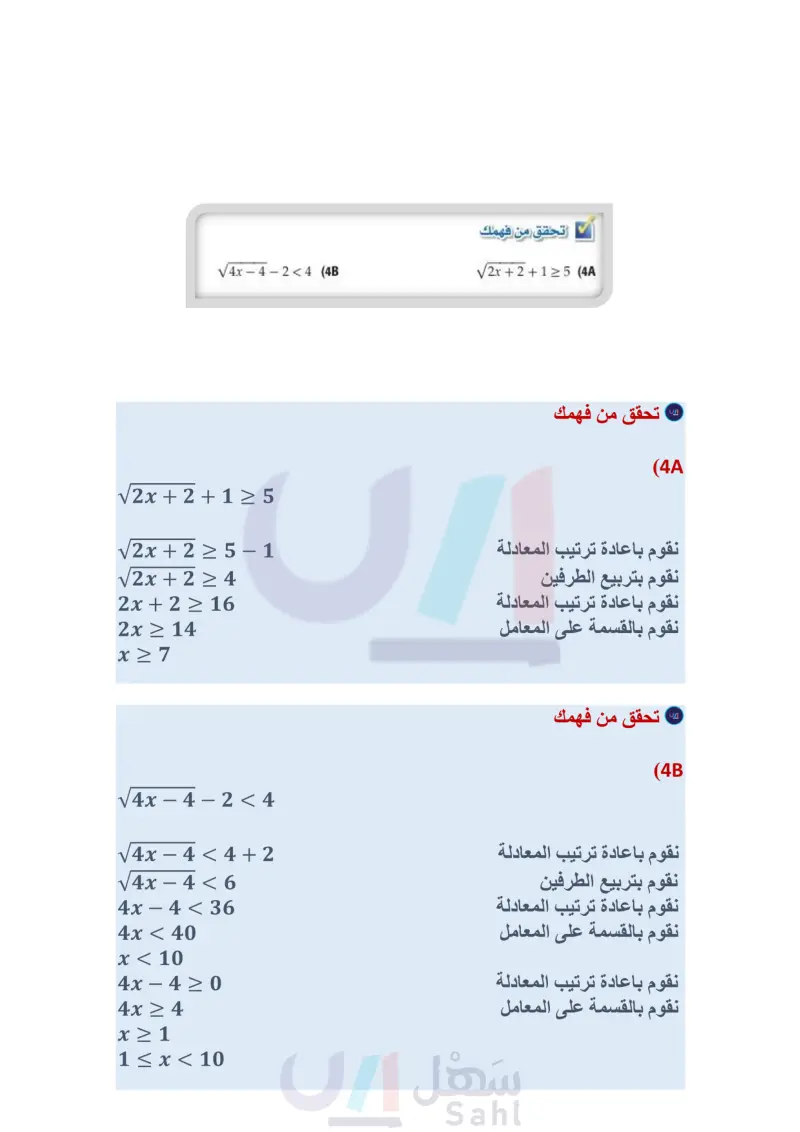
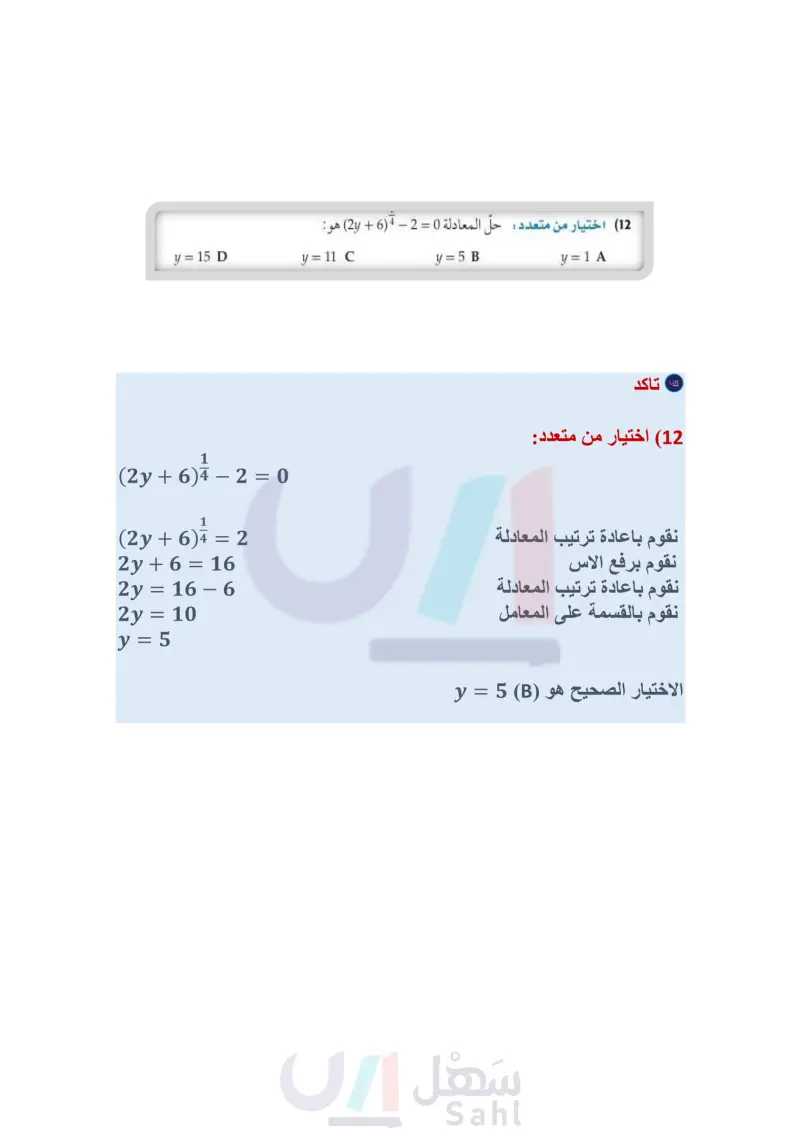
الخطوة 3: يتضح من الخطوتين السابقتين أن حل المتباينة هو 7 = x 2. ويمكنك اختبار بعض قيم x للتأكد من الحل. استعمل ثلاث قيم؛ إحداها أقل من 2 والأخرى تقع بين 2 و 7، والثالثة أكبر من 7. ثم نظم النتائج في جدول: x=0 3+5(0) X 3 + V-10 108 8 x=4 3+√√5(4)-108 ✓ 6.168 x = 9 3+√√5(9)-108 X 8.928 وبما أن V10 ليس عددًا حقيقيا وبما أن 8 6.16، فإن المتباينة وبما أن 8 8.92، فإن المتباينة لا تتحقق. تتحقق. فإن المتباينة لا تتحقق تم التحقق من حل المتباينة والقيم التي تقع في الفترة 7 = x = 2 فقط هي التي تحقق المتباينة. تحقق من فهمك √√4x-4-2<4 (4B √√2x+2+1≥5 (4A تأكد المثالان 1 حُلّ كل معادلة مما يأتي: Vx + 13 - 8 = -2 (2) √√√x-2=3 (4 (4)+3 (4y) 3 + 3 = 5 (6) 2 + 422 = 0 (8 √√√2t-7=√√t+2 (10 Vx - 4 + 6 = 10 (1 8 - Vx + 12 = 33 1 (x-5)3-4=-2 (5 √y-7=0 (7 5 + V4y - 5 = 12 (9 11) فيزياء : يعطى الزمن الدوري للبندول بالصيغة 27 = T ، حيث T الزمن الدوري للبندول بالثواني، L طول البندول بالأقدام، 8 تسارع السقوط الحر، والذي يساوي 32 قدما لكل ثانية مربعة. g a ما الزمن الدوري لبندول ضخم طوله ft 73 ؟ ) يريد صانع ساعات أن يصنع بندولا يستغرق 55 لإتمام دورته كم يجب أن يكون طول البندول؟ 1 (12) اختيار من متعدد حلّ المعادلة 0 = 2 - 7 (6 + 2) هو : مثال 3 y=1A مثال 4 حل كل متباينة مما يأتي: y=5 B y = 15 D y= 11 C وزارة التعليم Ministry of Education 2024-1446 √b-7+6≤12 (14 V3 + 3 - 152 (16) V3x + 6 + 2 < 5 (18 6 2y+1<3 (20 V3x + 4 - 554 (13) 2 + 4y - 4 5 6 (15) 1+V7x-3>3 (17 -2+√√9-5x≥6 (19 الفصل 4 العلاقات والدوال العكسية الجذرية 52

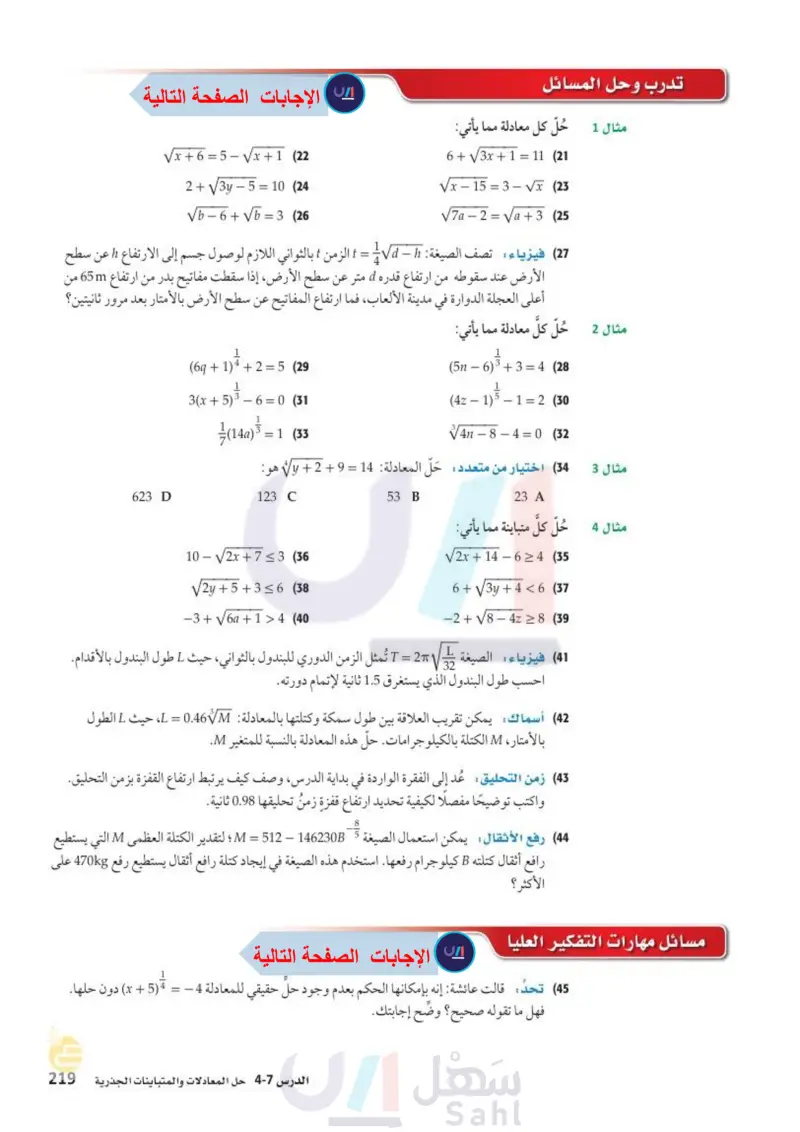
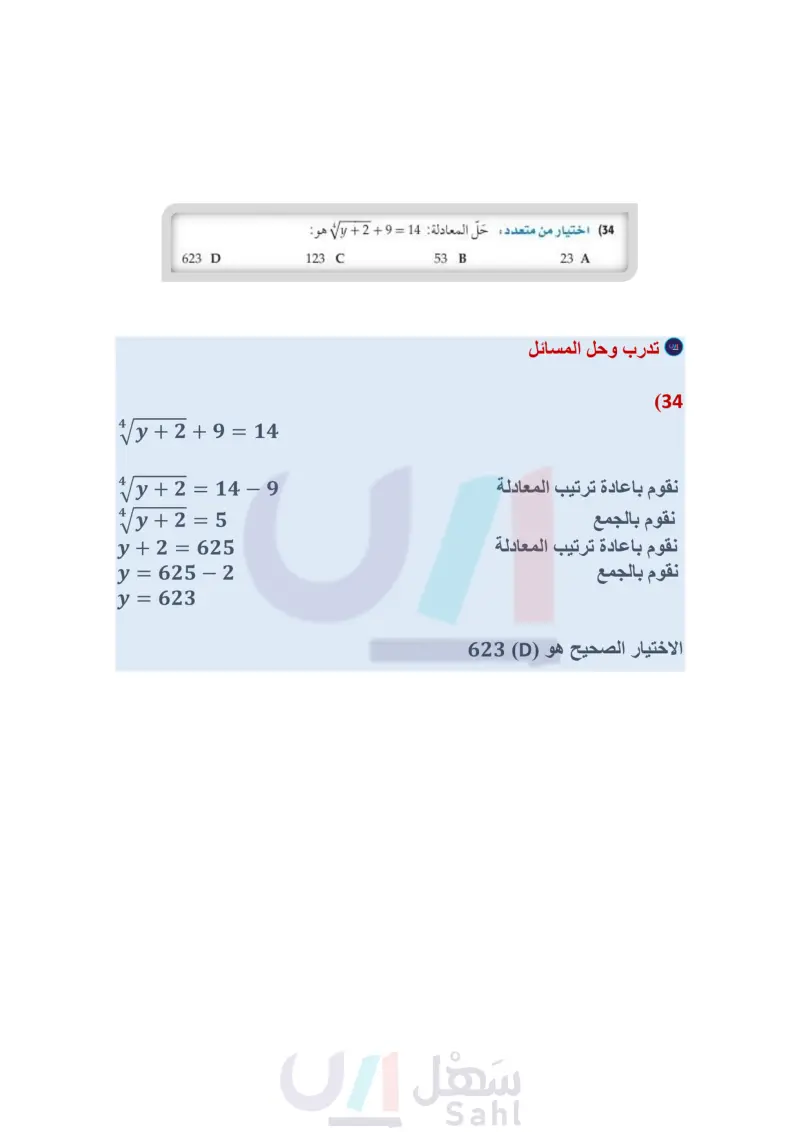
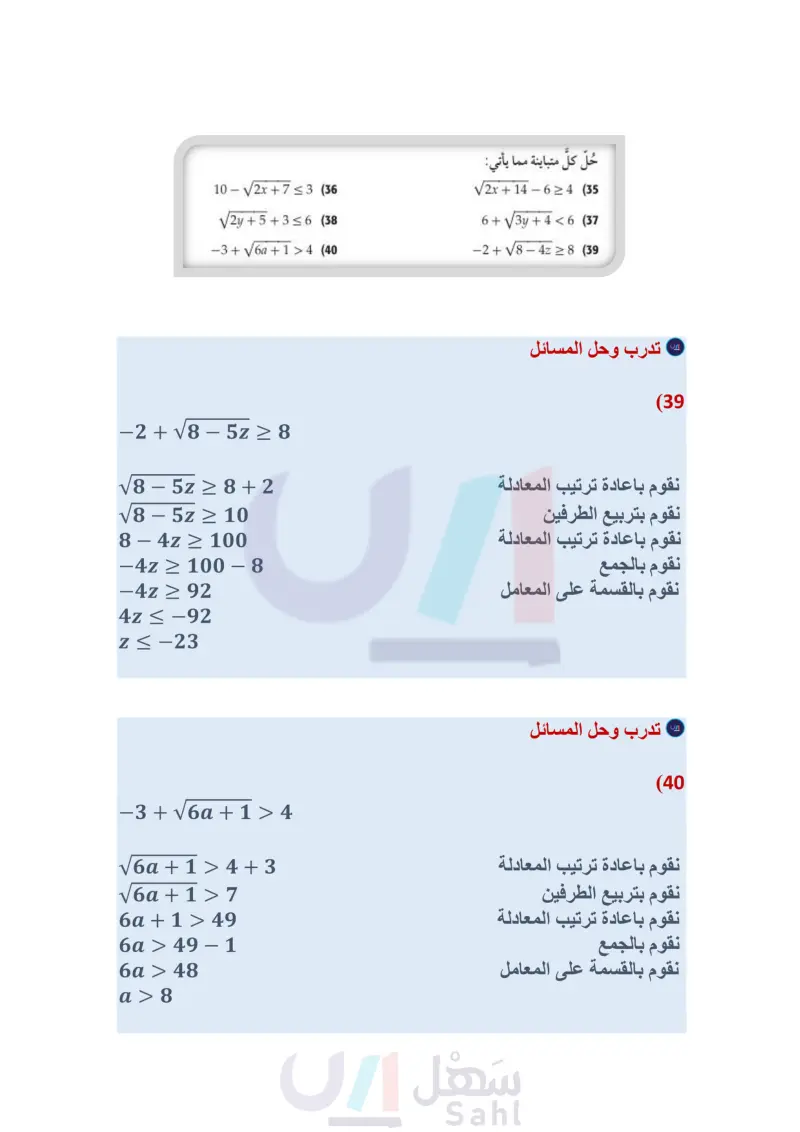
تدرب وحل المسائل مثال 1 حُلّ كل معادلة مما يأتي: Vx + 6 = 5 - Vx + 1 (22) 6 + V3x + 1 = 11 (21 2 + 3y - 5 = 10 (24) V6 - 6 + V = 3 (26) Vx - 15 = 3 - V (23) V7a - 2 = a + 3 (25) t= (27) فيزياء : تصف الصيغة : Vah = الزمن بالثواني اللازم لوصول جسم إلى الارتفاع عن سطح الأرض عند سقوطه من ارتفاع قدره d متر عن سطح الأرض ، إذا سقطت مفاتيح بدر من ارتفاع 65m من أعلى العجلة الدوارة في مدينة الألعاب، فما ارتفاع المفاتيح عن سطح الأر بالأمتار بعد مرور ثانيتين؟ مثال 2 حُلّ كل معادلة مما يأتي: (6 + 1) 4 + 2 = 5 (29) 3(x+5)3 6 0 (31 (140) = 1 = 1 (33 623 D 123 C (5n 6)3+3 4 (28 (4z 1)5 1 2 (30 4 - 8 - 4 = 0 (32) مثال 3 (34) اختيار من متعدد حَلّ المعادلة : 14 = 1 + 2 + y هو : 23 A مثال 4 حُلّ كل متباينة مما يأتي: 53 B 10 √√2x+7≤3 (36 2y + 5 + 3 = 6 (38 -3+√√6a+1>4 (40 V2x + 14 - 6 24 (35) 6+3y+4<6 (37 -2+V8 4z≥8 (39 L 32 41) فيزياء الصيغة 27 = T تمثل الزمن الدوري للبندول بالثواني، حيث L طول البندول بالأقدام. احسب طول البندول الذي يستغرق 1.5 ثانية لإتمام دورته. (42) أسماك: يمكن تقريب العلاقة بين طول سمكة وكتلتها بالمعادلة : L = 0.46M، حيث L الطول بالأمتار، M الكتلة بالكيلوجرامات . حلّ هذه المعادلة بالنسبة للمتغير M. (43) زمن التحليق : عُد إلى الفقرة الواردة في بداية الدرس، وصف كيف يرتبط ارتفاع القفزة بزمن التحليق. واكتب توضيحًا مفصلا لكيفية تحديد ارتفاع قفزة زمن تحليقها 0.98 ثانية. (44) رفع الأثقال: يمكن استعمال الصيغة 5 1462303 - 512 = M ؛ لتقدير الكتلة العظمى M التي يستطيع رافع أثقال كتلته B كيلو جرام رفعها. استخدم هذه الصيغة في إيجاد كتلة رافع أثقال يستطيع رفع 470kg على الأكثر ؟ مسائل مهارات التفكير العليا 1 45) تحد قالت عائشة : إنه بإمكانها الحكم بعدم وجود حلّ حقيقي للمعادلة 4 – = (5 + x) دون حلها. فهل ما تقوله صحيح؟ وضح إجابتك. وزارة التعليم الدرس 7-4 حل المعادلات والمتباينات الجذرية 53 2024-1446

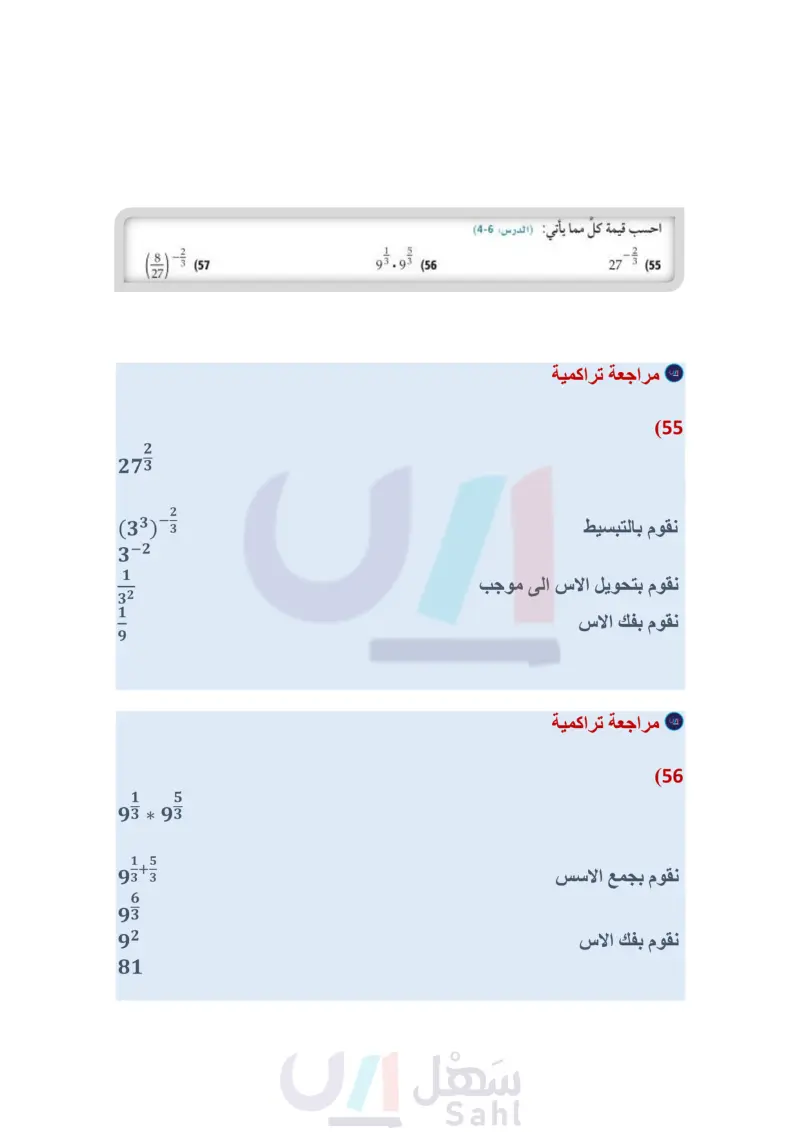
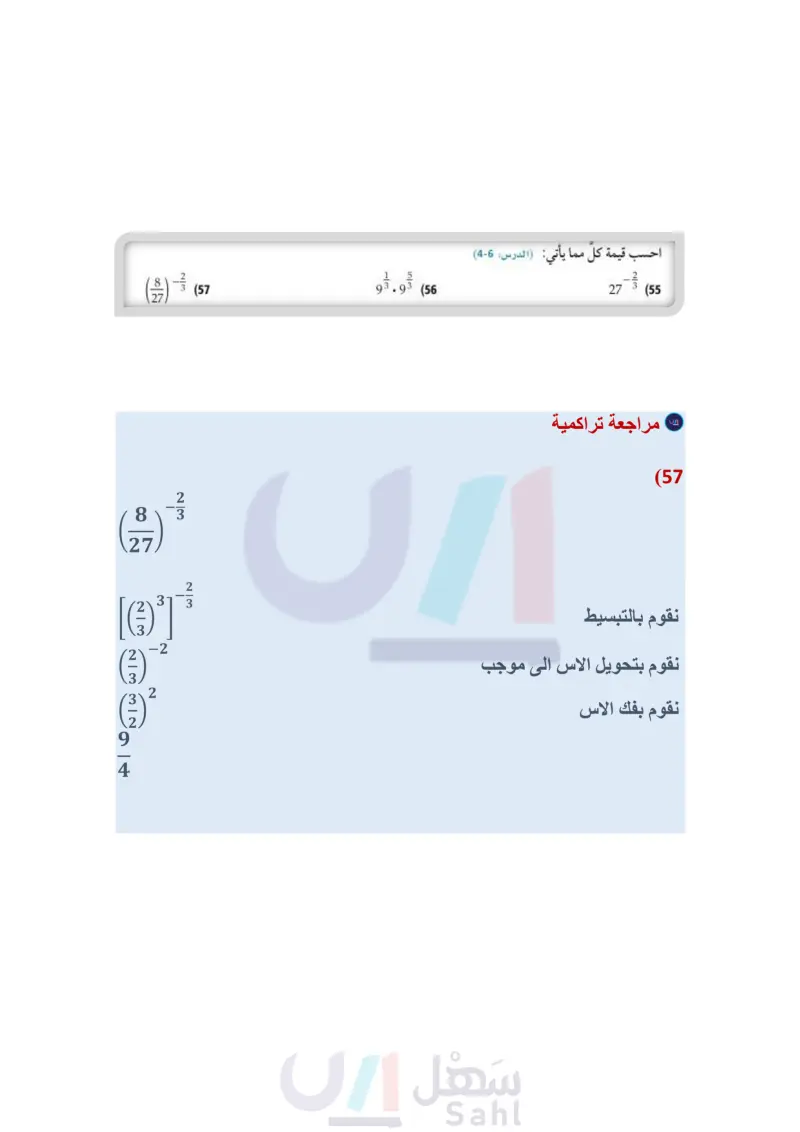
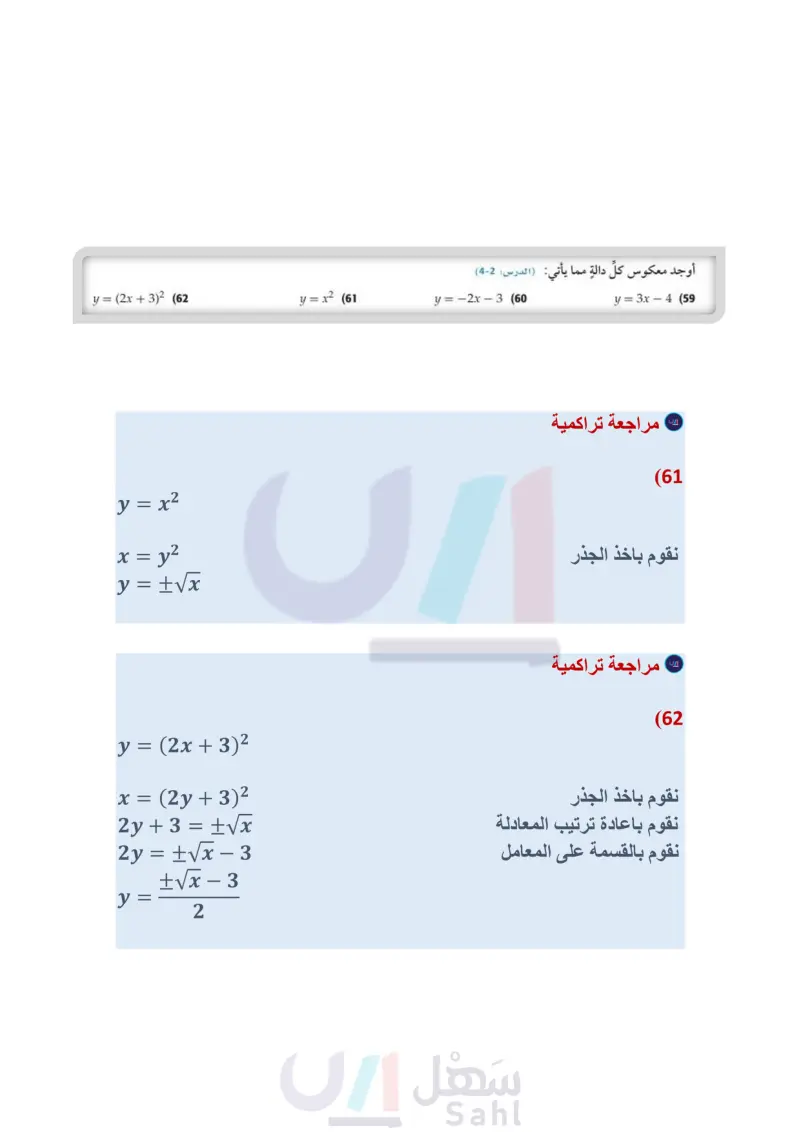
Vx + 1 + 3 = 4 Vx + 2 - 7 = -10 (46) أي معادلة مما يأتي ليس لها حل؟ Vx - 1 + 3 = 4 Vx - 2 + 7 = 10 تدريب على اختبار √(x2)2 (47) تبرير حدد ما إذا كانت . = x ، صحيحة دائمًا ، أو صحيحة أحيانًا ، أو غير صحيحة أبدًا، وذلك إذا كان x عددًا حقيقيا. ووضّح إجابتك. 48) مسألة مفتوحة : اختر عددًا كليًّا، واعمل بشكل عكسي لكتابة معادلتين جذريتين يكون حلّهما ذلك العدد الكلي، بحيث تكون إحداهما معادلة جذر تربيعي، والأخرى معادلة جذر تكعيبي. (49) مسألة مفتوحة : اكتب معادلة يمكن حلّها برفع كلا الطرفين للأس المعطى : (b 50) تحد: حَلّ المعادلة : 1 + 73x - 1 = 49x. (إرشاد : b = by إذا وفقط إذا كان x = y ) . (51) اكتب وضّح العلاقة بين دليل جذر المتغير في المعادلة الجذرية والأس الذي ترفع طرفي المعادلة له عند حلها. (52) أي المجموعات الآتية تمثل دالة؟ (53) إجابة قصيرة محيط مثلث متطابق الضلعين 56in. فإذا كان طول أحد الضلعين المتطابقين 20in ، فما طول الضلع الثالث؟ (54) ما حل المعادلة 4 = 1 + 5 + x ؟ 20 D 11 C 10 B 4 A {(3,0), (-2,5), (2, -1), (2,9)} A {(-3, 5), (-2,3), (-1,5), (0,7)} B {(2,5), (2, 4), (2, 3), (2, 2)} C {(3, 1), (-3, 2), (3, 3), (-3, 4)} D مراجعة تراكمية احسب قيمة كل مما يأتي: (الدرس: 6-4) 27-3 (55) 93.93€ (56) (3) - (57 58) هندسة : العبارتان 4x2y28x2y2. تمثلان طولي ساقي الزاوية القائمة في مثلث قائم الزاوية، أوجد عبارةً ثالثة تمثل طول الوتر باستعمال نظرية فيثاغورس، ثم بسطها. الدرس : 6-4) أوجد معكوس كل دالة مما يأتي: (الدرس (2-4) y=3x-4 (59 y= -2x-3 (60 حلّ كل معادلة مما يأتي واكتب الحل في أبسط صورة: (مهارة سابقة) y = (2x + 32 (62) y = x2 (61 وزارة التعليم Ministry of Education 2024-1446 p = (66 = 18 (65 =9m (64 = a (63) الفصل 4 العلاقات والدوال العكسية الجذرية 54




 0
0 
 0
0 
 0
0 

 0
0