تشابه المضلعات - الرياضيات 1 - ثاني متوسط
الفصل1: الأعداد النسبية
الفصل2: الأعداد الحقيقية ونظرية فيثاغورس
الفصل3: التناسب والتشابه
نشاط الفصل1: الأعداد النسبية
نشاط الفصل2: الأعداد الحقيقية ونظرية فيثاغورس
۱۲۸ ٣-٦ تشابه المضلعات رابط الدرس الرقمي www.ien.edu.sa فكرة الدرس أعين المضلعات المتشابهة، وأجد القياسات الناقصة فيها. المفردات المضلع. المضلعات المتشابهة. الأجزاء المتناظرة. التطابق. عامل المقياس. نشاط نفذ الخطوات الآتية لاكتشاف العلاقة المثلثات : الخطوة ( انسخ كلا المثلثين على ورق شفاف. الخطوة ٢ قس أطوال أضلاع كل مثلث وسجّلها. الخطوة 3 قص كلا المثلثين. 1 قارن بين زوايا المثلثين بالمقابلة. بین وعين أزواج الزوايا التي لها القياس نفسه. أب ب ج i عبّر عن النسب الآتية: دهـ ه و جـأ ود أ و في صورة كسور عشرية إلى أقرب جزء من عشرة. 3. ماذا تلاحظ على النسب بين أطوال الأضلاع المتقابلة في المثلثين؟ يتكون المضلع من مجموعة من القطع المستقيمة في مستوى، متقاطعة في نهاياتها، بحيث تكون شكلًا مغلقا. وتسمى المضلعات التي لها الشكل نفسه مضلعات متشابهة . ففي الشكل أدناه يشبه المضلع أب جــد المضلع هـ وزح ، ويعبّر عن ذلك بالرموز كما يأتي: المضلع أب جـد - المضلع هـ و زح. ح و جے د تسمى الأجزاء المتقابلة في الأشكال المتشابهة أجزاء متناظرة. د الفصل :: التناسب والتشابه ز ح الزوايا المتناظرة دأ اهـ ، ا ب » دو لجلز، لدل. د و ز ح الأضلاع المتناظرة 6 6 زح ، اد هـح وزارة التعليم Ministry of Education 2024-1446

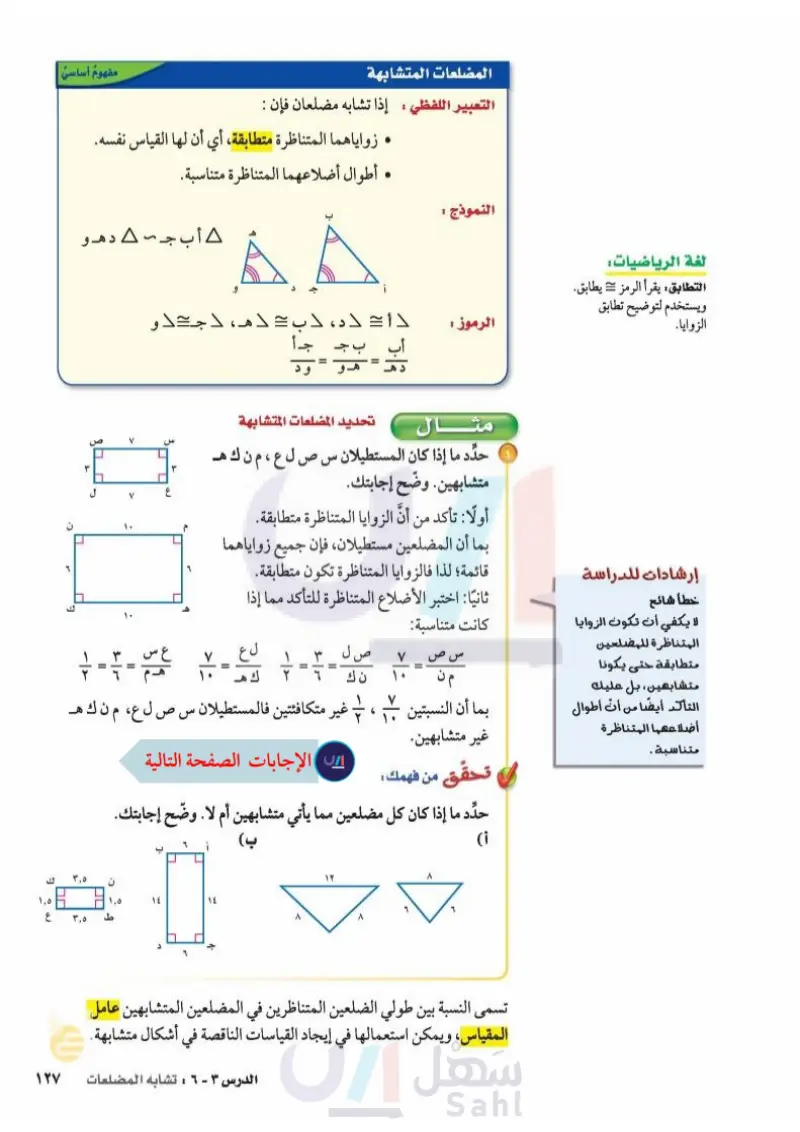
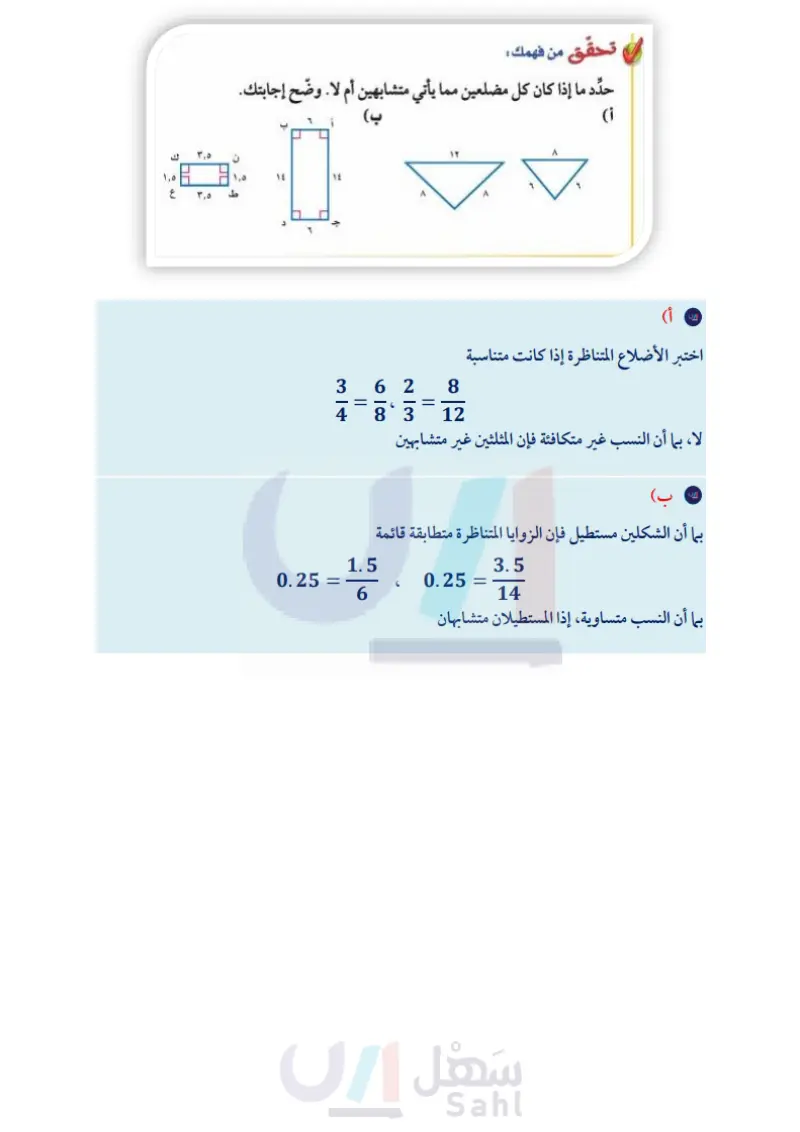
لغة الرياضيات المضلعات المتشابهة التعبير اللفظي : إذا تشابه مضلعان فإن : مفهوم أساسي زوایاهما المتناظرة متطابقة، أي أن لها القياس نفسه. . أطوال أضلاعهما المتناظرة متناسبة. النموذج أ ب ج - 4 دهـو التطابق : يقرأ الرمز = يطابق. ويستخدم لتوضيح تطابق الزوايا. الرموز : دأ = ده، لب = هـ، لج= دو جـد أ ود مثال تحديد المضلعات المتشابهة V إرشادات للدراسة خطأ شائح لا يكفي أن تكون الزوايا المتناظرة للمضلعين متطابقة حتى يكونا متشابهين، بل عليك التأكد أيضًا من أن أطوال أضلاعهما المتناظرة متناسبة. حدد ما إذا كان المستطيلان س ص ل ع ، م ن ك هـ متشابهين. وضّح إجابتك. أولا : تأكد من أنَّ الزوايا المتناظرة متطابقة. بما أن المضلعين مستطيلان، فإن جميع زواياهما قائمة ؛ لذا فالزوايا المتناظرة تكون متطابقة. ثانيًا : اختبر الأضلاع المتناظرة للتأكد مما إذا كانت متناسية : بما أن النسبتين غير متشابهين. تحقق من فهمك : ص ل ن ك = له ع V ۱۰ = = ل ٦ 勺 غير متكافئتين فالمستطيلان س ص ل ع، م ن ك هـ حدد ما إذا كان كل مضلعين مما يأتي متشابهين أم لا . وضح إجابتك. أ) ب) أ جا Λ ۱۲ ١٤ ١٤ 2 JL ط E ٣,٥ ٣,٥ له ع تسمى النسبة بين طولي الضلعين المتناظرين في المضلعين المتشابهين عامل المقياس، ويمكن استعمالها في إيجاد القياسات الناقصة في أشكال متشابهة . الدرس ٣ - ٦ : تشابه المضلعانارة التو٢ ليم Ministry of Education 2024-1446

۱۳۰ لغة الرياضيات : طول القطعة المستقيمة يكتب طول دأ على النحود أ، والذي يعبر عن قيمة عددية. مثال إيجاد القياسات الناقصة هندسة : إذا كان المضلع ف روش - أب جـد ، فأوجد ر الطريقة الأولى كتابة تناسب رو. افترض أن م هي قيمة طول رو. اكتب تناسبا : المضلع فروش > المضلع أب جـد » و 1: = f ۱۰ ۱۳ ۱۲ د المضلع فروش المضلع أب جـد رو = م ، ب ج = ۱۲ ، و ش = ١٥ ، ج د = ١٠ م × 10 = ١٢ × ١٥ اضرب ضربًا تبادليًّا. ۱۰ م = ۱۸۰ أوجد ناتج الضرب. م = ۱۸ اقسم كلا الطرفين على ١٠ . ٢٤ و ۱۵ إرشادات للدراسة عامل المقياس في المثال ؟ عامل المقياس من المضلح أب جد إلى الطريقة الثانية استعمال عامل المقياس في كتابة معادلة . ١٥ أوجد عامل المقياس بين المضلعين فروش، أب جد. وش عامل المقياس : عامل المقياس هو ثابت التناسب. المضلح ف روش هوا " التعبير وهذا يعني أن الطول على اللفظي المضلح أ ب جـد يساوي - ۲ من الطول على المضلح ف المتغيّر طول الضلع في المضلع ف ر وش يساوي - طول الضلع المناظر له في المضلع أب جـد لتكن م تمثل طول رو روش. المعادلة م = ٣ ۱۲ الفصل :: التناسب والتشابه م = = × ۱۲ اكتب المعادلة. م = ۱۸ اضرب. اختر طريقتك أوجد القياسات الناقصة في المثال (۲) أعلاه: جـ ) ف ش د ) أب إذا كان المربع أ - المربع ،ب، وعامل المقياس بينهما يساوي ٣ : ٢، فإن النسبة بين طولي محيطي المربعين تساوي ١٢ : ٨ = ۳ : ۲ م ۲ م المربع أ المربع ب المحيط المربع أ ۱۲ م ام و ش وزارة التعليم Ministry of Education 2024-1446

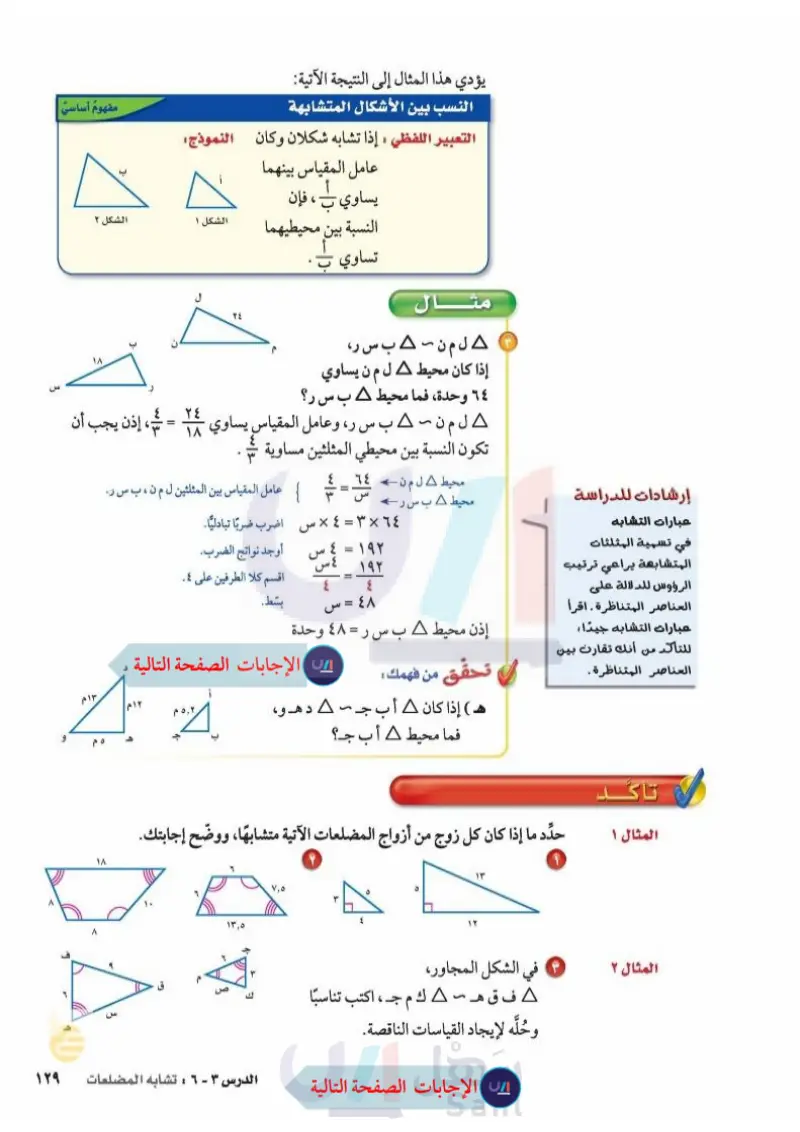
يؤدي هذا المثال إلى النتيجة الآتية: النسب بين الأشكال المتشابهة التعبير اللفظي : إذا تشابه شكلان وكان النموذج عامل المقياس بينهما يساوي ، فإن النسبة بين محيطيهما تساوي . : مفهوم أساسي الشكل 1 الشكل ٢ 3 ٢٤ مثال إرشادات للدراسة عبارات التشابه في تسمية المثلثات المتشابهة يراعي ترتيب الرؤوس للدلالة على العناصر المتناظرة . اقرأ عبارات التشابه جيدًا؛ للتأكد من أنك تقارن بين العناصر المتناظرة. ل م ن - ح ب س ر، إذا كان محيط A ل م ن يساوي ٦٤ وحدة، فما محيط A ب س ر ؟ ٢٤ ١٨ ل م ن - ج ب س ر، وعامل المقياس يساوي 1 = ، إذن يجب أن ٤ تكون النسبة بين محيطي المثلثين مساوية . ٦٤ ۱۸ ل م ن = عامل المقياس بين المثلثين ل م ن ، ب س ر . محيط ٥ - محیط A ب س ر - { ٦٤ × 3 = 4 × س اضرب ضربًا تبادليًّا. ۱۹۲ ٤ = ۱۹۲ ٤ || أوجد نواتج الضرب. س س ٤ ٤٨ = س إذن محيط A ب س ر = ٤٨ وحدة تحقق من فهمك : اقسم كلا الطرفين على ٤. بسط . هـ ( إذا كان A أب جـ - 4 دهـ و، فما محيط A أب جـ ؟ د ۱۳م ۱۲م ه م ٨ س تأكد المثال ۱ حدد ما إذا كان كل زوج من أزواج المضلعات الآتية متشابها، ووضح إجابتك. ٦ 13,5 تشابه المضلعات وزارة التسليم الدرس 3 - Ministry of Education 2024-1446 ٢ ٤ ۱۲ ۱۳ T المثال ٢ في الشكل المجاور، A ف ق هـ - ٥ ك م ج ، اكتب تناسبًا وحُلَّه لإيجاد القياسات الناقصة.

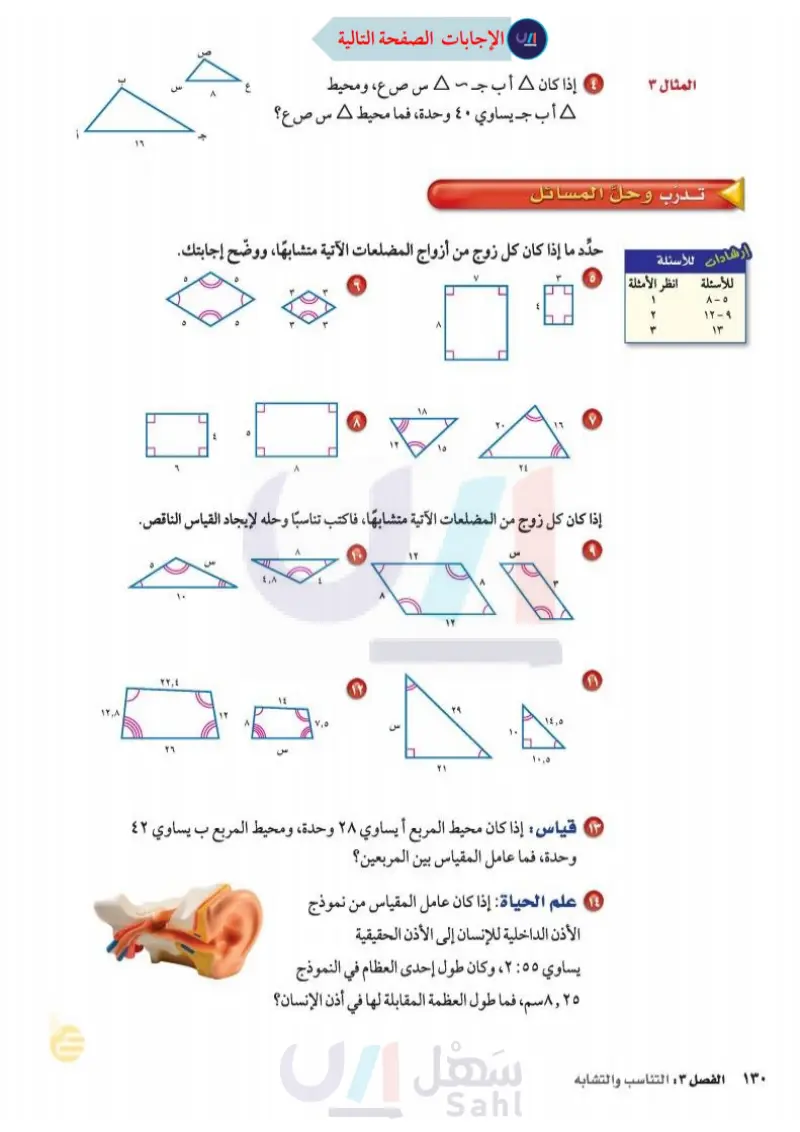
أ ۱۲,۸ وزارة التعليم Ministry of Education 2024-1446 3 Z. Λ إذا كان 4 أب جـ - A س صع، ومحيط A أب جيساوي ٤٠ وحدة، فما محيط A س صع؟ المثال ٣ تدرب وحل المسائل إرشادات للأسئلة للأسئلة انظر الأمثلة حدد ما إذا كان كل زوج من أزواج المضلعات الآتية متشابها، ووضّح إجابتك. ٦ ۱۸ ۱۲ ١٥ ٢٤ ܖܙ V إذا كان كل زوج من المضلعات الآتية متشابها، فاكتب تناسبًا وحله لإيجاد القياس الناقص. س ۱۲ س ٢٢,٤ ٢٦ ۱۲ Λ ٤,٨ ٤ Λ س ۱۲ س ۱۲ Λ ۲۹ 18,0 10,5 ٢ قياس : إذا كان محيط المربع أيساوي ۲۸ وحدة، ومحيط المربع ب يساوي ٤٢ وحدة، فما عامل المقياس بين المربعين؟ 18 علم الحياة : إذا كان عامل المقياس من نموذج الأذن الداخلية للإنسان إلى الأذن الحقيقية يساوي ٥٥ : ٢ ، وكان طول إحدى العظام في النموذج ٨,٢٥ سم ، فما طول العظمة المقابلة لها في أذن الإنسان؟ 1 - O ۲ ۱۲ - ۹ ۱۳ الفصل :: التناسب والتشابه ۱۳۲

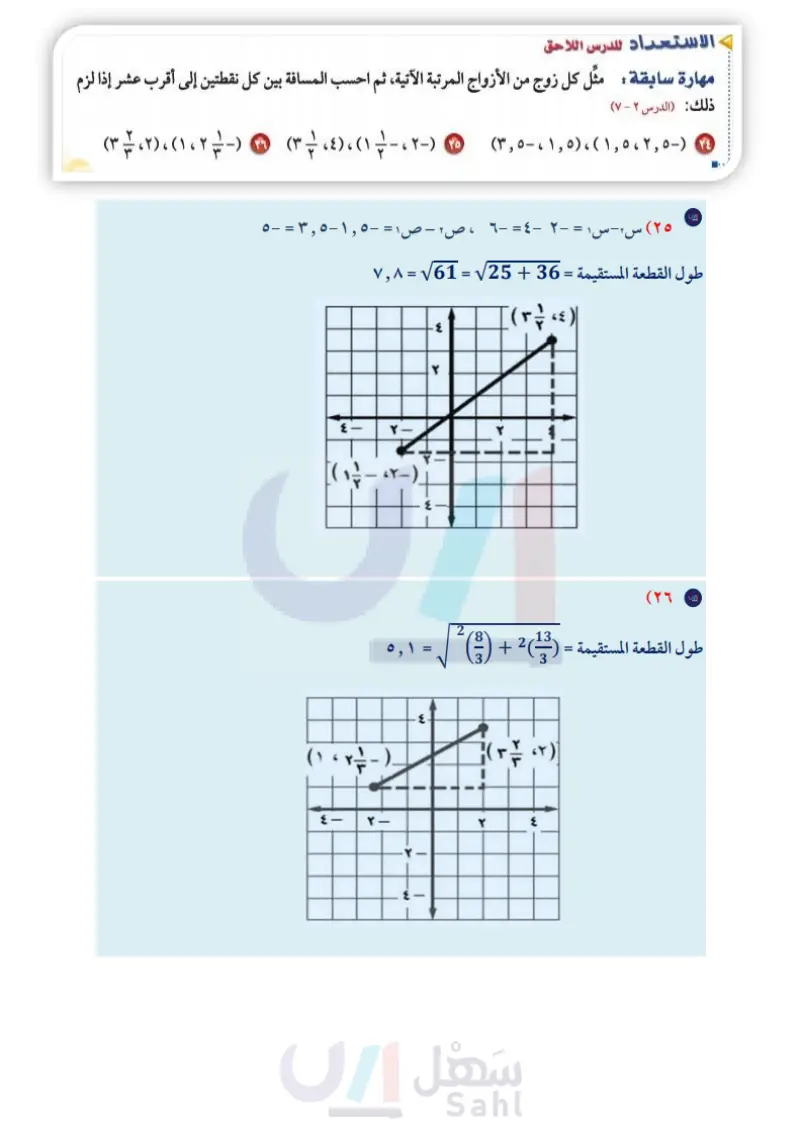
مسائل مهارات التفكير العليا ٥ تحد : افترض أن مستطيلين متشابهان بعامل مقياس مقداره ۲ ، فما النسبة بين مساحتيهما؟ وضح إجابتك. اكتب حدد ما إذا كانت كل عبارة مما يأتي صحيحة دائماً أم أحياناً أم غير صحيحة أبدًا. ووضّح إجابتك. ١٦ كل مستطيلين متشابهان. م تدريب على اختبار ٧ كل مربعين متشابهان. إذا كان 4 أ ب جـ - A س ص ع فما طول صع؟ ١٩ إذا كان المضلع أب جـد يشابه المضلع فروش ، وكان محيط المضلع أب جــد يساوي ٥٤ م، فما ۲۷ ٣٦ ۱۸ سم محيط المضلع فروش؟ أ) سم -12212 ٣٤ سم د ۱۳سم ۲۲سم جـ) ٢٤ سم د) ٥,٢٥ سم ب) ٢٤ م جـ) ۲۷ م د) ٣٦م معة تراكمية تسلق جبال يهوى أحمد تسلق الجبال، ولكي يصل إلى قمة الجبل يتبقى له ٣٠ قدماً، إذا كان يصعد ٦ أقدام في كل ٥ دقائق، ولكنه يتعثر فينزل قدمًا واحدة، ويستغرق دقيقة واحدة لاستعادة توازنه واستئناف الصعود، فكم دقيقة يستغرق أحمد حتى يبلغ قمة الجبل؟ (استعمل استراتيجية الرسم) (الدرس ٣ - ٥) حل كل تناسب مما يأتي : (الدرس ٣ - ٤) = ۱۲ ٢٤ = 아 || الاستعداد للدرس اللاحق مهارة سابقة : مثل كل زوج من الأزواج المرتبة الآتية، ثم احسب المسافة بين كل نقطتين إلى أقرب عشر إذا لزم ذلك: (الدرس ۲ - ۷ ۳ (۳ ، ۲) ،(۱،۲) (۳) ، ١( ، )٤ - - ، ۲-) (۱ (x, 0-61,0). (1,00Y, O-) YE تشابه المضلعا نوارة الت٣٣ليم الدرس 3 - Ministry of Education 2024-1446

يهوى أحمد تسلق الجبال ولكي يصل إلى قمة الجبل يتبقى له30 قدما إذا كان يصعد ٦ أقدام في كل ٥ دقائق ولكنه يتعثر فينزل قدما واحدة ويستغرق دقيقة واحدة لاستعادة توازنه واستئناف الصعود فكم دقيقة يستغ




 0
0 

 0
0 

 0
0 

 0
0