تمثيل دوال المقلوب بيانيا - رياضيات2-2 - ثاني ثانوي

www.ien.edu.sa تمثيل دوال المقلوب بيانيًّا Graphing Reciprocal Functions 5-3 فيما سبق: درست تمثیل دوال كثيرات الحدود بيانيا. (مهارة سابقة) والان . أحدد خصائص دوال المقلوب . أمثل تحويلات دوال المقلوب بيانيا. المفردات: خط التقارب asymptote خط التقارب الرأسي vertical asymptote خط التقارب الأفقي لماذا؟ خططت . رعة من الطلبة لجمع مبلغ 5000 ريال للقيام بعمل خيري، فقرروا أن يتبرع كل منهم بريال واحد يوميًا، فإذا كان عدد الطلاب 11 طالبًا، فإن عدد الأيام ، اللازمة لجمع المبلغ يُعطى بالعلاقة . .C= 5000 n خطوط التقارب الرأسية والأفقية خط التقارب لدالة: هو مستقيم يقترب منه التمثيل البياني للدالة. ولدالّة المقلوب = (f(x خط تقارب رأسي عند القيمة المستثناة من مجالها، وخط تقارب أفقي يبين سلوك طرفي التمثيل البياني للدالة. مفهوم أساسي a(x) خطوط التقارب للدالة c + = 4 x-b أضف إلى مطويتك التعبير اللفظي للدالة y = + c ، 0 خط تقارب رأسي عند قيمة x التي تجعل المقام صفرا، =a x-b أي أن خط التقارب الرأسي للدالة هو x = b ، ويكون لها خط تقارب أفقي عند y = C . y √y= M 10 x-2 مثال: + وأما مجال الدالة ) . م = لا فهو جميع ا الأعداد الحقيقية ما عدا x = b ، وأما مداها فهو جميع الأعداد الحقيقية ما عدا y = c، ولأنه لا يمكن رسم هذه الدالّة دون رفع القلم عن الورقة؛ لذا اختر قيمًا لـ x على جانبي خط التقارب الرأسي لترسم جزأي منحنى الدالة. تمثل الدالة 2 = c دالّة مقلوب، ودالّة المقلوب التي سندرسها هيا الدالة المكتوبة على الصورة 1 5000 " = (f(x ، حيث (a(x دالة خطية، و 0 (a(x . مفهوم أساسي الدالة الرئيسة (الأم) لدوال المقلوب أضف إلى طويتك f(x) f(x)=1, x+0 f(x) = x الدالة الرئيسة (الأم): شكل التمثيل البياني المجال والمدى خطا التقارب قطع زائد جميع الأعداد الحقيقية ما عدا الصفر 0 = x و 0 = y المقطعان : لا يوجد تكون الدالة غير معرفة عندما : x=0 وزارة التعليم الدرس 3-3- تمثيل دوال المقلوب بيانيا 85 2024-1446 horizontal asymptote دالة المقلوب reciprocal function القطع الزائد hyperbola

-f(x)T -81 -6+ مجال دالة المقلوب هو مجموعة القيم التي تكون الدالة عندها معرفة. فمثلا الدوال = (f(x h(x) = g(x) = x+5 x=0 x=5 x = -2 غير معرفة عندما : مثال 1 القيود على المجال (تحديد القيم التي تجعل الدالة غير معرفة ) حدد قيمة x التي تجعل الدالة = 2 = (f(x غير معرفة. 2x+5 أوجد قيمة x التي يساوي المقام عندها صفرا. 20 6 8 x f(x)=3x+2 (1B .x= 2x + 5 = 0 x=- الدالة غير معرفة عندما تحقق من فهمك f(x) = 21 (۱ قد لا تكون بعض قيم x في دالّة المقلوب منطقية، وذلك في مسائل من واقع الحياة. فعلى سبيل المثال في التمثيل البياني المجاور، إذا كانت قيم x تمثل زمنا، أو مسافة أو عدد أشخاص فلا يمكن أن تكون هذه القيم سالبة في سياق المسألة، ولذلك لا حاجة للجزء الأيسر من التمثيل البياني والذي تكون فيه قيم x سالبة. مثال 2 من واقع الحياة تمثيل دالة المقلوب بيانيا سفر مثل الدالة 2 = (f(x بيانيا، حيث تمثل x عدد الأشخاص في منطاد هوائي، و ني، وتمثل (f(x متوسط المساحة المخصصة لكل شخص بالأقدام المربعة. بما أن عدد الأشخاص لا يكون صفرًا أو سالبا، عدد الأشخاص x 10 5 4 2 2 4 5 لذا استعمل الأعداد الصحيحة الموجبة فقط للمتغير x . المساحة المخصصة للشخص (f(x 10 (10, 2) (5, 4) (4, 5).(2, 10) bla المستوى الإحداثي وصل بينها بخط منحن. وبما أن الدالة غير معرفة عند (0=x)، فإن لها خط تقارب رأسي هو 0 = x؛ أي أن منحناها يقترب من المستقيم 0 = x (المحور y) ولا يمسه وبالمثل للدالة خط تقارب أفقي 0 = y (المحور x)؛ أي أن منحناها يقترب من المستقيم 0 = y ولا يمسه، لذا مُد المنحنى الذي رسمته في اتجاه كل من المحورين x y الموجبين، ولكن دون أن يمس أيا منهما، كما هو مبين في الشكل المجاور. تحقق من فهمك -20- 16- 12- 18+ +4 O 4 8 12 16 20 24: 8 (2) حدائق حديقة مستطيلة الشكل مساحتها cm2 18 ، والدالة = 1 تبين العلاقة بين طولها وعرضها. مثل هذه الدالة بيانيا. وزارة التعليم Ministry of Education 2024-1446 الفصل 5 العلاقات والدوال النسبية 86

مثال 3 تحديد خصائص دوال المقلوب حدد خطوط التقارب والمجال والمدى لكل من الدالّتين الآتيتين: +f(x) 2 f(x)= حدد قيمة x التي تكون الدالة (f(x عندها غير معرفة. x - 3 = 0 x=3 (f(x غير معرفة عند 3 = x . وهذا يعني وجود خط تقارب رأسي عند 3 = x ، وبما أن 0 = c فإنه، يوجد خط تقارب أفقي عند 0 = y (لاحظ أنه كلما زادت قيم x الأكبر من 3، تقترب قيم (f(x من الصفر، وكلما قلت قيم x الأقل من 3، تقترب قيم (f(x من الصفر أيضًا. وهذا يعني وجود خط تقارب أفقي عند 0 = y ) . جميع الأعداد الحقيقية ما عدا 3 . أما المدى فهو جميع الأعداد الحقيقية ما عدا الصفر. مجال الدالة . هو (a † g(x)| |g(x) = (b 1 حدد قيمة x التي تكون الدالة (x) عندها غير معرفة. x + 2 = 0 x=-2 (x) غير معرفة عند 2 = x ، وهذا يعني وجود خط تقارب رأسي عند 2 = x ، وبما أن 1 - = c ، فإنه يوجد خط تقارب أفقي عند 1- = y (لاحظ أنه كلما زادت قيم x الأكبر من - تقترب قيم ) من 1 وكلما قلت قيم x الأقل من 2 تقترب قيم (x) من 1 أيضًا، وهذا يعني وجود خط تقارب أفقي عند 1- = y ) . الأعداد الحقيقية ما عدا -2 . أما المدى فهو جميع الأعداد الحقيقية ما عدا 1 . مجال الدالة . هو جميع تحقق من فهمك وزارة التعليم 4 (x) (33) of (x) A (3) f(x)=-4₂ |g(x)= + الدرس 3-3- تمثيل دوال المقلوب بيانيا 87 2024-1446 -: 0 إرشادات للدراسة خطوط التقارب يبين خط التقارب الرأسي قيمة X التي تكون الدالة عندها غير معرفة. أما خط التقارب الأفقي فيبين سلوك طرفي التمثيل البياني.

الربط بالحياة تأسست الخطوط السعودية في عام 1946م، وكانت أولى رحلاتها الدولية إلى مطار (اللد) في فلسطين لنقل الحجاج. تأكد يمكنك استعمال دوال المقلوب لحل مسائل حياتية عديدة. مثال 4 من واقع الحياة كتابة معادلات دوال المقلوب طيران تقطع طائرة ركاب مسافة 7500 ميل في إحدى الرحلات. اكتب دالة تبين الزمن الذي تحتاج إليه الطائرة لتقطع هذه المسافة بدلالة السرعة r. ومثل هذه الدالة بيانيا. حل المعادلة rt = d بالنسبة للمتغير } . rt = d t = 7500 t= r المعادلة الأصلية اقسم كل من الطرفين على " d = 7500 مثل الدالة 2500 = t بيانيا، عين النقاط : (1500,5) (750,10) (500,15) (250,30) ) وضّح أية قيود يمكن وضعها على كلِّ من المجال والمدى فيه هذه الحالة. th 192 168 144 120- 196 7500 0 500 1000 1500 2000 المجال والمدى في هذه الحالة هما مجموعة جزئية من مجموعة الأعداد الحقيقية الموجبة؛ لأن القيم السالبة في هذه الحالة غير منطقية. وهناك شرط أو قيد إضافي على المجال؛ لأن للطائرة سرعة عظمى، وأخرى صغرى تستطيع الطيران بها. تحقق من فهمك (4) رحلات نظم طلاب الصف الثاني الثانوي في مدرسة أهلية رحلة إلى منطقة أثرية بإشراف إدارة مدرستهم، حيث دفع كل واحد منهم 45 ريالًا ثمناً للوجبات الغذائية وتكفلت إدارة المدرسة بنفقات إضافية للرحلة وهي 2500 ريال. اكتب دالّة تمثل متوسط التكلفة الكلية للطالب الواحد ومثلها بيانيا. ووضّح أية قيود يمكن وضعها على كل من المجال والمدى. مثال 1 1) حدد قيمة x التي تجعل الدالة 4 = (f(x غير معرفة. 4x-8 مثال 2 مثل كل دالة مما يأتي بيانيا، وحدد مجال ومدى كل منها: f(x) (2 f(x) = x3 (3 مثال 3 حدد خطوط التقارب والمجال والمدى لكل من الدالّتين الآتيتين: f(x) (5 -8 -0 f(x) = f(x) 4 f(x)+ D (4 مثال 4 6) هدية جماعية : يرغب بعض الطلاب في إرسال هدية ثمنها 150 ريالًا إلى أحد أصدقائهم. ) فإذا كانت ، تمثل المبلغ الذي يدفعه كل منهم، وأعدد الأصدقاء، فاكتب دالة تمثل المبلغ الذي يدفعه كل منهم بدلالة عدد الأصدقاء. b) مثل هذه الدالة بيانيا. وضح أية قيود يمكن وضعها على كلّ من المجال والمدى في هذه الحالة. وزارة التعليم Ministry of Education 2024-1446 الفصل 5 العلاقات والدوال النسبية 88

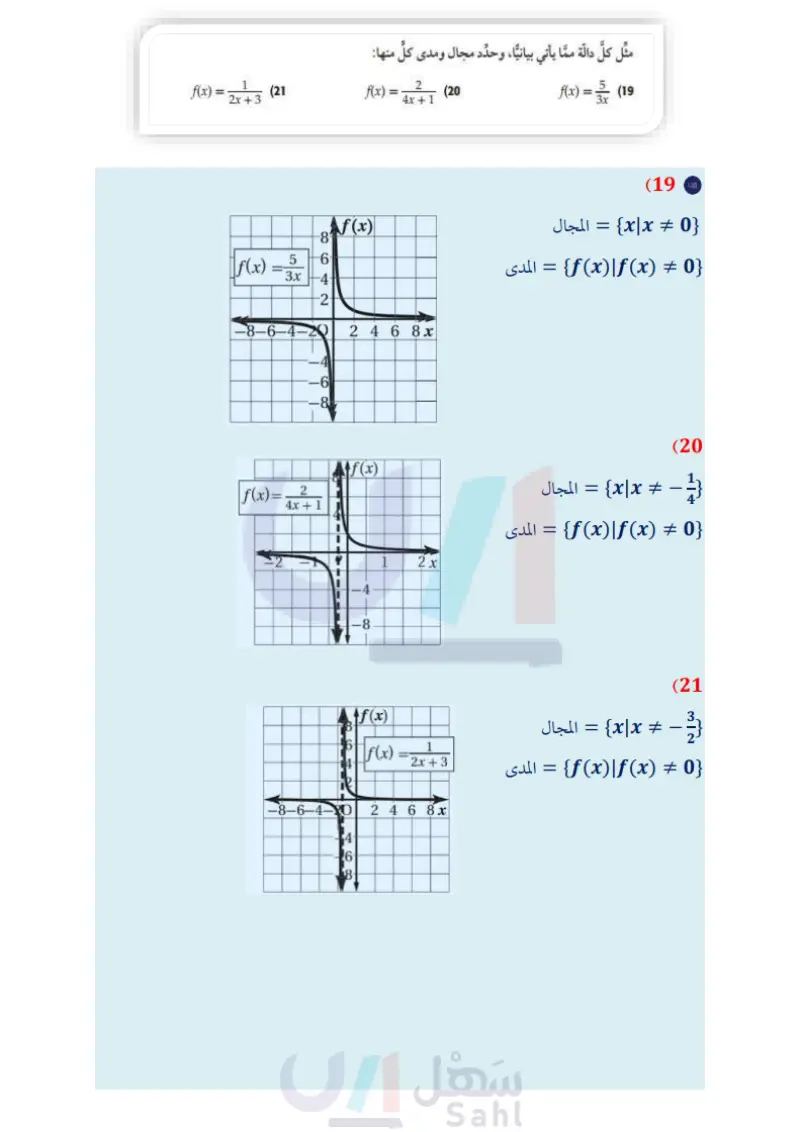
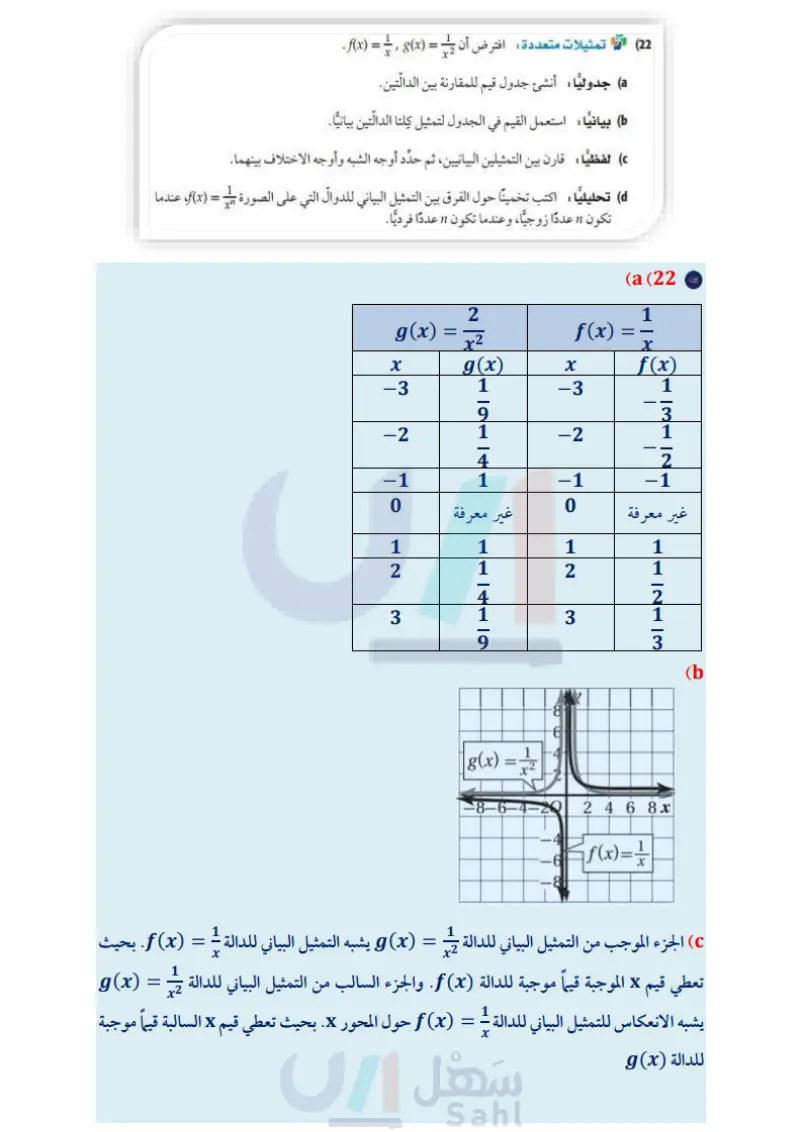
تدرب وحل المسائل مثال 1 حدد قيمة x التي تجعل كل دالة فيما يأتي غير معرفة. f(x) = √(7 f(x) = (9 3x+9 f(x) = x×7 (8 مثال 2 مثل كل دالة مما يأتي بيانيا، وحدد مجال ومدى كلٌّ منها: f(x) = x-6 26 (12 f(x) = x+2 (11 f(x) = x+3 +6 (15 f(x) = x 37 - 8 (14 f(x) 10 f(x) = (10 f(x)= (13 مثال 3 حدد خطوط التقارب والمجال والمدى لكل من الدالّتين الآتيتين: f(x)=3 (17 Aff(x) 4 ° 4 flo (16 مثال 4 18) كيمياء لدى محمد 200 جرام (8) من سائل مجهول. وتساعد معرفة كثافة السائل على تحديد نوعه. ويمكن حساب كثافة السائل بقسمة كتلته على حجمه. a) اكتب دالة تمثل كثافة هذا السائل (d) بدلالة حجمه (7). b) مثل هذه الدالة بيانيا. استعمل التمثيل البياني لتحديد خطوط التقارب والمجال والمدى لهذه الدالة. مثل كلَّ دالة مما يأتي بيانيا، وحدد مجال ومدى كل منها: f(x) = (21 2x + 3 f(x) = 2 4x+1 (20 f(x) = 3x (19 (22) تمثيلات متعددة : افترض أن = (f(x) = { , (x . a) جدوليًا: أنشئ جدول قيم للمقارنة بين الدالّتين. ) بيانيا : استعمل القيم في الجدول لتمثيل كلتا الدالّتين بيانيا. لفظيا : قارن بين التمثيلين البيانيين، ثم حدد أوجه الشبه وأوجه الاختلاف بينهما. تحليليا : اكتب تخمينا حول الفرق بين التمثيل البياني للدوال التي على الصورة = (f(x، عندما تكون n عددًا زوجيا، وعندما تكون n عددًا فرديًا. وزارة التعليم 89 2024-1446 الدرس 3-5 تمثيل دوال المقلوب بيانيا

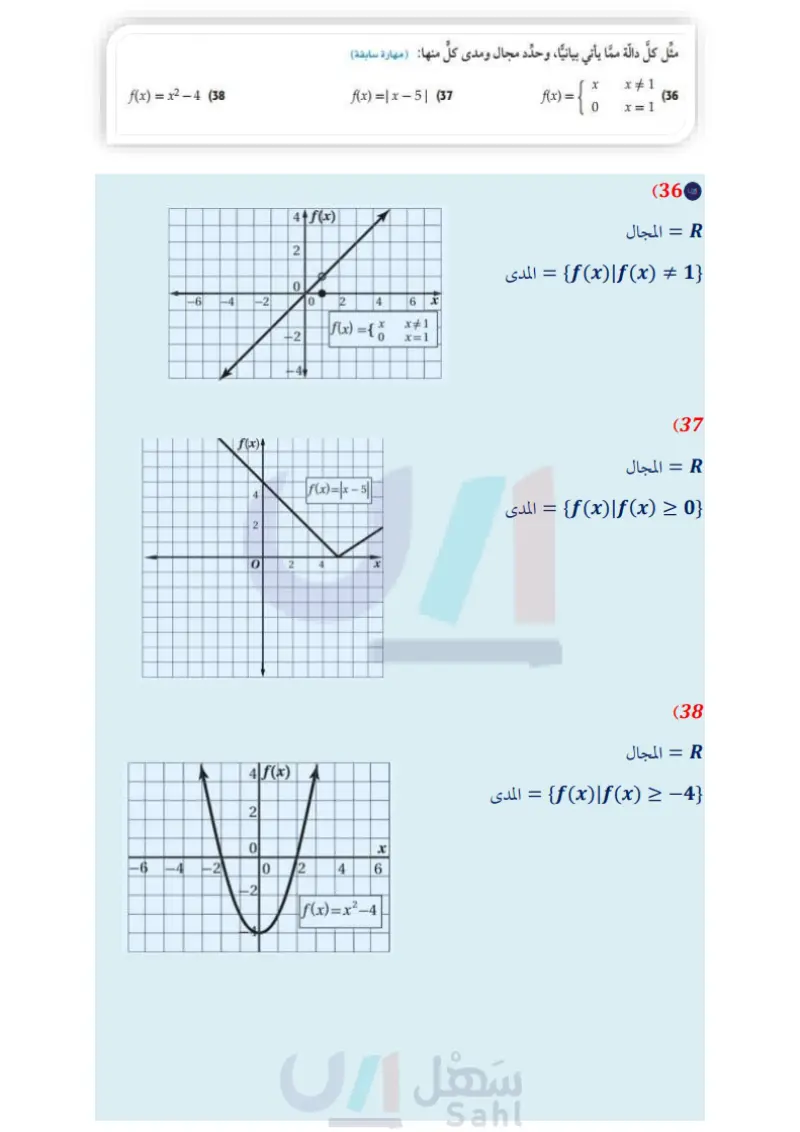
مسائل مهارات التفكير العليا (23) مسألة مفتوحة : اكتب دالّة مقلوب يكون لتمثيلها البياني خط تقارب رأسي عند 4 = x، وخط تقارب أفقي عند 6 = y . (24) تبرير قارن بين التمثيلين البيانيين لكل زوج من المعادلات الآتية موضحا أوجه الشبه وأوجه الاختلاف. y = 1, y-7= (a y= 1,y=4(1) (b y= 1,y=x+5 (c استعمل ملاحظاتك في الفروع c - 2 لتمثيل الدالة - 3 - 4 - . = 7 - y بيانيا دون استعمال جدول قيم. 1x+5 (25) أيها لا ينتمي؟ حدد الدالة المختلفة عن الدوال الثلاث الأخرى، ووضّح إجابتك. j(x) = 20 x-7 5 h(x) = g(x) = x2 + 2x + 1 x+2 x2 + 1 f(x) = x+1 26) تحد: اكتب دالتي مقلوب، يكون للتمثيل البياني لكلِّ منهما خطا التقارب نفساهما، ثم مثل هاتين الدالّتين بيانيا. 27) اكتب: ارجع إلى فقرة "لماذا" في بداية هذا الدرس، ووضّح كيف يمكن استعمال دوال المقلوب عند جمع التبرعات. وبيّن لماذا يكون جزء من التمثيل البياني للدالة فقط منطقيا بالنسبة لسياق الموقف. تدريب على اختبار 28) ما مجال الدالة ح = (f(x؟ x+3 مجموعة الأعداد الحقيقية. مجموعة الأعداد الحقيقية الموجبة. مجموعة الأعداد الحقيقية ما عدا .3 مجموعة الأعداد الحقيقية ما عدا 3 مراجعة تراكمية بسط كل عبارة مما يأتي: (الدرس 1-5) (29) ما قيمة العبارة (y) (y)، إذا كانت 10 = xy = - 3, x2 + y2؟ 4 A 7B 13 C 16 D وزارة التعليم Ministry of Education 2024-1446 x+y 2x-y x+y 2x + y (32 m + g 5 m² +92 5 (31 (30 أوجد () () () () () (8) ,(x) (+) للدالتين (f(x), (x في كل مما يأتي: (مهارة سابقة) f(x) = 2x² (35 g(x)=8-x f(x)=2x-3 (34 g(x)=4x+9 f(x) = x+9 (33 g(x)=x-9 مثل كلَّ دالة مما يأتي بيانيًا، وحدد مجال ومدى كل منها: (مهارة سابقة) f(x) = x2 - 4 (38) f(x) = | x - 5 | (37) f(x) = { x#1 x (36 0 x=1 الفصل 5 العلاقات والدوال النسبية 90

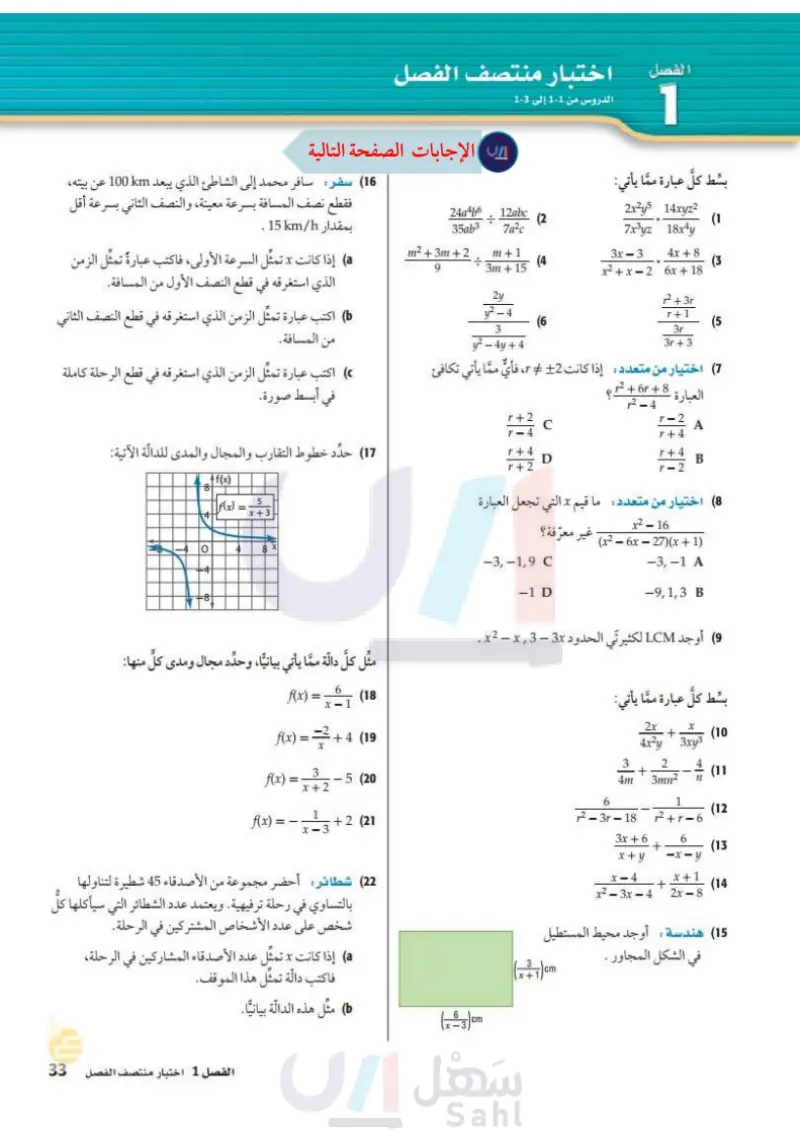
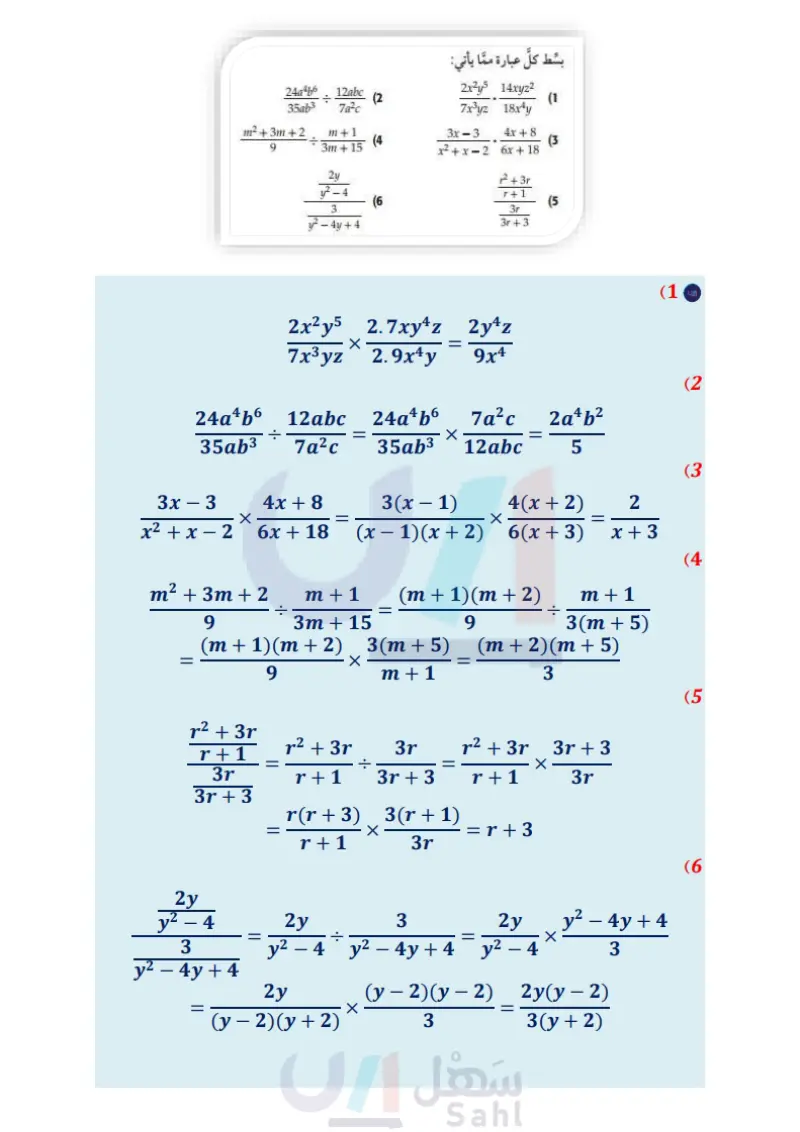
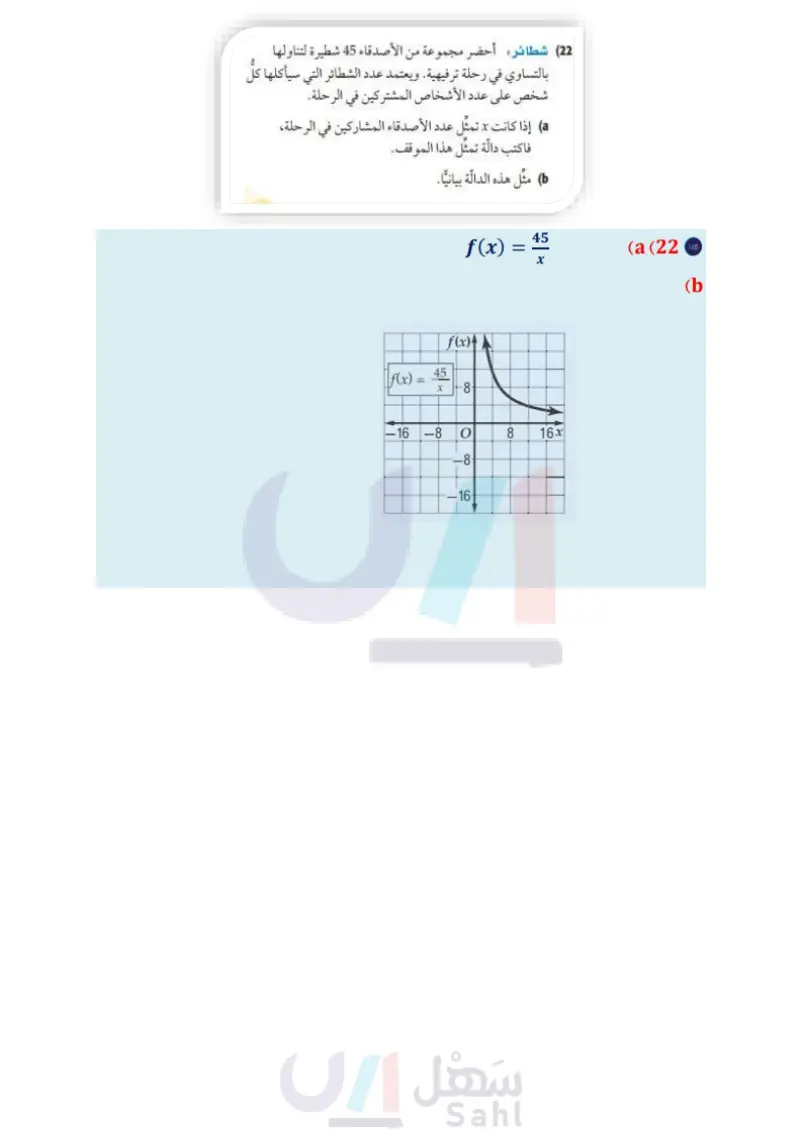
الفصل 5 اختبار منتصف الفصل الدروس من 1 إلى 3-5 بسط كل عبارة مما يأتي: 24a4b6 35ab3 12abc 2x²y5 14xyz2 (2 (1 7a²c 7x³yz 18x4y m2 + 3m + 2 9 m+1 (4) 3m + 15 3x-3 x 2 + x - 2 4x+8 (3 6x + 18 21/ 2 + 3r y²-4 r+1 (6 (5 3 3r 3r+3 y²-4y+4 (7) اختيار من متعدد : إذا كانت 2 r، فأي مما يأتي تكافئ العبارة r²+6r+8 2-4 A r+4 r+4 B 1-2 r+2 1+4 r+2 D 8 اختيار من متعدد ما قيم x التي تجعل العبارة (16) سفر: سافر محمد إلى الشاطئ الذي يبعد km 100 عن بيته، فقطع نصف المسافة بسرعة معينة، والنصف الثاني بسرعة أقل بمقدار km/h 15 . a إذا كانت x تمثل السرعة الأولى، فاكتب عبارة تمثل الزمن الذي استغرقه في قطع النصف الأول من المسافة. ) اكتب عبارة تمثل الزمن الذي استغرقه في قطع النصف الثاني من المسافة. اكتب عبارة تمثل الزمن الذي استغرقه في قطع الرحلة كاملة في أبسط صورة. (17) حدد خطوط التقارب والمجال والمدى للدالة الآتية: f(x) T |f(x) = له 2 - 16 (x²-6x-27)(x+1) -3,-1 A -9,1,3 B غير معرفة؟ -3,-1,9 C -1 D -4 10 8x 9) أوجد LCM لكثيرتي الحدود x2 - x - 3x . بسط كل عبارة مما يأتي: مثل كلَّ دالة مما يأتي بيانيا، وحدد مجال ومدى كلّ منها: f(x)= )=x-1 (18 f(x) = 2 + 4 (19 2x 4x²y (10 3xy 3 2 + f(x)= 5 (20 4m n 3mn² (11 x+2 6 1 (12) f(x)=- x 3 +2 (21 2 - 3 - 18 2 - 1 - 6 3x + 6 6 + (13 x+y x-4 -x-y + x - 3x - 4 x+1 2x-8 (14 15) هندسة أوجد محيط المستطيل في الشكل المجاور . (22) شطائر: أحضر مجموعة من الأصدقاء 45 شطيرة لتناولها بالتساوي في رحلة ترفيهية. ويعتمد عدد الشطائر التي سيأكلها كلُّ شخص على عدد الأشخاص المشتركين في الرحلة. a إذا كانت x تمثل عدد الأصدقاء المشاركين في الرحلة، فاكتب دالّة تمثل هذا الموقف. (x-3)cm مثل هذه الدالة بيانيا. وزارة التعليم الفصل 5 اختبار منتصف الفصل 91 2024-1446