الجذر النوني - رياضيات2-2 - ثاني ثانوي

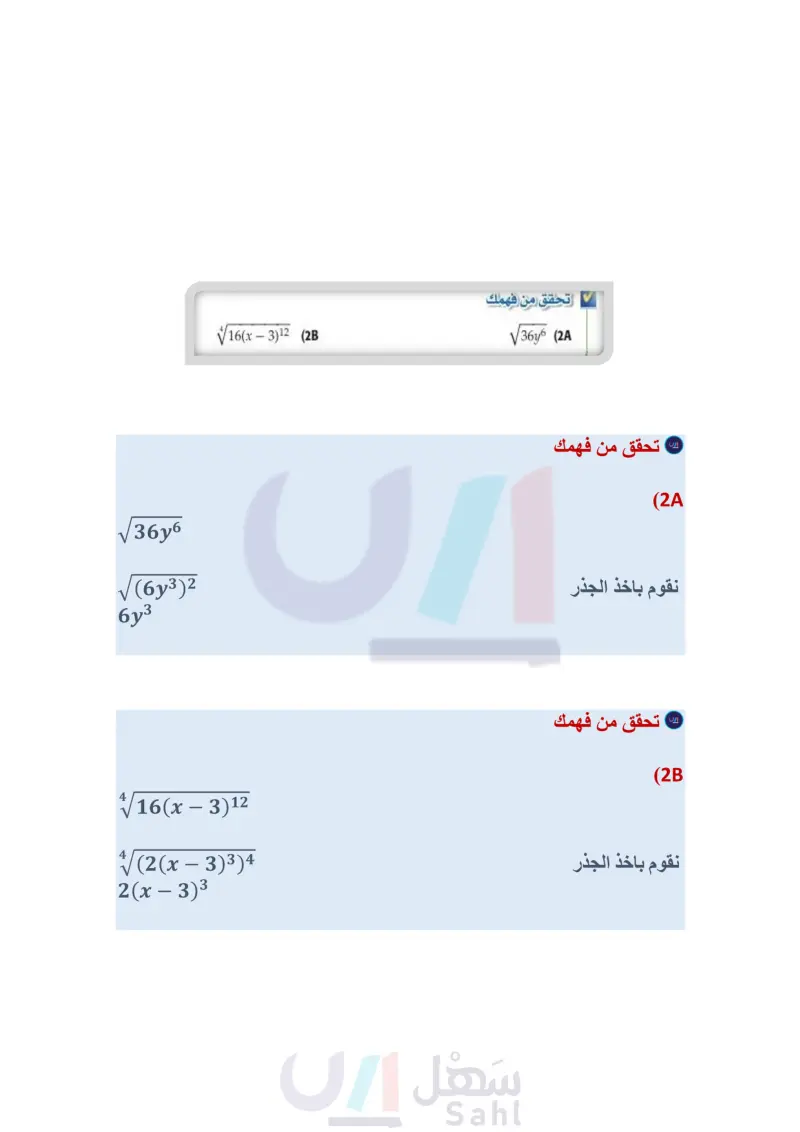
أضف إلى مطويتك الجذر النوني الحقيقي مفهوم أساسي لیکن n عددًا صحيحًا أكبر من 1 ، و 1 عددًا حقيقيًّا. a n عدد زوجي n عدد فردي هناك جذر حقيقي موجب وحيد، وجذر حقيقي سالب هناك جذر حقيقي موجب وحيد وليس وحيد ، الجذر الموجب هو الجذر الرئيس هناك جذر حقيقي سالب Va. ليس هناك جذور حقيقية موجبة وهناك ليس هناك جذور حقيقية فقط جذر حقيقي سالب وحيد Va هناك فقط جذر حقيقي 0 = 0 - 6)8 (b -V[(x2 – 6)? - V2 - 68 = - =-(x²- 6)4 معكوس الجذر التربيعي الرئيس لـ -(x² -6)4(x² - 6)8 √128 (d √128 = √27 =2 الجذر السابع لـ 128 هو 2 -√√(y+7)16 (1B .3a4b5 a > 0 a<0 a=0 مثال 1 إيجاد الجذور بسط كلًا مما يأتي: ±√√16y (a ±√16y= ±√√(4y²)2 = +4y² الجذران التربيعيان لـ 164 هما 1412 . √√243a201,25 (c √243a20b25 = √(3a4b5)5 = 3a4b5 الجذر الخامس لـ 243a20b25 هو تحقق من فهمك 86 1 إرشادات للدراسة . دليل الجذر إذا كان n عددًا فرديا إذا كان دليل الجذر عددًا زوجيًا وأس ما تحت الجذر عددًا ،زوجيًّا، وكان أس الناتج عددًا فرديًا، يجب أن تجد القيمة المطلقة للناتج لتتأكد من أن الجواب ليس سالبًا. مثال 2 التبسيط باستعمال القيمة المطلقة بسط كلًا مما يأتي: √64(x²-3)18 (b √64(x2-3) 18 = 2 (x² - 3)³ | بما أن دليل الجذر (العدد 6) عدد زوجي، وأس √y (a V= = |y| بما أن لا من الممكن أن تكون سالبة فالجذر الرئيس لهذه العبارة يساوي القيمة المطلقة لها. العبارة 3 - x2 العدد (3) عدد فردي فيجب استعمال رمز القيمة المطلقة. وزارة التعليم الدرس 4-4 الجذر النوني 31 2024-1446 16(x-3)12 (2B تحقق من فهمك √36y6 (2A فهناك فقط جذر حقيقي واحد، وبناءً على ذلك، فلا يوجد هناك جذر رئيس ولا يوجد حاجة إلى استعمال رمز القيمة المطلقة. أما إذا كان n عددًا زوجيا فإن √√x" =|x|

الربط مع الحياة تشير الإحصاءات في الولايات المتحدة إلى وقوع أكثر من 500 ألف حادث اصطدام للدراجات الهوائية والسقوط من عليها وإصابة راكبيها سنويًا، منهم أكثر من 11 ألف طفل ومراهق مما يرفع تكلفة العلاج إلى ما يجاوز 200 مليون دولار سنويًا. ويُنصح بارتداء الخوذة لأهميتها لحماية رؤوس راكبي الدراجات الهوائية عند تعرضهم لحوادث السقوط. تقريب الجذور باستعمال الحاسبة تذكَّر أن الأعداد الحقيقية التي لا يمكن كتابتها في صورة كسور عشرية منتهية أو دورية، تُسمى أعدادًا غير نسبية. وغالبًا ما يستعمل تقريب الأعداد غير النسبية في مسائل من واقع الحياة. مثال 3 من واقع الحياة تقريب الجذور حوادث الدراجات ارجع إلى الفقرة الواردة في بداية الدرس. a إذا كانت c = b2 تمثل عدد الحوادث، وما تمثل عدد الدراجات الهوائية، فقدر عدد الحوادث الشهرية على طريق ما إذا علم أن 1000 دراجة تمر خلاله كل شهر. افهم المعطيات: 102 c = توضح العلاقة بين عدد الدراجات الهوائية (b) التي تمر في طريق، وعدد الحوادث (c) بينها وبين السيارات . عدد الدراجات الهوائية التي تمر خلال الطريق كل شهر هو 1000 دراجة. المطلوب: تقدير عدد الحوادث بين الدراجات الهوائية والسيارات في هذا الطريق خلال شهر. خط عوض عن 6 عدد الدراجات الهوائية) بالعدد 1000. حل تحقق c = √√b² V10002 15.85 المعادلة الأصلية b = 1000 باستعمال الحاسبة فهناك 16 حادثاً تقريبًا كل شهر على ذلك الطريق. 15.85 2 2 15.85562 1000337b2 / 1000 = b c = 15.85 ارفع الطرفين للأس 5 بسط 32 خُذ الجذر التربيعي للطرفين، مع إهمال الجذر السالب إذا كان عدد الحوادث المسجلة على طريق ما في أحد الأشهر يساوي 21 حادثا، فقدر عدد الدراجات الهوائية التي مرت في الطريق خلال ذلك الشهر. المعادلة الأصلية C= 2 c=21 ارفع الطرفين للأس 5 بسط 21 = 2 215 = 62 4084101b2 2021 = b خذ الجذر التربيعي للطرفين، مع إهمال الجذر السالب إذن عدد الدراجات الهوائية التي مرَّت في الطريق خلال ذلك الشهر هو 2021 دراجةً تقريبًا. تحقق من فهمك 3A قياس يمكن إيجاد مساحة سطح كرة إذا علم حجمها، باستعمال الدالة S = V367V2، حيث V تمثل حجم الكرة. أوجد مساحة سطح كرة حجمها 200in3 . 3 قياس : إذا كانت مساحة سطح كرة تساوي 214.5in2، فأوجد حجم الكرة. تأكد المثالان 12 بسط كلا مما يأتي: -√494812 (2 √16816124 (4 √√64(2y+1)18 (6 ±√100y³ (1 VU - -6)8 (3 -125 (5 الفصل 4 العلاقات والدوال العكسية والجذرية وزارة التعليم Ministry of Education 2024-1446

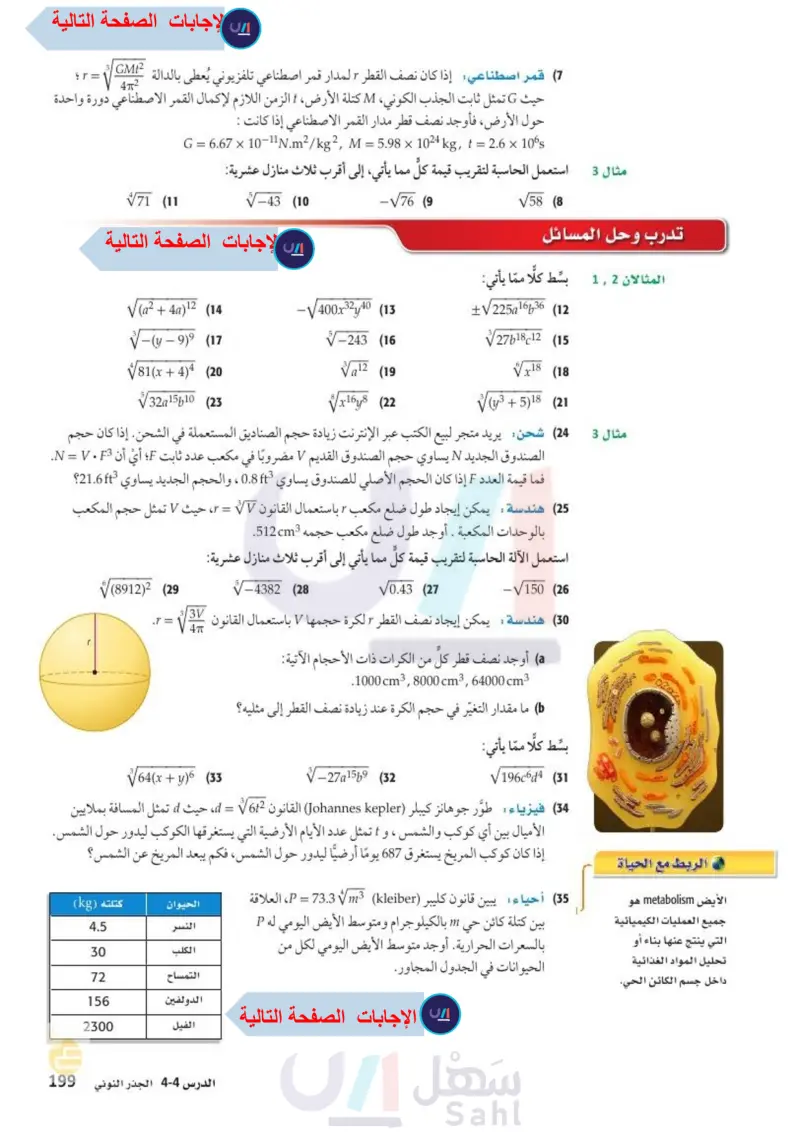
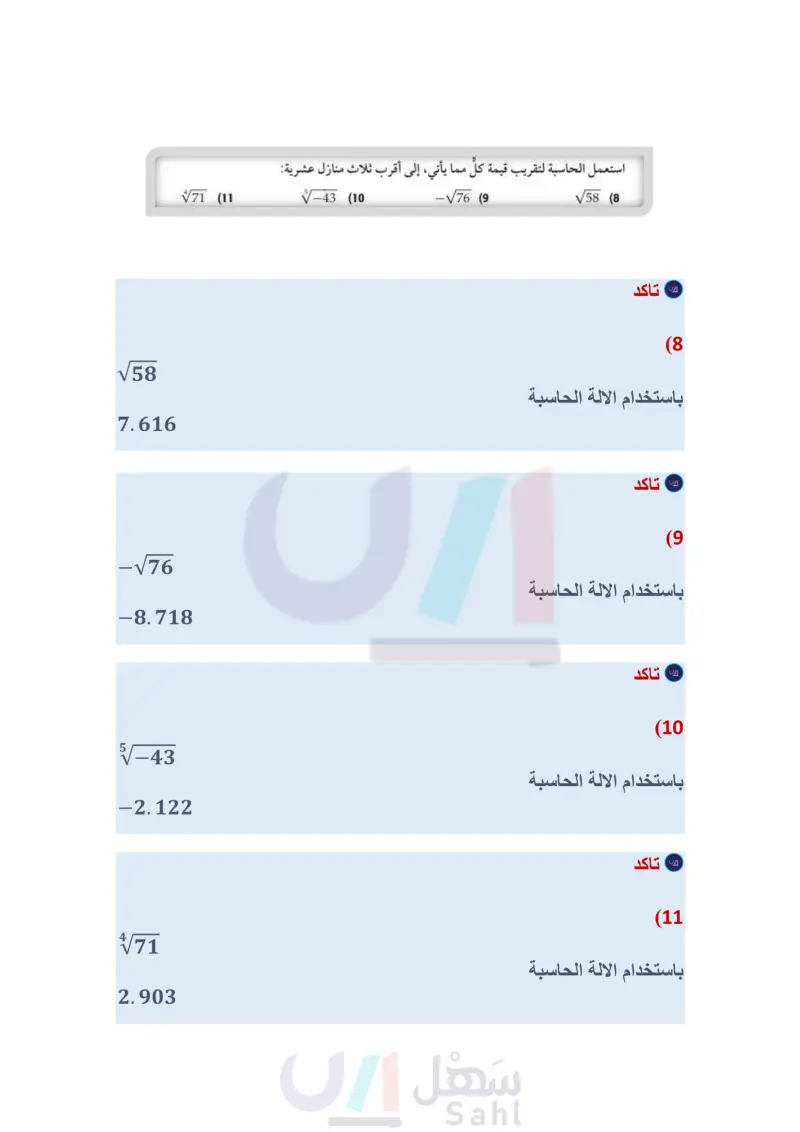
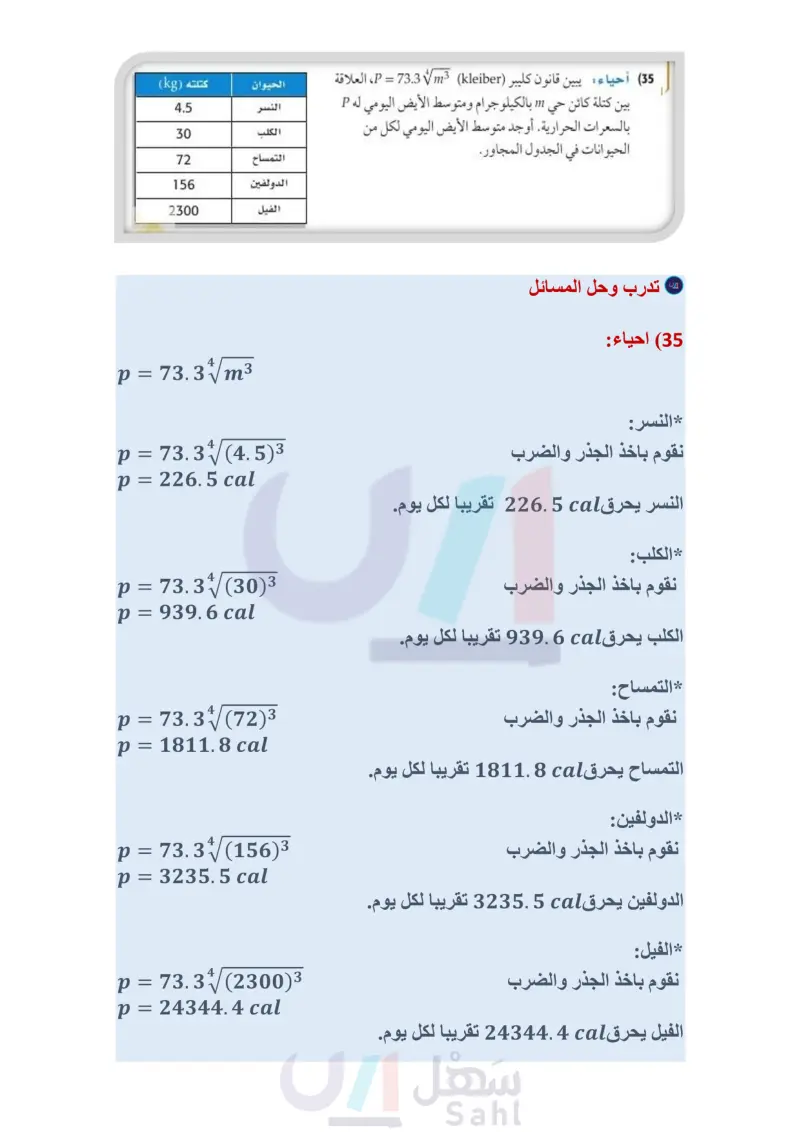
= GMt2 472 (7) قمر اصطناعي: إذا كان نصف القطر r لمدار قمر اصطناعي تلفزيوني يُعطى بالدالة حيث G تمثل ثابت الجذب الكوني، كتلة الأرض، الزمن اللازم لإكمال القمر الاصطناعي دورة واحدة حول الأرض، فأوجد نصف قطر مدار القمر الاصطناعي إذا كانت : G = 6.67 × 10-11N.m2/kg2, M = 5.98 × 1024 kg, t = 2.6 × 106s مثال 3 استعمل الحاسبة لتقريب قيمة كل مما يأتي، إلى أقرب ثلاث منازل عشرية: √58 (8 تدرب وحل المسائل المثالان 12 بسط كلًا مما يأتي: -√√76 (9 -43 (10 √71 (11 √(a²+4a)12 (14 -√400x3240 (13 -(y-9)9 (17 -243 (16 √√81(x+4)4 (20 a12 (19 √32a15610 (23 √x16y8 (22 ±√225a16636 (12 2761812 (15 18 (18 (y3+5)18 (21 مثال 3 24) شحن يريد متجر لبيع الكتب عبر الإنترنت زيادة حجم الصناديق المستعملة في الشحن. إذا كان حجم الصندوق الجديد N يساوي حجم الصندوق القديم V مضروبا في مكعب عدد ثابت F؛ أي أن N = V. F3. فما قيمة العدد F إذا كان الحجم الأصلي للصندوق يساوي 0.8f8 ، والحجم الجديد يساوي 21.6f3؟ V ، حيث V تمثل حجم المكعب (25) هندسة: يمكن إيجاد طول ضلع مكعب " باستعمال القانون r = بالوحدات المكعبة . أوجد طول ضلع مكعب حجمه 512cm3. استعمل الآلة الحاسبة لتقريب قيمة كل مما يأتي إلى أقرب ثلاث منازل عشرية: -√150 (26 √0.43 (27 -4382 (28 30) هندسة : يمكن إيجاد نصف القطر " لكرة حجمها V باستعمال القانون : a) أوجد نصف قطر كل من الكرات ذات الأحجام الآتية: .1000cm3, 8000 cm3, 64000 cm3 ) ما مقدار التغير في حجم الكرة عند زيادة نصف القطر إلى مثليه؟ (8912)2 (29 .r= √√64(x+y)6 (33 -27a15b9 (32 بسط كلًا مما يأتي: √196c6d4 (31 في الربط مع الحياة الأيض metabolism . هو جميع العمليات الكيميائية التي ينتج عنها بناء أو تحليل المواد الغذائية داخل جسم الكائن الحي. 34 فيزياء طور جوهانز كيبلر (Johannes Kepler القانون 62 = d، حيث d تمثل المسافة بملايين الأميال بين أي كوكب والشمس ، و ا تمثل عدد الأيام الأرضية التي يستغرقها الكوكب ليدور حول الشمس. إذا كان كوكب المريخ يستغرق 687 يومًا أرضيا ليدور حول الشمس، فكم يبعد المريخ عن الشمس؟ (35) أحياء يبين قانون کلیبر (P = 73.33 (Kleiber، العلاقة الحيوان بين كتلة كائن حي " بالكيلو جرام ومتوسط الأيض اليومي له P بالسعرات الحرارية. أوجد متوسط الأيض اليومي لكل من الحيوانات في الجدول المجاور. النسر الكلب التمساح الدولفين الفيل كتلته (kg) 4.5 30 72 156 2300 وزارة التعليم الدرس 4-4 الجذر النوني 33 2024-1446

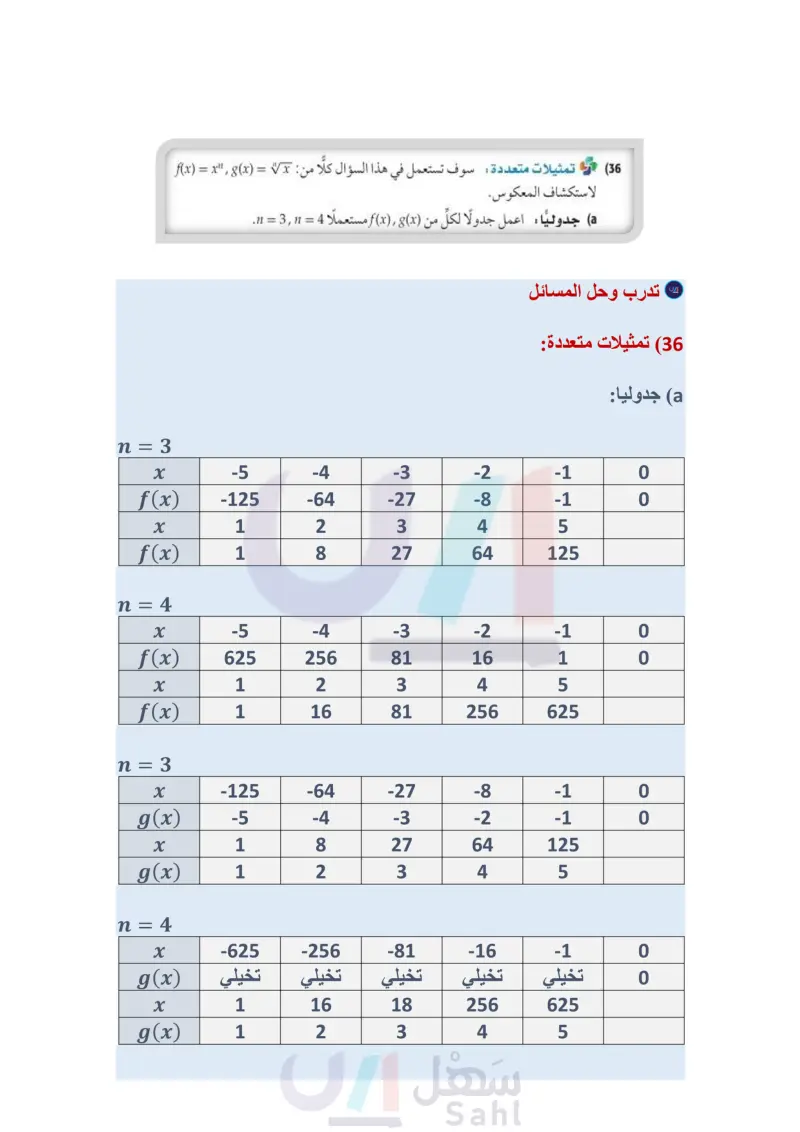
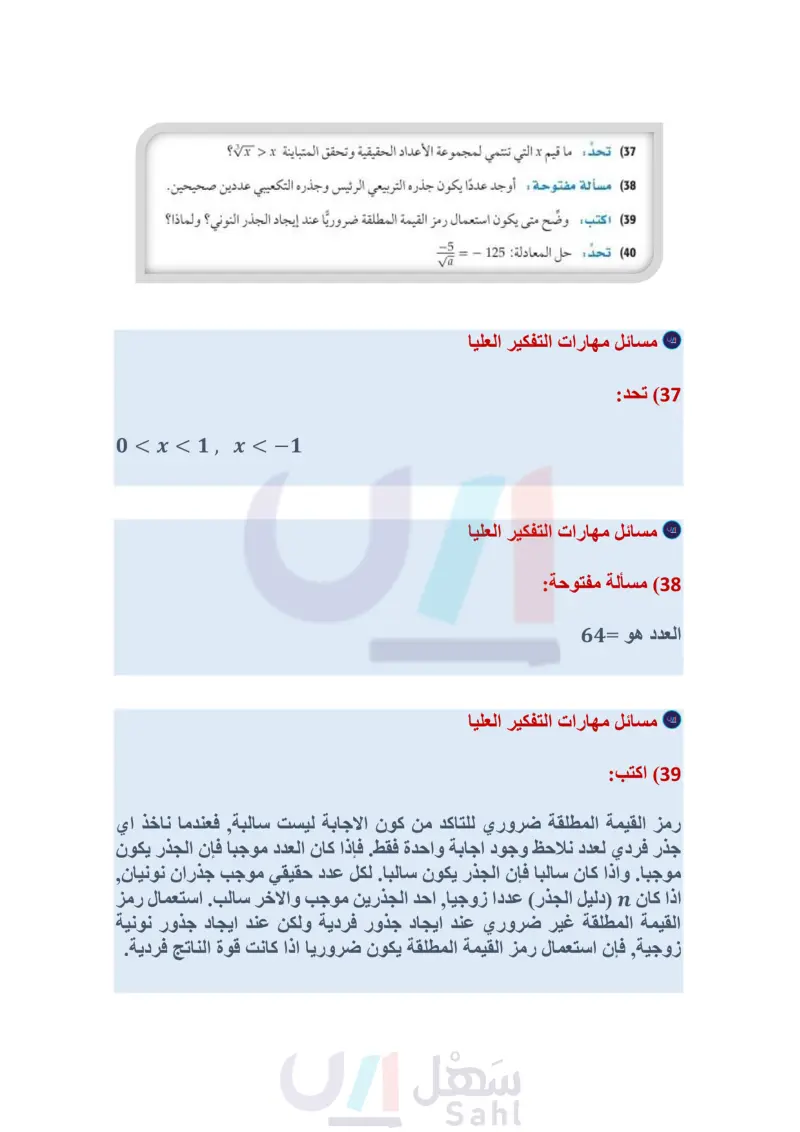
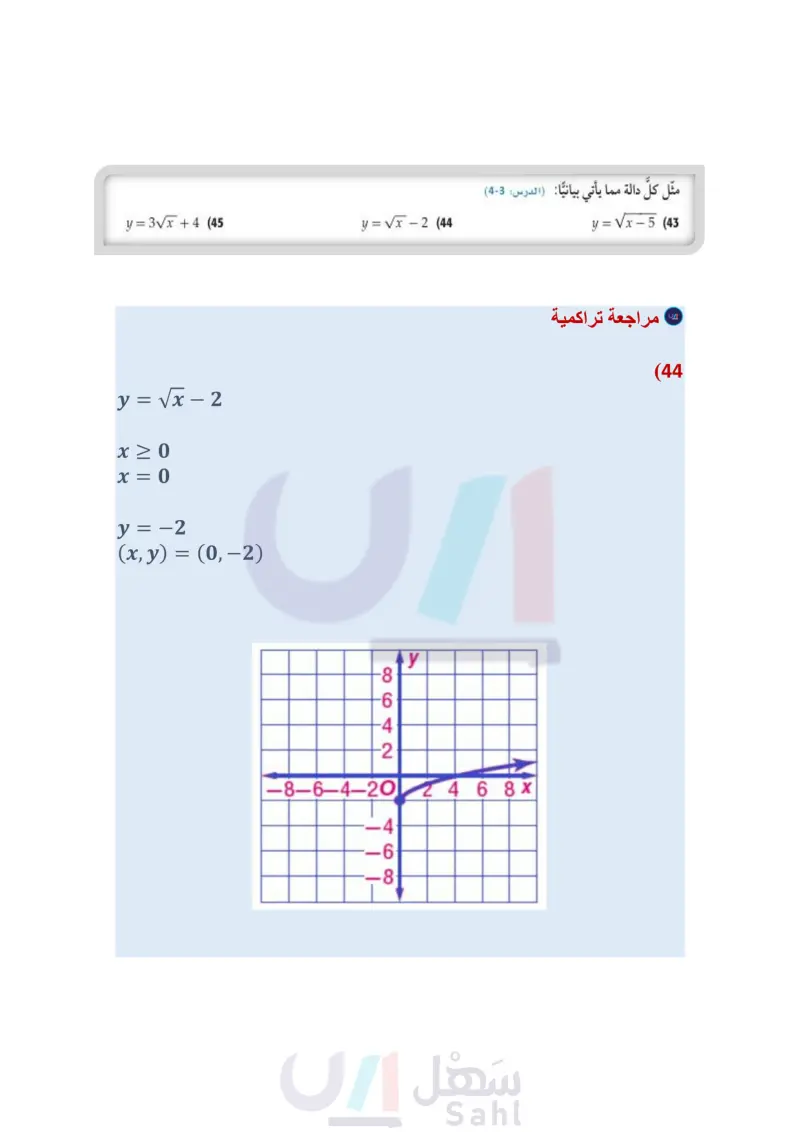
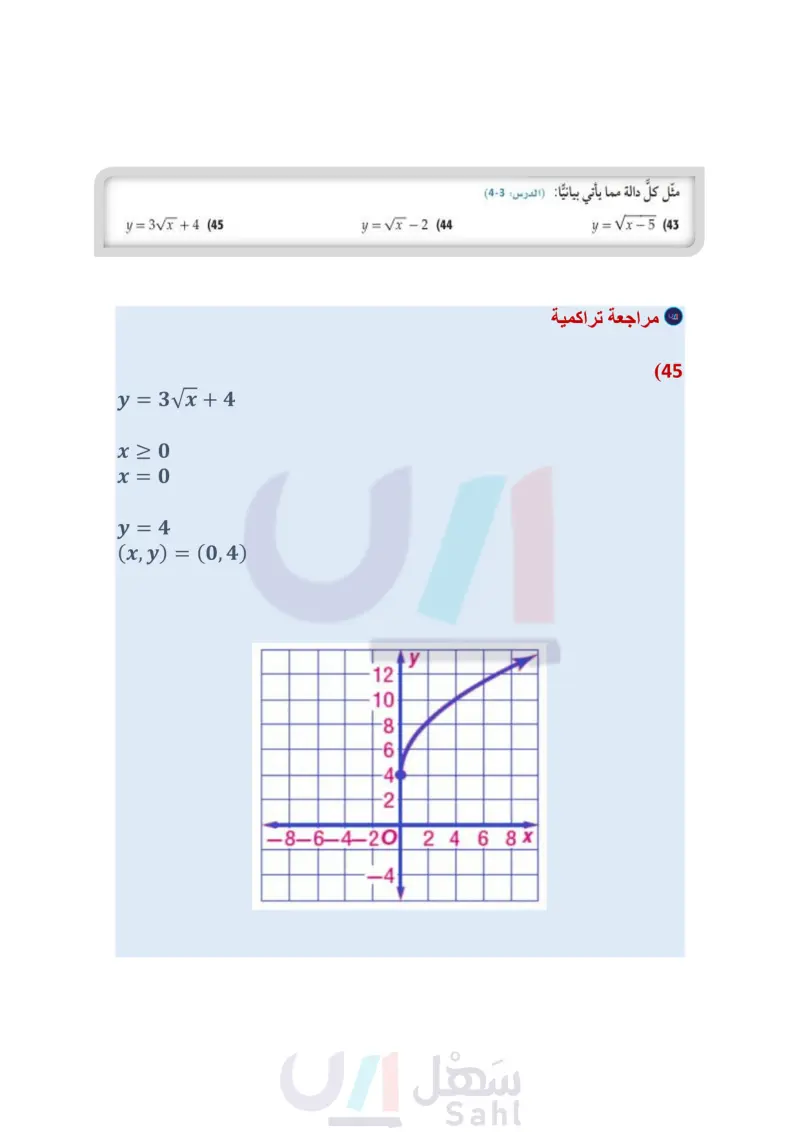
(36) و تمثيلات متعددة سوف تستعمل في هذا السؤال كلا من: f(x) = x ,(x) = T لاستكشاف المعكوس. a) جدوليًا : اعمل جدولاً لكل من (f(x) (x مستعملا 4 = n = 3, n . بيانيا : مثل كلا من المعادلتين السابقتين بيانيا. تحليليا أيُّ المعادلتين السابقتين تمثل دالة؟ وأيها تمثل دالة متباينة؟ d تحليليا : ما قيم " التي يكون عندها كلُّ من الدالتين (g(x), f(x دالة عكسية للأخرى؟ e) لفظيا : ما الاستنتاجات التي يمكن أن تتوصل إليها حول x) = x) و "f(x) = x ، لقيم " الزوجية الموجبة، وقيم " الفردية الموجبة؟ مسائل مهارات التفكير العليا (37) تحد ما قيم x التي تنتمي لمجموعة الأعداد الحقيقية وتحقق المتباينة x > x؟ 38 مسألة مفتوحة أوجد عددًا يكون جذره التربيعي الرئيس وجذره التكعيبي عددين صحيحين. 39) اكتب وضّح متى يكون استعمال رمز القيمة المطلقة ضروريًا عند إيجاد الجذر النوني؟ ولماذا؟ (40) تحد حل المعادلة 125 - = : تدريب على اختبار (41) أي الآتية هو الأقرب إلى قيمة المقدار 7.32؟ 42) قيمة 256x816 هي : 16x8 y 16 A 16x2 y16 B 4x² y4 C 4x+y+ D 1.8 A 1.9 B 20 2.1 D مراجعة تراكمية مثل كل دالة م دالة مما يأتي بيانيا : (الدرس: 3-4) y=√x-5 (43 y = V - 2 (44) y = 3VT + 4 (45) (46) صحة تبلغ كتلة طفل وُلد حديثًا 73 أرطال، وطوله 19.5in. فإذا كان الكيلو جرام الواحد يساوي 2.2 رطل تقريبًا، والسنتمتر الواحد يساوي 0.3937in تقريبًا. فأوجد كتلة المولود بالكيلوجرامات وطوله بالسنتمترات. (الدرس (2-4) وزارة التعليم Ministry of Education 2024-1446 2(w+z)(w4z) (51 (2a2+6)2 (48 بسط كلًّا مما يأتي: (مهارة سابقة) (11x²+13x15) (7x29x+19) (47 أوجد حاصل الضرب في كل مما يأتي: (مهارة سابقة) (x+2y)(xy) (50 (x+4)(x+5) (49 الفصل 4 العلاقات والدوال العكسية والجذرية 34