تمثيل الدوال النسبية بيانيا - رياضيات2-2 - ثاني ثانوي

www.icn.cdu.sa تمثيل الدوال النسبية بيانيا Graphing Rational Functions الماذا؟ 5-4 فيما سبق درست تمثيل دوال المقلوب اشترى أحمد آلة تصوير رقمية وطابعة لطباعة الصور بمبلغ إجمالي مقداره 1350 ريالا، وكانت تكلفة الحبر وورق بيانيا. الدرس (3-5) وانان الطباعة للصورة الواحدة 1.5 ريال يمكنه استعمال الدالّة النسبية . . أمثل بيانيا دوال نسبية 1.5p + 1350 C(p)=- P لها خطوط تقارب رأسية لحساب تكلفة طباعة p من الصور وأفقية. . أمثل بيانيا دوال نسبية لها نقاط انفصال. المفردات: الدالة النسبية rational function نقطة الانفصال point discontinuity إرشادات للدراسة مجال الدالة النسبية مجال الدالة النسبية a(x) b(x) = (f(x هي: جميع الأعداد الحقيقية باستثناء تلك الأعداد التي تجعل المقام صفرا a(x) b(x) خطوط التقارب الرأسية والأفقية : الدالّة النسبية . هيد دالة على الصورة - (x)، حيث (x) و (x) كثير تا حدود و 0 (x) . لتمثيل الدالة النسبية بيانيا يكون من المفيد تحديد أصفارها، وخطوط التقارب لها . فأصفار الدالة الا هي جميع قيم x التي يكون عندها 0 = (a(x . مفهوم أساسي a(x) خطوط التقارب الرأسية والأفقية التعبير اللفظي : إذا كان (bx (f(x حيث (x (x كثيرا حدود لا يوجد بينهما عوامل مشتركة غير الواحد، و 0 (x) فإنه : . يوجد للدالة (f(x خط تقارب رأسي عندما 0 = x . . يوجد للدالة (f(x خط تقارب أفقي واحد على الأكثر. . إذا كانت درجة (ax أكبر من درجة (x) فلا يوجد خط تقارب أفقي. b(x) . إذا كانت درجة (x) أقل من درجة (x)، فإن خط التقارب الأفقي هو المستقيم 0 = y. . إذا كانت درجة (x) تساوي درجة (x)، فإن خط التقارب الأفقي هو المستقيم المعامل الرئيس لـ (a(x المعامل الرئيس لـ (x) أمثلة : لا يوجد خط تقارب أفقي .y = يوجد خط تقارب أفقي واحد f(x)= أضف إلى مطويتك f(x) 2x وزارة التعليم Ministry of Education 2024-1446 +F(X) 3x if(x) 10 x 10 f(x) = خطا التقارب الرأسي خط التقارب الرأسي x = 3 x = -1, x = 1 خط التقارب الأفقي خط التقارب الأفقي y=2 y=0 خط التقارب الرأسي x = -1 الفصل 5 العلاقات والدوال النسبية 92

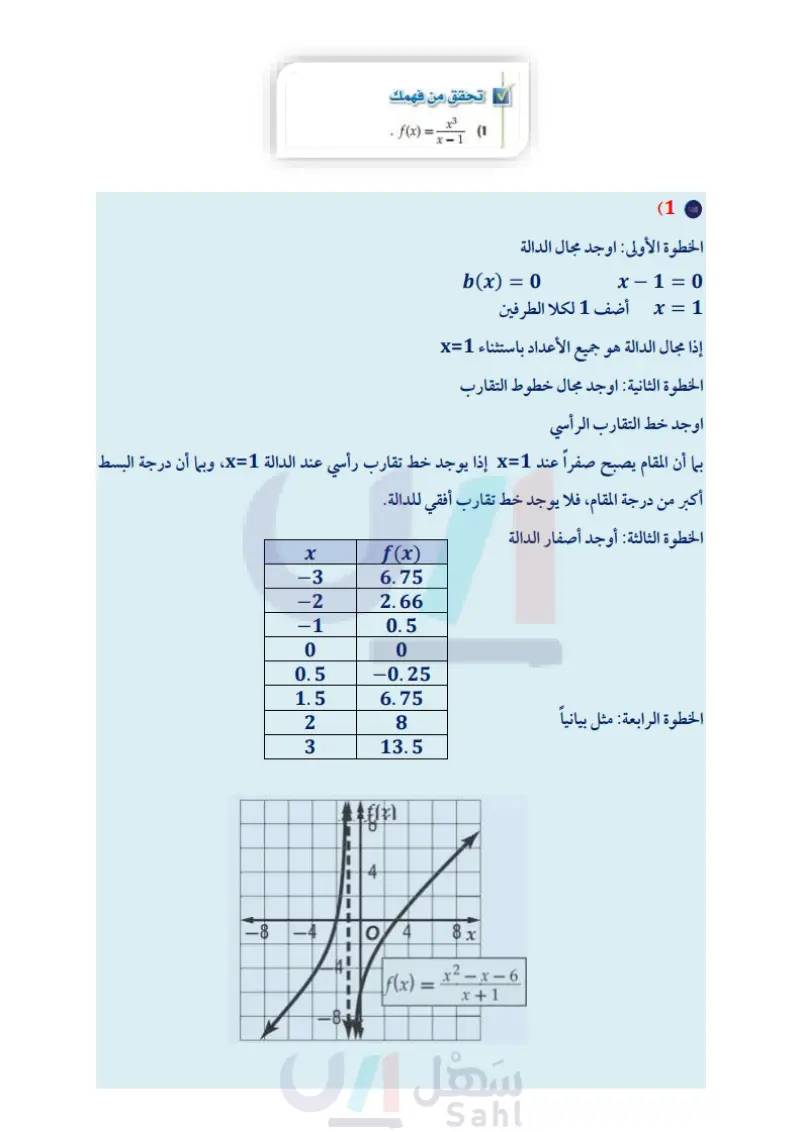
يمكنك استعمال خطوط التقارب لتسهيل تمثيل الدالة النسبية بيانيا، كما يمكنك استعمالها لتوضيح عدد الأجزاء التي ينقسم إليها التمثيل البياني للدالة، فإذا كان هناك خط تقارب رأسي واحد، فإن التمثيل ينقسم إلى فرعين، أما إذا كان هناك خطا تقارب فإنه ينقسم إلى ثلاثة أفرع. مثال 1 التمثيل البياني لدالة نسبية ليس لها خط تقارب أفقي مثل الدالة = (f(x بيانيا . الخطوة 1: أوجد مجال الدالة. x - 1 = 0 x = 1 b(x)=0 أضف 1 لكلا الطرفين إذن مجال الدالة هو جميع ا الأعداد باستثناء 1 = x . الخطوة 2 : أوجد خطوط التقارب. أوجد خط التقارب الرأسي. بما أن المقام يصبح صفرًا عند 1 = x . إذن يوجد خط تقارب رأسي للدالة عند 1 = x . وبما أن درجة البسط أكبر من درجة المقام، فلا يوجد خط تقارب أفقي للدالة. إرشادات للدراسة الخطوة 3 أوجد أصفار الدالة. الحاسبة البيانية يمكنك استعمال تطبيق القوائم وجداول البيانات في الحاسبة البيانية لإنشاء جدول قيم للدالة عندما تكون القيم في الصورة العشرية. x2 = 0 x=0 a(x)=0 خذ الجذر التربيعي لكلا الطرفين يوجد للدالة صفر عندما 0 = x ، وهذا يعني أن منحنى الدالّة يقطع المحور x عند النقطة (0,0). الخطوة 4: مثل بيانيا. أنشئ جدول قيم للدالة لتجد أزواجًا مرتبة تقع على التمثيل البياني، وصل بين تلك النقاط على المستوى الإحداثي. تحقق من فهمك ⋅ f(x)= x f(x) -3 -2.25 -2 -1.33 -1 -0.5 6 8 x 0 0 0.5 -0.5 1.5 4.5 2 4 3 4.5 f(x); وزارة التعليم الدرس 4-5 تمثيل الدوال النسبية بيانيا 93 2024-1446

مثال 2 من واقع الحياة استعمال التمثيل البياني للدوال النسبية الربط بالحياة تقوم قوات خفر السواحل بعمليات المراقبة والحراسة الحدودية والإنقاذ وتقديم المساعدة لمستخدمي المياه الإقليمية في المملكة. متوسط السرعة يسير قارب خفر سواحل عكس اتجاه الموج بسرعة مقدارها r, mi/h. وخلال عودته إلى نقطة الانطلاق سار القارب في اتجاه الموج بسرعة مقدارها mi /h .12 . ويُعطى مقدار متوسط سرعة القارب خلال رحلة الذهاب والعودة بالصيغة 21112 11+12 . R =- a) إذا كان 1 هو المتغير المستقل، و R هو المتغير التابع فمثل الصيغة بيانيًا عندما mi /h 10 = 12 . بتعويض قيمة 12 تصبح الدالة 20r₁ 1 + 10 . R = 2r₁(10) 1 + (10) = ويكون خط التقارب الرأسي هو 10- = 11 . وخط التقارب الأفقي هو 20 = R مثل خطَّي التقارب والدالة بيانيا. ما مقطع المحور R للتمثيل البياني ؟ مقطع المحور R هو 0 = R . ما قيم المجال والمدى المنطقية في سياق المسألة؟ R 480 40 -40 -20 YO 20 40 في سياق المسألة، مقدار السرعة غير سالب؛ لذا فإن قيم 11 الأكبر من أو التي تساوي الصفر هيا تكون واقعية منطقية، وقيم R المنطقية هي بين 0 و 20 . تحقق من فهمك x + 1 التي (2) رواتب تستعمل إحدى الشركات الدالة 250 + x 13500 . = x لحساب راتب موظف خلال السنة x من . عمله لديها، مثل هذه الدالة بيانيًا. وحدد القيم المنطقية لمجال الدالّة ومداها في سياق المسألة، وعلى ماذا يدل خط التقارب الأفقي في هذه المسألة؟ نقطة الانفصال يوجد في بعض الأحيان نقط انفصال في التمثيل البياني للدالة النسبية، وتظهر هذه النقط على شكل فجوات في التمثيل البياني للدالة؛ لأن الدالة تكون غير معرّفة عند تلك النقاط ومُعرفةً حولها. مفهوم أساسي نقطة الانفصال a(x) b(x) التعبير اللفظي: إذا كانت - = (f(x، حيث 0 (x) ، وكان - x عاملًا مشتركا بين (x) و (x) ، فإنه توجد نقطة انفصال عندما x = c . +f(x) x أضف إلى طويتك 94 مثال: الفصل 5 العلاقات والدوال النسبية f(x) = (x + (2)(x + 1) x+1 =x+2, x-1 نقطة الانفصال هي: (-1, f(-1)) = (-1, 1) 0 |f(x) = (x + 2) ( x + 1) x+1 وزارة التعليم Ministry of Education 2024-1446

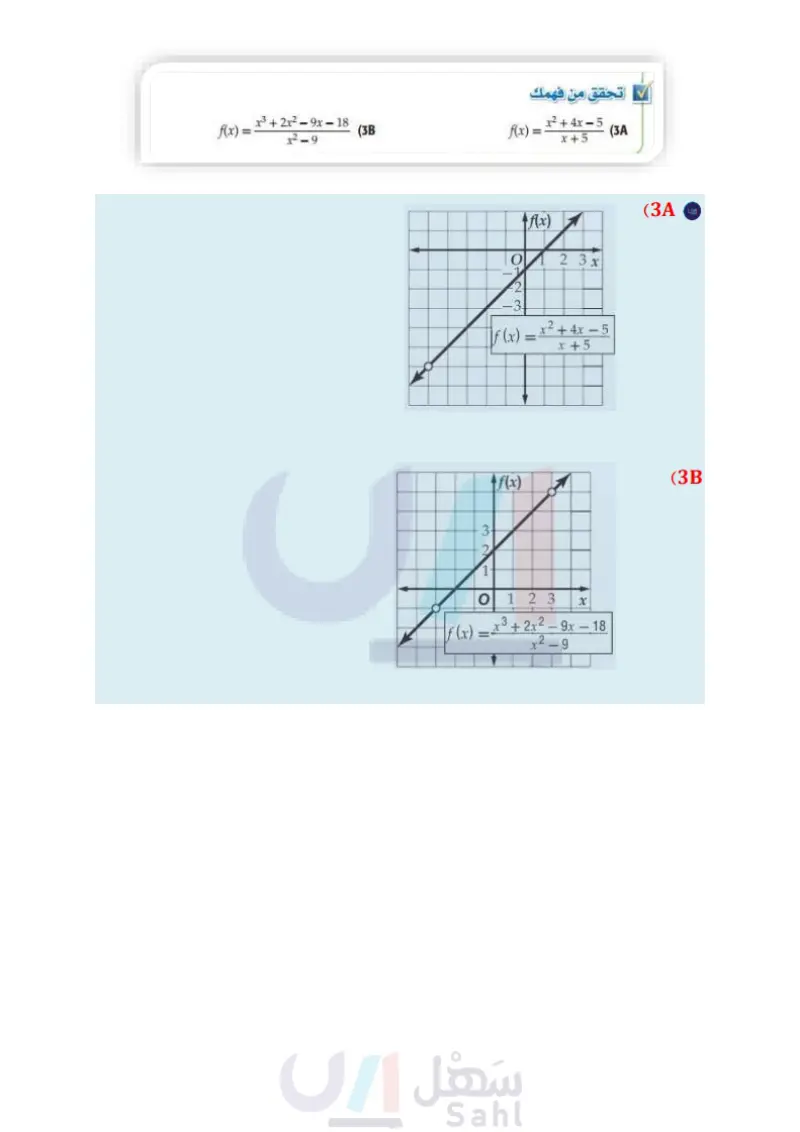
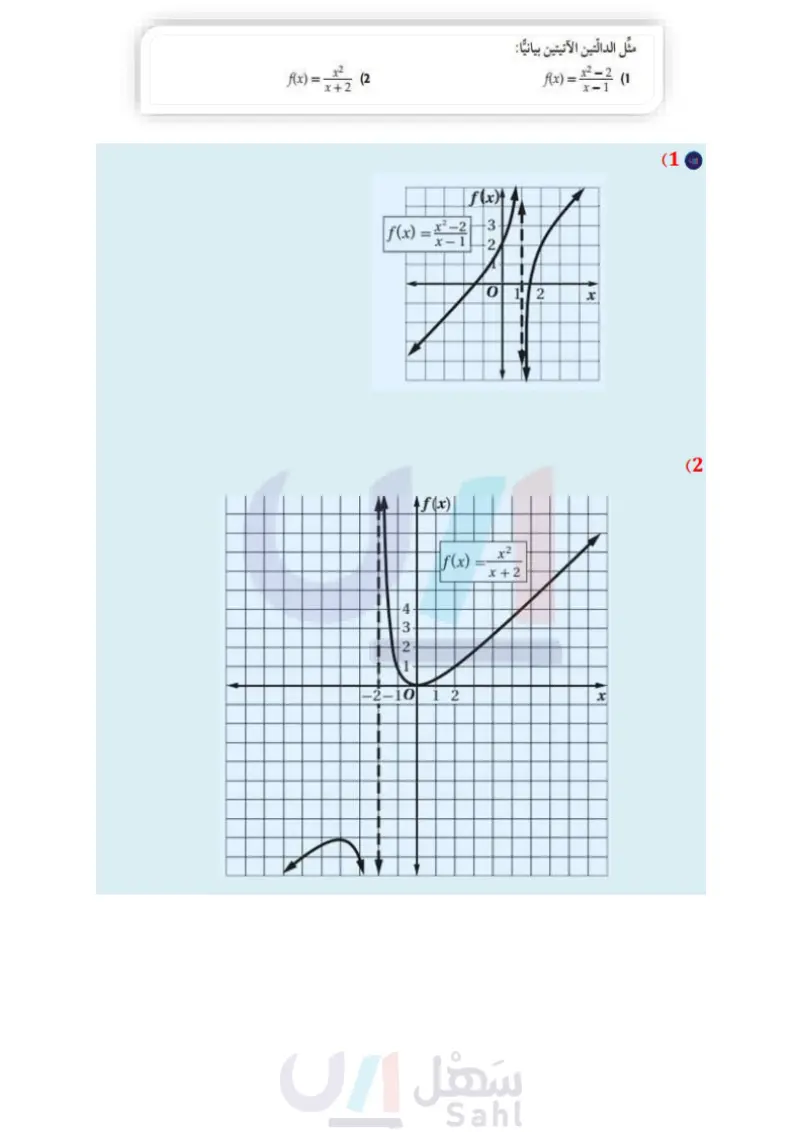
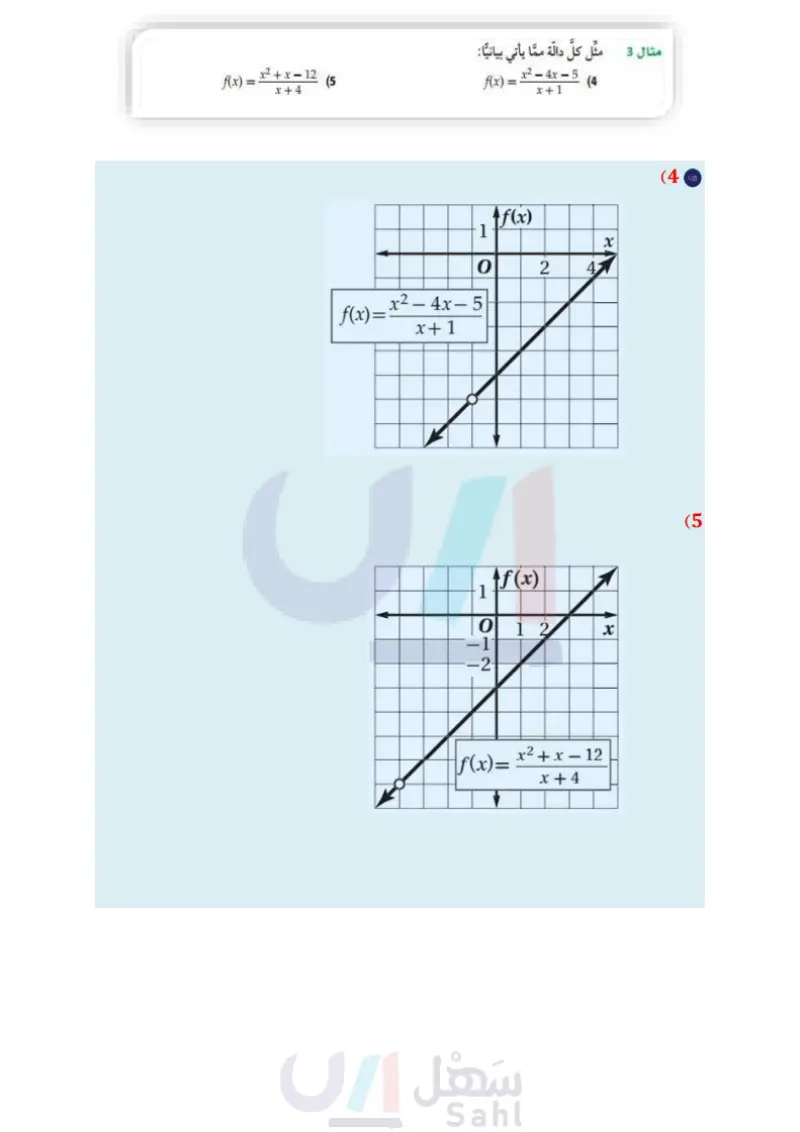
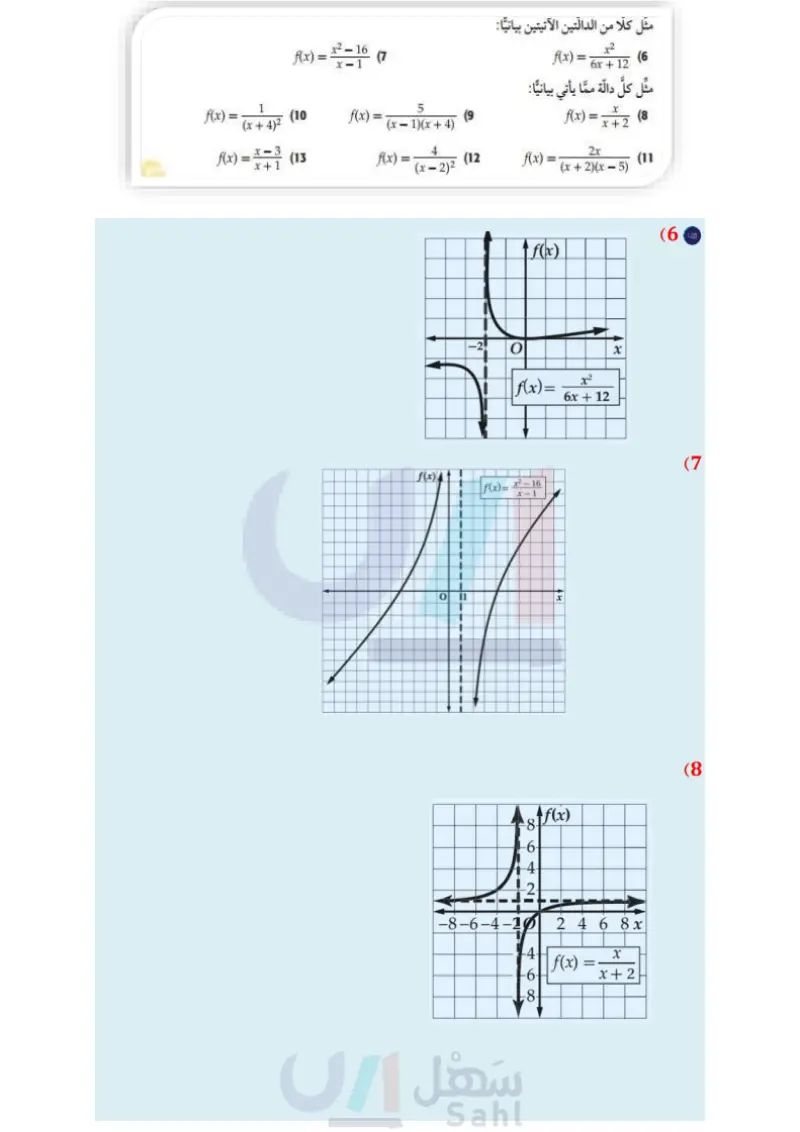
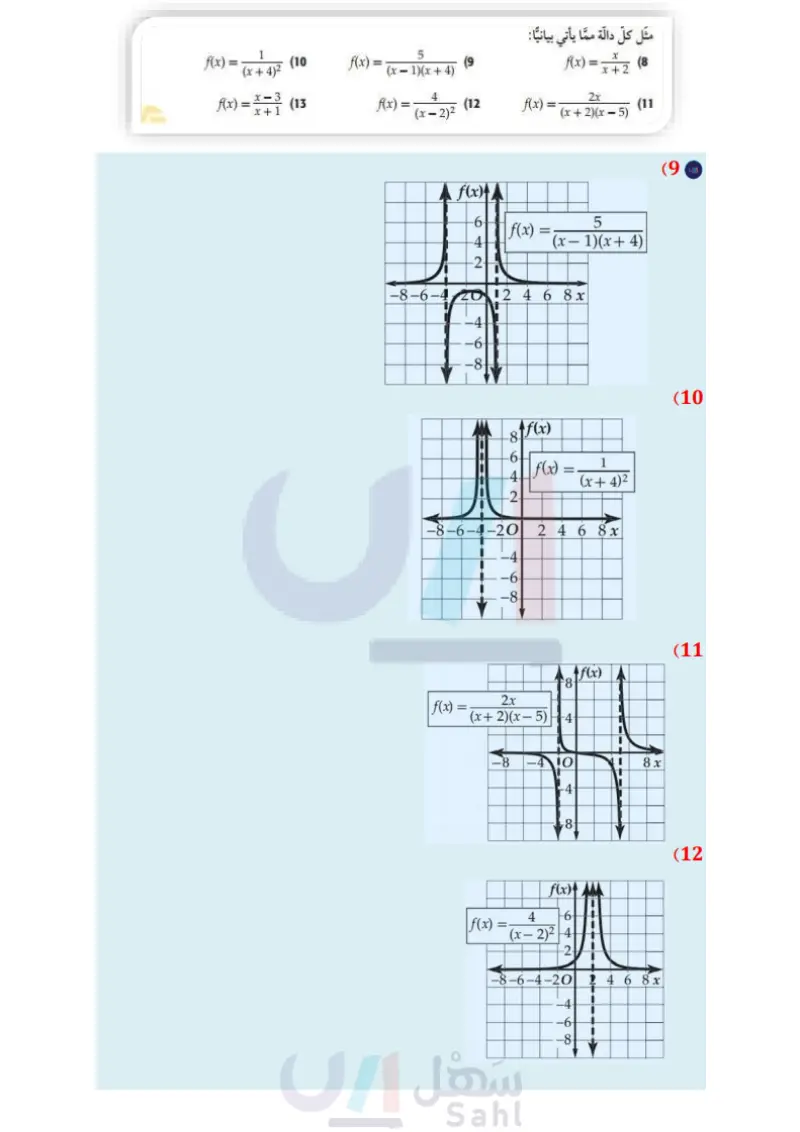
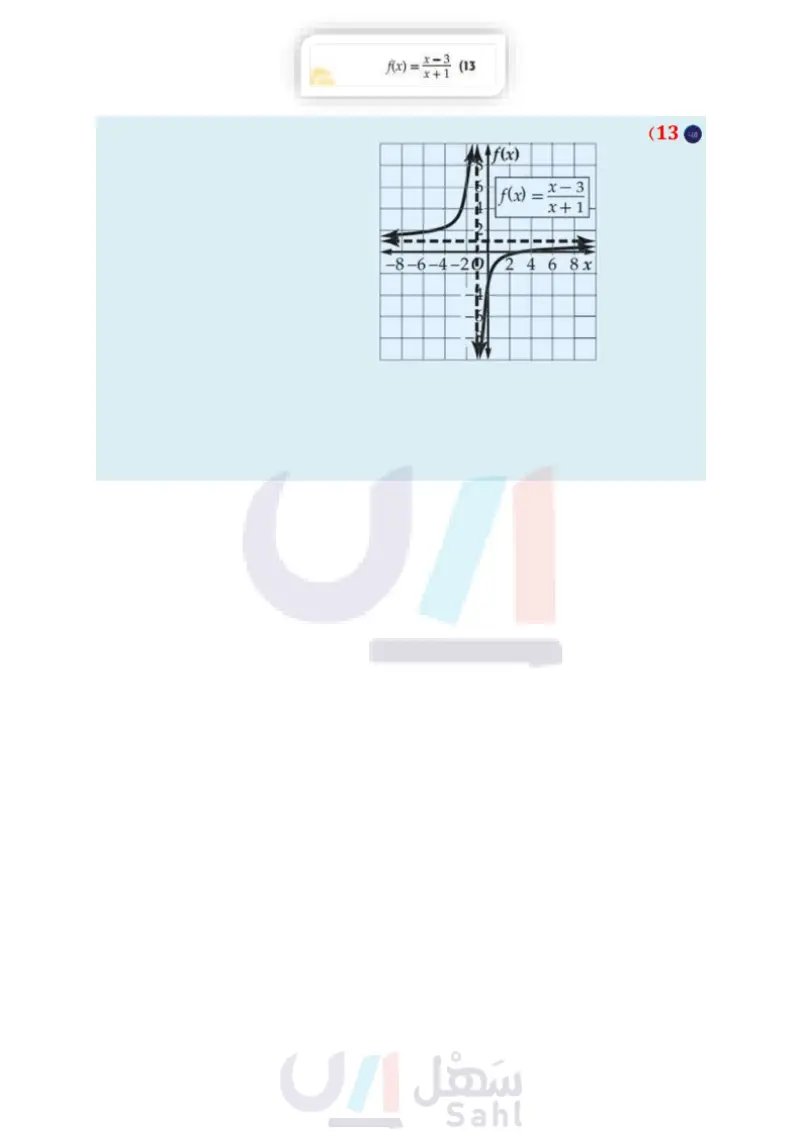
مثال 3 التمثيل البياني لدالة تتضمن نقطة انفصال مثل الدالة 16 - * = (f(x بيانيا . x-4 لاحظ أن مجال الدالّة (x) هو مجموعة الأعداد الحقيقية ما عدا 4 تنبيه ! فجوات التمثيل البياني تذكر أن وجود عامل مشترك بين البسط والمقام يدل على وجود فجوة في التمثيل البياني للدالة. =x+4 x²-16 (x+4)(114) x-4 لذا فإن التمثيل البياني ! x2 - للدالة 16 - x-4 = (f(x هو نفسه التمثيل البياني للدالة 4 + f(x) = x، مع وجود فجوة في التمثيل البياني للدالة 4 + f(x) = x عندما 4 = x . تحقق من فهمك f(x) = x2 + 4x - 5 x+5 (3) تأكد 10 82 Ax) x2 - 16 مثال 1 مثل الدالّتين الآتيتين بيانيا : مثال 2 f(x) = x²-2 (1 f(x) = x3 + 2x2 - 9 - 18 x²-9 (38) f(x) = =x22 (2 (3) كرة سلة: في بداية تدريب لفريق كرة سلة، أحرز سعيد 7 أهداف من 11 رمية حرة لعبها، ويرغب في 7+x تحسين النسبة المئوية للأهداف التي يحرزها والممثلة بالدالة : الأخرى التي سيلعبها . a) مثل هذه الدالة بيانيا. أي جزء من التمثيل البياني للدالة منطقي في سياق المسألة؟ ماذا يمثل مقطع المحور الرأسي للتمثيل البياني؟ (x)، حيث x عدد الرميات الحرة ما معادلة خط التقارب الأفقي؟ وما النسبة المئوية التي يمثلها؟ وهل يمكن الوصول إلى هذه النسبة؟ مثال 3 مثْل كلَّ دالة ممَّا يأتي بيانيا : تدرب وحل المسائل f(x) = x²-4x-5 x+1 (4 مثال 1 مثل كلا من الدالّتين الآتيتين بيانيا: (6 2 6x + 12 f(x) = مثال 2 مثل كلَّ دالة ممَّا يأتي بيانيا : f(x) = x2 + x - 12 x+4 (5 f(x) = 12-16 (7 f(x) = . (10 5 f(x) = (9 (x+4)² (x-1)(x+4) f(x) = x+2 (8 f(x) = x-3 (13 x + 1 f(x)= 2x (12 (x-2)² f(x)= (11 (x+2)(x-5) وزارة التعليم الدرس 4-5 تمثيل الدوال النسبية بيانيا 95 2024-1446

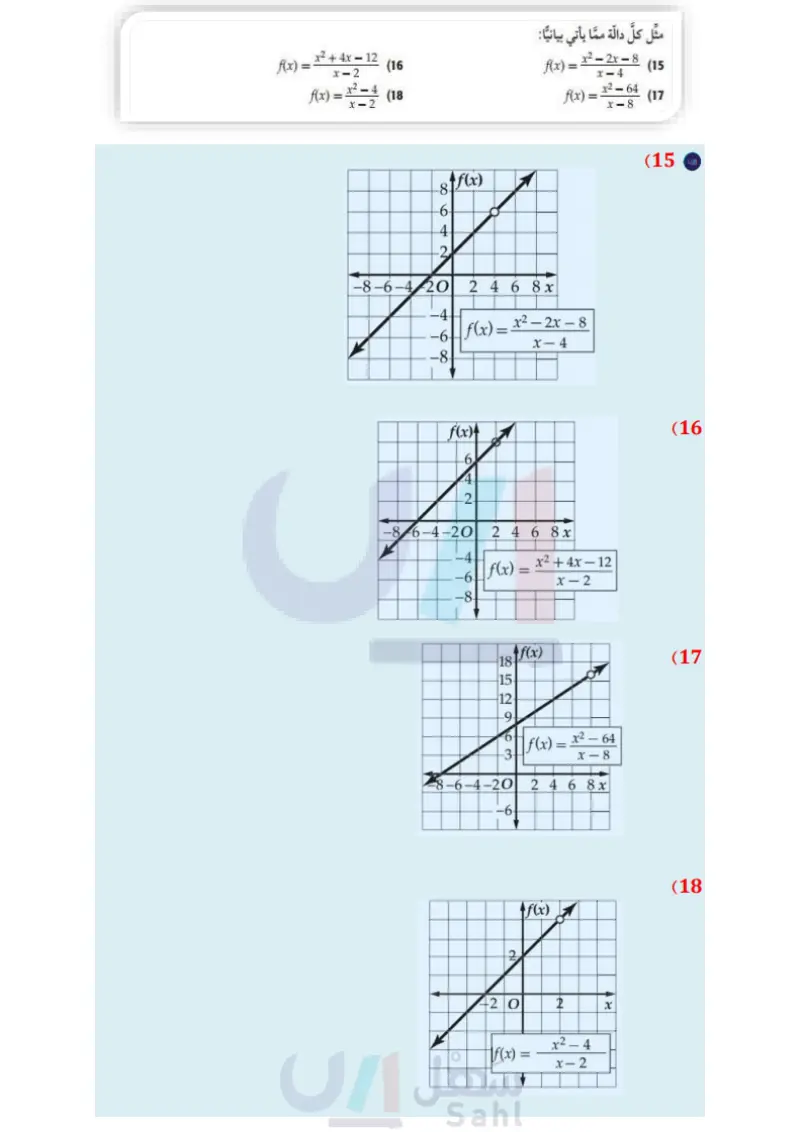
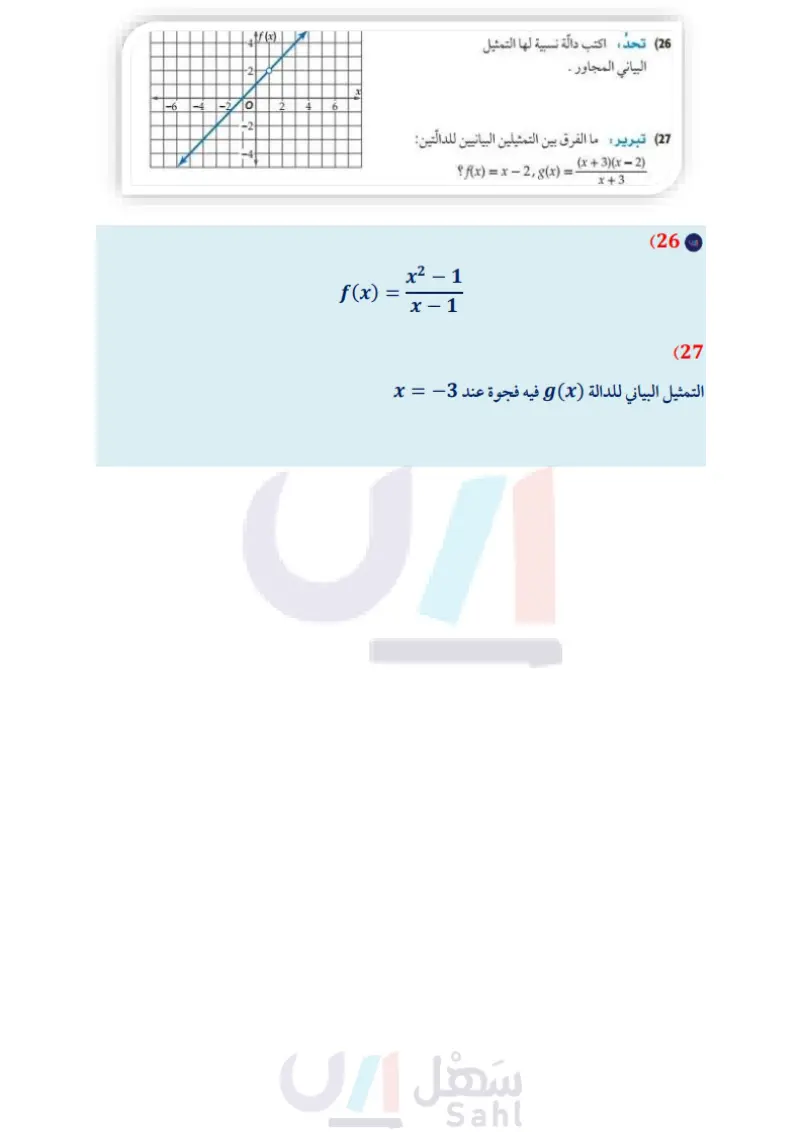
14) كهرباء دائرة كهربائية تحتوي على 3 مقاومات موصولة على التوالي، وتُعطى شدة التيار الكهربائي بالأمبير - = C ، حيث V فرق الجهد بالفولت و R1, R2, R المقاومات بالأوم. فيها بالمعادلة V R1 + R2 + R3 a إذا كان هو المتغير المستقل، و C هو المتغير التابع فمثل المعادلة بيانيًا عندما تكون . V = 120 v, R2 = 252, R3 = 75 2 ) اكتب معادلة خط التقارب الرأسي، وأوجد مقطع المحور R، ومقطع المحور C للتمثيل البياني. أوجد قيمة C عندما تكون 1402 = R1 . ما قيم المجال والمدى المنطقية في سياق المسألة؟ مثال 3 مثل كلَّ دالة مما يأتي بيانيا : f(x)== x2 + 4x - 12 x-2 (16 f(x)= 2-4 (18 x2 - 21 - 8 f(x)= (15) x-4 x²-64 f(x)= (17 x - 8 أوجد معادلات خطوط التقارب الرأسية، ونقط الانفصال (إن وجدت) للتمثيل البياني لكل دالة مما يأتي: f(x)= = 5 (21 f(x) = 2 (20 x2 + 3x x+4 f(x)= (19 x2 + 9x+20 (22) اتصالات اشترى أحمد هاتفًا محمولا مزودًا بخدمة إنترنت، وكان ثمن الهاتف 1500 ريال، ومتوسط تكلفة مكالماته الشهرية 200 ريال بالإضافة إلى 100 ريال شهريا لخدمة الإنترنت. إذا علمت أن التكلفة الشهرية لأحمد تشمل : ثمن الهاتف، ومتوسط تكلفة المكالمات، وثمن خدمة الإنترنت. a اكتب دالة نسبية تمثل متوسط التكلفة الشهرية لأحمد ، بعد مرور x شهرًا من شراء الهاتف، ومثلها بيانيا. اكتب معادلات خطوط تقارب التمثيل البياني للدالة؟ لماذا يكون الربع الأول من المستوى الإحداثي هو المهم في هذا الموقف؟ بعد كم شهر من شراء الهاتف يكون متوسط التكلفة الشهرية لأحمد 450 ريالًا ؟ مثْل كلَّ دالّة مما يأتي بيانيًّا: الربط بالحياة أشار مسح عالمي إلى أن مستخدمي الهواتف النقالة في المملكة العربية السعودية أكثر (23 f(x)= x+1 x2 + 6x + 5 من أي دولة في العالم بمعدل مسائل مهارات التفكير العليا 180 هاتفا نقالا لكل 100 فرد المصدر، وزارة الاتصالات وتقنية المعلومات http://www.mcit.gov.sa/Ar/ Communication f(x) = x2 - 10 - 24 x+2 (24 25) مسألة مفتوحة مثل بيانيًا بشكل تقريبي دالّة نسبية لها خط تقارب أفقي معادلته 1 = y، وخط تقارب رأسي معادلته 2 = x . (26) تحد: اكتب دالة نسبية لها التمثيل البياني المجاور . if (x) وزارة التعليم Ministry of Education 2024-1446 6 27 تبرير ما الفرق بين التمثيلين البيانيين للدالّتين: f(x)=x-2, g(x) = (x+3)(x-2) x+3 الفصل 5 العلاقات والدوال النسبية 96

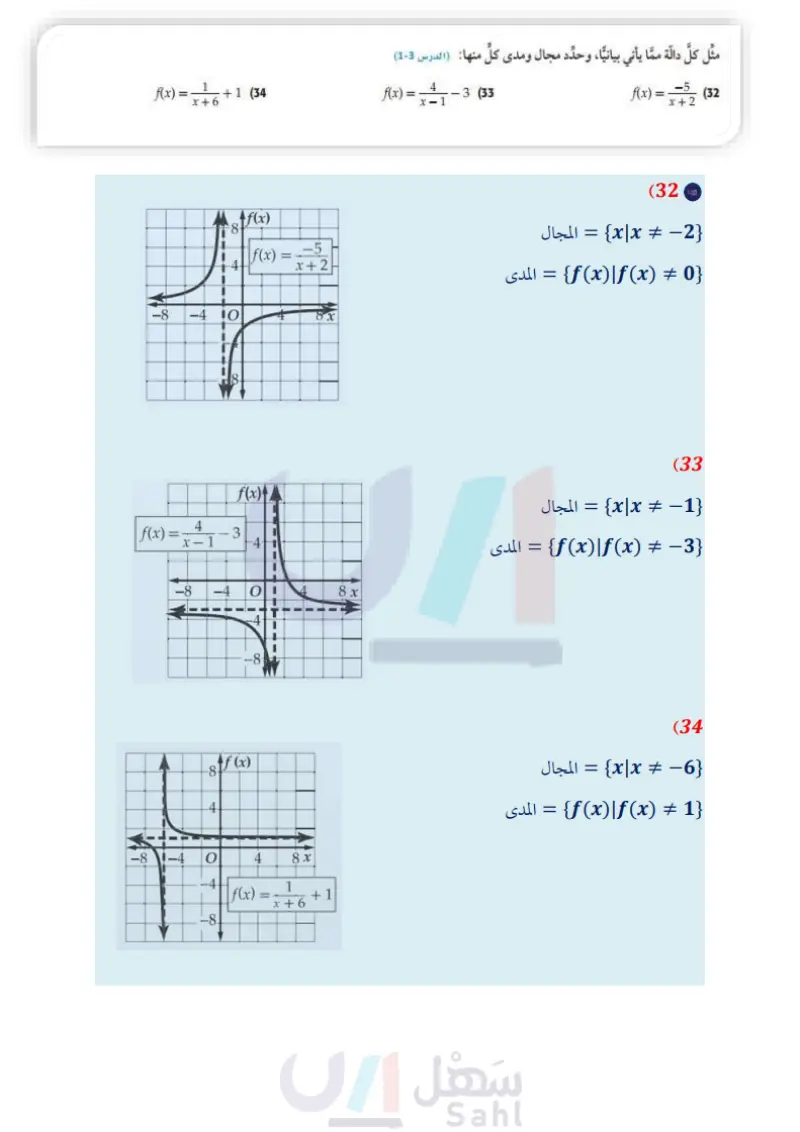
(28) برهان: إذا علمت أن الدالّة النسبية هي د دالة على الصورة (f(x) حيث (x) و (x) كثير تا حدود و 0 (x)، فأثبت أن f(x) = 1 + c دالة نسبية. a(x) b(x) (29) اكتب وضّح كيف يمكن استعمال تحليل البسط والمقام إلى عوامل لإيجاد خطوط التقارب الرأسية أو نقطة الانفصال الدالة نسبية. 40° to تدريب على اختبار (30) يريد علي أن يختار كتابين معًا من بين 6 كتب مختلفة. بكم طريقة (31) هندسة في الشكل المجاور، يمكنه القيام بذلك؟ ما قيمة 1 + x + y + x ؟ 140 A 280 B 320 C 360 D 48 A 18 B 15 C 12 D مراجعة تراكمية مثل كل دالة مما يأتي بيانيا، وحدد مجال ومدى كل منها: (الدرس (3-5) f(x)= +1 (34 f(x) = x+6 = x + 1-3 (33 الزمن المسافة (km) (h) 0 0 55 1 110 2 165 3 165 4 225 5 d-4 d² +2d-8 d+2 + (36 2 - 16 5 + x²-3x-28 7 2x-14 (38 وزارة التعليم الدرس 4-5 تمثيل الدوال النسبية بيانيا 97 2024-1446 f(x)= x+2(32 بسط كل عبارة مما يأتي: (الدرس (2-5) m + m2 - 4 2 3m+6 (35 y 614 (37 y+3 12 - 9 (39) سفر يبين الجدول المجاور المسافات التي يقطعها أحمد عند سفره إلى مدينة مجاورة بعد مرور زمن معين (مهارة سابقة) a أوجد معدل تغير المسافة بين الساعتين الأولى والثالثة من الانطلاق. أوجد معدل تغير المسافة بعد مرور 5 ساعات من الانطلاق.