الأسس النسبية - رياضيات2-2 - ثاني ثانوي

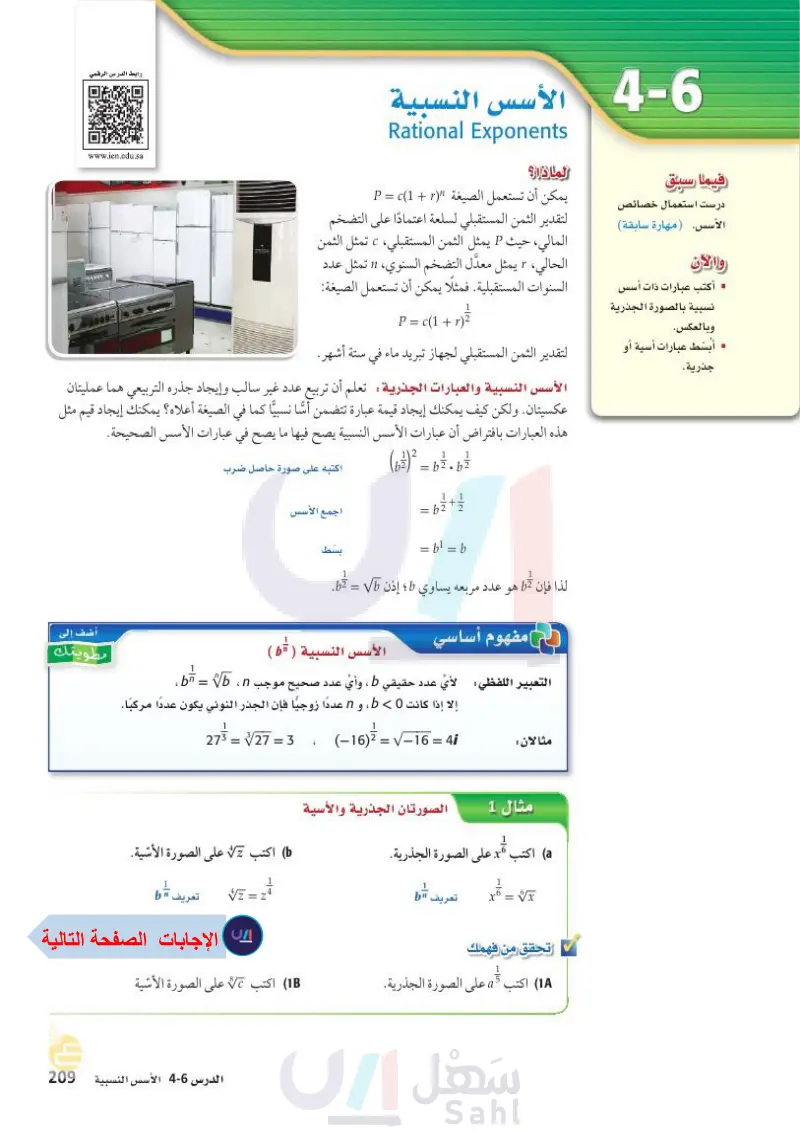
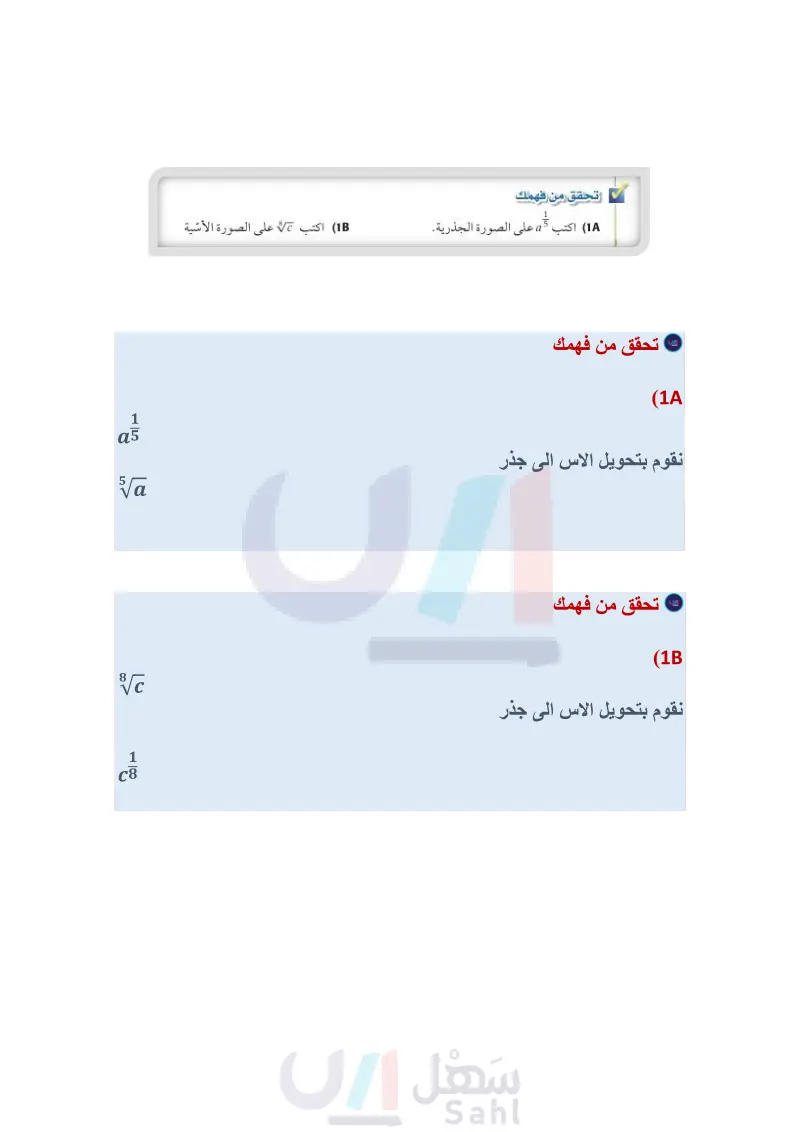
6 الأسس النسبية Rational Exponents رابط الدرس الرقمي www.ien.edu.sa فيما سبق درست استعمال خصائص لماذا؟ يمكن أن تستعمل الصيغة ( + 1 = P الأسس (مهارة سابقة) لتقدير الثمن المستقبلي لسلعة اعتمادا على التضخم المالي، حيث P يمثل الثمن المستقبلي، c تمثل الثمن الحالي، r يمثل معدل التضخم السنوي، " تمثل عدد والان أكتب عبارات ذات أسس السنوات المستقبلية. فمثلًا يمكن أن تستعمل الصيغة: نسبية بالصورة الجذرية وبالعكس. . أبسط عبارات أسية أو جذرية. P = c(1+r)²² لتقدير الثمن المستقبلي لجهاز تبريد ماء في ستة أشهر. الأسس النسبية والعبارات الجذرية : تعلم أن تربيع عدد غير سالب وإيجاد جذره التربيعي هما عمليتان عكسيتان. ولكن كيف يمكنك إيجاد قيمة عبارة تتضمن أسا نسبيا كما في الصيغة أعلاه؟ يمكنك إيجاد قيم مثل هذه العبارات بافتراض أن عبارات الأسس النسبية يصح فيها ما يصح في عبارات الأسس الصحيحة. (b²)² = b²².b²² اكتبه على صورة حاصل ضرب = b}+} اجمع الأسس = bi = b بسط لذا فإن b هو عدد مربعه يساوي b ؛ إذن b = Vb. مفهوم أساسي الأسس النسبية (b) .b التعبير اللفظي لأي عدد حقيقي ، وأي عدد صحيح موجب b = b ، n ، إلا إذا كانت 0 b و n عدداً زوجيًا فإن الجذر النوني يكون عدداً مركباً. مثالان 27 =√√27=3 < (-16) =√-16=41 مثال 1 الصورتان الجذرية والأسية 26 اكتب على الصورة الجذرية. اكتب 2 على الصورة الأسية. V = z تعریف تعريف 11 b تحقق من فهمك 1) اكتب 3 على الصورة الجذرية. 1 اكتب على الصورة الأسية أضف إلى نك مطوية وزارة التعليم الدرس 6-4 الأسس النسبية 43 2024-1446

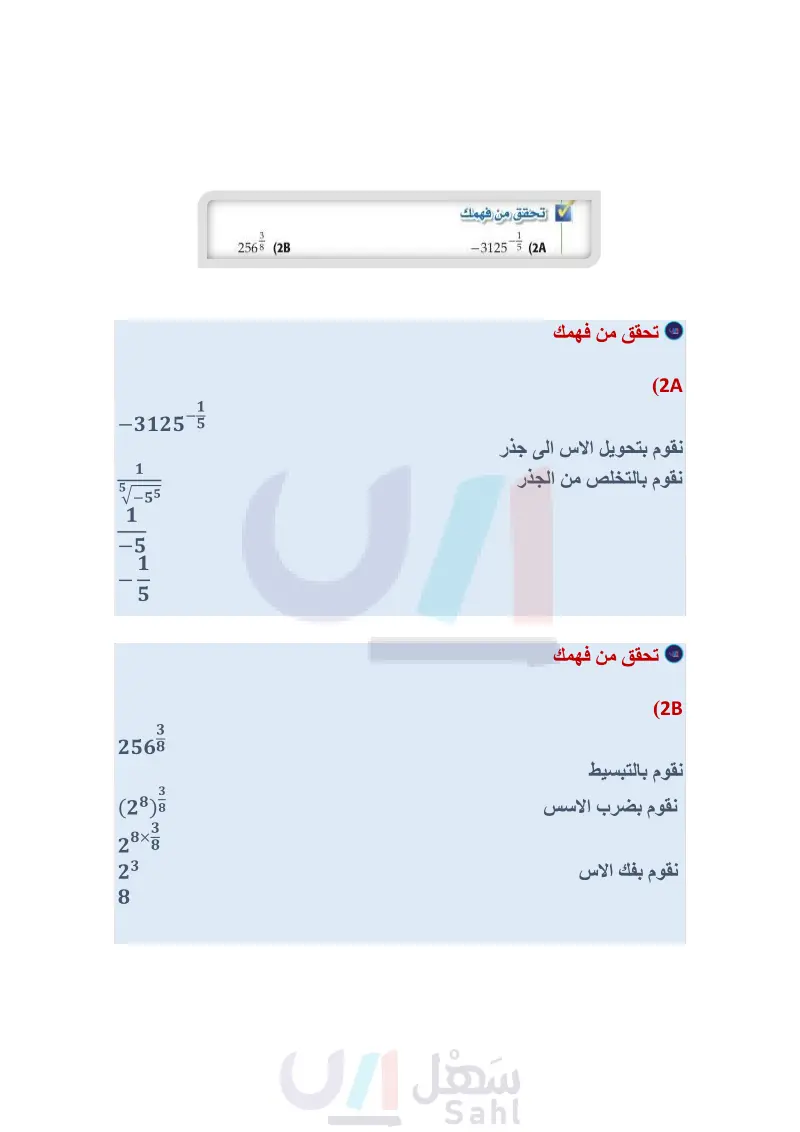
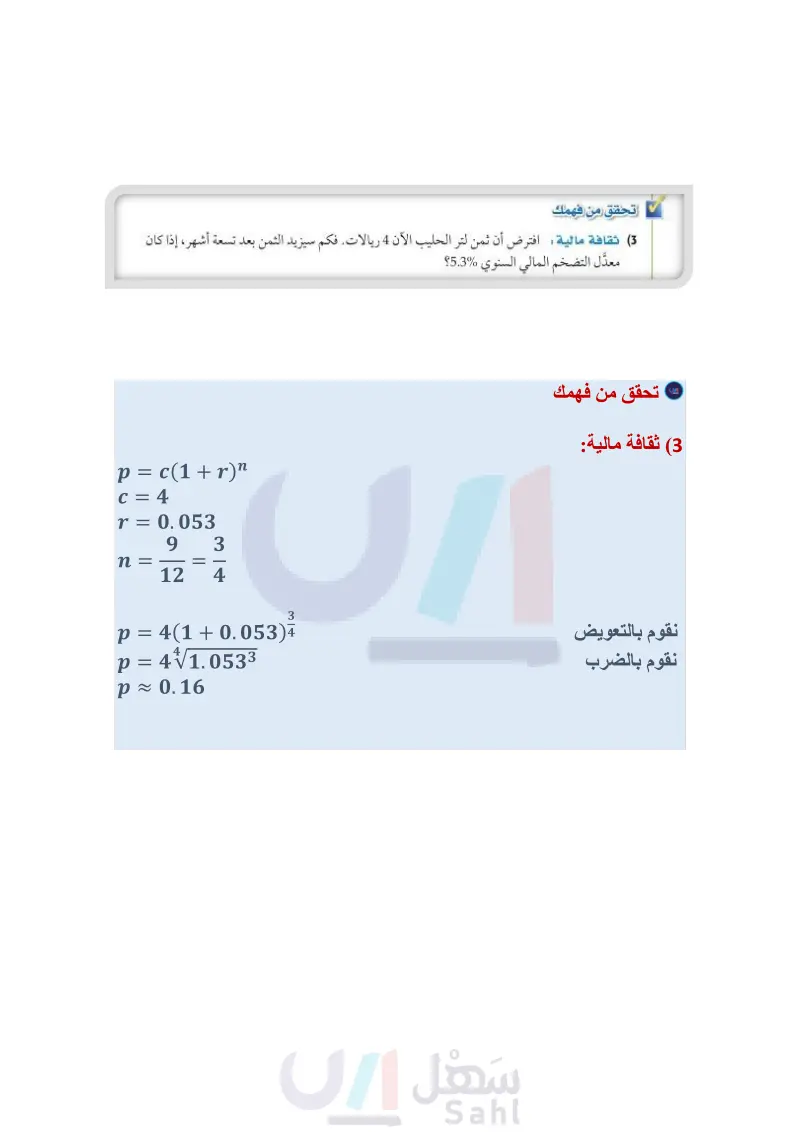
وبشكل عام يمكنك تقديم التعريف العام الآتي للأسس النسبية : مفهوم أساسي الأسس النسبية (b) أضف إلى طويتك التعبير اللفظي يكون " ( b = Vbx = V لأي = عدد حقيقي 6 لا يساوي صفرا ، ولأي عددين صحيحين , بحيث 1 ، إلا إذا كانت 0 > b و y عددًا زوجيا، فإن الجذر قد يكون عددًا مركبا. 273 = (27) = 32 = 9 (16) = (16) 3 = (41) 3 = - 64i مثالان: كما أن القواعد التي تنطبق على الأسس الصحيحة السالبة تنطبق أيضًا على الأسس النسبية السالبة. مثال 2 إيجاد قيم عبارات تتضمن أسسا نسبية أوجد قيمة كل عبارة مما يأتي: 81(a 2163 (b 216 = 63 2163 (63)3 = b-n = 1 81 خاصية قوة القوة ضرب الأسس بسط 63 1 bn 814 √√81 814 1 √81 = 62 1 81=34 √√34 = 36 بسط 256 (28) تحقق من فهمك -3125 (2) مثال 3 من واقع الحياة حل معادلات تتضمن أسسا نسبية ثقافة مالية: ارجع إلى الفقرة الواردة في بداية الدرس ، وافترض أن الثمن الحالي لجهاز تبريد الماء هو 390 ريالا. فكم سيزيد الثمن خلال ستة أشهر إذا كان معدل التضخم المالي السنوي %5.3 ؟ c=390, r=0.053, n = الصيغة 2 6 أشهر 12 شهرا استعمل الحاسبة P = c(1+r)" 390(1+0.053)² ≈ 400.20 10.20 390.00 - 400.20 إذن سيزيد ثمن جهاز تبريد الماء بعد ستة أشهر بمقدار 10.20 ريالات تقريباً. تحقق من فهمك (3) ثقافة مالية : افترض أن ثمن لتر الحليب الآن 4 ريالات. فكم سيزيد الثمن بعد تسعة أشهر، إذا كان معدل التضخم المالي السنوي %5.3؟ تبسيط العبارات خواص الأسس التي تعلمتها سابقا تنطبق أيضًا على الأسس النسبية؛ لذا اكتب كل عبارة على صورة أسس موجبة واحرص على أن تكون الأسس في مقام الكسر أعدادًا صحيحة موجبة؛ لذلك أنت في حاجة إلى إنطاق المقام أحيانًا. وزارة التعليم Ministry of Education 2024-1446 الفصل 4 العلاقات والدوال العكسية والجذرية 44

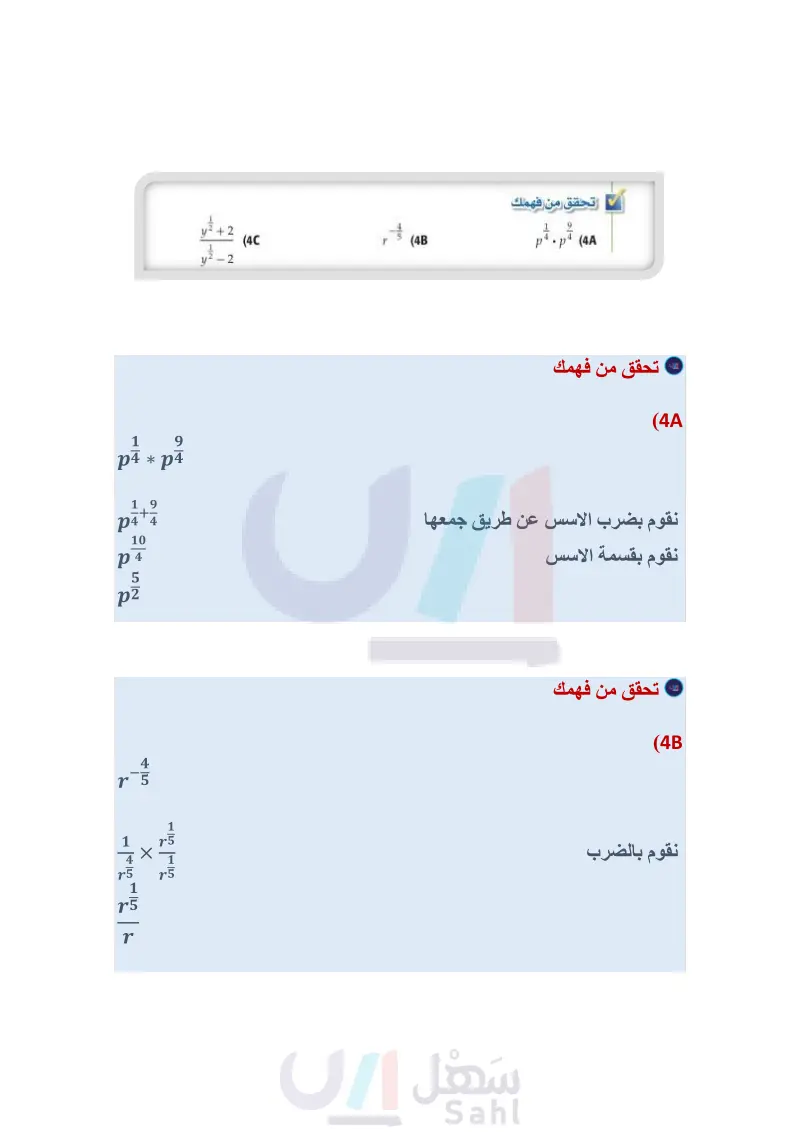
b-n=1 Ъп اضرب في b. b = b+ b = b = b (AC b (b مثال 4 تبسيط عبارات بأسس نسبية بسط كل عبارة مما يأتي: خاصية ضرب القوى جمع الأسس (c 3x2 + 2 2 3x2 + 2 3x2 + 2 3x²-2 - 2 - 3 مرافق ( 2 + 37 اضرب بسط (4B 3x2 - 8x2 + 4 9x24 1 3x - 8x2 + 4 9x-4 تحقق من فهمك 1 9 p¹.p³¹³ (4A عند تبسيط عبارة جذرية اجعل دليل الجذر أقل ما يمكن. وتذكّر أن استعمال الأسس النسبية يسهل هذه العملية، وبعد الانتهاء من استعمال الأسس النسبية، أعد كتابة الناتج في الصورة الجذرية. مثال 5 تبسيط العبارات الجذرية بسط كل عبارة مما يأتي: وزارة التعليم √√982 (b الأسس النسبية 92) = 92 الأسس النسبية 9g2 = (3g) 2 = [(38) 2 27=33 خاصية قوة القوة = (38) خاصية قوة القوة الدرس 6-4 الأسس النسبية 45 2024-1446 √√27 √27 √3 إرشادات للدراسة. تبسيط العبارات عند تبسيط عبارات تحوي أسسا نسبية اترك الأسس على الصورة النسبية بدلا من كتابة العبارة على الصورة الجذرية.

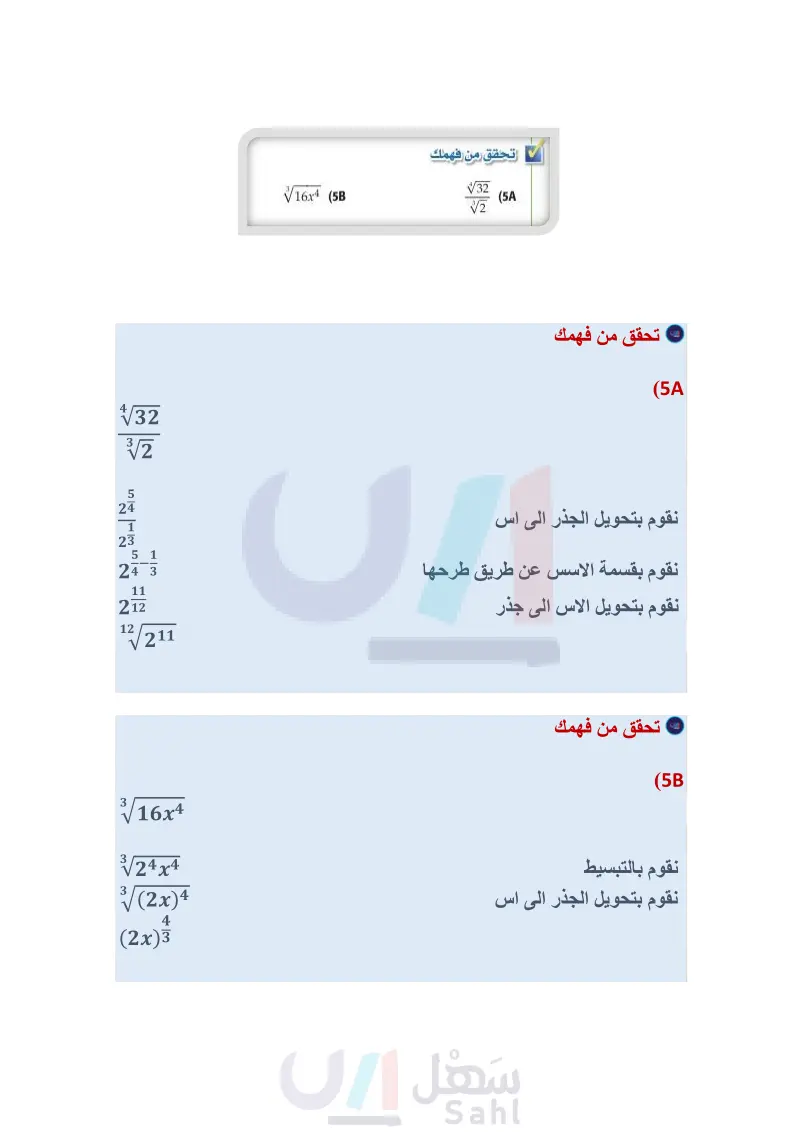
خاصية قسمة قوتين = بسط إرشادات للدراسة = √√3 أعد كتابة العبارة على الصورة الجذرية العبارات الجذرية تحقق من فهمك والأسية 46 أعد كتابة العبارة على الصورة الجذرية اكتب العبارة بعد تبسيطها (الناتج النهائي) على الصورة التي كان عليها قبل التبسيط؛ أي إذا بدأت بعبارة جذرية، فاكتب الناتج النهائي على الصورة الجذرية وإذا بدأت بعبارة تتضمن أسسا نسبية فاكتب الناتج النهائي على الصورة الأسية √32 (5) √2 ملخص المفاهيم √16x4 (5B عبارات تتضمن أسسا نسبية تكون العبارات التي تتضمن أسسًا نسبية في أبسط صورة إذا تحققت الشروط الآتية: . جميع الأسس غير سالبة . جميع الأسس في المقام هي أعداد صحيحة موجبة . لا يتضمن أي من البسط أو المقام أو كليهما كسرا. . دليل الجذر أو الجذور المتبقية فيها أصغر ما يمكن. أضف الى مطوع مثال 1 اكتب العبارة الأسية على الصورة الجذرية، والعبارة الجذرية على الصورة الأسية في كل مما يأتي: 104 (1 مثال 2 أوجد قيمة كل عبارة مما يأتي: 3433 (5) (2 32 (6) √15 (3 √√7x69 (4 125 1253 (7 (8 1 42 مثال 3 9) قياس : إذا علمت مساحة مربع هي ،A ، فإنه يمكن إيجاد طول ضلعه ) باستعمال القانون A2 = . فإذا علمت أن مساحة حديقة مربعة الشكل 169m2، فما طول ضلعها ؟ المثالان 4 بسط كل عبارة مما يأتي: تدرب وحل المسائل (12 (11 .² (10 √√64 (15 (14 √√64z6 (13 g2+1 مثال 1 اكتب العبارة الأسية على الصورة الجذرية، والعبارة الجذرية على الصورة الأسية في كل مما يأتي: 85 (16 √625x2 (19 √17 (18 (x3)2 (17 (-27) (23 16 (22 2564 (21 مثال 2 أوجد قيمة كل عبارة مما يأتي: 273 (20 الفصل 4 العلاقات والدوال العكسية والجذرية وزارة التعليم Ministry of Education 2024-1446

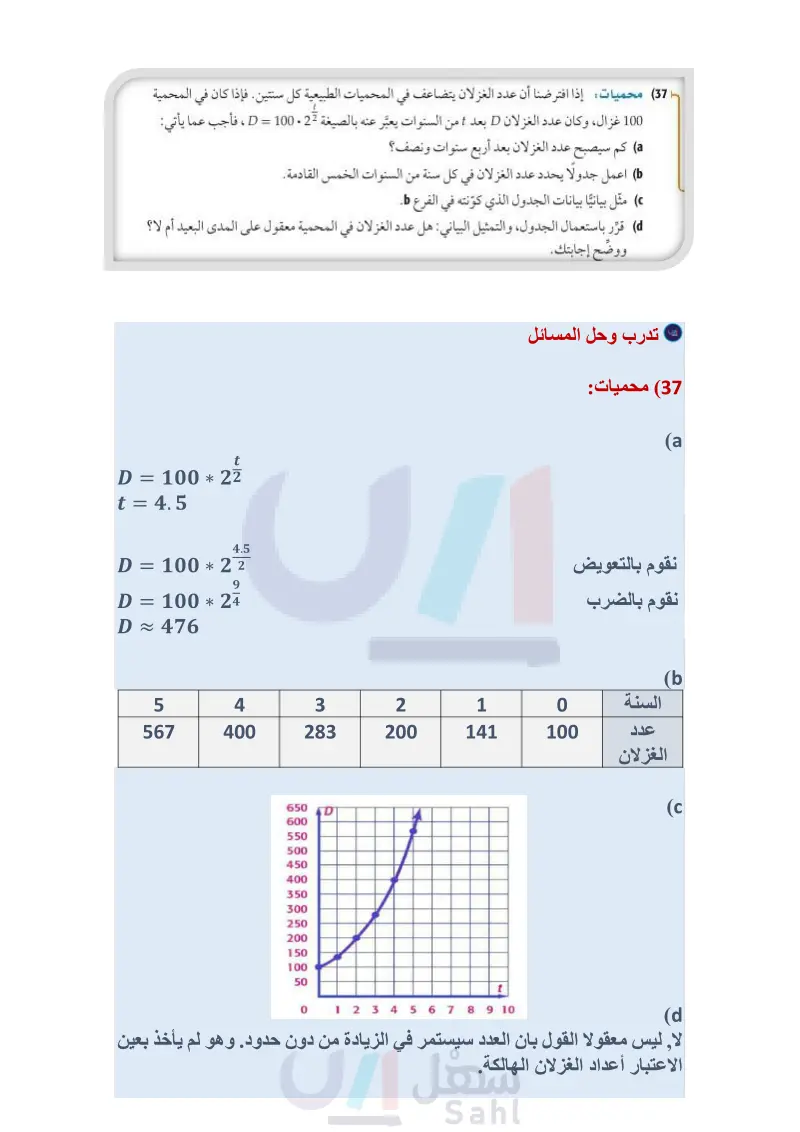
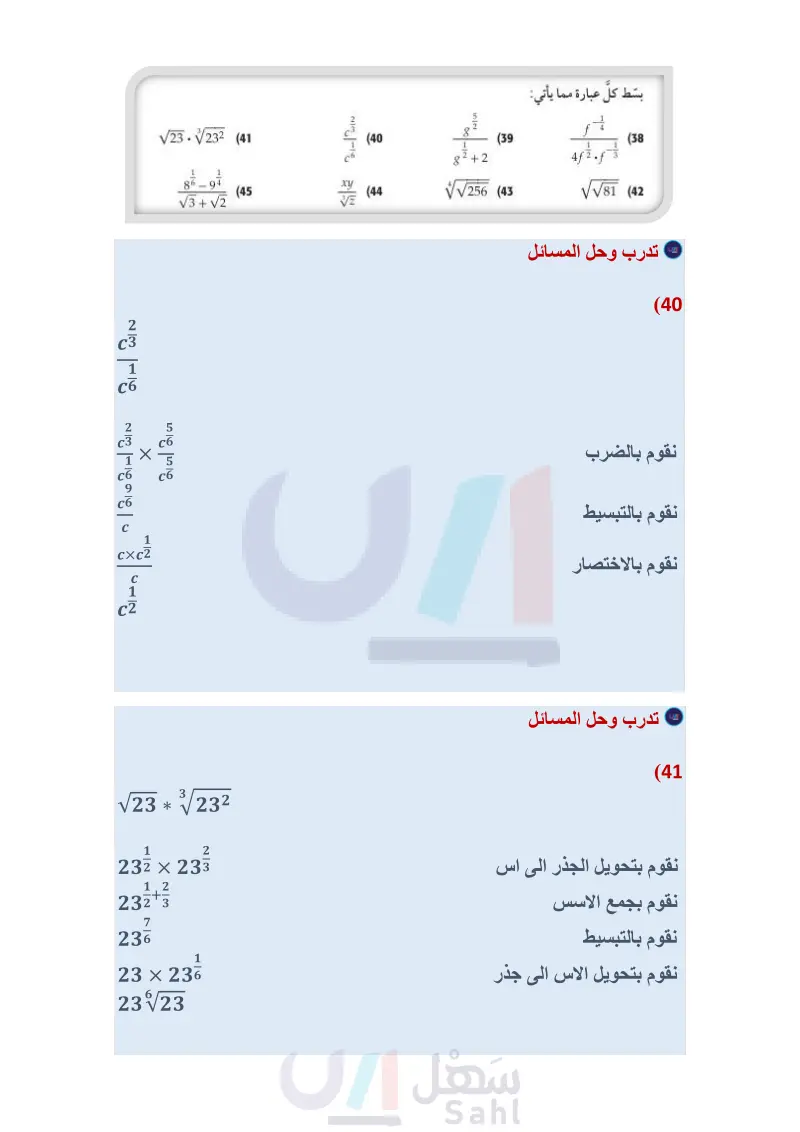
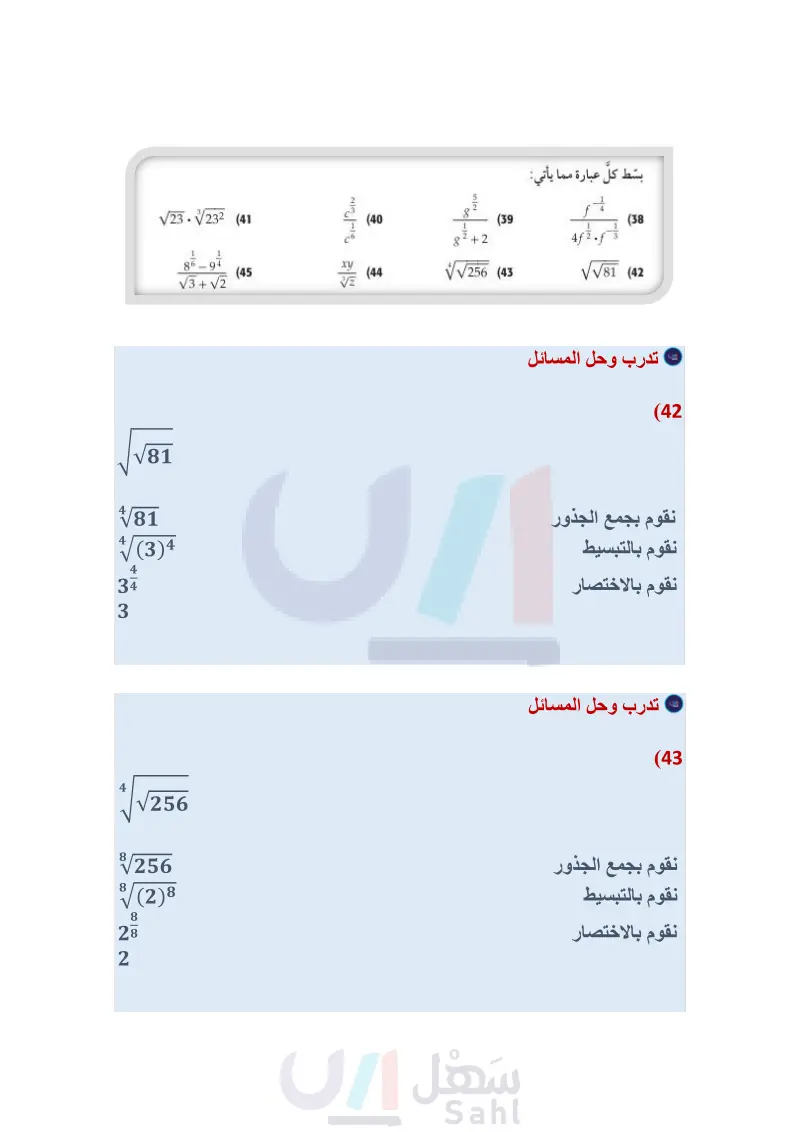
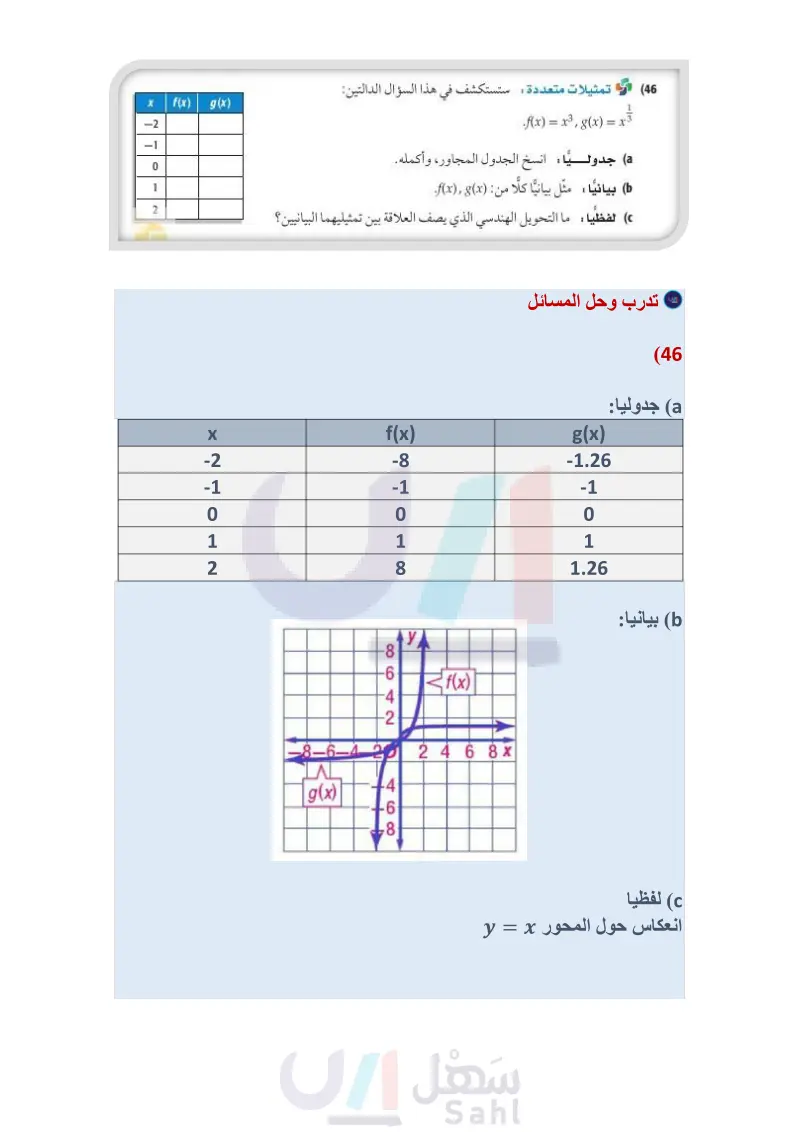
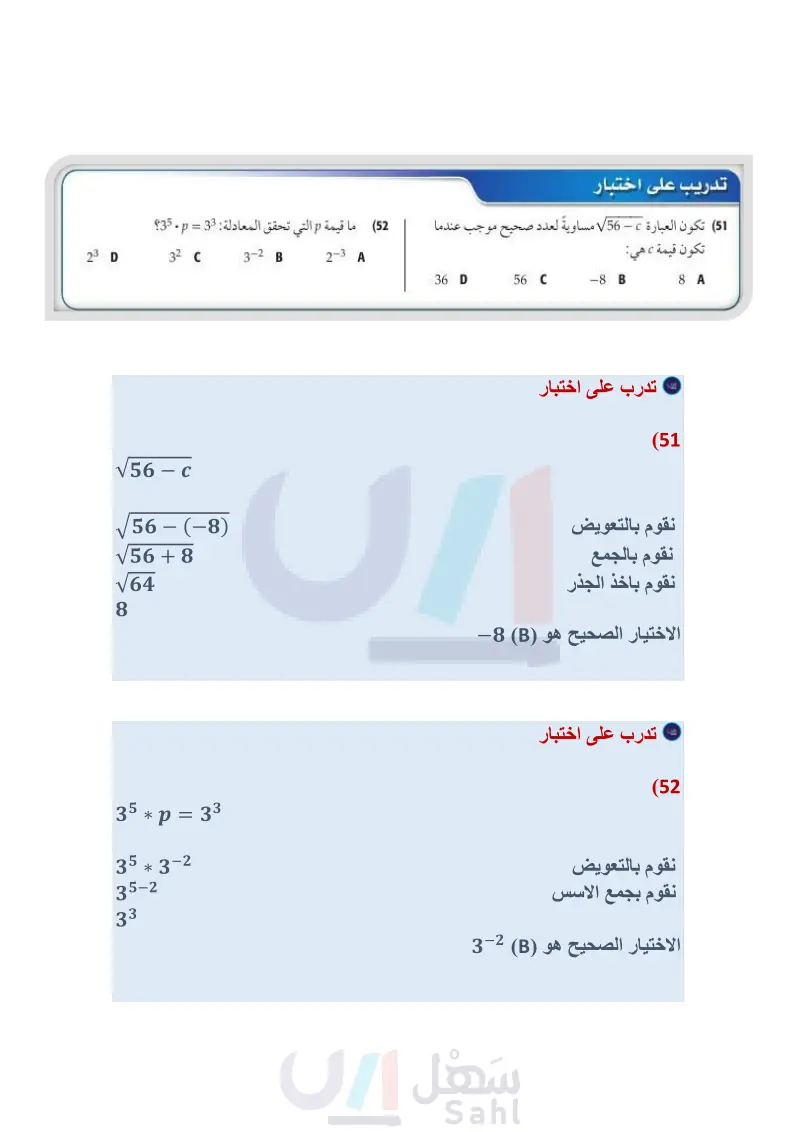
مثال 3 (24) كرة سلة : يوجد حجمان لكرة السلة حجم كبير وآخر صغير، كما في الصورة جانبًا. فإذا كان نصف قطر الكرة r التي تسع V وحدة مكعبة من الهواء يعبر عنه بالعلاقة 3 ) = r ، فأجب عما يأتي: (47) a) أوجد نصف قطر كرة السلة ذات الحجم الصغير. ) أوجد نصف قطر كرة السلة ذات الحجم الكبير. المثالان 45 بسط كل عبارة مما يأتي: (25 (26 هندسة أوجد مساحة كل شكل فيما يأتي: v = 455 in v = 413 in3 (29 √25x2 (28 √81 (27 √√3 2 20 (36 (31 √216 (35 -3w+. (30 1 (32) ما أبسط صورة للعبارة 322 - 22 + 182 ؟ (4-7)=134 بسط كل عبارة مما يأتي: 7 5 a. a4 (33 الربط مع الحياة الطريقة الأكثر دقة لتحديد عمر بعض أنواع الغزلان هي النظر إلى مقطع عرضي (37) محميات: إذا افترضنا أن عدد الغزلان يتضاعف في المحميات الطبيعية كل سنتين. فإذا كان في المحمية 100 غزال، وكان عدد الغزلان D بعد t من السنوات يعبر عنه بالصيغة 22. 100 = D ، فأجب عما يأتي: a كم سيصبح عدد الغزلان بعد أربع سنوات ونصف ؟ اعمل جدولا يحدد عدد الغزلان في كل سنة من السنوات الخمس القادمة. مثل بيانيًا بيانات الجدول الذي كوّنته في الفرع . قرر باستعمال الجدول، والتمثيل البياني: هل عدد الغزلان في المحمية معقول على المدى البعيد أم لا؟ ووضح إجابتك. لإحدى أسنانه، حيث تنمو كل بسط كل عبارة مما يأتي: فصل شتاء طبقة كلسية تكسو السن على شكل حلقة، وكل حلقة تمثل سنة كما هو الحال في حلقات جذع الشجرة (39 (38 g2+2 4f √√√256 (43 √√√√81 (42 √23.√23² (41 (40) 40 (44 و (45 V3 + V2 X f(x) g(x) -2 (46) تمثيلات متعددة ستستكشف في هذا السؤال الدالتين : f(x) = x³, 8(x) = x³½³ a جدوليا : انسخ الجدول المجاور، وأكمله. بيانيا : مثل بيانيا كلا من: (f(x), (x لفظيا : ما التحويل الهندسي الذي يصف العلاقة بين تمثيليهما البيانيين؟ -1 0 1 2 .. وزارة التعليم الدرس 6-4 الأسس النسبية 47 2024-1446

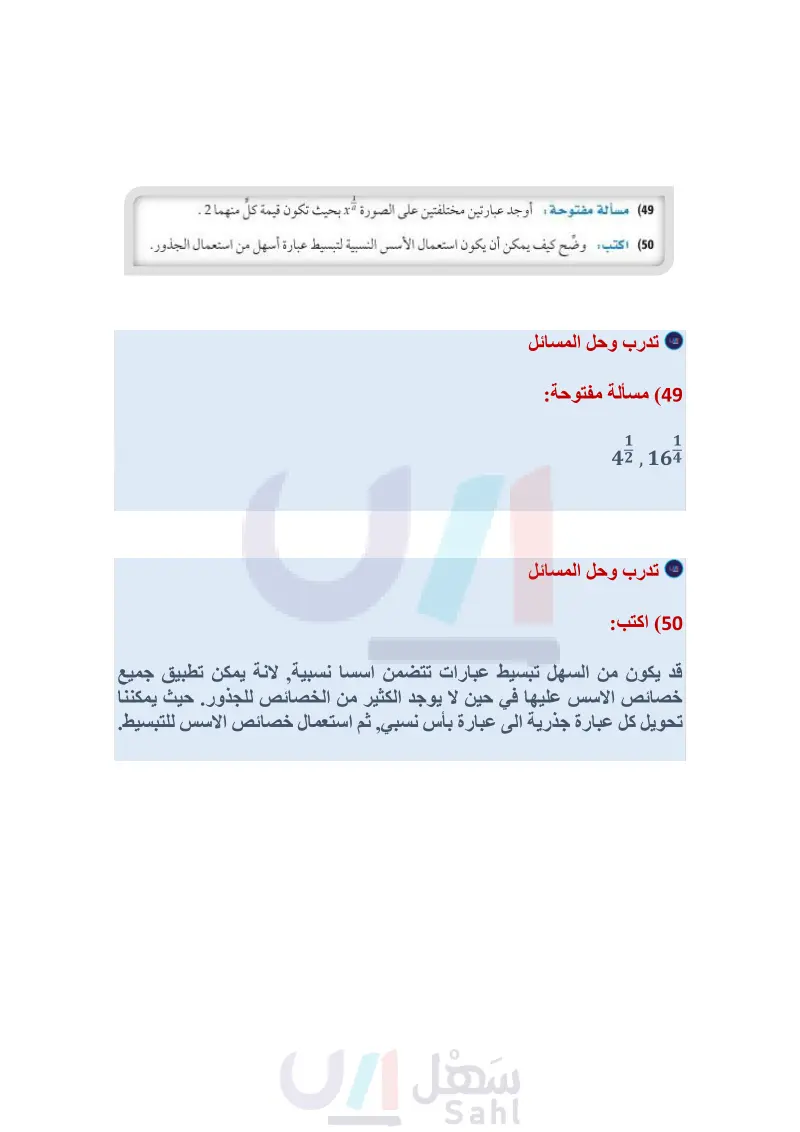
مسائل مهارات التفكير العليا (47) تبرير حدد ما إذا كانت المعادلة -2- (x 2 = (x- صحيحة دائمًا ، أو صحيحة أحيانًا، أو غير صحيحة أبدًا. ووضّح إجابتك. 48) اكتشف الخطأ بسط كل من محمود وعلي العبارة - ، فهل إجابة أي منهما صحيحة؟ محمود علي تدريب على اختبار (49) مسألة مفتوحة : أوجد عبارتين مختلفتين على الصورة x بحيث تكون قيمة كل منهما 2 . 50) اكتب وضح كيف يمكن أن يكون استعمال الأسس النسبية لتبسيط عبارة أسهل من استعمال الجذور. (51) تكون العبارة V56 - c مساويةً لعدد . عندما صحیح موجب تكون قيمة ، هي: 8 A 36 D 56 C -8 B مراجعة تراكمية (52) ما قيمة p التي تحقق المعادلة : 33 = p .35؟ 2-3 A 3-2 B 23 D 32 C بسط كلا مما يأتي: (الدرس: 5-4) √243 (53 √16y³ (54 3√√564623 (55 56) فيزياء : تعطى سرعة الصوت في سائل بالعلاقة V = 1 = 5 ، حيث B معامل تغيّر حجم السائل d كثافة السائل. أما بالنسبة للماء، فإن B = 2.1 × 109N/m2, d = 103kg/m3. أوجد سرعة الصوت في الماء لأقرب متر لكل ثانية (الدرس: 5-4) أوجد ( px ,(4) لكل دالة مما يأتي: (مهارة سابقة) p(x)=x-2 (57 p(x) = x2 + 5 (60) p(x) = x + 4 (58) p(x) = x²-x (61 أوجد () () () () () () () () لكل دالتين فيما يأتي: (الدرس: 1-4) f(x) = - x2 + 6 g(x)=2x²+3x-5 (63 بسط كل عبارة مما يأتي: (الدرس: 5-4) f(x) = 2x2 g(x)=8-x (64 p(x)=6x+3 (59 p(x) = 2x3 - 1 (62) (√x-3)2 (65 48 (2√x-5)² (67 (3x-4)3 (66 الفصل 4 العلاقات والدوال العكسية والجذرية وزارة التعليم Ministry of Education 2024-1446