العمليات على الدوال - رياضيات2-2 - ثاني ثانوي
الفصل الرابع: العلاقات والدوال العكسية والجذرية
الفصل الخامس: العلاقات والدوال النسبية
الفصل السادس: المتتابعات والمتسلسلات
نشاط الفصل الرابع: العلاقات والدوال العكسية والجذرية
نشاط الفصل الخامس: العلاقات والدوال النسبية
4-1 العمليات على الدوال Operations on Functions www.icn.edu.sa لماذا؟ فيما سبق درست إجراء العمليات على تبين التمثيلات البيانية المجاورة الدخل السنوي كثيرات الحدود. والان لعائلة منذ عام 1430هـ ؛ حيث (f(x تعبر عن الدخل السنوي للزوج، و(x) تعبر عن الدخل السنوي للزوجة. الدخل السنوي للعائلة f(x) . أجد مجموع دالتين والفرق بينهما وحاصل يمكن التعبير عن إجمالي الدخل السنوي لتلك العائلة بالدالة (f(x) + (x 400+ 360- 320- 280 240 200+ 160 120 80+ 40 الدخل (بالاف الريالات) ضربهما وقسمتهما. أجد تركيب دالتين المفردات تركيب دالتين composition of functions 2 4 6 8 10 الأعوام منذ 1430هـ العمليات الحسابية : لقد أجريت العمليات الحسابية على كثيرات الحدود في الفصل السابق. ويمكنك إجراء عمليات الجمع والطرح، والضرب والقسمة على الدوال أيضًا. يمكنك الاعتماد على القواعد الآتية لإجراء العمليات الحسابية على الدوال: مفهوم أساسي العمليات على الدوال أضف إلى ويتك 12 12 العملية الجمع الطرح الضرب القسمة مثال f(x)=2x, g(x) = −x+5 2x+(-x+5)=x+5 2x-(-x+5)=3x-5 2x(-x+5)=-2x²+10x التعريف (f+g)(x) = f(x)+ g(x) (f-g)(x) = f(x)- g(x) (f⚫g)(x) = f(x) g(x) 2x -x+5 ,x #5 g(x) ()(x) = f(x), g(x) #0 مثال 1 جمع الدوال وطرحها إذا كان 1 + f(x) = x2 - 14, (x) = 2x، فأوجد كل دالة فيما يأتي: (f+g)(x) (a (f+g)(x) = f(x) + g(x) =(x24) + (2x+1) = x2 + 2x - 3 (f-g)(x) (b (f-g)(x) = f(x) = g(x) = (x2 - 4 - (2x + 1) = x2 - 2x - 5 تحقق من فهمك جمع دالتين عوض بسط طرح دالتين عوض بسط (f-g)(x) (1B f(x) = x²+5x-2, g(x)=3x-2 (f+g)(x) (1A الفصل 4 العلاقات والدوال العكسية والجذرية وزارة التعليم Ministry of Education 2024-1446

مراجعة المفردات التقاطع في المثال ،1 الدالتان (x) و (f(x لهما المجال نفسه، وهو مجموعة الأعداد الحقيقية. وكذلك الدالتان (x) + ) و (f(x) مجالاهما مجموعة الأعداد الحقيقية. يتكون مجال جميع الدوال الناتجة عن عمليات الجمع أو الطرح أو الضرب للدالتين (x) و (f(x من تقاطع مجاليهما. كما أن مجال الدالة الناتجة عن قسمة تقاطع مجموعتين هو هاتين الدالتين هو تقاطع مجاليهما أيضًا، مع استثناء القيم التي تجعل المقام يساوي صفرًا. مجموعة العناصر المشتركة بين هاتين المجموعتين، ويرمز له بالرمز . مثال 2 ضرب الدوال وقسمتها إذا كان 4 – f(x) = x2 + x + 12 (x) = 3x، فأوجد كلَّ دالة مما يأتي: (x) = f(x) (x) ضرب دالتين =(x2+7x+12)(3x-4) عوض خاصية التوزيع بسط (f⚫g)(x) (a 3x3 + 21x2 + 36x-4x² - 28x - 48 3x3+17x2+8x48 (b تنبيه ! قسمة دالتين بما أنه قد تم تعلم قسمة كثيرات الحدود في الفصل 3 فإنه سيكتفي عند إيجاد ناتج قسمة دالتين (في هذا الدرس) بكتابتهما في ((x) f(x) |(x)=- 8(x) = x2 + 7x + 12 3x-4 1x % 3 قسمة دالتين صورة دالة نسبية وتحديد مجالها من دون إجراء عملية القسمة. عوض بما أن م = x تجعل المقام 4 - 3x يساوي صفرا، فإن تـ تستثنى من ، مجال الدالة (x) (). تحقق من فهمك ()() (x) (2B f(x) = x2 - 7x + 2, g(x) = x + 4 (f⚫g)(x) (2A قراءة الرياضيات تركيب دالتين يرمز إلى تركيب الدالتين أ و 9 بالرمز .f[g(x)] ifog وتقرأ أ بعد و. تركيب دالتين : هي إحدى الطرائق التي تستعمل لدمج دالتين. وعند تركيب دالتين فإن قيم دالة منهما تستعمل الحساب قيم الدالة الأخرى. مفهوم أساسي تركيب دالتين التعبير اللفظي : إذا كانت f و 9 دالتين وكان مدى 9 مجموعة جزئية من مجال أ. فإنه يمكن إيجاد دالة التركيب f o g بالشكل : النموذج: أضف إلى تطوير مدى مدى و مجال f مجال f g [fog](x) = f[g(x)] g(x) f[g(x)] [fog](x) وزارة التعليم الدرس 1-4 العمليات على الدوال 13 2024-1446

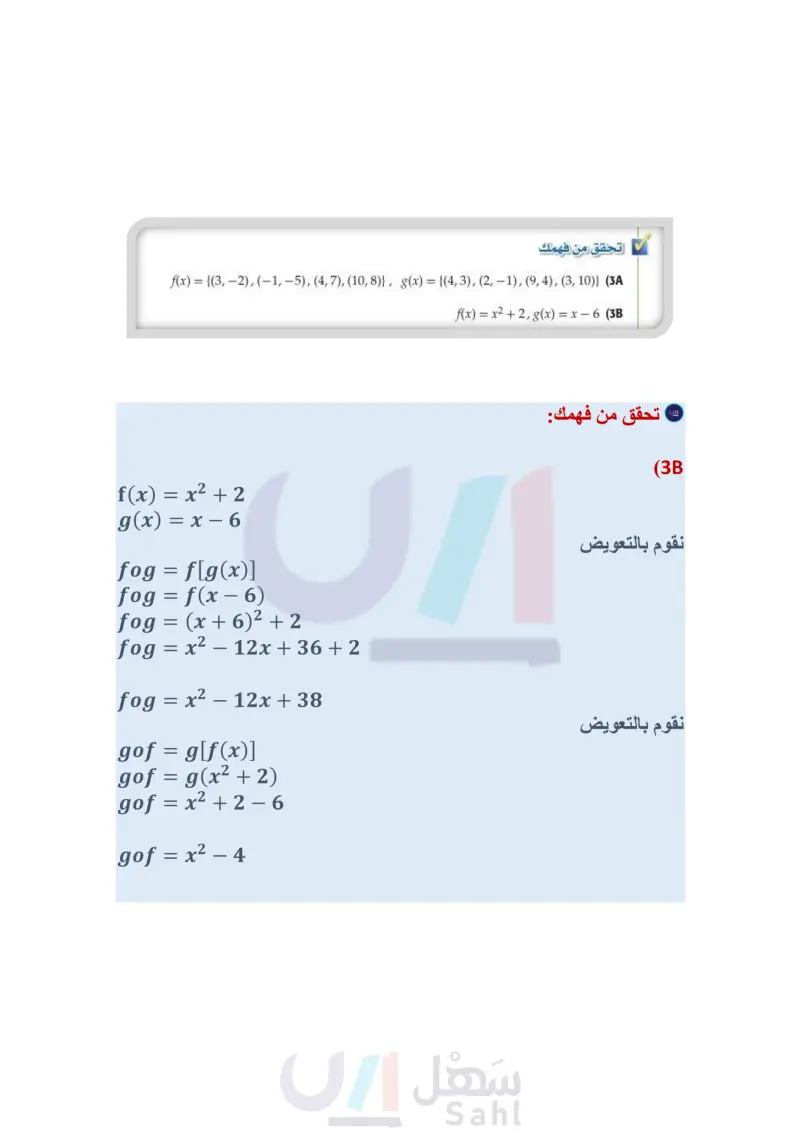
إرشادات للدراسة. التركيب كن حذرا من الخلط بين عملية تركيب دالتين [(f[g(x وعملية ضرب دالتين 14 .(f⋅ g)(x) يمكن أن يكون تركيب دالتين غير معرّف. فإذا كانت f و 8 دالتين، فإن (fox] يكون معرفًا فقط عند قيم x التي تجعل (x) عنصرًا في مجال الدالة .. وكذلك تكون الدالة (f(x معرفة فقط عند قيم x التي تجعل (f(x عنصرًا في مجال الدالة 8. تركيب دالتين مثال 3 أوجد (x), g of (x)، لكل زوج من الدوال الآتية، إذا كان ذلك ممكنا: f={(1, 8), (0, 13), (14, 9), (15, 11)}, g = {(8, 15), (5, 1), (10, 14), (9, 0)} (a لإيجاد fog، أوجد قيم (x) أولا، ثم استعملها كقيم من مجال الدالة لإيجاد [(f[(x 8(8)=15 g(5)=1 f [8(8)] = f(15) = 11 f[g(5)] = f(1) = 8 (10) = 14 8 (9)=0 fg(10)] = f(14) = 9 f[g(9)] = f(0) = 13 fog ((8, 11), (5, 8), (10, 9), (9, 13)} لإيجاد g of، أوجد قيم (f(x أولا ثم استعملها كقيم من مجال الدالة 8 ، لإيجاد [(f(x] 8 f(14)=9 g[f(14)] = g(9) = 0 f(15) = 11 g[f(15)] = g(11) (11) غير معرفة f(1) = 8 g[f(1)] = g(8) 15 f (0) = 13 g[f(0)] = g(13) (13) غير معرفة وبما أن 13 11 لا ينتميان لمجال الدالة 8 فإن الدالة g of غير معرفة عند 11 = x و 13 = x وبما أن .g[f(1)] = 15, g[f(14)] = 0 f(x)=2x-5, g(x) = 4x (b [fog](x)=f[g(x)] = f(4x) = 2(4x)-5 = 8x - 5 تحقق من فهمك .gof={(1, 15), (14,0)} تعريف تركيب دالتين عوض عوض بسط [gf](x) = g[f(x)] = g(2x-5) =4(2x-5) =8x-20 f(x) = {(3,-2), (-1,-5), (4, 7), (10,8)}, g(x) = {(4,3), (2, -1), (9,4), (3, 10)} (3A f(x) = x²+2, g(x) = x - 6 (3B لاحظ أنه في معظم الحالات تكون g of ؛ لذا فإن ترتيب الدالتين عند تركيبهما مهم. الفصل 4 العلاقات والدوال العكسية والجذرية وزارة التعليم Ministry of Education 2024-1446

التركيب
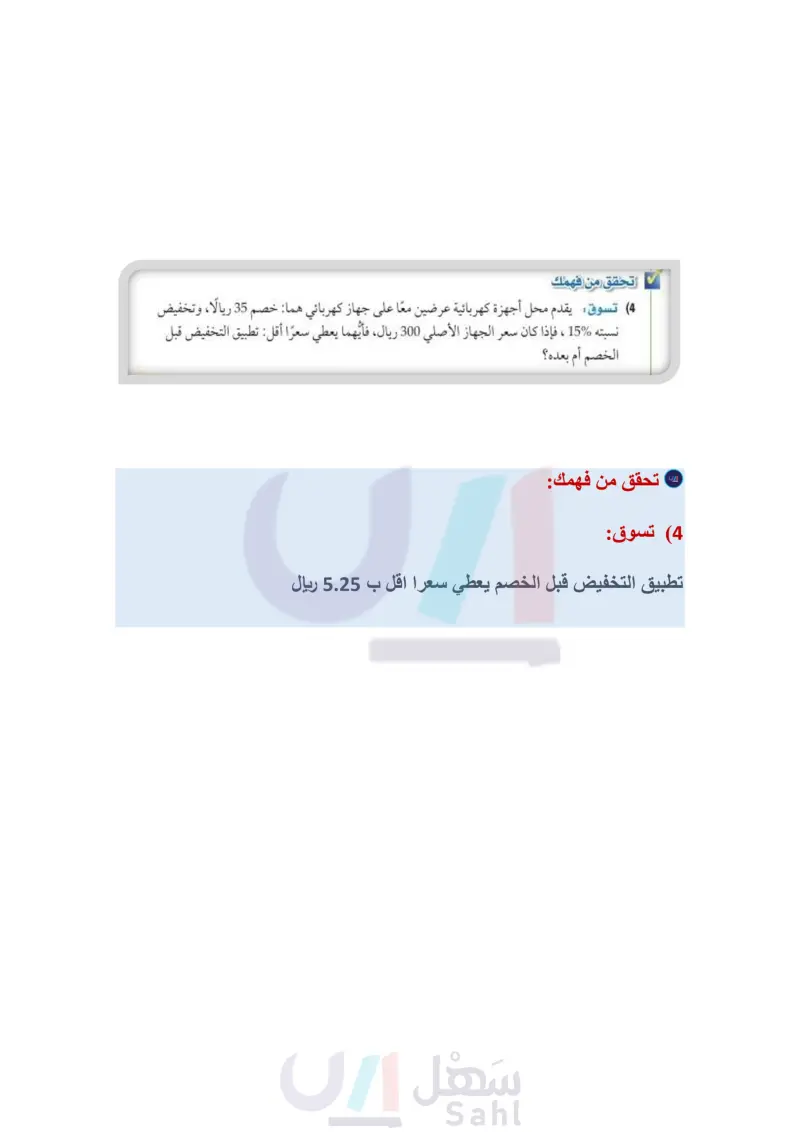
الربط مع الحياة في أعقاب الأزمة المالية مثال من واقع الحياة استعمال تركيب دالتين سيارات استعمل تركيب دالتين لحل المسألة الآتية: قدَّم معرض لبيع السيارات عرضًا بتخفيض %12% من قيمة كل سيارة جديدة. مضافًا إليه خصم مقداره 1500 ريال يقدمه وكيل شركة السيارات. فإذا أراد أحمد شراء سيارة جديدة سعرها 64500 ريال، فهل سيكون السعر النهائي للسيارة أقل إذا طبق التخفيض قبل الخصم أم بعده؟ افهم المعطيات . نسبة التخفيض من قيمة كل سيارة ،12، وقيمة الخصم 1500 ريال. • سعر السيارة التي يريد أحمد شراءها 64500 ريال. المطلوب: هل سيكون السعر النهائي للسيارة أقل إذا طبق التخفيض قبل الخصم أم بعده؟ العالمية عام 2009م، هبطت خطط افترض أن x تمثل السعر الأصلي للسيارة ، و (d(x تمثل السعر بعد التخفيض، و (r(x تمثل السعر بعد الخصم؛ إذن (rod] (x] تمثل السعر إذا طبق التخفيض قبل الخصم ، و (dor] (x] تمثل السعر إذا مبيعات كبرى شركات صناعة السيارات الأمريكية بصورة كبيرة بلغت 53 في أكبر طبق الخصم قبل التخفيض. حل اكتب معادلتين لدالتي التخفيض (x) ، والخصم (x) انخفاض لها منذ 42 عاما، مما يخفض المعرض 12% من السعر الأصلي للسيارة. فتكون دالة التخفيض اضطر هذه الشركات إلى خفض حجم إنتاجها بمقدار 400. d(x) = x - 0.12x = 0.88x يخصم الوكيل 1500 ريال من سعر كل سيارة جديدة؛ لذا فإن دالة الخصم هي: r(x)=x-1500 إذا طبق التخفيض قبل الخصم، فإن السعر النهائي للسيارة يُمثل بـ (64500)[r o d]. [rod](x) = r[d(x)] [rod](64500) = r[d(64500)] =r [0.88 (64500)] = r(56760) =56760 1500 = 55260 أما إذا طبق الخصم قبل التخفيض، فإن السعر النهائي للسيارة يُمثل بـ (64500)[d o r]. [dor](x) = d[r(x)] [dor](64500)=d[r(64500)] d(64500 1500) = d(63000) = 0.88 (63000) = 55440 وبما أن 55440 = 64500)[r o d](64500) = 55260, [d o r]. فإن السعر النهائي للسيارة سيكون أقل عندما يُطبق التخفيض قبل الخصم. تحقق تبدو الإجابة منطقية؛ لأن تخفيضا نسبته 12% سيتم تطبيقه على قيمة أكبر؛ لذا ستكون قيمة التخفيض أعلى. تحقق من فهمك (4) تسوق يقدم محل أجهزة كهربائية عرضين معًا على جهاز كهربائي هما خصم 35 ريالًا، وتخفيض نسبته 15 ، فإذا كان سعر | الجهاز الأصلي 300 ريال، فأيهما يعطي سعرا أقل: تطبيق التخفيض قبل الخصم أم بعده؟ وزارة التعليم الدرس 1-4 العمليات على الدوال 15 2024-1446

في أعقاب الأزمة المالية العالمية عام 2009 م ، هبطت مبيعات كبرى شركات صناعة السيارات الأمريكية بصورة كبيرة بلغت 53 % في أكبر انخفاض لها منذ 42 عاما.
أوجد () () () (۰) ,(x), ( - )x)( + ) للدالتين (f(x) ، (x في كل مما يأتي: المثالان 1 f(x) = x2 - 5 (2) g(x)=-x+8 f(x) = x + 2 (1 g(x)=3x-1 أوجد ۴۰۰ لكل زوج من الدوال الآتية، إذا كان ذلك ممكنا: مثال 3 f={(-5,4),(14,8), (12, 1), (0, -3)} (4) g={(-2,-4), (-3, 2), (-1, 4), (5,-6)} f={(2,5), (6,10), (12,9), (7,6)} (3 g={(9, 11), (6, 15), (10, 13), (5, 8)} أوجد (fox), go f(x] في كل مما يأتي، إذا كان ذلك ممكنا. f(x) = x + 4 (6 g(x) = x2 + 3x - 10 f(x)=-3x g(x)=5x-6 (5) (7) ادخار يقتطع ما نسبته 8% من راتب موظف للادخار. ويستطيع الموظف أن يختار بحيث يكون الاقتطاع مثال 4 قبل تسديده قسطا آخر قيمته 17.5% من الراتب، أو بعده. فإذا كان راتب الموظف قبل الاقتطاع وتسديد القسط 9500 ريال، فهل يكون ادّخاره أكثر إذا كان الاقتطاع قبل تسديد القسط أم بعده؟ وضّح إجابتك. وزارة التعليم Ministry of Education 2024-1446 تدرب وحل المسائل المثالان 12 أوجد () () () (۰) ,(x) ,( - (x) ( + ) للدالتين (f(x), (x في كل مما يأتي: f(x) = 3x2 - 4 (10 (x) = x2 - 8x + 4 f(x) = x2 (9 (x) = - x + 1 f(x) = x - 1 (8 g(x)=5x-2 11 رياضة المشي : يمشي راشد على ممر متحرك. فإذا كانت سرعته يُعبر عنها بالدالة: 4 - x) = 3x) وسرعة الممر المتحرك يعبر عنها بالدالة : 7 + x) = 4x) ، حيث x الزمن بالثواني. ما الدالة التي تعبر عن سرعته الكلية إذا كان يمشي في اتجاه سير الممر المتحرك؟ (6) ما الدالة التي تعبر عن سرعته الكلية إذا مشى في عكس اتجاه سير الممر المتحرك؟ مثال 3 أوجد foof لكل زوج من الدوال الآتية ، إذا كان ذلك ممكنا: f={(5, 13), (-4,-2), (-8, -11), (3, 1)) (13 g= {(−8, 2), (−4, 1), (3, -3), (5,7)} f={(-8,-4), (0, 4), (2, 6), (-6,-2)} (12 g={(4, 4), (-2, -1), (-4, 0), (6,-5)} f={(-1, 11), (2,-2), (5,-7), (4,-4)} (15 f= {(-4,-14), (0, -6), (-6, -18), (2,-2)} (14 8={(5, 4), (4,3), (-1,2), (2, 3)} g={(-6, 1), (-18, 13), (-14, 9), (-2, -3)} f(x) = 2x² (18 (x) = 8x2 + 3x أوجد (fox gfx في كل مما يأتي، إذا كان ذلك ممكنا: f(x)=4x-1 (17 (x) = x3 + 2 f(x) = 2x2 - x + 1 (16 g(x)=4x+3 الفصل 4 العلاقات والدوال العكسية والجذرية 16

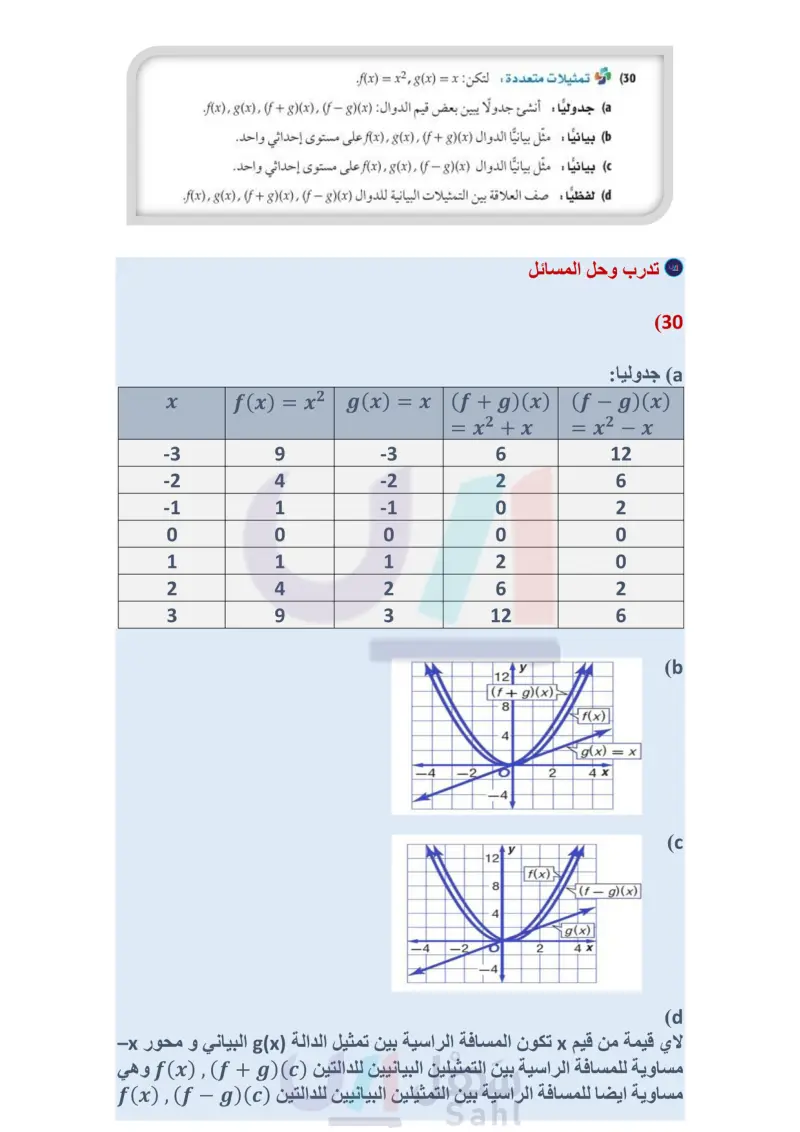
الربط مع الحياة مثال 4 الخاصية المميزة للشاشات (19) صناعة : ينتج مصنع نوعًا من الفناجين فإذا كان ثمن بيع x فنجان يُعبر عنه بالدالة: x) = 6.5x)، وتكلفة إنتاج x فنجان يُعبر عنها بالدالة : 1850 + x) = 0.75x). اكتب الدالة (x) التي تعبر عن ربح المصنع إذا باع x فنجان. أوجد ربح المصنع عند بيع 500 فنجان و 1000 فنجان و 5000 فنجان. (20) تسوق يرغب سامر في شراء تلفاز ذي شاشة مسطحة معروض للبيع بخصم نسبته %35 من السعر الأصلي. فإذا كان سعره الأصلي 2299 ريالا، ويضاف إليه 6.25 بدل ضمان بعد الخصم. a اكتب دالتين: الأولى تمثل سعر التلفاز بعد الخصم (p(x ، والثانية سعر التلفاز بعد إضافة بدل الضمان (f(x ) أي الدالتين الآتيتين يمثل سعر التلفاز النهائي: (pox، أم (to p](x]؟ وضح إجابتك. كم سيدفع سامر ثمنًا للتلفاز؟ إذا كان 3 - f(x) = x 2 + x - 12 x = x فأوجد كل دالة فيما يأتي، وحدد مجالها: (f-g)(x) (21 2(g⚫f)(x) (22 ()() (x) (23 المسطحة HDTV هي أن إذا كان 8 + f(x) = 5x, g (x) = 2x + 1, h(x) = x2 + 6x فأوجد قيمة كل مما يأتي: h[f(9)] (26 h[f(-5)] (25 8[f(a²-a)] (29 f[h(a + 4)] (28 g[h(3)] (24 flg(3a)] (27 30) تمثيلات متعددة لتكن : f(x) = x2 (x) = x a) جدوليًا أنشئ جدولا يبين بعض قيم الدوال : (f(x), (x), f ( x ) (x بيانيا مثل بيانيا الدوال ( x) ( f ) ( x) ، على مستوى إحداثي واحد. بيانيا : مثل بيانيا الدوال () () () () (f(x على مستوى إحداثي واحد. لفظيا : صف العلاقة بين التمثيلات البيانية للدوال (f(x), (x), f + (x) - (x (31) توظيف يمكن التعبير عن عدد الرجال والنساء الذين تم توظيفهم منذ عام 1434 هـ في مؤسسة ما بالمعادلتين الآتيتين: عدد الرجال: 6 + y = 7x عدد النساء : 5 + v = 5x حيث x تمثل عدد الأعوام منذ عام 1434هـ ، ولا تمثل عدد الموظفين. a اكتب دالة تمثل العدد الكلي للرجال والنساء الذين تم توظيفهم منذ عام 1434هـ. إذا كانت الدالة تمثل عدد الرجال الذين تم توظيفهم والدالة 8 تمثل عدد النساء اللاتي تم توظيفهن، فماذا تمثل الدالة (x) - )؟ إذا كان 1 + 2 - f(x) = x + 2, gx) = -4x + 3, hx = x2 فأوجد قيمة كل مما يأتي: ( (-6) (34 [(f+g) h](1) (33 (f.g.h)(3) (32 [ho (fog)](5) (37 [g (hof)](-4) (36 [fo (goh)](2) (35 وزارة التعليم الدرس 1-4 العمليات على الدوال 17 2024-1446 نسبة عرضها إلى ارتفاعها هي 16:9 ، فتوفر للمشاهد صورة أوضح.

اكتب دالتين: الأولى تمثل سعر التلفاز بعد الخصم p(x) ، والثانية سعر التلفاز بعد إضافة بدل الضمان t(x)

الخاصية المميزة للشاشات المسطحة HDTV هي أن نسبة عرضها إلى ارتفاعها هي 16:9 فتوفر للمشاهد صورة أوضح.
مسائل مهارات التفكير العليا (38) مسألة مفتوحة أوجد دالتين (f(x) (x) بحيث يكون 0 = (4)[8]. (39) اكتشف الخطأ : تقوم ريم والعنود بإيجاد الدالة (fox] ، حيث 18 + f(x) = x 2 + x - 8, 8(x) = x2 . من منهما إجابتها صحيحة؟ وضّح إجابتك. ريم العنود [fog](x)=f[g(x)] = (x²+8)²+2x-8 = x + 16X2 + 64 + 2 - 8 = x² + 16x²+2x+56 [fog (x) = fig(x)) = (x²+8)² + 2(x² +8)-8 = x + 16X2 + 64 + 2x 2 + 16 - 8 = x² + 18x² + 72 تدريب على اختبار 40) تحد : إذا كان f(x) = V , (x) = V6 فحدد مجال كل من الدالتين الآتيتين: [gog](x) (a ,g(x)= [fof](x) (b (41) تبرير: حدد ما إذا كانت كل من الجملتين الآتيتين صحيحة أحيانًا أو صحيحة دائمًا أو غير صحيحة أبدًا. وفسر إجابتك. يكون مجال الدالة [(f(x] هو نفس مجال الدالة f أو جزءًا منه. يكون مجال الدالة [(f(x] هو نفس مجال الدالة 8 أو جزءا منه. (42) اكتب وضّح لماذا نقوم بتركيب دالتين. وأعط مثالاً من واقع الحياة يمكنك حله باستعمال تركيب دالتين. وزارة التعليم Ministry of Education 2024-1446 44 إذا كان 5 + f(x) = 2x + 4, (x) = x2 فإن قيمة [(6)]f تساوي 38 A 43 B 86 C 261 D g(x) = x²+9x+21, h(x)=2(x+5)² LS 13 (43 فما الدالة المكافئة للدالة (x) - (x) (x) = - x2 - 11 - 29 A (x) = x2 + 11x + 29 B k(x) = x + 4 C (x) = x2 + x + 11 D مراجعة تراكمية اذكر العدد الممكن للأصفار الحقيقية الموجبة، والحقيقية السالبة، والتخيلية، لكلِّ من الدوال الآتية: (مهارة سابقة) f(x) = 2x4 - 23 + 5x2 + 3x - 9 (45 f(x) = 2x4 - 33 - 2x2 + 3 (46) in, 18in . ما المقدار الثابت من الطول الذي يجب إضافته إلى كلّ بعد من أبعاده، ليصبح حجمه (47) صندوق أبعاده 2in, 5985in3؟ (مهارة سابقة) حل كل معادلة فيما يأتي بالنسبة للمتغير المبين إزاء كل منها: (مهارة سابقة) (x+2)2 (y+5)² = 4,y (50 3x2 - 6xy + 1 = 4 ,y (49 5x 7y 12,x (48 الفصل 4 العلاقات والدوال العكسية والجذرية 18




 0
0 

 0
0 

 0
0