هياكل البيانات غير الخطية - الذكاء الاصطناعي - ثالث ثانوي
الجزء الأول
1. أساسيات الذكاء الاصطناعي
2. خوارزميات الذكاء الاصطناعي
3. معالجة اللغات الطبيعية
الجزء الثاني
4. التعرف على الصور
5. خوارزميات التحسين واتخاذ القرار
6. الذكاء الاصطناعي والمجتمع
الدرس الثالث هياكل البيانات غير الخطية رابط الدرس الرقمي www.ien.edu.sa في الدرس السابق تعلّمت بعض هياكل البيانات الخطية، وفيها كل عنصر يتبع العنصر السابق له بطريقة خطية. هل يمكنك التفكير في حالة لا تسير فيها الأشياء بتسلسل خطي؟ على سبيل المثال، هل يمكن لعنصر واحد أن يتبعه أكثر من عنصر ؟ هياكل البيانات غير الخطية Non-Linear Data Structures هي نوع من هياكل البيانات يتميز بإمكانية ربط عنصر بأكثر من عنصر واحد في الوقت نفسه. ومن الأمثلة التوضيحية على هياكل البيانات غير الخطيَّة: الأشجار ومُخطَّطات البيانات الشكل 1.33 يوضّح هياكل البيانات الخطية وهياكل البيانات غير الخطية. هياكل البيانات الخطية HI هياكل البيانات غير الخطية شكل 1.33: الرسم التوضيحي لهياكل البيانات الخطية وغير الخطية جدول 1.9 الفرق بين هياكل البيانات الخطية وغير الخطية هياكل البيانات الخطية هياكل البيانات غير الخطية تُرتب عناصر البيانات في ترتيب خطي يرتبط فيه يمكن ربط عناصر البيانات بالعديد من العناصر الأخرى. كل عنصر بالعنصرين السابق والتالي له. تُستعرض عناصر البيانات في مسار واحد. سهل التنفيذ. لا تُستعرض عناصر البيانات في مسار واحد. معقد التنفيذ. 53 وزارة التعليم Ministry of Education 2024-1446

54 عقدة و الأشجار Trees الأشجار هي نوع من هياكل البيانات غير الخطية، وتتكون الشجرة من مجموعة من العقد المرتبة في ترتيب هرمي. ترتبط كل عقدة بواحدة أو أكثر من العقد، وترتبط العقد مع الحواف في نموذج علاقة يربط بين الأصل (Parent) والفرع (Child) . تُستخدم الأشجار في العديد من مجالات علوم الحاسب، بما في ذلك أنظمة التشغيل، والرسوميات، وأنظمة قواعد البيانات، والألعاب، والذكاء الاصطناعي، وشبكات الحاسب. مصطلحات تقنية الشجرة المستخدمة في هيكل بيانات الشجرة Tree Terminology Used in the Tree Data Structure حافة شكل 1.34 العلاقات في الشجرة الجذر (Root): العُقدة الأولى والوحيدة في الشجرة التي ليس لها أصل وتأتي في المستوى الأول من الشجرة، مثل: العقدة A في الشكل 1.35. الفرع (Child): العقدة المرتبطة مباشرةً بعقدة في المستوى الأعلى، مثل: العقدة H هي فرع العقدة ،D ، والعُقدتان B وC هما فرعا العقدة A. الأصل (Parent): العقدة التي لها فَرع أو أكثر في المستوى الأقل، مثل: العقدة B الورقة (Leaf): العقدة التي ليس لها أي عقدة فرعية، مثل: الورقة F. و هي أصل العُقدتين D وE. • الأشقاء (Siblings) كل العقد الفرعية التي تنبثق من الأصل نفسه، مثل: العُقدتان D وE شقيقتان. • الحواف (Edges): الروابط التي تصل بين العقد والشجرة. الشجرة الفرعية (Sub-Tree) الشجيرات التي توجد داخل الشجرة الأكبر حجمًا ، مثل: الشجرة التي بها العقدة الأصل والعقدتان H وا هما الفرعان. D هي المستوى الأول المستوى الثاني المستوى الثالث G C الورقة المستوى الرابع A الحواف الأشقاء الجذر B D E F ل العقدة شكل 1.35 هيكل بيانات الشجرة الشجرة الفرعية الفرع الشجرة (Tree) : الشجرة هي نوع من هياكل البيانات غير الخطية، وتتكون من مجموعة من العقد المرتبة في ترتيب هرمي. العقدة الأصل الحافة (Edge) : H الحافة تصل بين عقد هيكل بيانات الشجرة. قد يكون لديك شجرة بسيطة تتكون من عقدة واحدة تكون هذه العقدة في الوقت نفسه جذر هذه الشجرة البسيطة؛ لأنها ليس لها أصل. وزارة التعليم Ministry of Education 2024-1446

55 قد تكون العقدة فرعًا وأصلا الجذر في الوقت نفسه : فرع للعقدة السابقة وأصل للعقدة التالية. العقدة الأصل الفقاريات الحيوانات وفيما يلي مثال على هيكل بيانات الشجرة اللافقاريات العنكبوتيات الحشرات الثدييات الأسماك الطيور العقدة الفرع وزارة التعليم Ministry of Education 2024-1446 الجمل الحصان النمر الأشقاء شكل 1.36 مثال على هيكل بيانات الشجرة خصائص هيكل بيانات الشجرة Tree Data Structure Features يُستخدم لتمثيل المخطّط الهرمي. يتميّز بالمرونة، فمن السهل إضافة عنصر من الشجرة أو حذفه. سهولة البحث عن العناصر فيه. يعكس العلاقات الهيكلية بين البيانات. مثال تنظيم الملفات في نظام التشغيل هو مثال عملي على الشجرة. كما يتضح في الشكل ،1.37، يوجد داخل مجلد Documents (المستندات) مجلد آخر اسمه Phon Project مشروعات البايثون يحتوي على ملفين آخرين. This PC = | Python Projects File Home Share This PC 3D Objects Desktop Documents Music Downloads Pictures 3D Objects Desktop Documents Alice Alice Python Projects HelloWorld.py infinite.py شكل :1.37 تنظيم الملفات في نظام التشغيل View الورقة > This PC > Documents > Python Projects Python Projects Downloads Music Pictures Name HelloWorld infinite

d b هيكل بيانات الشجرة في لغة البايثون Tree Data Structure in Python لا تُوفِر لغة البايثون نوعًا محددًا مسبقًا من البيانات لهيكل بيانات الشجرة. ومع ذلك، تُصمَّم الأشجار من القوائم والقواميس بسهولة. يوضّح الشكل 1.38 تطبيقًا بسيطًا للشجرة باستخدام القاموس. f C a e في هذا المثال، ستنشئ شجرة باستخدام قاموس البايثون. ستمثل عقد شكل 1.38 شجرة قاموس البايثون الشجرة مفاتيح القاموس ، وستكون القيمة المقابلة لكل مفتاح هي قائمة تحتوي على العقد المتصلة بحافة مباشرة من هذه العقدة. myTree = { "a": ["b", "c"], #node "b": ["d", "e"], "c": [None, "f"], "d": [None, None], } "e": [None, None], "f": [None, None], print(myTree) {'a': ['b', 'c'], 'b': ['d', 'e'], 'c': [None, 'f'], 'd': [None, None], 'e': [None, None], 'f': [None, None]} Data Structures Linear Non-linear Stack Queue Tree Graph في المثال التالي ستنشئ شجرة مثل تلك الموضحة في الشكل 1.39 : الأصل الفرع myTree = {"Data Structures":["Linear", "Non-linear"], "Linear":["Stack", "Queue", "Linked List"], "Non-linear":["Tree", "Graph"]} for parent in myTree: print(parent, "has",len(myTree[parent]), "nodes" ) for children in myTree[parent]: print(" ",children) Data structures has 2 nodes Linear Non-linear Linear has 3 nodes Stack Queue Linked List Non-linear has 2 nodes Linked List Tree Graph شكل 1.39 شجرة هياكل البيانات. وزارة التعليم Ministry of Education 2024-1446 56

57 وزارة التعليم Ministry of Education 2024-1446 الشجرة الثنائية Binary Tree الشجرة الثنائية هي نوع خاص من الأشجار، يكون لكلّ عُقدة فيها فرعان على الأكثر؛ الفرع الأيمن والفرع الأيسر. الشكل 1.40 يعرض مثالاً يوضّح الشجرة والشجرة الثنائية. b d e h i 20 a الشجرة الثنائية f g 60 CD k a b C d f مه g h i j الشجرة | m شكل 1.40: الشجرة والشجرة الثنائية جدول 1.10: أنواع هياكل بيانات الشجرة الثنائية النوع الشجرة الثنائية التامة (Full Binary Tree) الوصف يكون لكلّ عُقدة إما 0 أو 2 من الفروع ( Children) بخلاف الأوراق (Leaves). الشجرة الثنائية الكاملة يكون كلّ مستوى من مستويات الشجرة ممتلئًا (Complete Binary Tree) بالكامل، ربما باستثناء المستوى الأخير، حيث تكون كل العقد فيه مملوءة من اليسار إلى اليمين. الفرع الأيمن الفرع الأيسر رسم توضيحي للهيكل 1 2 3 4 0 1 2 3 4 5 1 2 3 4 5 6 الشجرة الثنائية المثالية يكون لكل العقد الداخلية فرعان وتكون كل الأوراق عند المستوى نفسه. (Perfect Binary Tree ) أمثلة على تطبيقات هياكل بيانات الشجرة : Examples of Applications of Tree Data Structures • تخزين البيانات الهرمية مثل هياكل المجلدات. • تعريف البيانات في لغة ترميز النص التشعبي (HTML). تنفيذ الفهرسة في قواعد البيانات.

58 شجرة القرار Decision Tree هل تقدم الجامعة المقرر لا نعم تجاهل هل درجاتي تلبي شروط القبول؟ نعم عبارة القرار if a else b هي واحدة من العبارات الأكثر استخدامًا في لغة البايثون. الدراسي الذي أريده؟ ومن خلال تداخل وتجميع هذه العبارات، يمكنك تصميم شجرة القرار. تُستخدم أشجار القرار في الذكاء الاصطناعي من خلال إحدى تقنيات تعلم الآلة وتُعرف باسم تعلّم شجرة القرار Decision. Tree Learning) العقد الأخيرة في هذه التقنية تُسمّى أيضًا الأوراق، وتحتوي على الحلول المحتملة للمشكلة. كل عقدة باستثناء الأوراق ترتبط بحالة منطقية يتفرع منها احتمالا الإجابة بنعم أولا. أشجار القرار تُعد سهلة الفهم ، والاستخدام، والتصوير، ويسهل التحقق منها . على سبيل المثال، الشكل 1.41 يوضّح شجرة القرار التي تُحدد ما إذا كنت ستتقدم بطلب الالتحاق بجامعة مُحدَّدة أم لا بناءً على معيارين: المقررات الدراسية التي تُدرَّس في الجامعة، واستيفاء متطلبات شكل :1.41 مثال على شجرة القرار القبول. المخطّطات Graphs و تجاهل لا تطبيق السمة الأكثر أهمية لهياكل البيانات غير الخطيَّة هي أنّ البيانات الخاصة بها لا تتبع أي نوع من أنواع التسلسل، وذلك على خلاف المصفوفات والقوائم المترابطة، كما يمكن الخطَّط (Graph ) : ربط عناصرها بأكثر من عنصر وحيد الشجرة الجذرية (Rooted Tree) تبدأ المُخطَّط. هو هيكل البيانات المكون بعقدة جذرية يمكن ربطها بالعقد الأخرى. تتبع الأشجار قواعد محددة: وهي أن تكون من مجموعة من العقد ومجموعة عقد الشجرة متصلة، وأن تكون الشجرة خالية من الحلقات ( Loops) والحلقات الذاتية من الخطوط التي تصل بين جميع (Self Loops) ، كما أن لبعض أنواع الأشجار قواعدها الخاصة (جدول 1.10) ، مثلما العقد، أو بعضها . في حالة الأشجار الثنائية. ولكن ماذا سيحدث إذا لم تَتَّبع قواعد الأشجار؟ في هذه الحالة أنت لا تتحدث عن الأشجار ، بل عن نوع جديد من هياكل البيانات المتغيرة التي تُسمى المخطّطات. في الحقيقة، الأشجار هي نوع من المُخطَّطات حيث أن المُخطَّط كل الأشجار مُخطَّطات، ولكن ليست الشكل العام لهيكل البيانات، بمعنى أن كل هياكل البيانات السابقة يمكن اعتبارها حالات خاصة من المخطّطات. الشكل 1.42 يعرض مُخطَّطًا به ست عُقد وعشر حواف. جدول :1.11 الفرق بين الأشجار والمخططات الأشجار الخطَّطات تشكّل العقد المتّصلة فيها نموذجًا تشكّل العقد المتصلة فيها هرميًّا. نموذجًا شبكيًّا. في الأشجار الجذرية توجد عُقدة لا توجد فيها عُقدة فريدة فريدة تُسمى الجذر. و أو جذرية. ترتبط العقد في صورة علاقة بين لا تنطبق علاقة الأصل الأصل والفرع. تتميز ببساطة التركيب. لا يُسمح فيها بالحلقات. و والفرع بين العقد. تركيب المخطَّطات أكثر تعقيدا. قد تحتوي على الحلقات 3 6 كل المخططات أشجارا. 2 1 5 4 شكل 1.42: مثال على مُخطَّط به ست عُقد وعشر . وزارة التعليم Ministry of Education 2024-1446

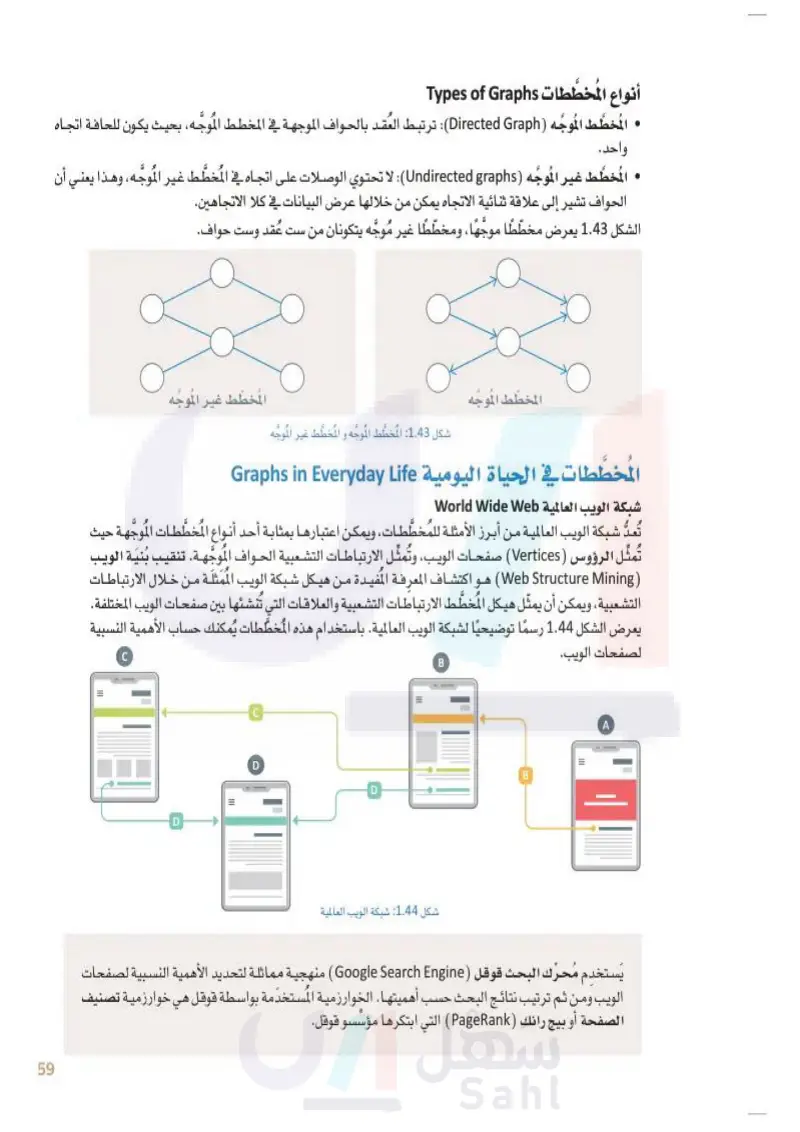
59 أنواع المخططات Types of Graphs • المخطط الموجه Directed Graph): ترتبط العقد بالحواف الموجهة في المخطّط الموجه، بحيث يكون للحافة اتجاه واحد. ، المُخطَّط غير الموجه Undirected graphs : لا تحتوي الوصلات على اتجاه في المُخطَّط غير الموجه، وهذا يعني أن الحواف تشير إلى علاقة ثنائية الاتجاه يمكن من خلالها عرض البيانات في كلا الاتجاهين. الشكل 1.43 يعرض مُخطَّطًا موجهًا ، ومُخطَّطًا غير مُوجَّه يتكونان من ست عقد وست حواف. وزارة التعليم Ministry of Education 2024-1446 المخطط الموجه شكل 1.43: المُخطَّط الموجه والمُخطَّط غير الموجه الخطَّط غير الموجه المخطَّطات في الحياة اليومية Graphs in Everyday Life شبكة الويب العالمية World Wide Web تُعدُّ شبكة الويب العالمية من أبرز الأمثلة للمخطَّطات، ويمكن اعتبارها بمثابة أحد أنواع المخططات الموجهة حيث تُمثَّل الرؤوس (Vertices) صفحات الويب، وتُمثَّل الارتباطات التشعبية الحواف الموجّهة. تنقيب بُنية الويب (Web Structure Mining هو اكتشاف المعرفة المفيدة من هيكل شبكة الويب الممثلة من خلال الارتباطات التشعبية، ويمكن أن يمثل هيكل المُخطَّط الارتباطات التشعبية والعلاقات التى تنشئها بين صفحات الويب المختلفة. يعرض الشكل 1.44 رسما توضيحيًا لشبكة الويب العالمية. باستخدام هذه المُخطَّطات يُمكنك حساب الأهمية النسبية لصفحات الويب. B C D C D D = شكل 1.44 شبكة الويب العالمية B A يَستخدم مُحرك البحث قوقل (Google Search Engine ) منهجية مماثلة لتحديد الأهمية النسبية لصفحات الويب ومن ثم ترتيب نتائج البحث حسب أهميتها. الخوارزمية المستخدمة بواسطة قوقل هي خوارزمية تصنيف الصفحة أو بيج رانك (PageRank) التي ابتكرها مؤسسو قوقل.

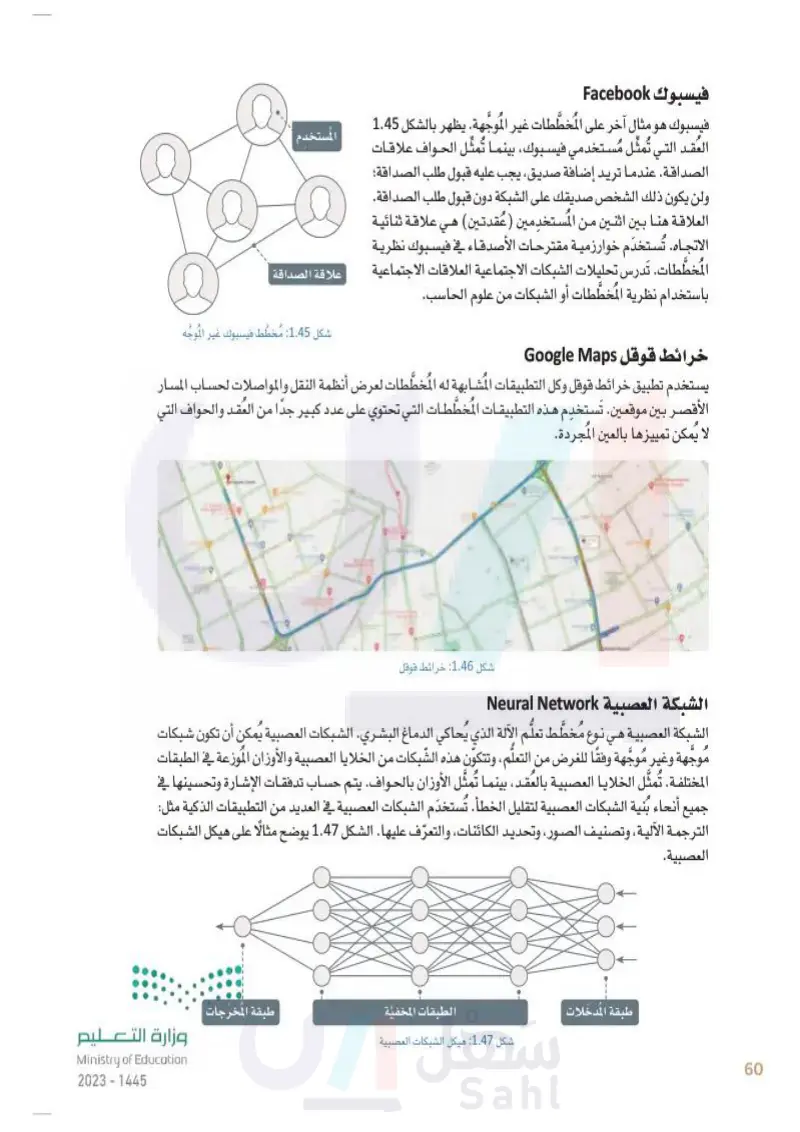
وزارة التعليم Ministry of Education 2024-1446 فيسبوك Facebook المستخدم فيسبوك هو مثال آخر على المُخطَّطات غير الموجهة. يظهر بالشكل 1.45 العقد التي تُمثّل مُستخدمي فيسبوك، بينما تمثل الحواف علاقات الصداقة. عندما تريد إضافة صديق، يجب عليه قبول طلب الصداقة؛ ولن يكون ذلك الشخص صديقك على الشبكة دون قبول طلب الصداقة. العلاقة هنا بين اثنين من المستخدمين ( عُقدتين) هي علاقة ثنائية الاتجاه. تُستخدم خوارزمية مقترحات الأصدقاء في فيسبوك نظرية المخطّطات. تدرس تحليلات الشبكات الاجتماعية العلاقات الاجتماعية علاقة الصداقة باستخدام نظرية المخطّطات أو الشبكات من علوم الحاسب. خرائط قوقل Google Maps شكل 1.45: مُخطَّط فيسبوك غير الموجه يستخدم تطبيق خرائط قوقل وكل التطبيقات المشابهة له المُخطَّطات لعرض أنظمة النقل والمواصلات لحساب المسار الأقصر بين موقعين. تستخدم هذه التطبيقات المخطّطات التي تحتوي على عدد كبير جدًا من العقد والحواف التي لا يمكن تمييزها بالعين المجردة. Olaya Kingdom Centre Dr. Sulaiman Al Ta Olaya Medical Complex shawarma house bib Nevermind Jarir Bookstore مكتبة جريرات Najd Villag Gentria Mal Panorama Mall UMM AL بانوراما مول AL MATHAR ASH SHAMALI Tahlah St HAMAM AL SHARQI MARBLE Tahliah St ocalizer Mall لوكالين Al Faisaliah Hotel Haraj Computer Smart Shopping الدورة Manna-Noura AS SULIMANIYAH Prince Sultan Military Medical City Cebu Bakr Airaz Children's Specialized Hospital King Fahad.. 522 الاطفال مدينة الأمير ستيك ALMUTA HOTEL RADH مدق المطلق The View Mally Security Forces Hospital Main Building AD DHUBBAT قوى الأمن KING ABDUL AZIZ AZ ZAHRA EatmatratZah Rivadh 700 Shurfa مطعم الشرفة Sulalat Coffee Ministry of the National Guard دی از در الحرس الوطني NewMax 21 min TOP UP | Rabwah 17.2 km AR RAYYAN Riyadh Care Hospital Care Hooping AbiArArahiah 20 min 18.3 km Yubah Bake Al Nahda Park Al Othaim Malle JARIR AIMajd mall Muhammad Ibn All Qassim Park OAl Rajhi Mosque Prince Mohammed Bin Abdulaziz Hospital المشفى الأمير له بن عبد العزيز AR RAWABI AISadhan Supermarket Rawabi برق العليا للوازم الرحلات Danube اسواق السلمان الروابي ة الخليج 3 ق بودل الفيحاء AIR الشبكة العصبية Neural Network شكل 1.46: خرائط قوقل الشبكة العصبية هي نوع مُخطّط تعلُّم الآلة الذي يُحاكي الدماغ البشري. الشبكات العصبية يمكن أن تكون شبكات مُوجّهة أو غير مُوجَّهة وفقًا للغرض من التعلم، وتتكوّن هذه الشبكات من الخلايا العصبية والأوزان الموزعة في الطبقات المختلفة. تُمثَّل الخلايا العصبية بالعقد، بينما تُمثَّل الأوزان بالحواف. يتم حساب تدفقات الإشارة وتحسينها في أنحاء بنية الشبكات العصبية لتقليل الخطأ. تُستخدم الشبكات العصبية في العديد من التطبيقات الذكية مثل: الترجمة الآلية، وتصنيف الصور، وتحديد الكائنات، والتعرّف عليها . الشكل 1.47 يوضّح مثالا على هيكل الشبكات جميع العصبية. طبقة المدخلات الطبقات المخفية طبقة المخرجات | شكل :1.47 هيكل الشبكات العصبية 60

61 وزارة التعليم Ministry of Education 2024-1446 d b المخطط a شكل 1.48 مثال على المُخطَّطات في لغة البايثون Graphs in Python لا تُوفِر لغة البايثون نوعًا محددًا مسبقًا من البيانات للأشجار، كما أنّها لا تُوفِر نوعًا محددًا مسبقا من البيانات للمُخطَّطات، تذكر أن الأشجار هي نوع خاص من المُخطَّطات) . ومع ذلك، يُمكن بناء المخطّطات باستخدام القوائم والقواميس. في المثال التالي، ستقوم بتنفيذ التالي 1. إنشاء مُخطَّط مُوجّه مثل الموضح بالشكل 1.48. 2. إنشاء دالة لإضافة عُقدة إلى المُخطَّط. 3. إنشاء كائن يحتوي على كل مسارات المخطّط. e myGraph = { "a" : ["b","c"], "b" : ["c", "d"], "c" : ["d", "e"], "d" : [], "e" : [], } print(myGraph) {'a': ['b', 'c'], 'b': ['c', 'd'], 'c': ['d', 'e'], 'd': [], 'e': []} وسيتولى البرنامج الرئيس: 1. إنشاء المخطط. 2. طباعة المُخطَّط. 3. استدعاء دالة الإضافة. 4. طباعة كل مسارات المخطّط. ستَستخدم القاموس الذي تُمثَّل مفاتيحه العُقد بالمخطّط. تكون القيمة المقابلة لكل مفتاح هي قائمة تحتوي على العقد المتصلة بحافة مباشرة من هذه العقدة. #function for adding an edge to a graph def addEdge(graph, u, v): graph[u].append(v) #function for generating the edges of a graph def generate_edges(graph): edges = [] # for each node in graph for node in graph:

وزارة التعليم Ministry of Education 2024-1446 # for each neighbouring node of a single node for neighbour in graph[node]: # if edge exists then append to the list edges.append((node, neighbour)) return edges #main program # initialisation of graph as dictionary myGraph = {"a" : ["b","c"], } "b" : ["c", "d"], "c" ["d", "e"], "d" : [], "e" : [], # print the graph contents print("The graph contents") print(generate_edges (myGraph)) # add more edges to the graph addEdge (myGraph, 'a', 'e') addEdge (myGraph,'c', 'f') # print the graph after adding new edges print("The new graph after adding new edges") print(generate_edges (myGraph)) The graph contents [('a', 'b'), ('a', 'c'), ('b', 'c'), ('b', 'd'), ('c', 'd'), ('c', 'e')] The new graph after adding new edges. [('a', 'b'), ('a', 'c'), ('a', 'e'), ('b', 'c'), ('b', 'd'), ('c', 'd'), ('c', 'e'), ('c', 'f')] 62

1 تمرينات حدد الجملة الصحيحة والجملة الخاطئة فيما يلي: 1. يمكن ربط العنصر في هياكل البيانات غير الخطيَّة بأكثر من عنصر واحد. لک 2 . تنفيذ هياكل البيانات الخطيَّة يكون أكثر تعقيدًا من تنفيذ هياكل البيانات غير الخطية. 3 الأوراق في تعلُّم شجرة القرار تحتوي على حلول المشكلة. .4. تحسب خوارزمية قوقل تصنيف الصفحة ( PageRank) الأهمية النسبية لصفحة ويب على شبكة الويب العالمية. 5. الشبكات العصبية هي نوع المُخطَّطات المستخدم لتصوير المشكلات الأخرى. 2 وضّح الاختلافات بين الأشجار والمخططات. الأشجار 3 صف كيف تُستخدَم خوارزميات المخطَّطات في التطبيقات التجارية. المخططات صحيحة خاطئة 63 وزارة التعليم Ministry of Education 2024-1446

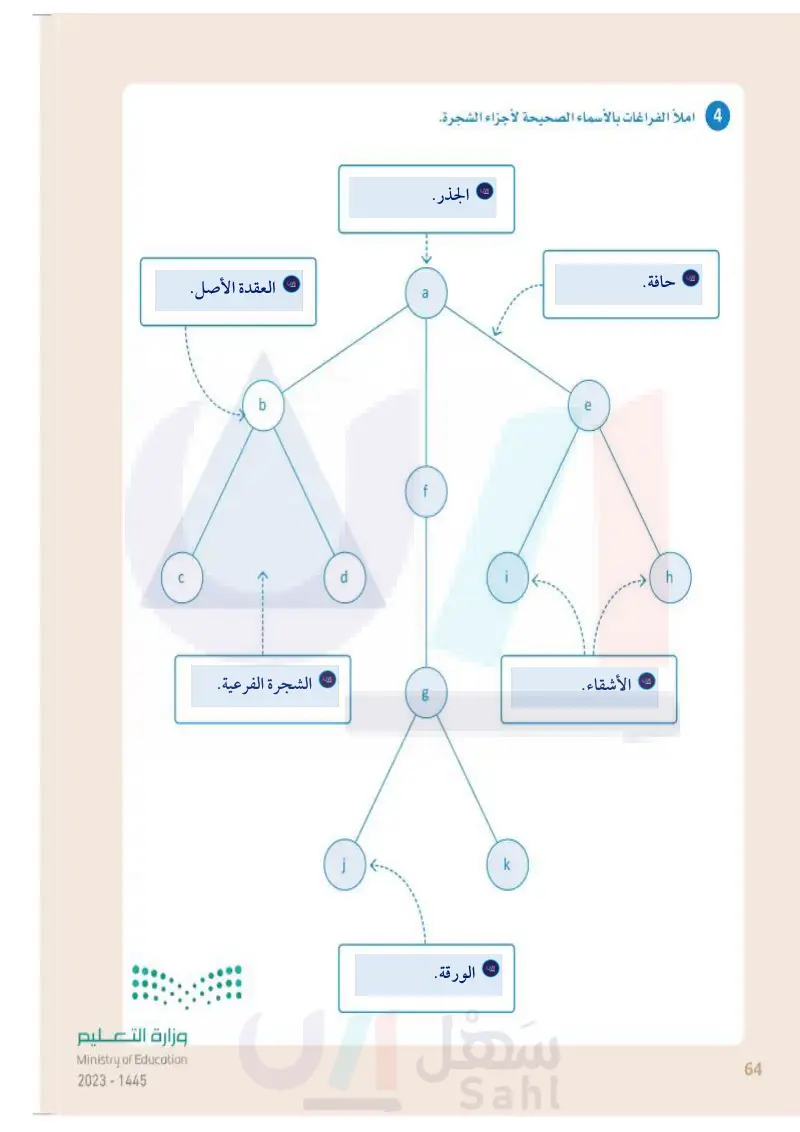
وزارة التعليم Ministry of Education 2024-1446 b C d 60 g 1 a 4 املأ الفراغات بالأسماء الصحيحة لأجزاء الشجرة. k e h 64

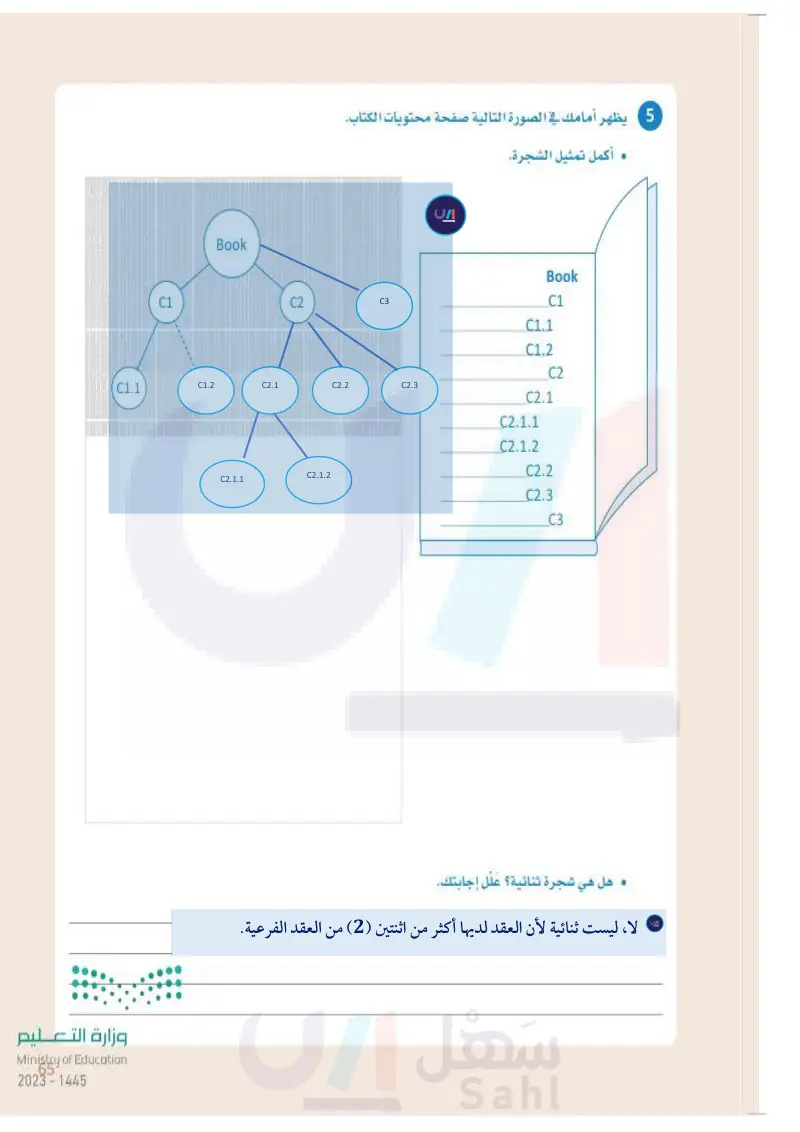
65 وزارة التعليم Ministry of Education 2024-1446 C1.1 C1 1 T Book يظهر أمامك في الصورة التالية صفحة محتويات الكتاب. 5 يظهر • أكمل تمثيل الشجرة. Book C2 C1 C1.1 C1.2 C2 C2.1 C2.1.1 C2.1.2 C2.2 C2.3 C3 • هل هي شجرة ثنائية ؟ عَلَّل إجابتك.

وزارة التعليم Ministry of Education 2024-1446 6 ارسم الشجرة الناتجة عن المعطيات التالية العقدة A لها فرعان B و C . العُقدتان D و E لهما الأصل نفسه وهو العُقدة B. وE العُقدتان F و G شقيقتان، ولهما الأصل نفسه العقدة C. العقدة H لها عُقدتان فَرعيتان اول ولها عُقدة أصل .F . ما نوع الشجرة المرسومة في الأعلى؟ 66

67 باستخدام القاموس في لغة البايثون اكتب البرنامج المناسب لتمثيل هذه الشجرة، ثم أضف العُقدة الأصل والعقد الفرعية. وزارة التعليم Ministry of Education 2024-1446




 0
0