الأعداد المركبة - رياضيات2-1 - ثاني ثانوي

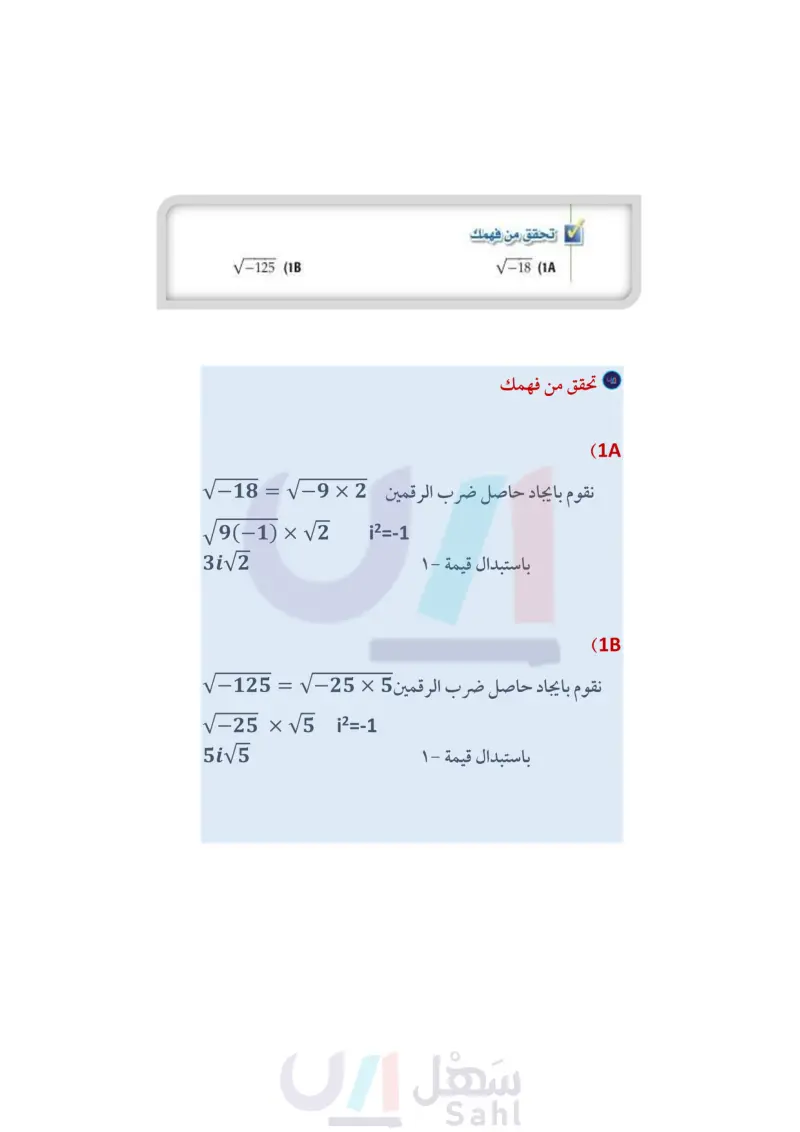
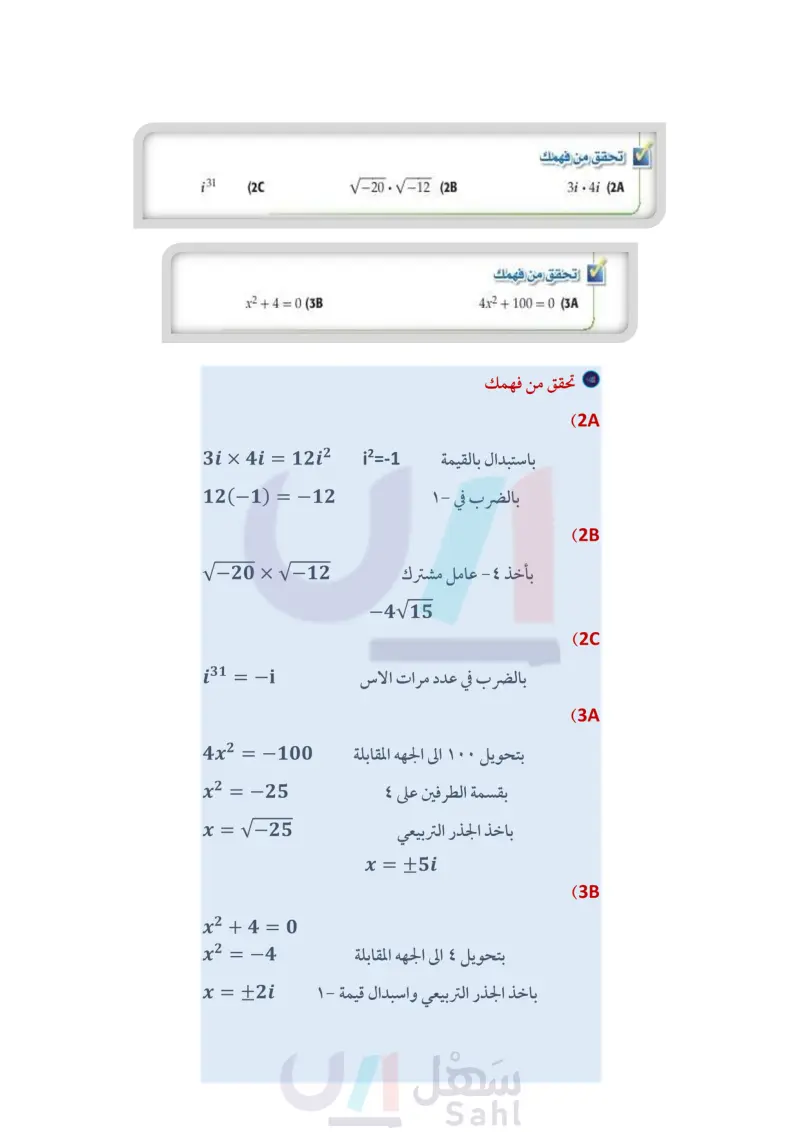
رابط الدرس الرقمي www.ien.edu.sa الأعداد المركبة Complex Numbers 3-1 فيما سبق : درست تبسيط الجذور التربيعية. (مهارة سابقة) والآن : - أُجري العمليات على الأعداد التخيلية البحتة ه أُجري العمليات على الأعداد المركبة المفردات الوحدة التخيلية imaginary unit العدد التخيلي البحت لماذا ؟ بالنظر إلى الشكل المجاور، تلاحظ أن التمثيل البياني للمعادلة 4 + y = x2 + 2x لا يقطع المحور x ، لذا ليس للمعادلة جذور حقيقية، ذلك أنه ليس للمعادلة حلول ؟ فهل يعني للتأكد من ذلك استعمل الآلة الحاسبة بالضغط على مفتاح non، ومنها اختر 1 اضغط ثم اختر :إضافة تطبيق الحاسبة ثم اذ مستند جدید العمليات الجبرية :3 أدوات كثيرات الحدود menu الجذور الحقيقية لكثيرات الحدود enter واختر منها فيظهر على الشاشة 10 1.1 1.1 烤 107y -106 f1(x)=x2+2x+4 0.5 [-6, 10] scl: 0.5 by [-2, 10] scl: 0.5 冈色 -*106b poly Roots (x²+2x+4) خطأ : لم يتم تعريف المتغير" أنه لا توجد حلول حقيقية للمعادلة، ولكن هناك حلول ثم أدخل 4 + x2 + 2x واضغط enter كلمة خطأ، وهذا يعني تخيلية. 1/99 الأعداد التخيلية البحتة قادت المعادلات كالمعادلة السابقة الرياضيين إلى تعريف الأعداد التخيلية، ووحدتها التخيلية i ، حيث تعرف الوحدة التخيلية i على أنها الجذر التربيعي الموجب للعدد 1- ، وبعبارة أخرى فإن 1-i = V ، وهذا يعني أن 1 = 2 i - والأعداد في الصورة 3 ,2 ,6i، تسمى أعدادًا تخيلية بحتة، وهي جذور تربيعية لأعداد حقيقية سالبة. لأي عدد حقيقي موجب مثل ، فإن b2 = V2. V-1 = bi- مثال 1 بسط كلا مما يأتي : b الجذور التربيعية للأعداد السالبة /−216 = √√−1·6².6 = = V-10762 =i.6.√6 = 6i√6 = = √√−216 (b -27 = = √√−1·3².3 V6 = V-1.32.3 =i.3.√√3 =3i√√3 √-125 (1B √-27 (a تحقق من فهمك √-18 (1A تُحقق الأعداد التخيلية البحتة كلَّا من الخاصيتين (التجميعية والتبديلية) على الضرب، ويبين الجدول الآتي i = i . 2(12) + التعليم Ministry of Education 2024-1446 بعض قوى الوحدة التخيلية : i2 = -1 13 = i20 i = i 16 = (12)3 = -1 i7 = (12)3. i = -i i4 = (i2)2 = 1 i8 = (2)4 = 1 pure imaginary number العدد المركب complex number المركبان المترافقان complex conjugates الفصل 3 كثيرات الحدود ودوالها 108

i31 (2C مثال 2 أوجد ناتج كلّ مما يأتي : ضرب الأعداد التخيلية البحتة اضرب 2 = -1 −5i • 3i = −15i² -5 . 3i a =-15(-1) بسط = 15 √-6.√-15 (b i=V-1 V-6. V-15 = iV6. i15 اضرب بسط = 12V90 = −1.√√9.√√10 اضرب = -3√√10 √-20.√-12 (2B تحقق من فهمك 3i - 4i (2 يمكنك حل بعض المعادلات التربيعية باستعمال خصائص الجذر التربيعي . مثال 3 معادلة حلولها أعداد تخيلية بحتة حل المعادلة : 0 = 256 + 4x2. 4x²+2560 = 4x²=-256 المعادلة الأصلية اطرح 256 من كلا الطرفين اقسم كلا الطرفين على 4 خاصية الجذر التربيعي x2 = -64 x = +V-64 √-64 = √√√64 • √√−1 = 8i x = ±8i x2 + 4 = 0 (3B تحقق من فهمك 4x2 + 100 = 0 (3A العمليات على الأعداد المركبة تتكون العبارة 23 من حدين غير متشابهين ولا يمكن جمعهما، وهما العدد الحقيقي 2 والعدد التخيلي 3 ويسمى هذا النوع من العبارات العدد المركب. مفهوم أساسي الأعداد المركبة (C) أضف إلي مطويتك التعبير اللفظي: العدد المركب هو أي عدد يمكن كتابته على الصورة ؛ حيث bga عددان حقيقيان، و الوحدة التخيلية، ويسمى d الجزء الحقيقي، وط الجزء التخيلي. 1 – 3i = 1 + (3) وزارة التعليم Ministry of Education الدرس 3-1- الأعداد المركبة 2109140 5+2i مثالان إرشادات للدراسة خصائص الجذر التربيعي راجع خصائص الجذر التربيعي التي درستها في الصف الثالث المتوسط.

إرشادات للدراسة المعاوقة : يوضّح شكل فن المجاور مجموع رعة الأعداد المركبة . . • • إذا كانت 0 = b فإن العدد المركب يكون عددًا حقيقيًّا. إذا كانت 0 b فإن العدد المركب يكون عددًا تخيليا. إذا كانت 0 0 = a فإن العدد المركب يكون عددًا تخيليًا بحتًا. الأعداد المركبة ( a + bi) الأعداد الحقيقية الأعداد التخيلية b = 0 يتساوى عددان مركبان إذا وفقط إذا تساوى الجزأين الحقيقيين، والجزأين التخيليين؛ أي أن: a + bi = c + di إذا وفقط إذا كان a = c, b = d. b0 الأعداد التخيلية البحتة a = 0 مثال 4 تساوي الأعداد المركبة - أوجد قيمتي x y الحقيقيتين اللتين تجعلان المعادلة – y) + 5 - 3 صحيحة. ساو الجزأين الحقيقيين أحدهما بالآخر، وكذلك الجزآن التخيليان. 3x = 12 x = 4 7 = 5 - 3x الجزآن الحقيقيان اجمع 5 لكلا الطرفين اقسم كلا الطرفين على 3 تحقق من فهمك y = 9 6 = 3 - الجزآن التخيليان اجمع 3 لكلا الطرفين. (4) أوجد قيمتي x y الحقيقيتين اللتين تجعلان المعادلة : 6 - 5x +1+3 + 2 = 2 - 2 y صحيحة. جمع ويمكنك استعمال كل من الخاصية التبديلية والخاصية التجميعية وخاصية التوزيع عند الأعداد المركبة وضربها، ولكي تجمع أو تطرح أعدادًا مركبة جمّع الأجزاء المتشابهة؛ أي جمع الأجزاء الحقيقية معا وجمع الأجزاء التخيلية معا. مثال 5 جمع الأعداد المركبة وطرحها أوجد ناتج كل مما يأتي : (57i)+(2+4i) (a (57i) + (2 + 4i) = (5 + 2) + (−7+ 4)i = 7 - 3i (4 - 8i) - (3 - 6i (b - (481) (3 6i) = (4 − 3) + [−8 − (−6)]i = 1 - 2i تحقق من فهمك (−2+5i) + (1 – 7i) (5A خواص التبديل والتجميع والتوزيع بسط خواص التبديل والتجميع والتوزيع بسط (4 + 6i) − (−1 +2i) (5B في الأعداد المركبة تستعمل الأعداد المركبة في مسائل الكهرباء، ففي الدوائر الكهربائية ذات التيار المتناوب يمكنك تمثيل فرق تستعمل كلمة المعاوقة الجهد، وشدة التيار، والمعاوقة بأعداد مركبة، ولضرب هذه الأعداد تستعمل طريقة التوزيع بالترتيب. بدلا من المقاومة وزارة التعليم 110 الفصل 3 كثيرات الحدود ودوالها Ministry of Education 2024-1446

الربط مع الحياة مصابيح الزينة من الأمثلة على الدوائر الكهربائية الموصولة على التوالي، ويؤثر عدد المصابيح فيها في شدة التيار، فينعكس هذا على شدة الإضاءة. إرشادات للدراسة قراءة الرياضيات يمكنك حل الفرع b من المثال 7 بضرب كل من البسط والمقام في العدد 5i- ، ولكن للاختصار تم الضرب في العدد i فقط. مثال 6 من واقع الحياة ضرب الأعداد المركبة كهرباء: يرتبط فرق الجهد V، وشدة التيار C، والمعاوقة I في الدوائر الكهربائية ذات التيار المتناوب بالصيغة V=CI. أوجد فرق الجهد في دائرة كهربائية ذات تيار متردد إذا كانت شدة تيارها 4 + 2 أمبير، ومعاوقتها 3 – 9 أوم . V = C.I الصيغة الرياضية C = 2 + 4i, I = 9 - 3i باستخدام طريقة التوزيع بالترتيب اضرب =(2+41) (9 - 3i) = 2(9) + 2(−3i) + 4i(9) + 4i(-3i) 18 6i36i - 12i² = – = 18+ 30i - 12(−1) = 30 + 30i i2 = -1 اجمع وعليه فإن فرق الجهد هو 30i + 30 فولت. تحقق من فهمك (6) كهرباء أوجد فرق الجهد لتيار متناوب شدته 4i - 2 أمبير، ومعاوقته 2i - - 3 أوم. يسمى a - و العددان المركبان a + bi bi مركبين مترافقين، وناتج ضربهما هو عدد حقيقي دائمًا على الصورة 2 + 2. ويمكنك استعمال هذه الحقيقة لإيجاد ناتج قسمة عددين مركبين. مثال 7 قسمة الأعداد المركبة أوجد ناتج كل مما يأتي: (a (b 2i 3 + 6i 5i +5 4 + i 2i 2i 3- 6i = • 3+6i 36i 3- 6i 6 - 63 + 3 مترافقان مركبان 6i - 12i² اضرب = 9-3612 6i-12(-1) i2 = -1 = 9-36(-1) تحقق من فهمك -2i 3+5i (7 6i + 12 45 = 1 + 4 2 i 15 15 4 + i 4 + i i = • 5i 5i 4i + i2 i بسط اكتب الناتج على الصورة a + bi اضرب في i _ i اضرب 5i2 i2 = -1 4i - 1 = -5 = اكتب الناتج على الصورة a + bi 2+i 1 (78) وزارة التعليم Ministry of Education الدرس 1-3 الأعداد المركبة 211114

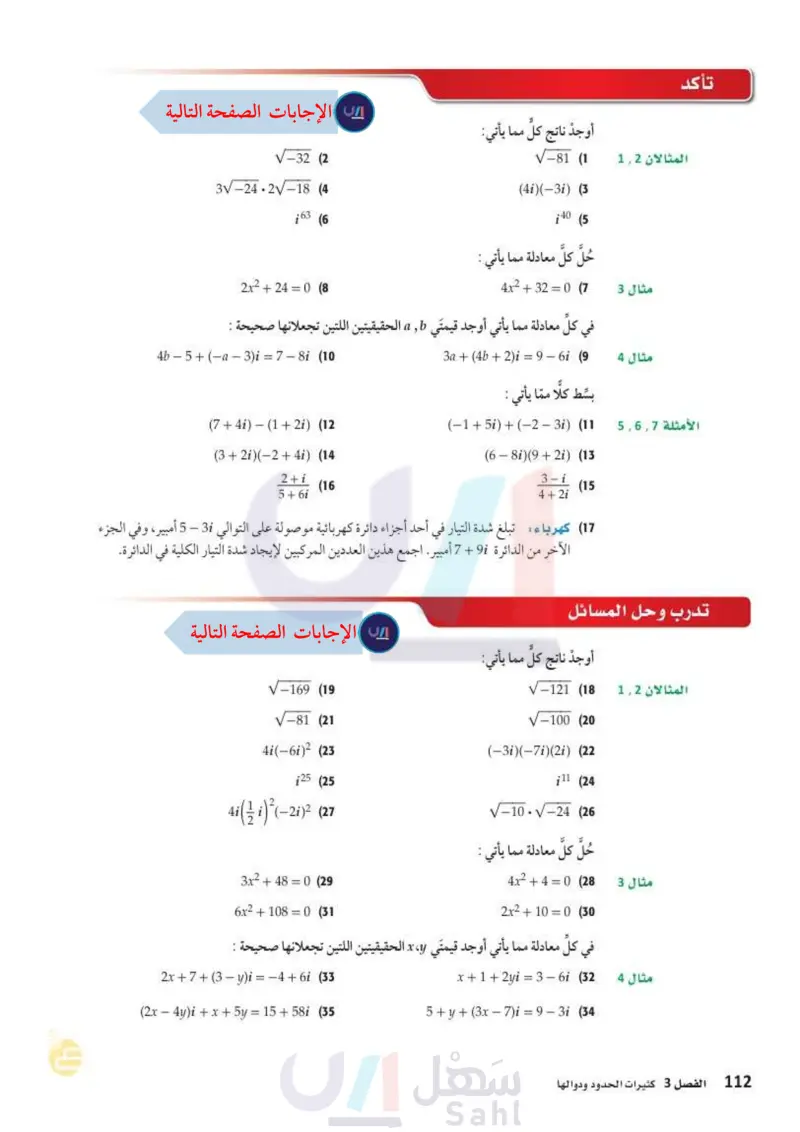
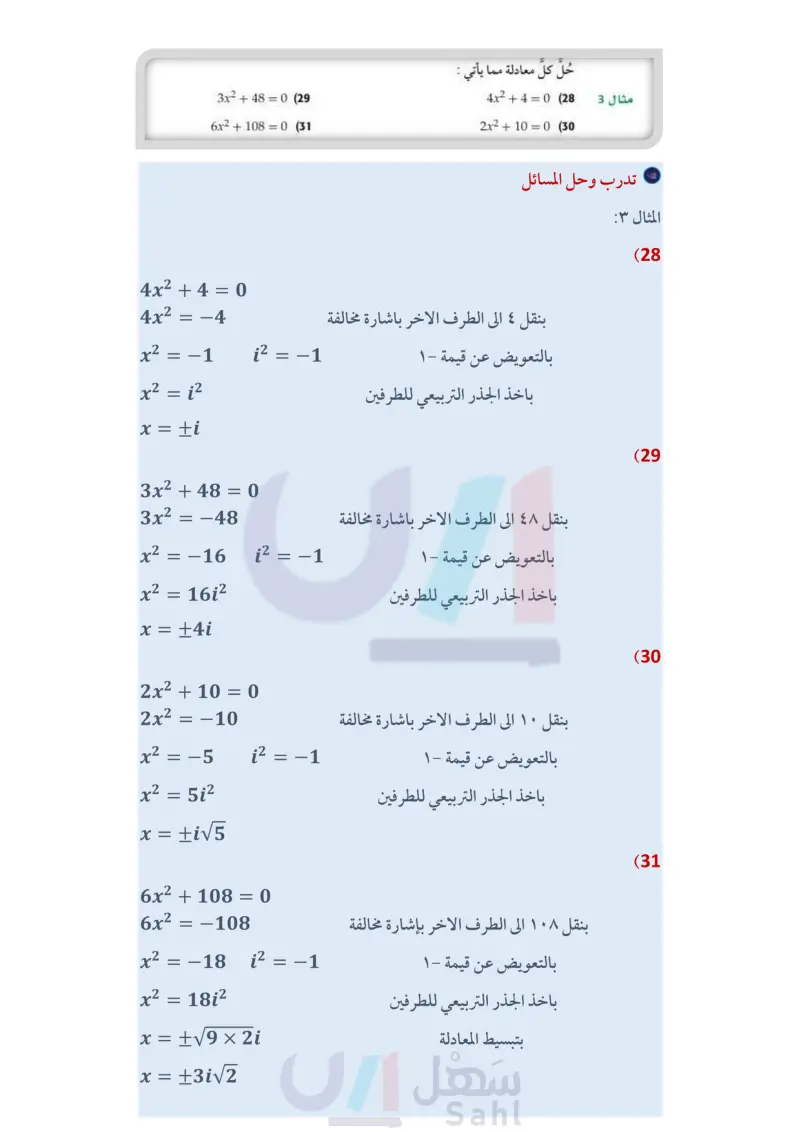
112 تأكد المثالان 12 أوجد ناتج كل مما يأتي: V-81 (1 (41)(-3i) (3 40 (5 حل كل معادلة مما يأتي : -32 (2 3√-24.2√-18 (4 163 (6 مثال 3 4x2 + 32 = 0 (7) 2x2 + 24 = 0 (8 b , في كل معادلة مما يأتي أوجد قيمتي الحقيقيتين اللتين تجعلانها صحيحة : مثال 4 3a + (4b+2)i = 9—6i (9 - 4b 5+(-a-3)i = 7-8i (10 الأمثلة 5,6,7 بسط كلا مما يأتي : (-1+5i)+(-2-3i) (11 (6-8i)(9+2i) (13 3-i (15 4 + 2i (741) (1+2i) (12 - (3+2i)(-2+4i) (14 2+i (16 5+6i : (17) كهرباء تبلغ شدة التيار في أحد أجزاء دائرة كهربائية موصولة على التوالي 3i – 5 أمبير، وفي الجزء الآخر من الدائرة 9 + 7 أمبير. اجمع هذين العددين المركبين لإيجاد شدة التيار الكلية في الدائرة. تدرب وحل المسائل المثالان 2 1 ' مثال 3 مثال 4 أوجد ناتج كل مما يأتي: -121 (18 √-169 (19 -100 (20 √-75 (21 4i(-6i)² (23 (-3i)(-7i)(2i) (22 11 (24 25 (25 4i (i)² (-2)² (27 V-100-24 (26) حُلَّ كل معادلة مما يأتي : 4x2 + 4 = 0 28 2x2100 (30 3x²+480 (29 = 6x2+1080 (31 كل معادلة مما يأتي أوجد قيمتي x y الحقيقيتين اللتين تجعلانها صحيحة : x+1+2yi = 3-6i (32 5+y+(3x-7)i=9-3i (34 الفصل 3 كثيرات الحدود ودوالها 2x+7+(3-y)i = -4+6i (33 (2x-4y)i+x+5y = 15+58i (35 وزارة التعليم Ministry of Education 2024-1446

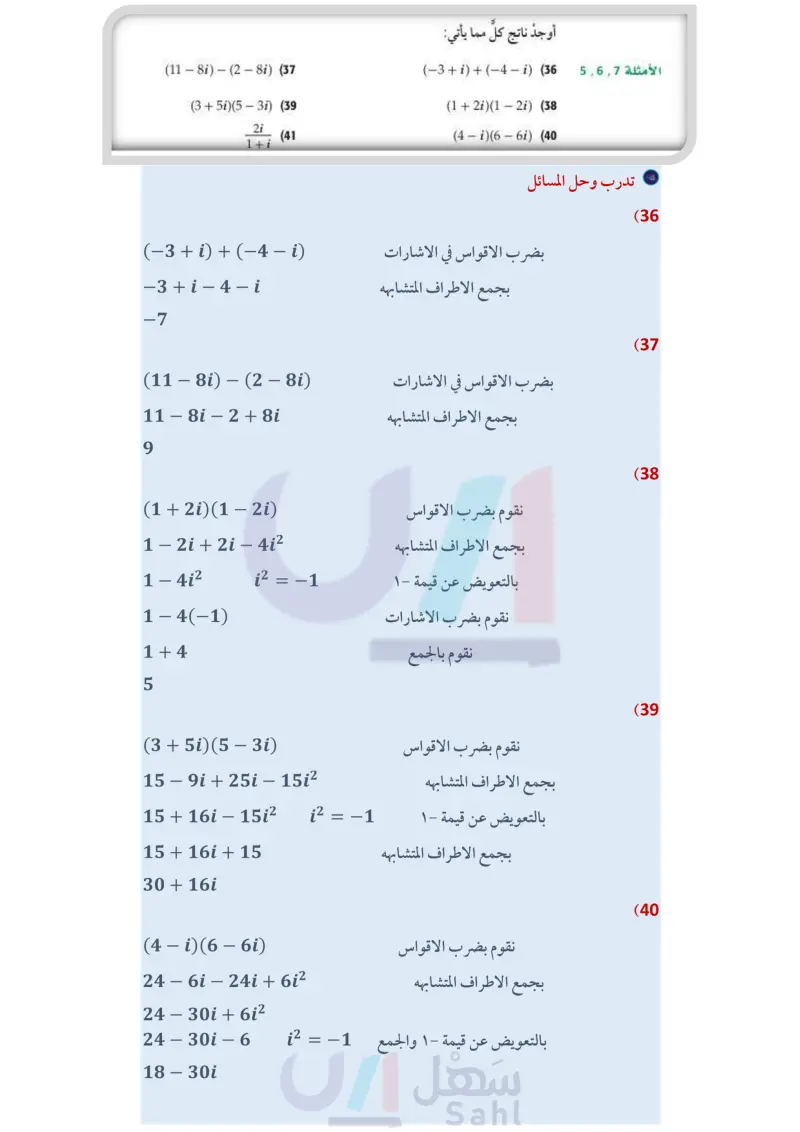
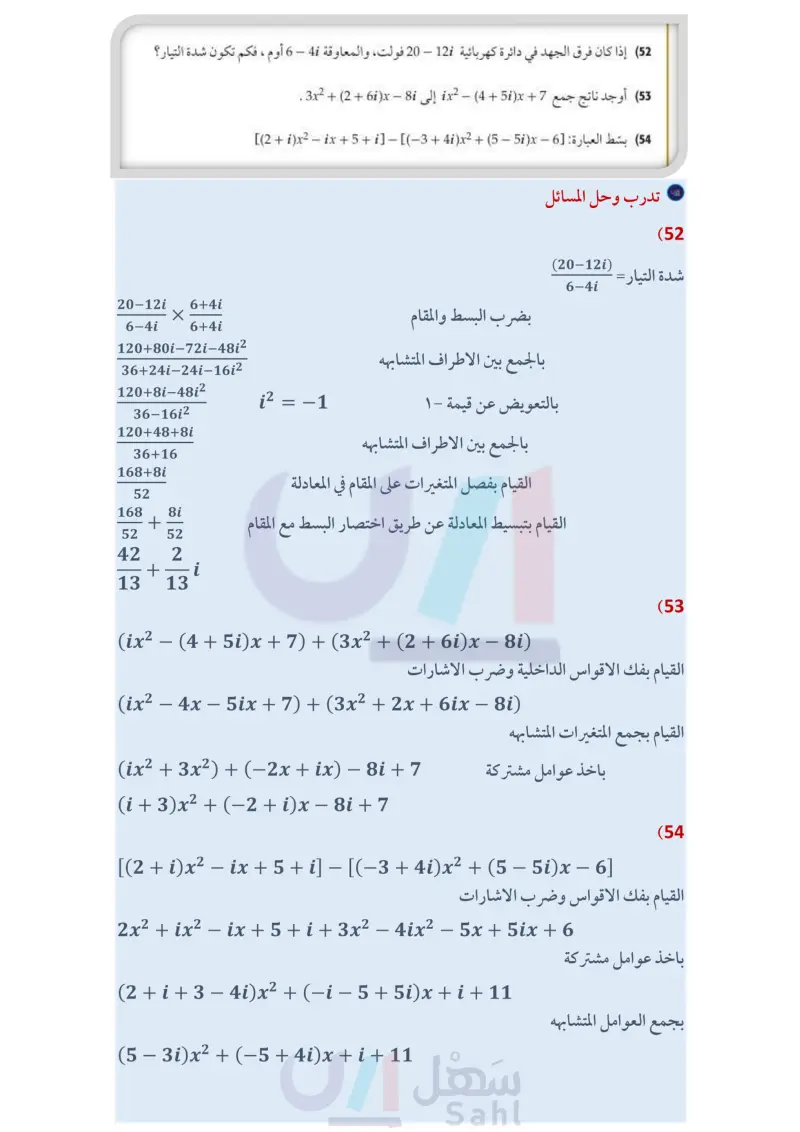
أوجد ناتج كل مما يأتي: - (11 - 8i) (28i) (37 (35i)(53i) (39 2i (−3 + i) + (-14 - (i) (36 (1+2i)(12i) (38 (4-i)(66i) (40 (41 1 + i 5+i 3i (43 ― (85i) (7+i) (45 (1 + i)(2+3i)(4 - 3i) (47 2-i√√3 (49 2+i√3 5 (42 2 + 4i (4 - 6i) + (4 + 6i) (44 (−6 – i)(3 – 3i) (46 4 - i2 (48 4 + i2 : 7+ (50 كهرباء تبلغ المعاوقة في أحد أجزاء دائرة كهربائية ++ أوم، وفي الجزء الآخر منها 4i – 13 أوم. اجمع هذين العددين المركبين لإيجاد المعاوقة الكلية في الدائرة الكهربائية. كهرباء استعمل الصيغة V = CI، حيث V فرق الجهد، وC شدة التيار، و I المعاوقة في حل السؤالين 52 51 : (51) إذا كانت شدة التيار في دائرة كهربائية 6 + 3 أمبير، والمعاوقة 1 - 5 أوم ، فكم يكون فرق الجهد ؟ (52) إذا كان فرق الجهد في دائرة كهربائية 12 - 20 فولت، والمعاوقة 4 - 6 أوم ، فكم تكون شدة التيار؟ . 3x² + (2 + 6i)x−8i Jix² - (4+5i)x+7(53 أوجد ناتج جمع (54) بسط العبارة: 61 - ix2 - ix + 5 + i] - [(-3 + 4ix2 + (5) - 5ix + 2)] (55) تمثيلات متعددة: ستكتشف في هذه المسألة جمع الأعداد المركبة في المستوى المركب. فالمستوى المركب يشبه إلى حد بعيد المستوى الحقيقي، وفيه تكون الأعداد الحقيقية على المحور الأفقي والأعداد التخيلية البحتة على المحور الرأسي. الأمثلة 567 الربط مع الحياة الكهرباء هي عدد من التأثيرات الفيزيائية تشمل مجموعة متنوعة من الظواهر الناتجة عن وجود شحنة كهربائية وتدفقها. وتضم هذه الظواهر البرق، والكهرباء الساكنة والمجال والحث الكهرومغناطيسيين. (a بيانيا : مثل العدد 4 + 3 بيانيًا في المستوى المركب، وذلك بر قطعة مستقيمة من نقطة الأصل إلى النقطة (3)، وسمّ تلك النقطة A. برسم ( بيانيا : مثل العدد 5 - 2 بيانيًّا في المستوى المركب وذلك قطعة مستقيمة من نقطة الأصل إلى النقطة (25)، وسمها . برسم بيانيًّا : إذا كانت النقطتان .A.B ونقطة الأصل ثلاثة رؤوس لمتوازي أضلاع فأكمل و النقطة الرابعة C d) تحليليا : ما العدد المركب الذي تمثله النقطة C ؟ وما العلاقة بين النقاط A,B,C رسمه بإضافة وزارة التعليم Ministry of Education الدرس 1-3 الأعداد المركبة 211314

مسائل مهارات التفكير العليا 56) اكتشف الخطأ : قامت كلٌّ من صفاء ومنال بتبسيط (4)(3)(2)، فأي منهما على صواب؟ وضّح إجابتك. صفاء 24i3 =-24i منال 24i3=-24 (57) تحد: بسط العدد المركب (12). 58) تبرير: حدد إذا كانت الجملة الآتية صحيحة دائمًا، أو صحيحة أحيانًا، أو غير صحيحة أبدًا. وضّح إجابتك: " يتكون كل عدد مركب من جزء حقيقي وجزء تخيلي' "" تدريب على اختبار (59) مسألة مفتوحة اكتب عددين مركبين يكون ناتج ضربهما يساوي 20. 60 اكتب وضّح كيف ترتبط الأعداد المركبة بالمعادلات التربيعية، وكيف تحدد إذا كان للمعادلة التربيعية حلول مركبة فقط أم لا ؟ (61) ما قيمتا x y الحقيقيتان اللتان تجعلان (1-3-) = (xyi) - (4 + 5) صحيحة ؟ (62) قيمة ( 36 ) تساوي: x = 6, y = 7 (A x = 4,y = i (B x = 4,y = i (C x = 4,y=7(D مراجعة تراكمية 36-27i (A 9 +36 (B 9-36 (C -27 +36i (D حُلَّ كلّ معادلة مما يأتي مستعملا التحليل إلى العوامل (مهارة سابقة) 2x2 + 7x = 15 (63 4x2 - 12 = 22x (64) 6x2 = 5x + 4 (65) نظرية الأعداد : استعمل معادلة تربيعية لإيجاد عددين حقيقيين يحققان كلًا مما يأتي، (إذا كان ذلك ممكنا ) (مهارة سابقة) (66) مجموعهما 3، وناتج ضربهما 40 - น هل تمثل كل من ثلاثيات الحدود الآتية مربعا كاملًا أم لا؟ (مهارة سابقة) 67) مجموعهما 21-، وناتج ضربهما 108 x2 + 16x + 64 (68) x2 + 8x - 16 (70 114 الفصل 3 كثيرات الحدود ودوالها x2 - 12x + 36 (69) x2 + 5x + 6.25 (71 وزارة التعليم Ministry of Education 2024-1446