توسع المصفوفات الموسعة - رياضيات2-1 - ثاني ثانوي
الفصل الأول: الدوال والمتباينات
الفصل الثاني: المصفوفات
الفصل الثالث: كثيرات الحدود ودوالها
نشاط الفصل الأول: الدوال والمتباينات
نشاط الفصل الثاني: المصفوفات
نشاط الفصل الثالث: كثيرات الحدود ودوالها
V رابط الدرس الرقمي www.ien.edu.sa معمل الحاسبة البيانية المصفوفات الموسعة توسع 2-5 الهدف أستعمل الحاسبة البيانية TI-nspire والمصفوفة الموسعة لحل نظام معادلات خطية. يُمكنك حَلّ نظام معادلات خطية باستعمال الحاسبة البيانية TI - nspire، إذ تحتوي المصفوفة الموسعة على مصفوفة المعاملات مع عمود إضافي إلى اليمين يحوي الثوابت وباختزال المصفوفة الموسعة يصبح من السهل تحديد حل نظام من المعادلات. مثال اكتب مصفوفةً موسعةً لنظام المعادلات الآتي، ثم حُلَّ هذا النظام باستعمال الحاسبة البيانية: B المستندات المسودة العمليات الحسابية 2 مستنداتی B الرسم البياني 1 مستند جدید 3 الأخيره 4 الحالي 5 الإعدادات لم يتم الحفظ إنشاء مصفوفة المصفوفة عدد الصفوف | 3 عدد الأعمدة موافق الغاء 1.1 2x + y + z = 1 3x + 2y + 3z = 12 4x + y + 2z = -1 الخطوات: • • افتح الآلة الحاسبة بالضغط على Mon من الشاشة الظاهرة اختر A العمليات الحسابية ومنها اختر 1 مستند جدید اختر 1 إضافة تطبيق الحاسبة ثم اختر [7: المصفوفات و المتجهات ومنها اختر menu اضغط على مفتاح . • • • 1: إنشاء ومنها 1: المصفوفة فتظهر شاشة نحدد من خلالها عدد الصفوف وعدد الأعمدة. أدخل عدد الصفوف ثم اضغط ) اضغط enter 0/99 18x: الإجراءات 25: العد1: إنشاء 3x العم 2 تبديل الصف بالعمود وأدخل عدد الأعمدة ثم 4f: التفا3 محدد المصفوفة tab أدخل معاملات المتغيرات والثوابت مستعملا للتنقل، ثم اضغط enter اضغط doc واختر منها 1 ملف الملف واضغط حفظ اضغط (menu) 5: حفظ باسم ... ثم سم اختر [7: المصفوفات و المتجهات ومنها اختر Reduced Row-Echelon Form :5 استعمل السهم لأعلى لتظلل المصفوفة الموسعة التي كتبتها ثم اضغط enter enter مرة أخرى فيظهر الحل. الإ4 Row-Echelon Form Reduced Row-Echelon Form :5 y1:6 X [0]7 الم 6 حل نظام المعادلات باستخدام المصفوفات :8 :الما 7: مقياس المصفوفة 9 الدو8: أبعاد المصفوفة 0/99 :9 العمليات على الصفوف A العمليات على العناصر matricies 1.1 2 1 1 1 2 1 1 1 3 23 12 4 12 1 rref 2 1 3 2 3 12 3 23 12 4 1 2 -1 100-4 0 1 0 3 6 2/99 12 13 4 1 2 1 0 0 1 ادرس الشكل المختزل للمصفوفة، ولاحظ أن الأعمدة الثلاثة الأولى تشكّل مصفوفة محايدة من الرتبة 3 × 3 ، وتستنتج من الصف الأول أن 4 = x، ومن الصف الثاني أن 3 = y، و من الصف الثالث أن 6 = 2 ، وعليه يكون الحل . ' تمارين : اكتب مصفوفةً موسعةً لكل نظام معادلات فيما يأتي، ثم حُلَّه باستعمال الحاسبة البيانية: 6x+4y+2z = -4 (3 . 2x-2y+6z= 10 ورة التعليم 2x + 2y + 2z Ministry of Education = −2 4x + 6y = 0 (2) 8x - 2y = 7 توسع - معمل الحاسبة البيانية: المصفوفات الموسعة 1 - 297 3x + 2y = -4 (1) 4x + 7y = 13

الفصل 2 دليل الدراسة والمراجعة ملخص الفصل المفاهيم الأساسية المصفوفات (الدرس 1-2) المفردات المصفوفة (62) العنصر (62) الرتبة (62) • المصفوفة : هي ترتيب على هيئة مستطيل لمتغيرات أو مصفوفة الصف (63) أعداد في صفوف أفقية وأعمدة رأسية بين قوسين. المصفوفات المتساوية لها الرتبة نفسها، وعناصرها المتناظرة متساوية. العمليات على المصفوفات (الدرسان 2-2 و 3-2) . يمكن جمع المصفوفات أو طرحها إذا كان لهما الرتبة نفسها. وذلك العناصر المتناظرة أو طرحها. بجمع لضرب مصفوفة في عدد ثابت ، اضرب كل عنصر من عناصر المصفوفة في هذا العدد. k مصفوفة العمود (63) المصفوفة المربعة (63) المصفوفة الصفرية (63) المصفوفات المتساوية (63) جمع مصفوفتين (69) طرح مصفوفتين (69) ضرب المصفوفة في عدد ثابت (70) . يمكن ضرب مصفوفتين إذا كان عدد أعمدة الأولى يساوي المحددة (83) عدد صفوف الثانية. المحددات وقاعدة كرامر (الدرس 4-2) و اختبر مفرداتك محددة الدرجة الثانية (83) محددة الدرجة الثالثة (84) قاعدة الأقطار (84) مصفوفة المعاملات (86) قاعدة كرامر (86) مصفوفة الوحدة (91) النظير الضربي للمصفوفة (91) المعادلة المصفوفية (93) مصفوفة الثوابت (93) مصفوفة المتغيرات (93) اختر الكلمة المناسبة من المفردات أعلاه لتكمل كل جملة فيما يأتي: . قيمة محددة المصفوفة المربعة من الرتبة 2 × 2 تساوي حاصل ضرب عنصري القُطر الرئيس مطروحًا منه حاصل 1) الترتيب على هيئة مستطيل لمتغيرات أو أعداد في صفوف أفقية وأعمدة ضرب عنصري القطر الآخر. . تستعمل المحددات في حل أنظمة المعادلات الخطية، وفي إيجاد مساحة مثلث علمت إحداثيات رؤوسه. النظير الضربي للمصفوفة وأنظمة المعادلات الخطية (الدرس 5-2 مصفوفة الوحدة هي مصفوفة مربعة عناصر القطر الرئيس فيها العدد 1 وباقي العناصر أصفار. رأسية تكتب بين قوسين يسمى. (2) عملية ضرب جميع عناصر المصفوفة في عدد تسمى (3) تُسمى المصفوفة التي تحوي الثوابت في نظام المعادلات (4) كل قيمة في المصفوفة تُسمى . تكون كل من المصفوفتين نظيرًا ضربيًّا للأخرى إذا كان (5) يُسمى عدد الصفوف × عدد الأعمدة في المصفوفة . حاصل ضربهما يعطي مصفوفة الوحدة. . لحل معادلة مصفوفية من الشكل AX = B، أوجد النظير الضربي لمصفوفة المعاملات، ثم اضرب طرفي المعادلة فيه. المطويات منظم أفكار تأكد من أن المفاهيم الأساسية مدونة في مطويتك. المصفوفة. (6) المصفوفة المربعة التي عناصر القطر الرئيس فيها العدد 1 وباقي العناصر أصفار هي (7) المصفوفة التي جميع عناصرها أصفار هي 2 -1 2 - المصفوفات | (8) قيمة . المصفوفة [3- 3 | تساوي 1-. 98 الفصل 2 المصفوفات (9) إذا كان حاصل ضرب مصفوفتين هو مصفوفة الوحدة، فإن كلتا المصفوفتين تكون للأخرى. وزارة التعليم Ministry of Education 2024-1446

مراجعة الدروس 2-1 مقدمة في المصفوفات الصفحات: 67-62) 10) ناد رياضي : يبين الجدول الآتي عدد المشتركين شهريا وسنويًا في نادٍ رياضي في 3 رياضات مختلفة: مثال 1 متحف يبين الجدول الآتي عدد زوار متحف في الفترة الصباحية والفترة المسائية خلال 3 أيام 2-2 اللياقة البدنية السباحة تخفيض الوزن 64 108 31 42 9 68 اشتراك شهري اشتراك سنوي نظم بيانات الجدول في المصفوفة 4 . ما رتبة المصفوفة A؟ ما قيمة العنصر a23؟ d) ما قيمة العنصر a11؟ اجمع عناصر كل من الصفين الأول والثاني، وفسر النتائج. العمليات على المصفوفات الصفحات: 76-71) أوجد الناتج في كل مما يأتي، إذا كان ذلك ممكنا: -6 37 69 اليوم الثالث اليوم الأول اليوم الثاني 26 75 الفترة الصباحية الفترة المسائية 19 58 [ 37 19 26 69 58 75 a اكتب مصفوفة تمثل عدد الزوار ما رتبة المصفوفة؟ 3 × 2 اجمع عناصر كل من الصفين 1 و 2، وفسّر النتائج. مجموع عناصر الصف 1 هو ،82، ويمثل عدد الزوار في الفترة الصباحية للأيام الثلاثة ومجموع عناصر الصف 2 هو 202، ويمثل عدد الزوار في الفترة المسائية للأيام الثلاثة. مثال 2 أوجد ناتج 3 + 2 إذا كانت 2 -3 + 2 [6] (11 [ 2 8 6 14 4 ] -2 0 3 6 8 29 11 9 20 2] [ - [3 : + (12 1 4 3 7 = 9 .B 1 2 9 3A = = 2 27 4 1 34-3 [11] - [33] 28-23 1 ] - 6 , 2B = 8 2 27 7 = 28 + 34 - [313] + [33] - [23 = 2B 3A 6 14 = 6 2-3 ضرب المصفوفات الصفحات: 83-77) أوجد الناتج في كل مما يأتي، إذا كان ذلك ممكنا: مثال 3 9 -71. [31] [3 -7] [211]. [08-5] (13 -5 (14 (15) مشتريات اشتری راشد 4 علب حليب ، و 2kg تفاحًا، و 3kg بطاطس، وكيسًا واحدًا من الأرز، وتبين المصفوفة أدناه سعر علبة الحليب، والكيلوجرام الواحد من التفاح والكيلوجرام الواحد من البطاطس، وكذلك سعر كيس الأرز. أرز بطاطس تفاح حليب 10 [15 25] 3 استعمل ضرب المصفوفات لإيجاد إجمالي المبلغ الذي دفعه راشد. -6 0 5 x= [33] x- [1] 8 Y: xx = [ 3 ] XY = أوجد XY إذا كانت -6 5 [-] 8 0(8)+(-6)(-1) 3(8) +5(-1) = - [ 19 ] 6 اضرب الصفوف في الأعمدة بسط وزارة التعليم Ministry of Education. الفصل 2 دليل الدراسة والمراجعة 1 - 299
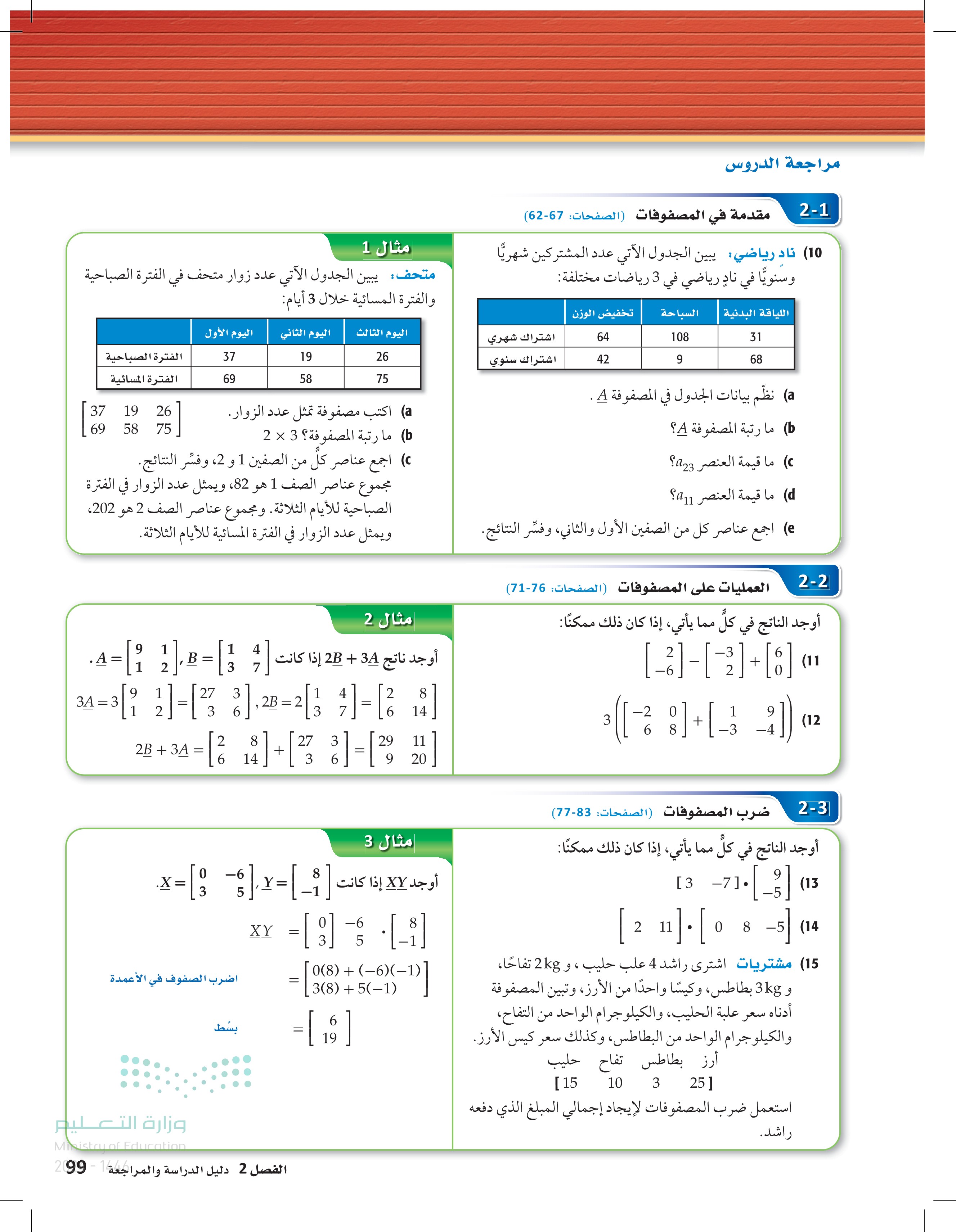
اكتب مصفوفة تمثل عدد الزوار.
أوجد ناتج 2B+3A
أوجد XY
تعريف محددة الدرجة الثانية بسط 21 −1 2 b = 2 6 89 21 = 4+1 16 == 6 5 10 12 4 +2 مثال 4 الفصل 2 دليل الدراسة والمراجعة 2-4 المحددات وقاعدة كرامر (الصفحات: 92-85) أوجد قيمة كل محددة فيما يأتي: 2 4 -6 2 5 أوجد قيمة: | 0 2 32 1 4 (17 2 4 7 -3 | (16 -2 5 6 -6 5 =4(5) - 2(-6) استعمل قاعدة كرامر لحل كل نظام معادلات فيما يأتي: = 20 +12=32 مثال 5 استعمل قاعدة كرامر لحل النظام: 2a + 6b = -1 a + 8b = 2 ' قاعدة كرامر احسب المحددات بسط || = 2 -1 6 2 8 6 1 8 -8 - 12 16-6 -20 = -2 10 (-2, 1/1) الحل هو 3x - y = 0 (18 5x + 2y = 22 5x+2y=4 (19 3x + 4y + 2z = 6 7x + 3y + 42 = 29 4z (20) حرف يدوية : صنعت شيماء 3 أساور، وعقدين بتكلفة مقدارها 85 ريالا، وصنعت ليلى سوارين و 4 عقود بتكلفة مقدارها 110 ريالات . فإذا كان للعقود التي صنعتها كل منهما العقد، التكلفة نفسها، وكذلك الأساور. فجد تكلفة كل من والسوار. 2-5 النظير الضربي للمصفوفة وأنظمة المعادلات الخطية الصفحات: 98-93) أوجد النظير الضربي لكل مصفوفة فيما يأتي، إن وجد: مثال 6 15 36 2 حل المعادلة المصفوفية: [35] - [4] [35] −5 -6 x y = جد النظير الضربي لمصفوفة المعاملات. الخطوة 1: -6 5 A-1=-12-(-15) [ ] = [1] Α -6 5 -3 2 3-3 2 الخطوة 2 حل المعادلة المصفوفية باستعمال X = A-1 B : وزارة التعليم Ministry of Education 2024-1446 x 6 5 [{} ] } [1] • [156] y = 3 1 -3 [i] - [2] x = 3 30 = [✓] - [39] 2].[3] 36 2 5 (22 -5 -13 7 [3] 4 (21 2 6 -3 (23 -8 + حل المعادلة المصفوفية فيما يأتي: 5 3 3 2 -1 4 {] • [x] = [8] a 5 [32][0] - [4] = (24 (25 26 مشتريات اشتری سعود 2kg مكسرات و 2kg قهوة بمبلغ 140 ريالًا. واشترى ناصر 3kg مكسرات وكيلوجرامًا إذن الحل هو (309) قهوة بمبلغ 170 ريالًا . فما سعر الكيلوجرام الواحد من كلا النوعين؟ الفصل 2 المصفوفات 100

مثال 4 أوجد قيمة
مثال 5 استعمل قاعدة كرامر لحل النظام
مثال 6 حل المعادلة المصفوفية
8) -4 7 2 0 5 5 إذا كان [ 3 - 3 - 3 -4 8 ,B -4 A- [ فأوجد ناتج AB - AC الفصل 2 اختبار الفصل = A ، فحدد قيمة كل عنصر مما يأتي: فحدد قيمة كـ 931 (2) 2 2 7 298 9 1 8 0 8 إذا كانت 1 922 (1 أوجد الناتج في كلُّ مما يأتي، إذا كان ذلك ممكنا: - -2 3 (3 −1 4a -3 +4 -3 (9) استعمل المحددات لإيجاد مساحة Axyz الذي رؤوسه . x(1, 2), y(3, 6), z(−1, 4) (10) اختيار من متعدد أوجد قيمة محددة المصفوفة: 2 0 2 -2 325 1 4 5 6 C 44 D 44 - 44 A 44 B -3 0 [ ¯ {} } ] · [ 1 ] 44 1 5 2 4 -6 0 (4 أوجد النظير الضربي لكل مصفوفة فيما يأتي، إن وجد: 1 2 [2 1] ] (12 [33] « (14 0 [59] 0 (11 6 3 8 4 (13 2 0 -3 5 1 4 • 7 - و] - [38] -5 6 3 -2 (5 4 0 (6 9 0 1 (7) مبيعات تبيع مكتبة 3 مجموعات من كتب الأطفال. ويبين الجدول الآتي تكلفة كل مجموعة وسعر بيعها. فإذا باعت المكتبة الكتب 20 مجموعة من الكتب التربوية و 32 مجموعة من الكتـ العلمية، و 14 مجموعة من القصص. استعمل معادلة مصفوفية لحل نظام المعادلتين الآتي: 2x - y = −9 (15 x + 2y = 8 استعمل قاعدة كرامر لحل كل نظام معادلات فيما يأتي: وزارة التعليم Ministry of Education الفصل 2 اختبار الفصل 2101144 x - y + 22 = 0 (16 3x + z = 11 - x + 2y = 0 6x + 2y + 42 = 2 (17 3x + 4y - 8z = -3 -3x-6y+ 12z = 5 سعر البيع (ريال) المجموعة التكلفة 100 120 90 110 130 150 تربوية علمية قصص (a نظم البيانات في مصفوفات، ثم استعمل ضرب المصفوفات لإيجاد تكلفة الكتب الكلية. استعمل ضرب المصفوفات لإيجاد المبلغ الكلي الذي تحصلت عليه المكتبة من بيع ذلك العدد من مجموعات الكتب. ( استعمل العمليات على المصفوفات لمعرفة ربح المكتبة.

عليم 0000000 3 3 3 0000 الإعداد للاختبارات المعيارية الفصل 2 أسئلة الإجابات الشبكية من المحتمل أن تواجه في الاختبارات المعيارية بالإضافة إلى أسئلة الاختيار من متعدد، وأسئلة الإجابات القصيرة، وأسئلة الإجابات المطولة، أسئلة الإجابات الشبكية. ويتطلب هذا النوع من الأسئلة كتابة الإجابة في نموذج خاص، وذلك بتظليل الدوائر التي تمثل الإجابات الصحيحة. استراتيجيات حل أسئلة الإجابات الشبكية الخطوة 1 اقرأ المسألة بإمعان، ثم حلّها. . تأكد من أن إجابتك لها معنى. . إذا كان الوقت كافيًا، فتحقق من إجابتك. 10 3 5 5 5 5 5 5 6 6 6 6 5 6 56 7 8 8 9 9. 8 8 8 9 1 4 3 0000 000000 5000000 3 3 4 5 5 5 6. 6 6 6 6. 6. 6 8 8 8 8 8 8. 8 8. 9 9 9 9 000000000 0000 3 4 4 5 6 6 8 8 8 8 9 9 9 9 Ministry of Education 2024-1446 الخطوة 2 . اكتب إجابتك في مربع الإجابة. اكتب عددًا واحدًا فقط أو رمزًا في كل مربع إجابة على نموذج الإجابة الشبكية. . لا تكتب أي أرقام أو رموز خارج مربعات الإجابة. . يمكن أن تكون إجابات هذه الأسئلة أعدادًا كلية أو كسورًا عشرية، أو كسورًا اعتيادية. الخطوة 3 دوّن الإجابة في نموذج الإجابة الشبكية. . ظلّل دائرة واحدة فقط لكل مربع إجابة، وتأكد من أنك ظللت قيمة مناظرة للتي في المربع. . ظلّل بصورة واضحة وكاملة. مثال اقرأ المسألة الآتية جيدًا، وحدّد ما تحتاج إلى معرفته، ثم استعمل المعطيات لحلها. زوّد محمد سيارته بالوقود مرتين في أثناء سفره إلى الرياض قادمًا من مكة المكرمة. فإذا كان سعر البنزين في المحطة الأولى 1.50 ريال لكل لتر، وفي المحطة الثانية كان السعر 1.45 ريال لكل لتر، وكان مجموع ما زوّد به سيارته من البنزين 100 لتر بسعر إجمالي 147.25 ريالا. فكم لتر بنزین زود به سيارته من كل محطة؟ الفصل 2 المصفوفات 102
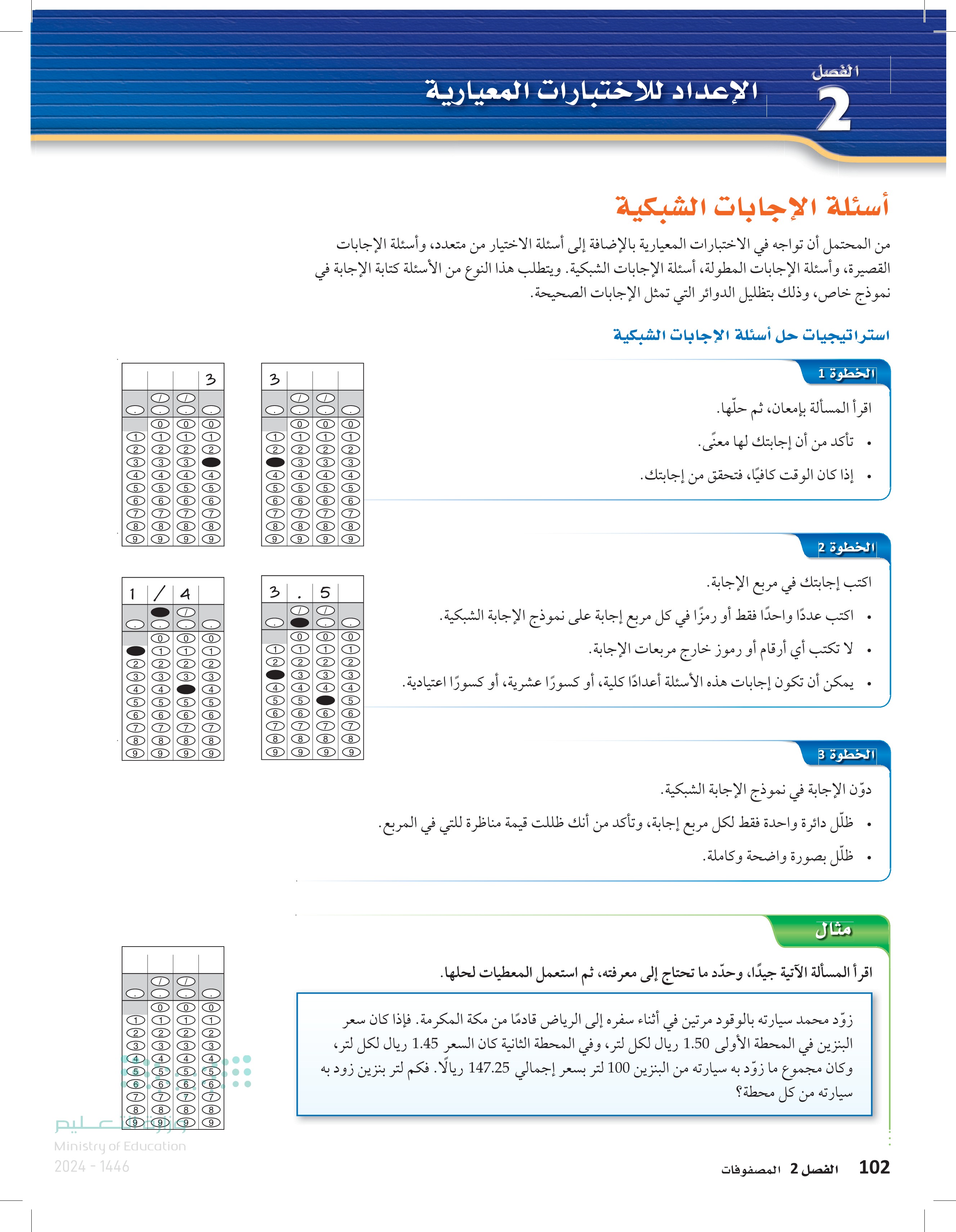
استراتيجيات حل أسئلة الإجابات الشبكية
اقرأ المسألة الآتية جيدا، وحدد ما تحتاج إلى معرفته ، ثم استعمل المعطيات لحلها.
اقرأ المسألة جيدا، إذ يمكن حلها باستعمال نظام من معادلتين. لتكن x تمثل عدد اللترات من المحطة الأولى، و لا تمثل عدد اللترات من المحطة الثانية، لذا يكتب نظام المعادلتين الذي يمثل هذه الحالة على النحو الآتي: x + y = 100 1.50x + 1.45y = 147.25 من الممكن حل هذا النظام جبريًا، ولكن يمكن حله بشكل أسرع وبطريقة أسهل باستعمال المصفوفات والحاسبة البيانية. حل المسألة أدخل كلًا من مصفوفة المعاملات ومصفوفة الثوابت إلى الحاسبة البيانية، ثم أوجد الحل باستعمال النظير الضربي. 45 [1.50 1.45]-[14225] } ] = [ 5 ] y 100 = [ y 55 إذن زوّد محمد سيارته بـ 45 لترًا من المحطة الأولى ، و 55 لترا من المحطة الثانية. تمارين ومسائل 4 45 000000 100 00000000 4 00 8 8 8 9 9 9 9 اقرأ كل مسألة، وحدّد ما تحتاج إلى معرفته، ثم استعمل المعطيات لحلها. انسخ نموذج الإجابة، واستعمله في الإجابة. [ 20 ] 4 -1 -3 (2 أوجد محددة المصفوفة (2 (1) أوجد محددة المصفوفة -2 0 3 H=-5 -7 -1 4-8 1 وزارة التعليم Ministry of Education الفصل 2 الإعداد للاختبارات المعيارية 210314

اختبار تراكمي الفصل 2 أسئلة الاختيار من متعدد اختر الإجابة الصحيحة فيما يأتي: 1) إذا كانت [ -2 1 3 1 03 2 B = 33 32 13 ] فما قيمة 3B + 24 ؟ (5) ما النظام الذي تمثل حله المنطقة المظللة في الشكل أدناه؟ co 6x y 3x + 4y = 12 4x + 2y = 8 321 -1 -5-4-3-2-10 1 2x - 6y = 12. 1234 -4 - 4x + 2y ≥ 8, 3x + 4y ≤ 12, 2x − 6y < 12 A 4x + 2y ≥ 8, 3x + 4y ≥ 12, 2x − 6y<12 B 4x + 2y ≤ 8, 3x + 4y ≤ 12, 2x − 6y < 12 C - 4x + 2y ≤ 8, 3x + 4y ≥ 12, 2x − 6y < 12 D 4 -6 9 2 :D؟ (6) ما رتبة المصفوفة: 1 0 -3 -5 4×8 C 4×2 A 8x4D 2×4 B 7 أي من الدوال الآتية يكون مداها: {0 = (f(x)| f(x} ؟ وزارة التعليم Ministry of Education 2024-1446 f(x) = [x] A f(x) = |- x + 1 | B f(x) = - | x| C f(x) = -[x] + 1 D Y [ b -5 15 15 25 335 225 30 15 ] C 09 [-6 3 3 ] ^ 9 A 5 -1 8 15 D 9 12 7 -4 2 06 6 4 B 2) أوجد ناتج: 5 [ 3 ] A [ ]10 2 ناتج : [ 3 11 13. إذا كان ذلك ممكنا. ، 8 C 12 6 D الضرب غير معرف [ 11 ] B في أي من الدوال الآتية يكون 0 ) ؟ 8) إذا كان رؤوس ADEF، ذا كان [ 8 ] = x= [ + ] x a b 2 7 c + d وكانت X = Y فإن قيمة ، تساوي: -1 A 2 B -2 C 1 D f(x) = |3x|+1 A f(x) = [3x + 1] B f(x) = |3x| +1 C f(x) = [3x] + 1 D (3 D(−6,2), (4) النقاط (7 ,8) ,5 ,3) ,(6) هي رؤوس احسب مساحة هذا المثلث: 54.5A وحدة مربعة. 60 وحدة مربعة. 58 وحدة مربعة . 61.5 وحدة مربعة. الفصل 2 المصفوفات 104

أسئلة ذات إجابات قصيرة أجب عن كل مما يأتي: (9) هل يوجد للمصفوفة B نظير ضربي؟ فسّر إجابتك. -2 B = [ 33 - 2 ] 6 10) احسب قيمة محددة المصفوفة: (12 72 مع عمر 14 قطعة نقدية من فئة الريال ونصف الريال. فإذا كانت القيمة الكلية لهذه القطع النقدية هي 10.5 ريالات، فاستعمل هذه المعلومات للإجابة عن كل سؤال مما يأتي: افرض أن d تمثل عدد الريالات التي يملكها عمر، و 1 عدد أنصاف الريالات التي يملكها اكتب نظام معادلات يمثل هذه الحالة. ( اكتب معادلة مصفوفية يمكن أن تستعمل لإيجاد قيم كلّ من d و q. حل المعادلة المصفوفية في الفرع b باستعمال النظير الضربي. ما عدد الريالات وأنصاف الريالات التي يملكها عمر؟ 3 1 0 W = 2 5 -4 0 −1 1 (13) مثل بيانيا نظام المتباينات الآتي، ثم حدد رؤوس منطقة الحل وجد القيمة العظمى للدالة المعطاة في منطقة الحل : أسئلة ذات إجابات مطولة أجب عن كل مما يأتي موضحًا خطوات الحل: 11) يستعمل حمد شبكة إحداثيات ليصمم أرضية جديدة في فناء منزله. فإذا كانت الأرضية تمثل حل نظام المتباينات 32 + y = 120, x = 16, y ≥ 0, x ≥ 0, y = - x، وكانت كل وحدة على شبكة الإحداثيات تمثل قدمًا واحدة على الأرض، فما مساحة الأرضية بالقدم المربعة؟ x>0,y> 0 x + 2y < 14 3x+4y≤36 f(x, y) = 8x + 12y (14 صف بالكلمات متى يمكن ضرب مصفوفتين، ومتى لا يمكن ضربهما، وأعط مثالا على ذلك. هل تحتاج إلى مساعدة إضافية؟ إذا لم تستطع حل سؤال... فعد إلى... 14 13 12 11 10 98 765 4 3 2 1 2-3 1-6 2-5 1-5 2-4 2-5 2-1 1-4 2-1 1-5 2-4 1-3 2-3 2-2 وزارة التعليم Ministry of Education الفصل 2 اختبار تراكمي 2105144



































































