نظريتا الباقي والعوامل - رياضيات2-1 - ثاني ثانوي

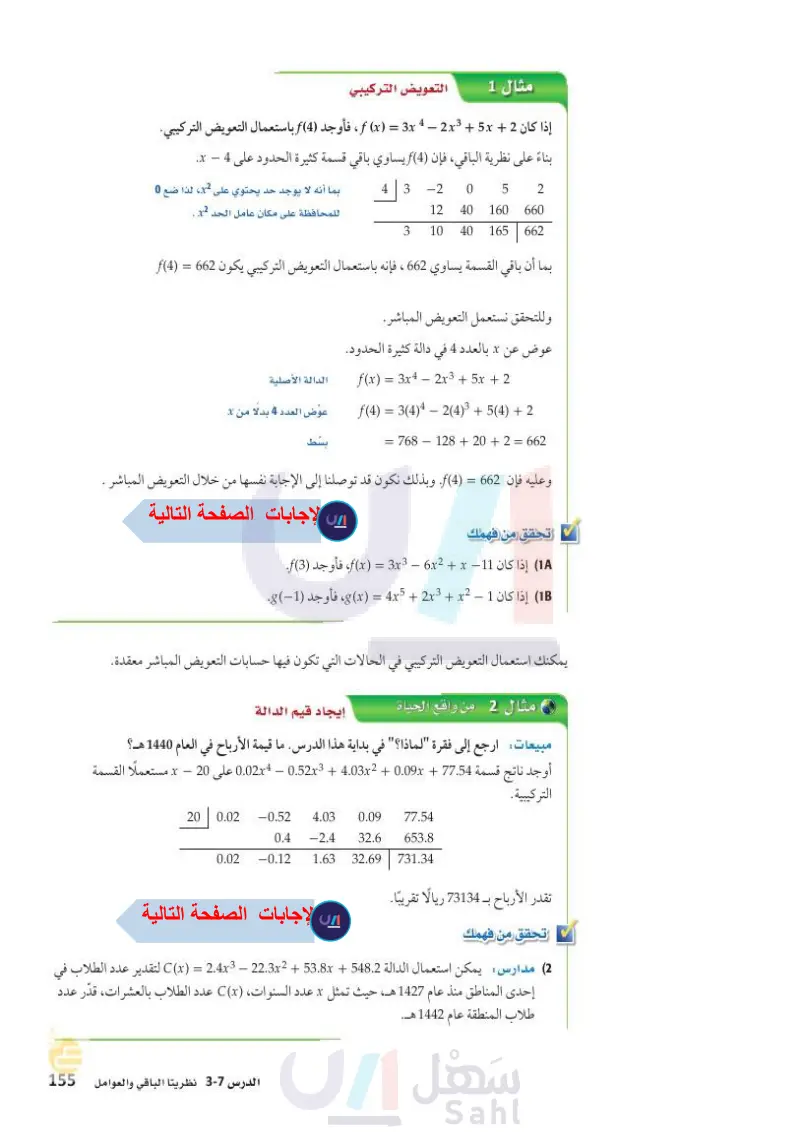
3-7 نظريتا الباقي والعوامل The Remainder and Factor Theorems رابط الدرس الرقمي www.ien.edu.sa فيما سبق درست استعمال خاصية لماذا؟ قدر صاحب بقالة أرباحه السنوية بالدالة: التوزيع والتحليل لتبسيط 77.54 + x) = 0.02x4 - 0.52x3 + 4.03x2 + 0.09x) ، حيث x عدد السنوات منذ العام 1420هـ، وتمثل (x) قيمة الأرباح بمئات الريالات. عبارات جبرية. (الدرس 3 - 3) والآن - أجد قيم الدوال باستعمال التعويض التركيبي - أستعمل التعويض التركيبي لأحدد ما إذا كانت ثنائية حد عاملًا من عوامل كثيرة حدود أم لا . المفردات: نظرية الباقي يمكنك استعمال هذه الدالة لتقدير الأرباح في العام 1440هـ، بإيجاد قيمة الدالة (x) عندما 20 = x، ويمكنك استعمال التعويض التركيبي باعتباره طريقة أخرى للوصول إلى ذلك. التعويض التركيبي : يمكنك إيجاد باقي قسمة دالة كثيرة حدود مثل: 4 + f(x) = −3x2 + 5x على الدالة 3 - x بطريقتين : الطريقة 1: القسمة الطويلة — -3x - 4 3 / 3x2 + 5x + 4 (-)-3x² + 9x (-) -4x + 4 -4x+12 Remainder Theorm 8 التعويض التركيبي الطريقة 2 القسمة التركيبية 3 -3 5 4 -9 -12 X -3 -4 -8 synthetic substitution نظرية العوامل Factor Theorm 154 قارن بين باقي القسمة وهو العدد 8 ، وقيمة (3)f . ƒ(3) = −3(3)² + 5(3) + 4 = −27+ 15 +4 = -8 عوض العدد 3 بدلا من x اضرب بسط لاحظ أن قيمة (3) تساوي باقي قسمة كثيرة الحدود على 3 - x. وهذا يوضّح نظرية الباقي. مفهوم أساسي نظرية الباقي أضف إلى مطويتك التعبير اللفظي إذا قسمت كثيرة حدود ( على X - r ، فإن الباقي ثابت ويساوي (r) ، وكذلك : مثال الباقي المقسوم عليه (x-r) + P(r) ناتج القسمة المقسوم P(x) = Q(x) حيث (X) دالة كثيرة حدود تقل درجتها بواحد عن درجة (x). (x-4) . + (x + 10) 42 x2 + 6x + 2 = إن عملية إيجاد قيمة دالة عند عدد بتطبيق نظرية الباقي واستعمال القسمة التركيبية تسمى التعويض التركيبي. وهي طريقة سهلة لإيجاد قيم دوال كثيرات الحدود، خصوصًا عندما تكون درجة كثيرة الحدود أكبر من الدرجة الثانية. وزارة التعليم الفصل 3 كثيرات الحدود ودوالها Ministry of Education 2024-1446

مثال 1 التعويض التركيبي إذا كان 2 + f ( x ) = 3x 4 - 2x3 + 5x ، فأوجد (4) f باستعمال التعويض التركيبي. بناءً على نظرية الباقي، فإن (4) f يساوي باقي قسمة كثيرة الحدود على 4 - x. 4 -2 3 0 5 2 12 160 40 660 3 10 165 40 662 بما أنه لا يوجد حد يحتوي على x2، لذا ضع 0 للمحافظة على مكان عامل الحد x2 . بما أن باقي القسمة يساوي 662 ، فإنه باستعمال التعويض التركيبي يكون 662 = (4)f وللتحقق نستعمل التعويض المباشر. عوض عن x بالعدد 4 في دالة كثيرة الحدود. f(x) = 3x4 - 2x3 + 5x + 2 f(4) = 3(4)4 — 2(4)³ + 5(4) + 2 - = 768 - 128 +20 +2 = 662 الدالة الأصلية عوض العدد 4 بدلًا من x بسط وعليه فإن 662 = (4) f. وبذلك نكون قد توصلنا إلى الإجابة نفسها من خلال التعويض المباشر . تحقق من فهمك (1) إذا كان 11 f(x) = 3x3 – 6x2 + x، فأوجد (3)f. (1) إذا كان 1 - x) = 4x5 + 2x3 + x2)، فأوجد (1). يمكنك استعمال التعويض التركيبي في الحالات التي تكون فيها حسابات التعويض المباشر معقدة. مثال 2 من واقع الحياة إيجاد قيم الدالة . مبيعات ارجع إلى فقرة "لماذا؟" في بداية هذا الدرس ما قيمة الأرباح في العام 1440هـ ؟ جد ناتج قسمة 77.54 + 0.02x4 – 0.52x3 + 4.03x2 + 0.09x على 20 - x مستعملا القسمة التركيبية. 77.54 653.8 731.34 0.09 4.03 -0.52 0.02 20 32.6 -2.4 0.4 32.69 1.63 -0.12 0.02 تقدر الأرباح بـ 73134 ريالا تقريبًا. تحقق من فهمك (2) مدارس يمكن استعمال الدالة 548.2 + C(x) = 2.4x3 - 22.3x2 + 53.8x لتقدير عدد الطلاب في إحدى المناطق منذ عام 1427هـ، حيث تمثل x عدد السنوات (C(x عدد الطلاب بالعشرات، قدر عدد طلاب المنطقة عام 1442هـ. وزارة التعليم Ministry of Education الدرس - نظريتا الباقي والعوامل 2155144

إرشادات للدراسة عوامل كثيرات الحدود: تبين القسمة التركيبية أدناه أن ناتج قسمة 30 + 2x3 – 3x2 – 17x على 3 + x هو 10 + 2x2 - 9x - 2 -3 -17 -3 30 -6 27 -30 2 -9 10 0 عند قسمة كثيرة حدود على ثنائية حد من عواملها، يكون ناتج القسمة كثيرة حدود تقل درجتها بواحد عن درجة كثيرة الحدود الأصلية. بناءً على عملية القسمة وباستعمال نظرية الباقي فإن : الباقي المقسوم عليه (x + 3) + 0 ناتج القسمة المقسوم 2x3 - 3x2 ― = 17x + 30 (2x2 – 9x + 10) وبما أن باقي القسمة يساوي صفرًا، فإن 0 = (3). و هذا يعني أ أن 3 + x عامل لكثيرة الحدود 30 + 2x3 - 3x2 - 17x . وهذا يوضّح نظرية العوامل التي تعد حالة خاصة من نظرية الباقي. مفهوم أساسي نظرية العوامل 6 تكون ثنائية الحد X - r عاملا من عوامل كثيرة الحدود (x) إذا وفقط إذا كان 0 = (r). يمكنك استعمال نظرية العوامل للتحقق من أن ثنائية حد معينة عامل من عوامل كثيرة حدود معطاة. أضف إلى مطويتك مثال 3 استعمال نظرية العوامل حدد ما إذا كان 5 - x عاملًا من عوامل كثيرة الحدود 15 + P (x) = x3 – 7x2 + x أم لا، ثم أوجد عواملها الأخرى. الخطوة 1 : استعمال نظرية العوامل بناءً على نظرية العوامل تكون ثنائية الحد 5 - x عاملًا من عوامل (x)) إذا كان 0 = (5)P، ولإيجاد (5)P ، يمكنك استعمال التعويض التركيبي. ما 5 1 -7 7 15 5 -10 1-2 -3 -15 0 التحليل إلى العوامل ليس شرطا أن تكون عوامل كثيرة الحدود ثنائيات حد. فمثلاً، عاملا كثيرة الحدود وبما أن باقي القسمة يساوي صفرًا؛ أي أن 0 = (5) ، فإن 5 – x عامل لكثيرة الحدود. الخطوة 2 : تحليل كثيرة الحدود - بما أن 5 - x عامل لكثيرة الحدود؛ لذا يمكن تحليل كثيرة الحدود 15 + x3 – 7x2 + x على النحو الآتي: 3 - 2 - 2 – x). وتكون 3 – x2 – 2x هي كثيرة الحدود الناتجة عن قسمة كثيرة الحدود 15 + x3 + x2 - x هما 15 + x3 – 7x2 + 7x على (5 - x). 3 + x و 5 + 2 - x2 . تحقق مما إذا كانت كثيرة الحدود هذه قابلة للتحليل أم لا. - x2 - 2x - 3 = (x + (1)(x - 3 − 3) حلل ثلاثية الحدود وعليه فإن (3) - ()()()()(5 - x3 – 7x2 + 7x + 15 = (x تحقق : يمكنك التحقق من إجابتك بضرب العوامل ومقارنة كثيرة الحدود الناتجة بكثيرة الحدود الأصلية. تحقق من فهمك (3) حدد ما إذا كان 2 - x عاملا من عوامل كثيرة الحدود 12 + x3 x 2 + x أم لا، ثم أوجد عواملها الأخرى عليم 156 الفصل 3 كثيرات الحدود ودوالها Ministry of Education 2024-1446

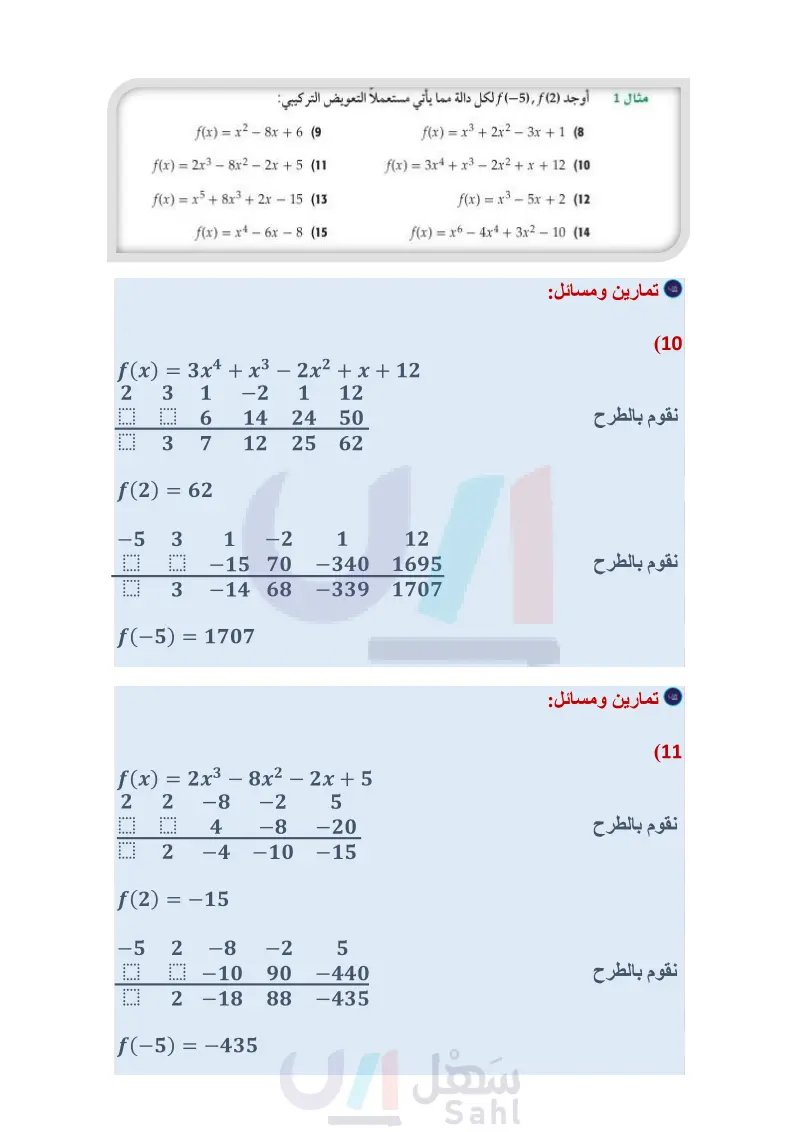
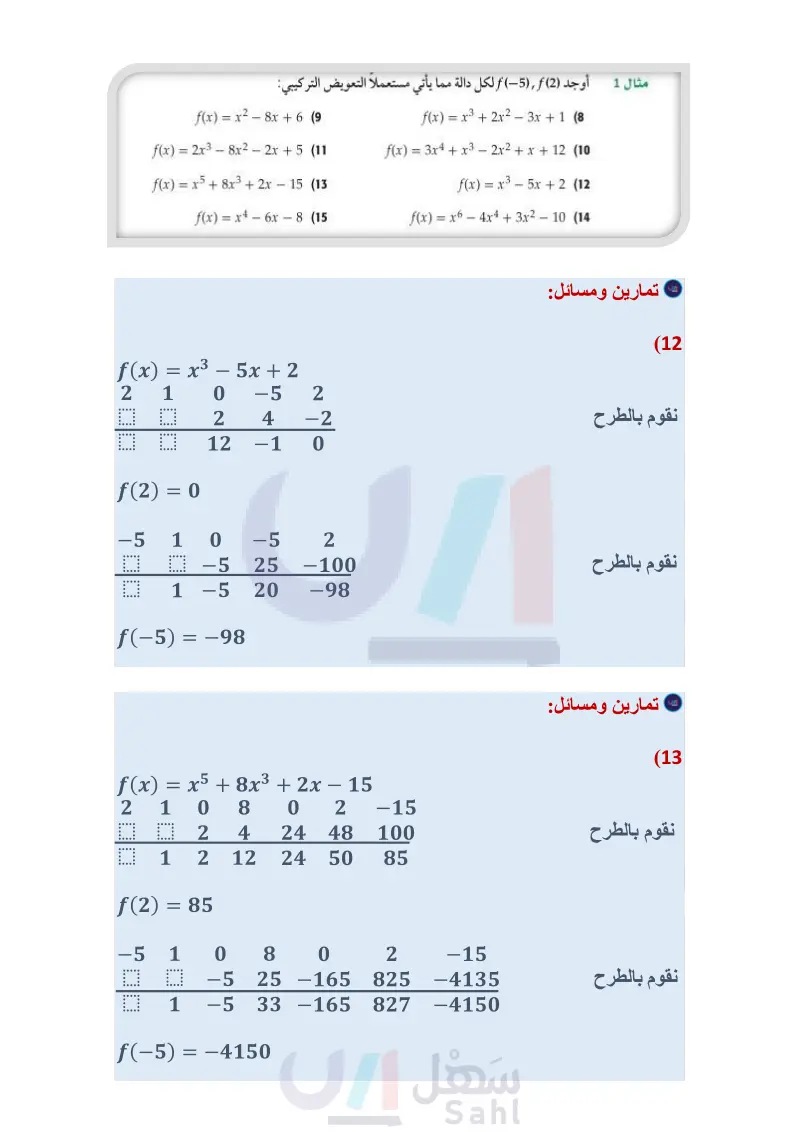
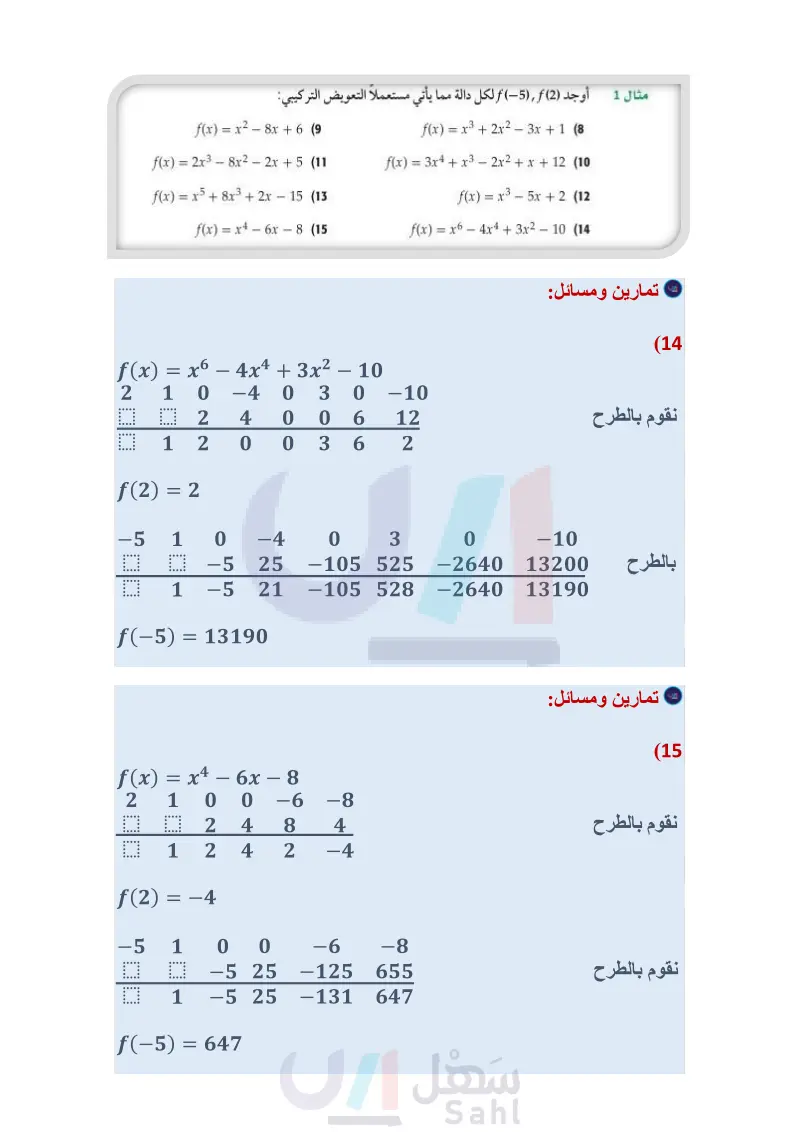
تأكد أوجد (2), (4) لكلِّ من الدالتين الآتيتين مستعملا التعويض التركيبي: مثال 1 f(x) = 2x3 – 5x2 - x + 14 (1 - f(x) = x4 + 8x3 + x2 - 4x - 10 (2) 3 جوارح يمكن تمثيل عدد أزواج النسور في محمية باستعمال الدالة مثال 2 1147.97 + x) = -0.16x3 + 15.83x2 - 154.15x) حيث x عدد السنوات منذ عام 1390هـ، فما العدد التقريبي المتوقع لأزواج هذه النسور في عام 1443 هـ ؟ في كل مما يأتي كثيرة حدود ودالة من الدرجة الأولى، حدد ما إذا كانت هذه الدالة عاملًا من عوامل كثيرة الحدود مثال 3 لا، ثم أوجد عواملها الأخرى: أم : تمارين ومسائل x3 + x2 - 16x - 16; x + 1 (5 2x3 - 5x2 - 28x + 15; x + 3 (7) x3 - 6x2 + 11x - 6; x - 1 (4) 3x3 + 10x2 - x - 12; x - 1 (6) أوجد (2) f (5), f لكل دالة مما يأتي مستعملاً التعويض التركيبي: مثال 1 f(x) = x2 - 8x + 6 (9) f(x) = 2x3 - 8x2 - 2x + 5 (11 f(x) = x5 + 8x3 + 2x - 15 (13) - f(x) = x4 - 6x - 8 (15 f(x) = x3 + 2x2 - 3x + 1 (8 f(x) = 3x4 + x3 - 2x2 + x + 12 (10 f(x) = x3 - 5x + 2 (12 f(x) = x6 - 4x4 + 3x2 - 10 14 (16 وقود يقدر استهلاك سيارة للوقود (بالميل لكل جالون وفقًا للدالة مثال 2 0.38 - f(x) = 0.00000056x4 - 0.000018x3 - 0.016x2 + 1.38x ، حيث x سرعة السيارة بالأميال لكل ساعة. حدد استهلاك السيارة للوقود إذا سارت بالسرعات الآتية 40mi/h, 50mi/h, mih. في كل مما يأتي كثيرة حدود ودالة من الدرجة الأولى. حدد ما إذا كانت هذه الدالة عاملًا من عوامل كثيرة الحدود مثال 3 أم لا، ثم أوجد عواملها الأخرى: x4 + 2x3 - 8x - 16; x + 2 (18 x3 - x2 - 5x - 3; x - 3 (20 2x3 + 7x2 - 53x - 28; x - 4 (22) x3 + 2x2 - x - 2; x + 2 (24 16x5 - 32x4 - 81x + 162; 2x - 3 (26) x3 - 3x + 2; x + 2 (17 x3 - x2 - 10x - 8; x + 2 (19) 2x3 + 17x2 + 23x - 42; x - 1 (21 x4 + 2x3 + 2x2 - 2x - 3; x - 1 (23 6x3 - 25x2 + 2x + 8; 2x + 1 (25) (27) زوارق تحرك زورق بخاري من السكون في اتجاه معاكس للأمواج، فإذا كانت سرعته بالأقدام لكل ثانية تعطى بالدالة f(t) = 0.04t4 + 0.8t3 + 0.5t 2 - t ، حيث الزمن بالثواني. أوجد سرعة الزورق بعد مرور زمن: 1 ووضّح إذا استغرق الزورق 6s ليقطع المسافة بين عوامتين، فأوجد (6)f مستعملاً التعويض التركيبي، ووف وزارة التعليم ماذا يعني ذلك. Ministry of Education الدرس - نظريتا الباقي والعوامل 2157144

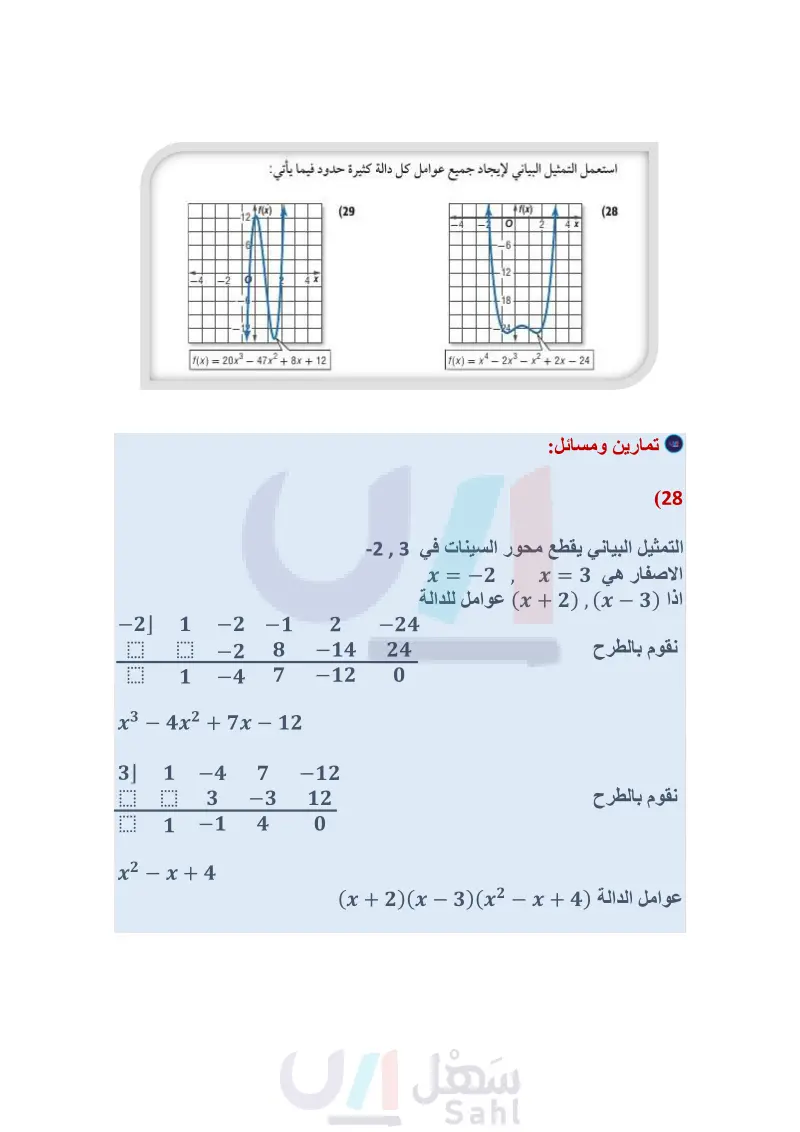
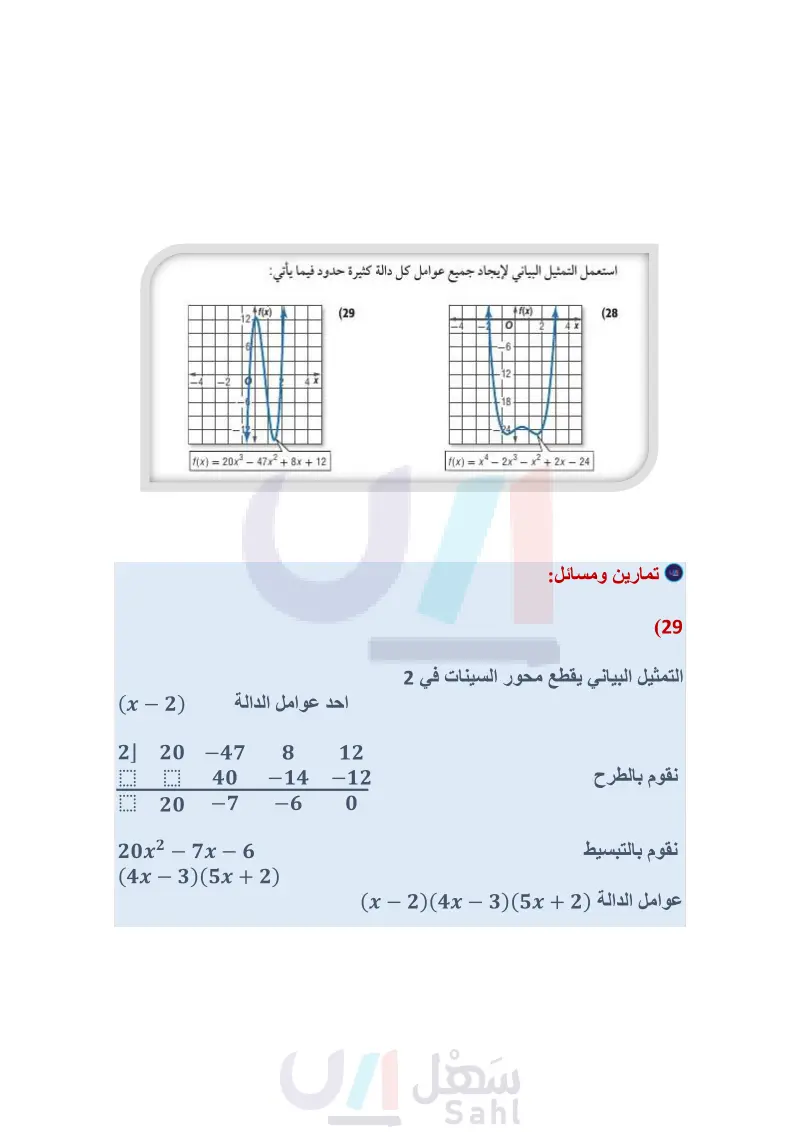
-4 -2 f(x) 12 6 استعمل التمثيل البياني لإيجاد جميع عوامل كل دالة كثيرة حدود فيما يأتي: 4X -12- f(x) = 20x3 - 47x 2 + x + 12 (29 f(x) (28 -4 2 4 x -6 -12 -18 24 | f(x) = x1 - 2x3 - x2 + 2x - 24 تمثيلات متعددة لتكن الدالة : f(x) = x4 - 4x2 . (30 ( جبريًا : إذا كان 2 - x عاملاً من عوامل هذه الدالة، فأوجد كثيرة الحدود الناتجة عن قسمة هذه الدالة على (2 - x). b : (6) جدوليًا كوّن جدول قيم لكثيرة الحدود التي وجدتها في الفرع "a" حيث 2,10,12 x. تحليليا : اعتمادًا على جدول القيم الذي كوّنته، ما الاستنتاجات التي يمكن أن نتوصل إليها حول بقية عوامل الدالة: f(x) = x4 4x2؟ وضح إجابتك. بيانيا : مثل الدالة الأصلية بيانيًا لتؤكد الاستنتاجات التي توصلت إليها. أوجد قيم التي تجعل باقي القسمة في كل مما يأتي يساوي 3: تنبيه التعويض التركيبي تذكر أنه في التعويض التركيبي يتم قسمة كثيرة حدود على ثنائية حد على الصورة ( - ). وفي هذه الحالة استعمل ه، وإذا كانت ثنائية الحد على الصورة ) فاستعمل ه - . (x² - x + k) ÷ (x − 1) (31 - (x2+5x+7): (x − k) (33 - مسائل مهارات التفكير العليا (x2 + kx - 17) : (x - 2) (32 (x3 + 4x 2 + x + (k) : (x + (2) (34) (35) تبرير: إذا قسمت دالة كثيرة الحدود (f(x على x - c ، فماذا يمكن أن تستنتج إذا كان: (a) الباقي يساوي صفرًا؟ b) الباقي يساوي 1؟ ناتج القسمة يساوي 1 والباقي يساوي صفرًا؟ (36) مسألة مفتوحة : اكتب دالة تكعيبية يكون باقي قسمتها على 2 - x يساوي ،8، وباقي قسمتها على 3 - x يساوي 5-. (37) اكتب وضّح لماذا تعد نظرية العوامل حالة خاصة من نظرية الباقي؟ وزارة التعليم Ministry of Education 2024-1446 الفصل 3 كثيرات الحدود ودوالها 158

تدريب على اختبار (38) أي مما يأتي هو تحليل للعبارة 27x3 + y3 ؟ (39) ما حاصل ضرب العددين المركبين (1 - 4 - 4) 17 C 15 A 17 - 8i D 16 - i B وزارة التعليم Ministry of Education الدرس 37 نظريتا الباقي والعوامل 2159144 (3x + y)(3x + y)(3x + y) (3x + y)(9x² - 3xy + y²) B (3x − y)(9x² + 3xy + y²) C - (3x − y)(9x² + 9xy + y²) D - مراجعة تراكمية حُلَّ كلَّ معادلة مما يأتي: (الدرس (2-3) x4 - 4x2 - 21 = 0 40 x46x227 (41 4x48x296 = 0 (42 حُلَّ كلًّا من النظامين الآتيين بيانيا: (مهارة سابقة) y=3x-1 (43 y=-2x+4 3x+2y=8 (44 -4x+6y=11 إذا كان 4 + x) = x2 - 2x, d(x) = 3x2 - 6x)، فأوجد قيمة كل مما يأتي: (الدرس (3-3) c(a + 2) — d(a — 4) (45 c(a-3)+d(a+1) (46 c(-3a)+d(a + 4) (47 3d (3a)-2c(-a) (48 c(a)+5d (2a) (49 -2d (2a+3)-4c (a² + 1) (50