دوال خاصة - رياضيات2-1 - ثاني ثانوي
الفصل الأول: الدوال والمتباينات
الفصل الثاني: المصفوفات
الفصل الثالث: كثيرات الحدود ودوالها
نشاط الفصل الأول: الدوال والمتباينات
نشاط الفصل الثاني: المصفوفات
نشاط الفصل الثالث: كثيرات الحدود ودوالها
رابط الدرس الرقمي www.ien.edu.sa دوال خاصة Special Functions 1-3 فيما سبق: لماذا؟ درست حل معادلات تتضمن السمنة حالة مرضية يمكن تعريفها طبيا أنها زيادة القيمة المطلقة. (مهارة سابقة) والآن : أكتب الدوال المتعددة التعريف وأمثلها بيانيا أكتب الدوال الدرجية أخذ مقدار الدهون في الجسم، وتنتج السمنة عن طاقة أكبر من حاجة الجسم دون استهلاكها. ويبين الجدول المجاور نسب المصابات بالسمنة لفئات عمرية مختلفة في المملكة. نسب المصابات بالسمنة في المملكة حسب الفئة العمرية من إلى النسبة 19% 24 15 38% 34 25 53% 44 35 58% 54 45 49% 64 55 المصدر: مسح المعلومات الصحية في المملكة وزارة الصحة، 1435هـ الدالة المتعددة التعريف الدالة التي تربط بين العمر ونسبة المصابات بالسمنة ليست خطية؛ لأن كل فترة ودوال القيمة المطلقة من مجال الدالة معرفة بعبارة مختلفة، فالدالة التي تكتب باستعمال عبارتين أو أكثر تسمى دالة متعددة التعريف. وعند تمثيل الدالة المتعددة التعريف بيانياً توضع دائرة صغيرة مظللة عند الطرف لتشير إلى أن النقطة تنتمي إلى التمثيل البياني، وتوضع دائرة غير مظللة لتشير إلى أن النقطة لا تنتمي إلى التمثيل البياني. وأمثلها بيانيًا. المفردات: الدالة المتعددة التعريف piecewise-defined function الدالة المتعددة التعريف الخطية piecewise-linear function مثال 1 مثل الدالة تمثيل الدالة متعددة التعريف 2 x < -1 x 2 -1 - x x + 3 } = (f(x بيانيًا. ثم حدد كلا من مجالها ومداها. الخطوة 1 مثل 2 - f(x) = x بيانيًّا عندما 1- > x . O X احسب قيمة المقدار 2 x عندما -1 = x ، وعند قيمة أخرى لـ x أقل من 1 ولتكن 2 - f(x) = x -2 f(-2)=(-2)-2 = -4 f(x) = x -2 f(1) = (-1) - 2 = -3 حدد النقطتين (24) (13) وصل بينهما بنصف مستقيم وبما أن العدد -1 لا يحقق المتباينة لذا نبدأ بدائرة غير مظللة عند النقطة (3-1). الخطوة 2 مثل 3 + f(x) = x بيانيا عندما 1- = x . احسب قيمة المقدار 3 + x عندما -1 = x ، وعند قيمة أخرى لـ x أكبر من 1 ولتكن 0 f(x) = x + 3 f(0) = (0) + 3 = 3 f(x) = x + 3 f(-1) = (-1) + 3 = 2 حدد النقطتين (0) (1) وصل بينهما بنصف مستقيم. وبما أن العدد -1 يحقق المتباينة، لذا نبدأ بدائرة مظللة عند النقطة (1) وبما أن الدالة معرّفة عند جميع قيم ، لذا فالمجال هو مجموع هو مجموعة الأعداد الحقيقية. قيم (f(x للأزواج المرتبة في التمثيل البياني للدالة هي جميع الأعداد الحقيقية الأقل من 3- وكل الأعداد الحقيقية الأكبر من أو تساوي ،2 ، لذا فإن المدى هو 2 < (f(x أو 3- > (f(x) | f(x } تحقق من فهمك وزارة التعليم Ministry of Education الدرس 3-1 دوال خاصة 1 - 225 . f(x) = X 1 x + 2 ,x < 0 (1 ,x> 0 الدالة الدرجية step function دالة أكبر عدد صحيح greatest integer function دالة القيمة المطلقة absolute value function

إرشادات للدراسة تمثيل الدوال المتعددة التعريف بيانيا تمثل الدوال المتعددة التعريف غالبًا بعدة دوال خطية. وتسمى حينئذ الدالة المتعددة التعريف الخطية . مثال 2 كتابة الدالة المتعددة التعريف اكتب الدالة المتعددة التعريف الممثلة بيانيا في الشكل المجاور. قد تكون الدوال المتعددة اكتب الدالة التي تمثل كل جزء في التمثيل البياني. التعريف متصلة أو غير الجزء الأيسر يمر بالنقطتين (1),(3) ، وميله 22 متصلة. -1-3 -2-0 f(x) 543NT 1 ‹ = -4-3-20 1 2 3 4x وباستعمال صيغة الميل ونقطة مثلا، فإن هذا الجزء تمثله الدالة 3 + f(x) - 3 = 2x - (0) ، f(x) = 2x) ، ولوجود دائرة غير مظللة عند النقطة (15)، فإن هذا يعني أن الدالة معرّفة على الفترة {1 > xx}. ― وبالطريقة نفسها فإن الجزء الأوسط تمثله الدالة 2 + f(x) = x . که ما -3 وتوجد دائرتان مظللتان عند النقطتين (11) و (20)، وهذا يعني أن الدالة معرّفة على الفترة {2 = x1 = x}. كذلك الجزء الأيمن تمثله الدالة 3 = (f(x . وتوجد دائرة غير مظللة عند النقطة (23). وهذا يعني أن الدالة معرفة على الفترة 2 < xx، ونكتب الدالة المتعددة التعريف على النحو الآتي: f(x)=3 2x + 3, x < 1 -x+2, 1<x<2 3, x>2 تحقق يبين التمثيل البياني نصف مستقیم میله موجب عندما تكون 1 > x. ويبين أيضًا قطعة مستقيمة ميلها سالب عندما تكون 2 = x = 1 ونصف مستقیم آخر میله صفر عندما تكون 2 < x. لذا يكون تعريف الدالة منطقيًّا للتمثيل البياني المعطى. f(x) -8- + مح -8- 4 12x تحقق من فهمك (2) اكتب الدالة المتعددة التعريف الممثلة بيانيا في الشكل المجاور. الدالة الدرجية من الدوال المتعددة التعريف الخطية الشهيرة الدالة الدرجية التي تتكون من قطع مستقيمة أفقية، وقد سُميت بهذا الاسم لأن تمثيلها البياني يشبه الدرج، كما أن دالة أكبر عدد صحيح التي تكتب على الصورة [f(x) = [x، هي مثال على الدالة الدرجية؛ حيث يعني الرمز [x] أكبر عدد صحيح أقل من أو يساوي x. فعلى سبيل المثال : 3 = [3.25] وكذلك 5- = [4.6]. مفهوم أساسي دالة أكبر عدد صحيح الدالة الرئيسة (الأم) : [f(x) = [x ، وتُعرّف على النحو التالي: أضف إلى مطويتك f(x) -3- f(x) = [x] 432T -2- -4-3-201 ... وزارة التعليم Ministry of Education 2024-1446 : -1 -1 < x < 0 f(x) = 0 0 < x <1 1 1≤ x < 2 2 2 ≤ x ≤ 3 234x : Do 234 المجال : شكل التمثيل البياني: قطع مستقيمة أفقية. مجموعة الأعداد الحقيقية المدى المقطعان : مجموعة الأعداد الصحيحة 0 = (f(x حيث 1 > x = 0 ,0 ≤ x الفصل 1 الدوال والمتباينات 26

تمثيل الدوال المتعددة التعريف بيانياً
إرشادات للدراسة تمثيل الدوال المتعددة التعريف بيانيا تمثل الدوال المتعددة التعريف غالبًا بعدة دوال خطية. وتسمى حينئذ الدالة المتعددة التعريف الخطية . مثال 2 كتابة الدالة المتعددة التعريف اكتب الدالة المتعددة التعريف الممثلة بيانيا في الشكل المجاور. قد تكون الدوال المتعددة اكتب الدالة التي تمثل كل جزء في التمثيل البياني. التعريف متصلة أو غير الجزء الأيسر يمر بالنقطتين (1),(3) ، وميله 22 متصلة. -1-3 -2-0 f(x) 543NT 1 ‹ = -4-3-20 1 2 3 4x وباستعمال صيغة الميل ونقطة مثلا، فإن هذا الجزء تمثله الدالة 3 + f(x) - 3 = 2x - (0) ، f(x) = 2x) ، ولوجود دائرة غير مظللة عند النقطة (15)، فإن هذا يعني أن الدالة معرّفة على الفترة {1 > xx}. ― وبالطريقة نفسها فإن الجزء الأوسط تمثله الدالة 2 + f(x) = x . که ما -3 وتوجد دائرتان مظللتان عند النقطتين (11) و (20)، وهذا يعني أن الدالة معرّفة على الفترة {2 = x1 = x}. كذلك الجزء الأيمن تمثله الدالة 3 = (f(x . وتوجد دائرة غير مظللة عند النقطة (23). وهذا يعني أن الدالة معرفة على الفترة 2 < xx، ونكتب الدالة المتعددة التعريف على النحو الآتي: f(x)=3 2x + 3, x < 1 -x+2, 1<x<2 3, x>2 تحقق يبين التمثيل البياني نصف مستقیم میله موجب عندما تكون 1 > x. ويبين أيضًا قطعة مستقيمة ميلها سالب عندما تكون 2 = x = 1 ونصف مستقیم آخر میله صفر عندما تكون 2 < x. لذا يكون تعريف الدالة منطقيًّا للتمثيل البياني المعطى. f(x) -8- + مح -8- 4 12x تحقق من فهمك (2) اكتب الدالة المتعددة التعريف الممثلة بيانيا في الشكل المجاور. الدالة الدرجية من الدوال المتعددة التعريف الخطية الشهيرة الدالة الدرجية التي تتكون من قطع مستقيمة أفقية، وقد سُميت بهذا الاسم لأن تمثيلها البياني يشبه الدرج، كما أن دالة أكبر عدد صحيح التي تكتب على الصورة [f(x) = [x، هي مثال على الدالة الدرجية؛ حيث يعني الرمز [x] أكبر عدد صحيح أقل من أو يساوي x. فعلى سبيل المثال : 3 = [3.25] وكذلك 5- = [4.6]. مفهوم أساسي دالة أكبر عدد صحيح الدالة الرئيسة (الأم) : [f(x) = [x ، وتُعرّف على النحو التالي: أضف إلى مطويتك f(x) -3- f(x) = [x] 432T -2- -4-3-201 ... وزارة التعليم Ministry of Education 2024-1446 : -1 -1 < x < 0 f(x) = 0 0 < x <1 1 1≤ x < 2 2 2 ≤ x ≤ 3 234x : Do 234 المجال : شكل التمثيل البياني: قطع مستقيمة أفقية. مجموعة الأعداد الحقيقية المدى المقطعان : مجموعة الأعداد الصحيحة 0 = (f(x حيث 1 > x = 0 ,0 ≤ x الفصل 1 الدوال والمتباينات 26

تدفع شركة لإعادة تدوير الورق 25 ريالا عن كل صندوق من الورق اكتب الدالة التي تمثل هذا الموقف ومثلها بيانيا.


تقدر مخلفات الورقية في السعودية بـ 1.5 مليون طن سنويا .
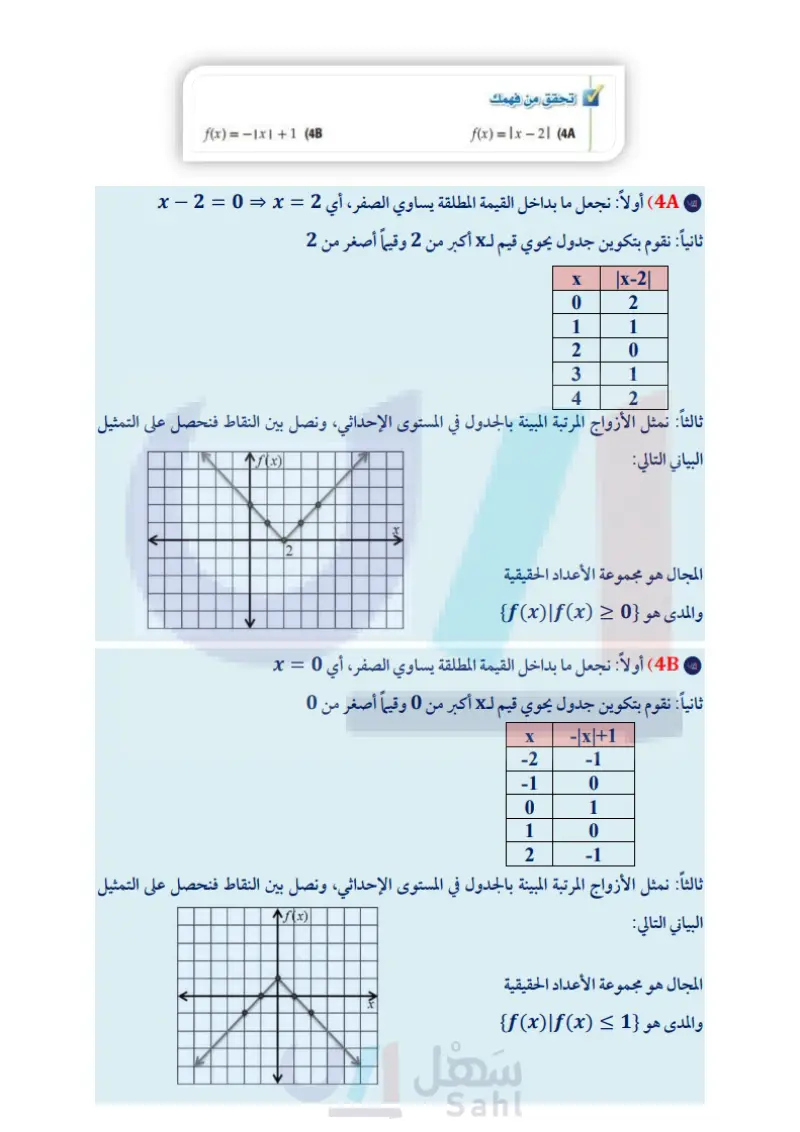
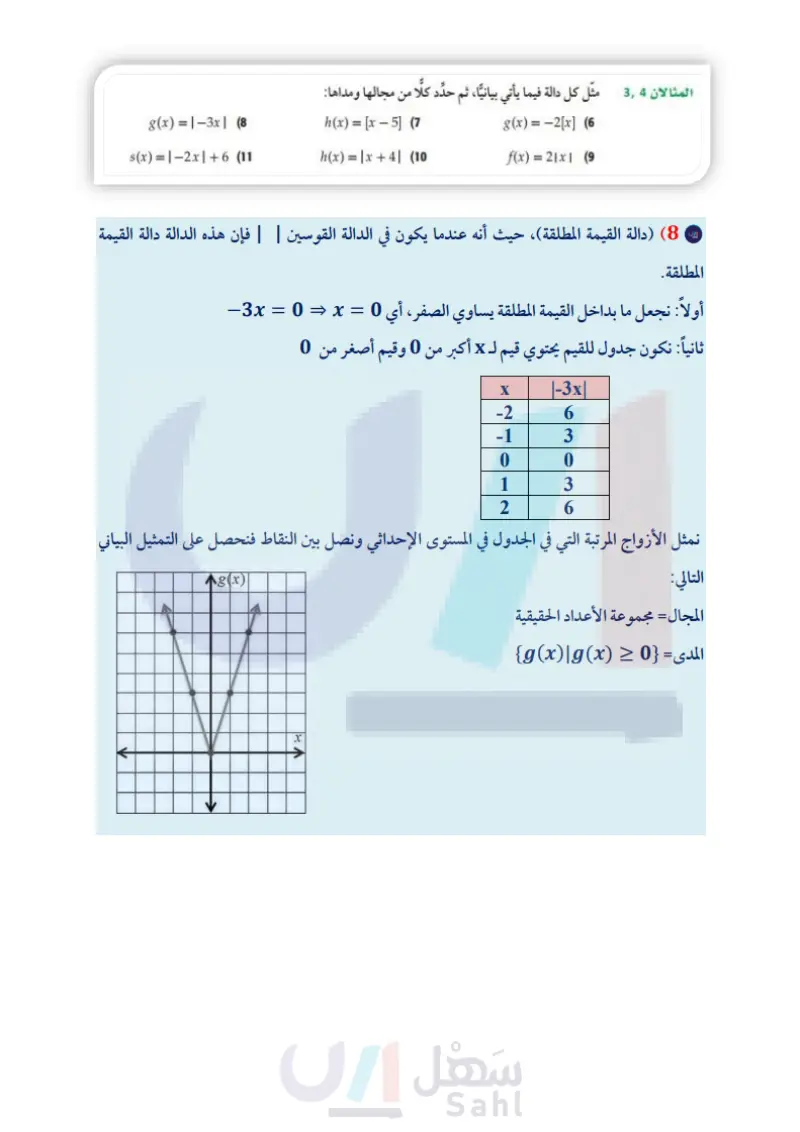
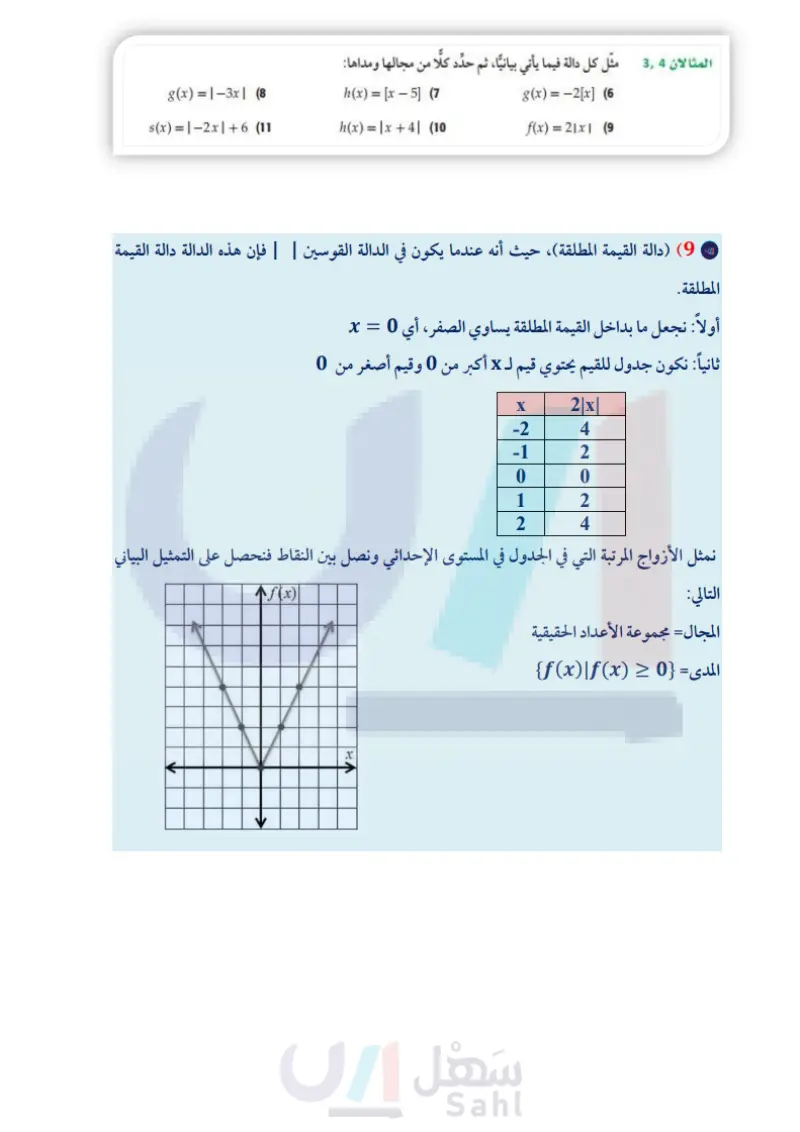
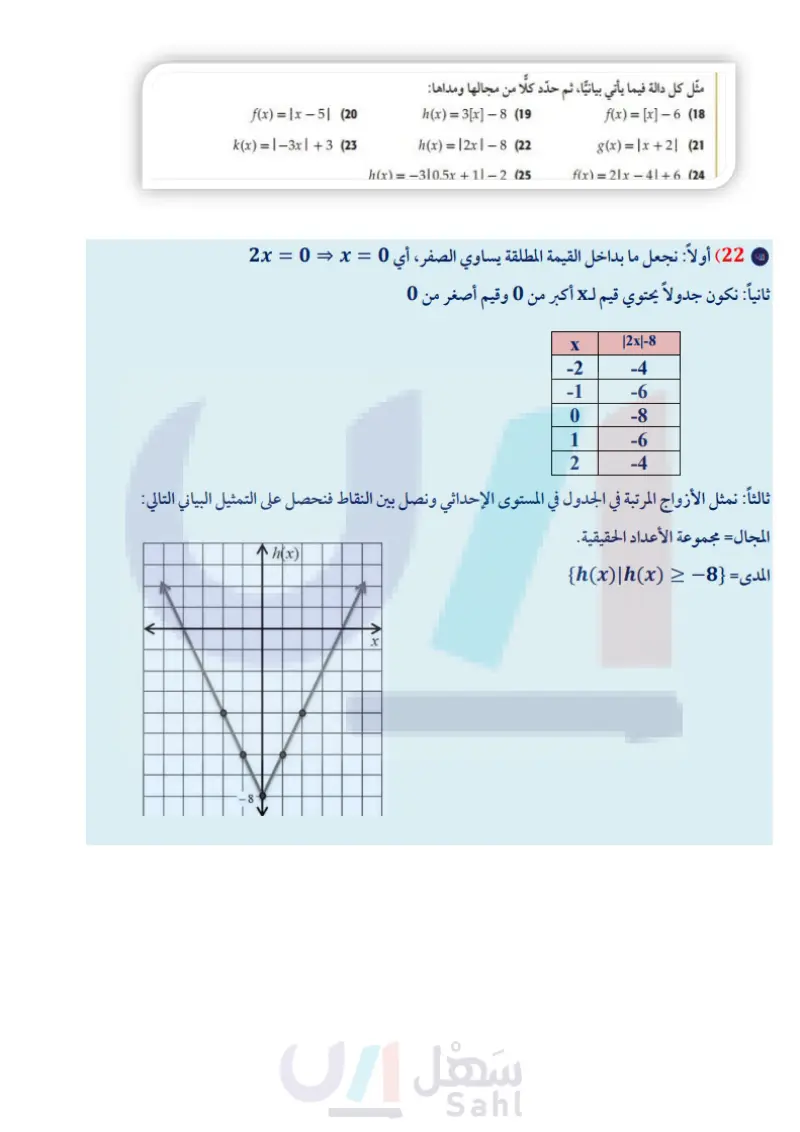
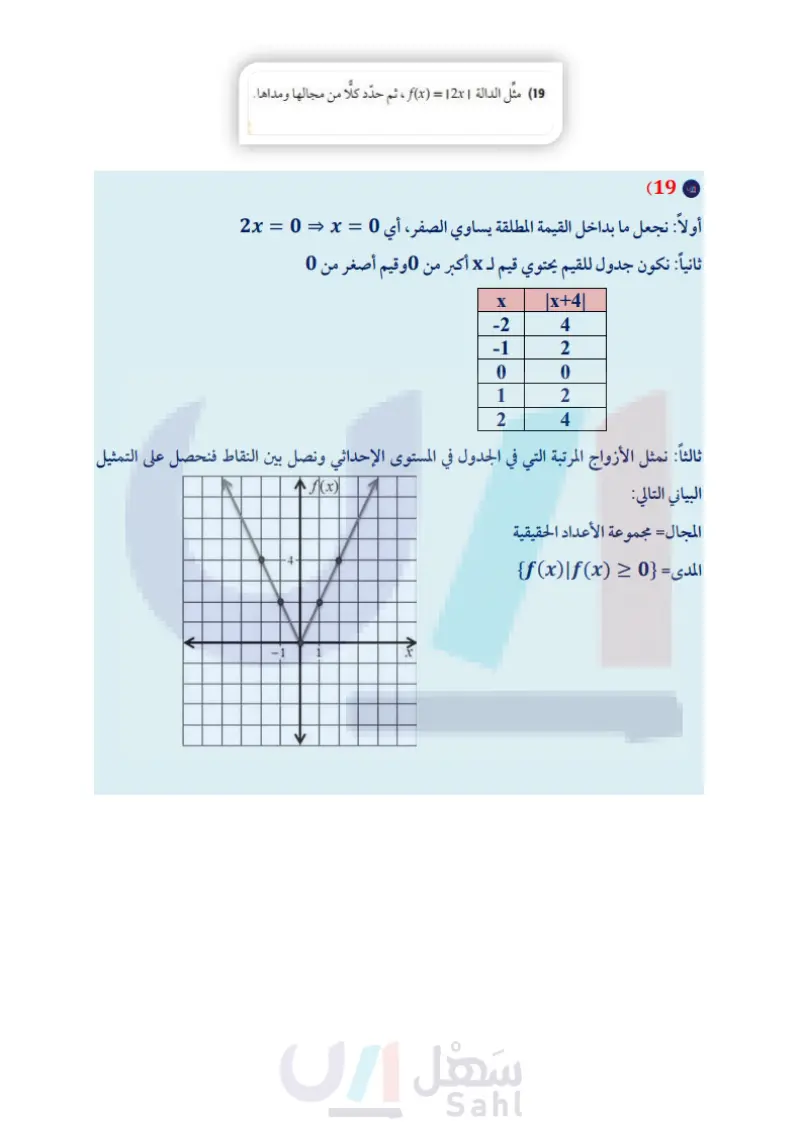
مثال 4 دالة القيمة المطلقة مثل الدالة 4 - f(x) = 12x1 بيانيا، ثم حدد كلًا من مجالها ومداها. (1) اجعل ما بداخل القيمة المطلقة يساوي الصفر | (3 مثل الأزواج المرتبة في المستوى الإحداثي. أي 0 = 2x أو 0 = x (2) كوّن جدولا للقيم، يحوي قيمًا لـ x أكبر من 0 (4) صل بين النقاط. +f(x) O 2 X المجال هو مجموعة الأعداد الحقيقية، والمدى •{f(x)|f(x) ≥ −4} es وقيمًا أصغر من 0 X |2x|-4 -2 0 −1 -2 0 -4 1 -2 2 0 تحقق من فهمك f(x) = - |x | + 1 (4B f(x) =|x2| (4A مثال 1 مثل كل دالة مما يأتي بيانيًا، ثم حدد كلًا من مجالها ومداها: x ≤ −1 -1 < x <4 (2 -3, x ≤-4 f(x) = X, -x+6, -4<x<2 x≥2 (1 8, 2x f(x)= -4-x, x > 4 مثال 2 اكتب الدالة المتعددة التعريف الممثلة بيانيًا في كل مما يأتي: g(x) (4 8 6 4 2 -8- 6- -2- -8-6-4-20 2 4 6 8 x -4 -6 -8 46% 88 y 02- +2 4- -8-6-4-20 2 4 6 8 x -4- -6 -8 (3 تأكد مثال 3 (5) محاضرات طبية : يريد أحد الأطباء إلقاء محاضرة حول العدوى في قاعة تتسع لـ 250 شخصًا فقط، وكان عدد راغبي حضور المحاضرة أكثر من ذلك بكثير. مثل بيانيا دالة متعددة التعريف تبين العلاقة بين عدد المحاضرات لا التي يمكن أن يلقيها الطبيب، وعدد الحضور x. المثالان 34 مثل كل دالة فيما يأتي بيانيًا، ثم حدد كلًا من مجالها ومداها: g(x)=-3x| (8 s(x)=-2x+6 (11 h(x) = [x-5] (7 h(x) = | x + 4 | (10 وزارة التعليم Ministry of Education 2024-1446 g(x) = −2[x] (6 f(x)=2|x| (9 الفصل 1 الدوال والمتباينات 28

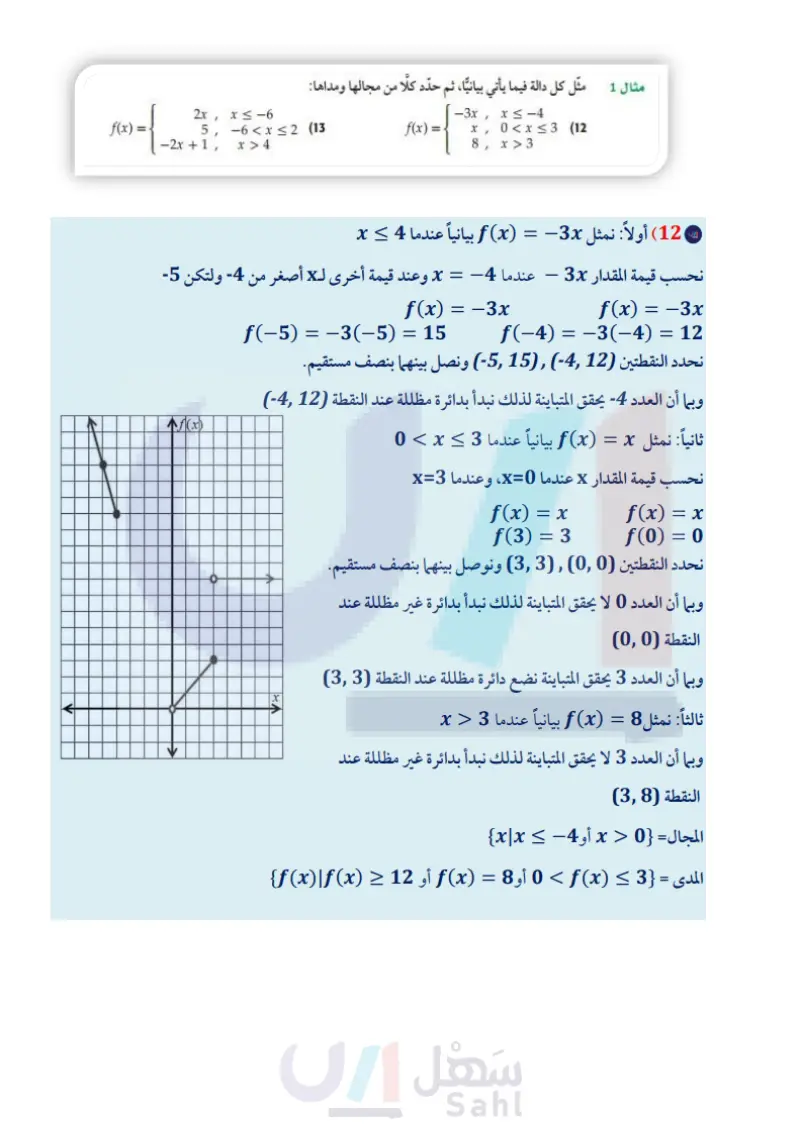
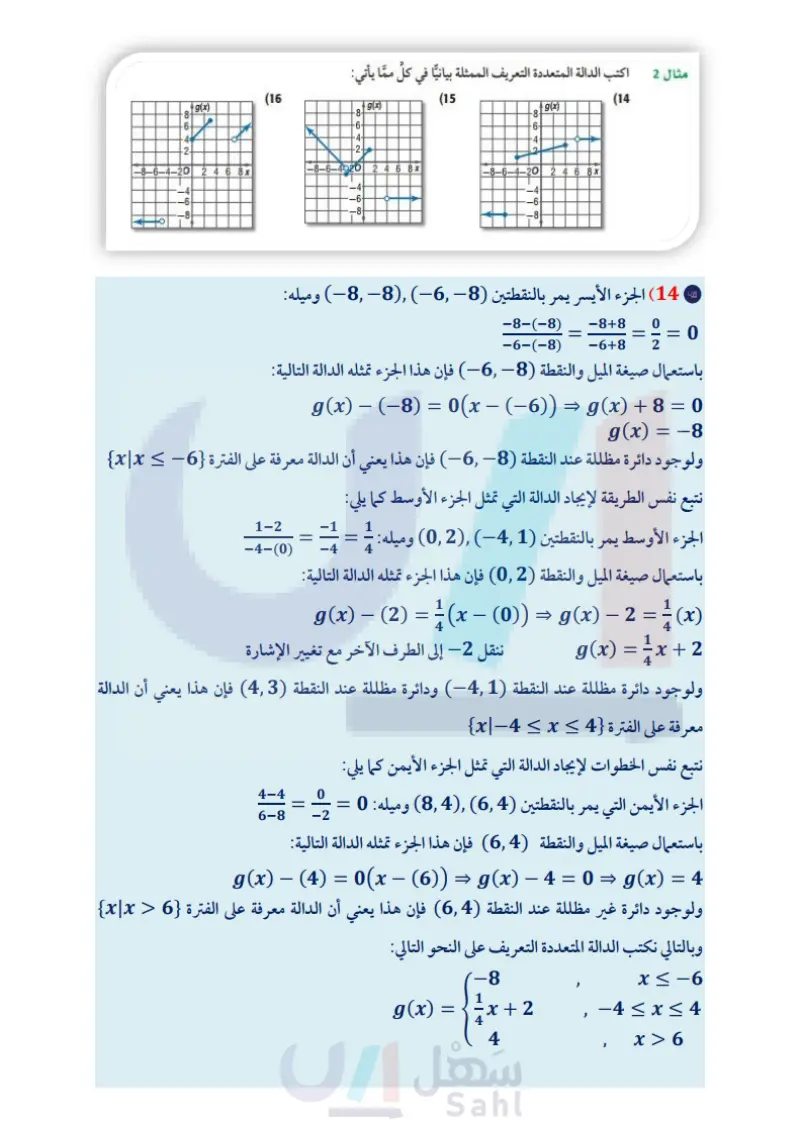
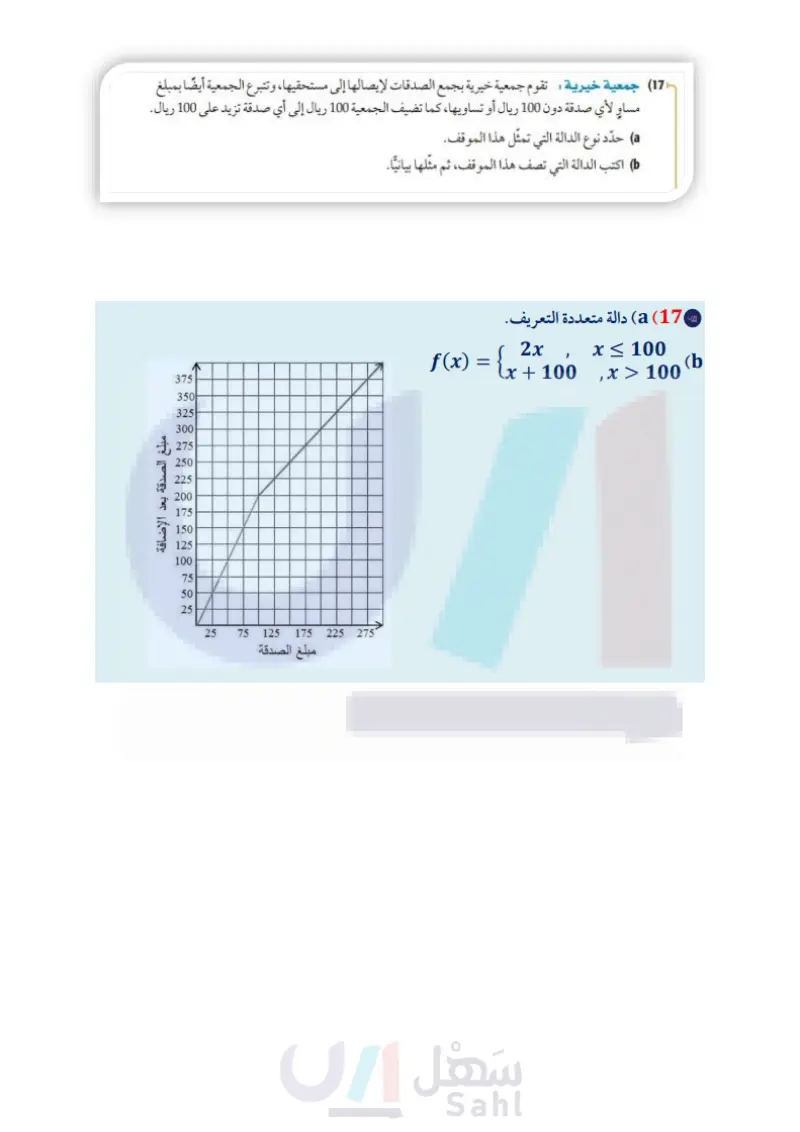
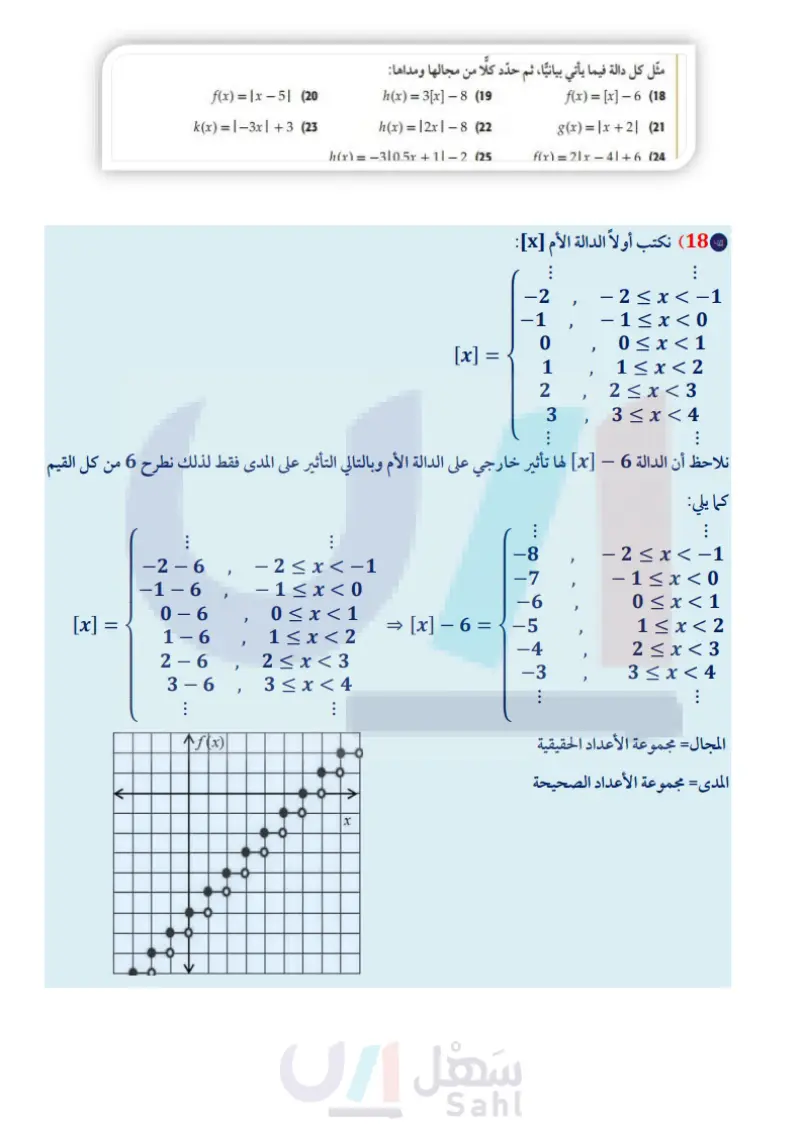
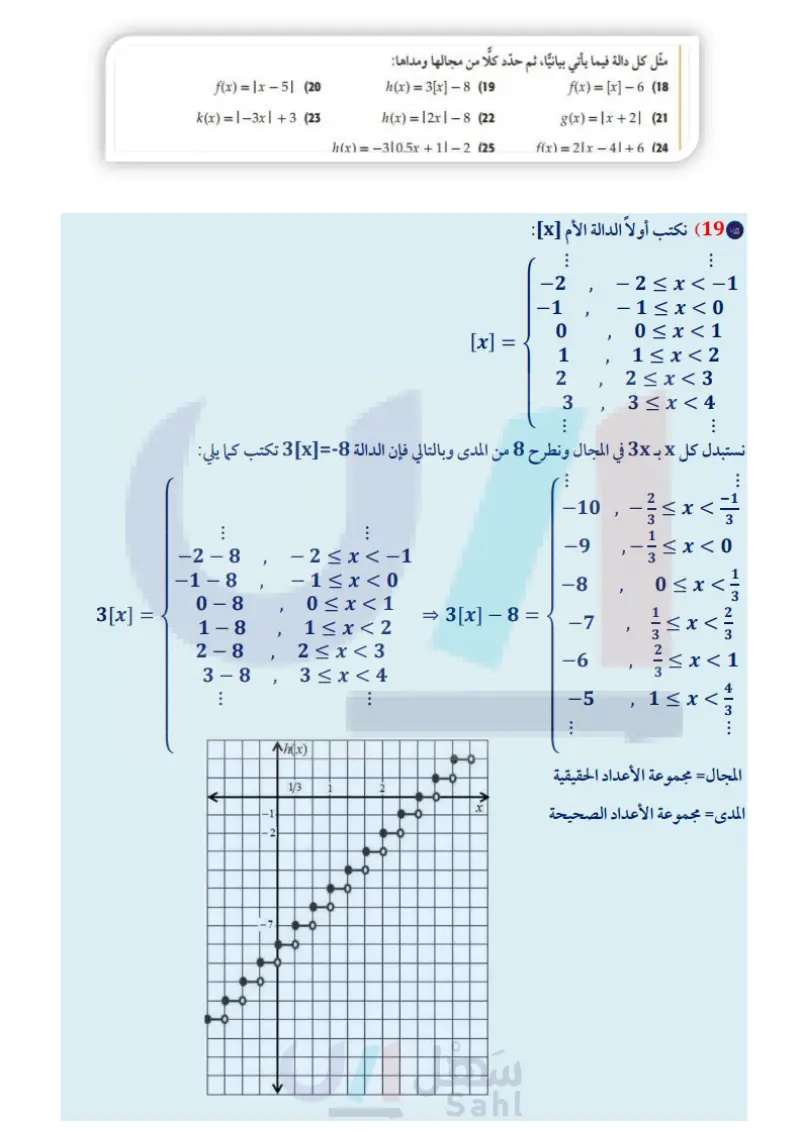
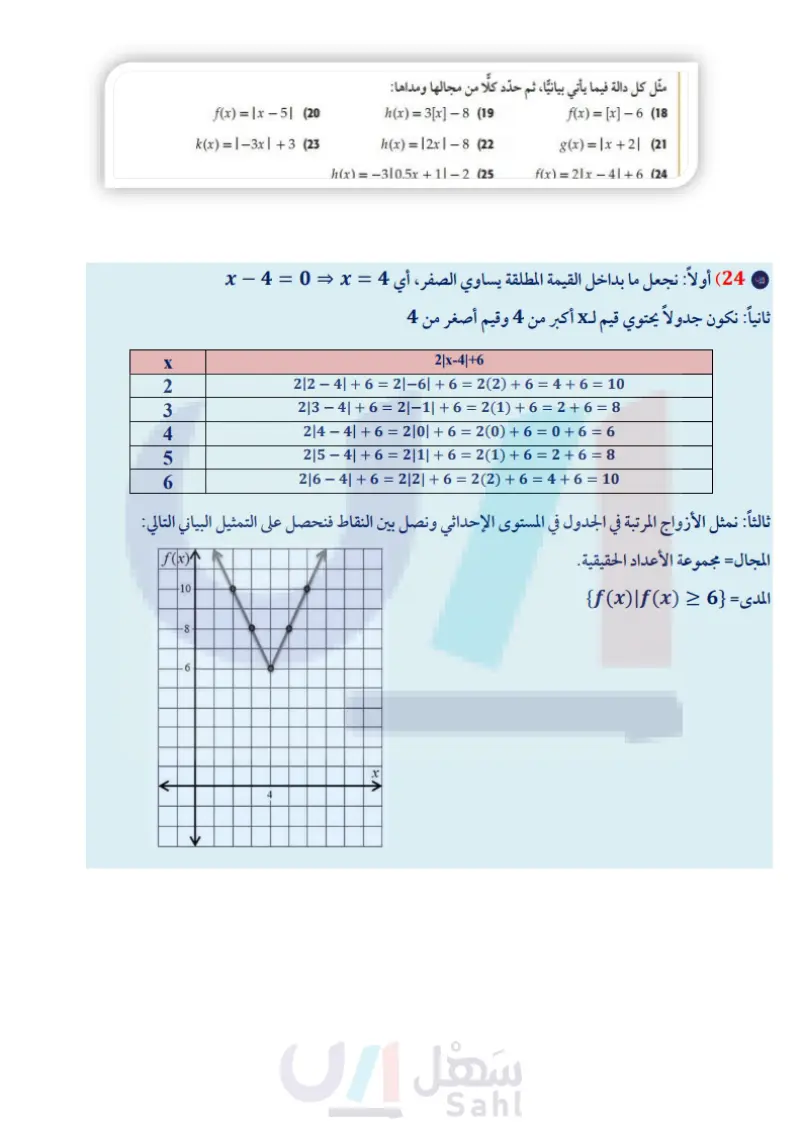
تدرب وحل المسائل مثال 1 مثل كل دالة فيما يأتي بيانيًا، ثم حدد كلًا من مجالها ومداها: -3x x ≤ -4 ' f(x) = x, 0 < x ≤3 (12 x > 3 8, 2x, x≤-6 f(x) = 5, -6≤x≤2 (13 −2x + 1, x > 4 مثال 2 اكتب الدالة المتعددة التعريف الممثلة بيانيا في كلُّ ممَّا يأتي: (14 -2- 8642 -8- g(x) (16 g(x) فه -6- -8- (15 4 42 -4- -2- g(x) 88 -8- 6- -4- 2 2 4 6 8 x -8-6-4920 2 4 6 8 x -8-6-4-20 2 4 6 8 x -4- -4 -6 -4 -6 -8 |-8-6-4-20 مثال 3 17 جمعية خيرية تقوم جمعية خيرية بجمع الصدقات لإيصالها إلى مستحقيها، وتتبرع الجمعية أيضًا بمبلغ مساو لأي صدقة دون 100 ريال أو تساويها، كما تضيف الجمعية 100 ريال إلى أي صدقة تزيد على 100 ريال. حدّد نوع الدالة التي تمثل هذا الموقف. اكتب الدالة التي تصف هذا الموقف، ثم مثلها بيانيا. المثالان 34 مثل كل دالة فيما يأتي بيانيًا، ثم حدد كلًا من مجالها ومداها: h(x) = 3[x] −8 (19 h(x) = |2x|8 (22 h(x)=−3|0.5x+1|− 2 (25 f(x) = [x] - 6 (18) g(x)=x+2| (21 f(x) = 2|x − 4 | +6 (24 - (26 ترفيه يوضّح الجدول المجاور: تكلفة استئجار دباب شاطئ. جمعية البر الخيرية * a) حدد نوع الدالة التي تمثل هذا الموقف. (b) اكتب الدالة التي تمثل هذا الموقف، ثم مثلها بيانيًا. الربط مع الحياة f(x) = x - 5 | (20) k(x) = |−3x| +3 (23 استئجار الدبابات الشاطئية اكتب دالة القيمة المطلقة الممثلة بيانيًا في كل مما يأتي: تهدف جمعيات البر بالمملكة إلى ترسيخ مبدأ التكافل الاجتماعي بين أفراد المجتمع وتحويله إلى واقع عملي من خلال رعاية المحتاجين وتخفيف معاناتهم بتوفير الغذاء والدواء واللباس والأثاث. (27 f(x) 8642 -2- (28 f(x) 86 -8- -6- نه -8-6-4-20 2 4 6 8 x -8-6-4-20 246 8x -4 -4- -6 الزمن ) (ساعة) السعر (بالريال) 60 0<t≤ 12 2 1 100 <ts 1 2 160 240 1 <t≤ 2 2<t≤ 3 وزارة التعليم Ministry of Education الدرس 3-1 دوال خاصة 1 - 229

تهدف جمعيات البر بالمملكة إلى ترسيخ مبدأ التكافل الاجتماعي بين أفراد المجتمع وتحويله إلى واقع عملي من خلال رعاية المحتاجين
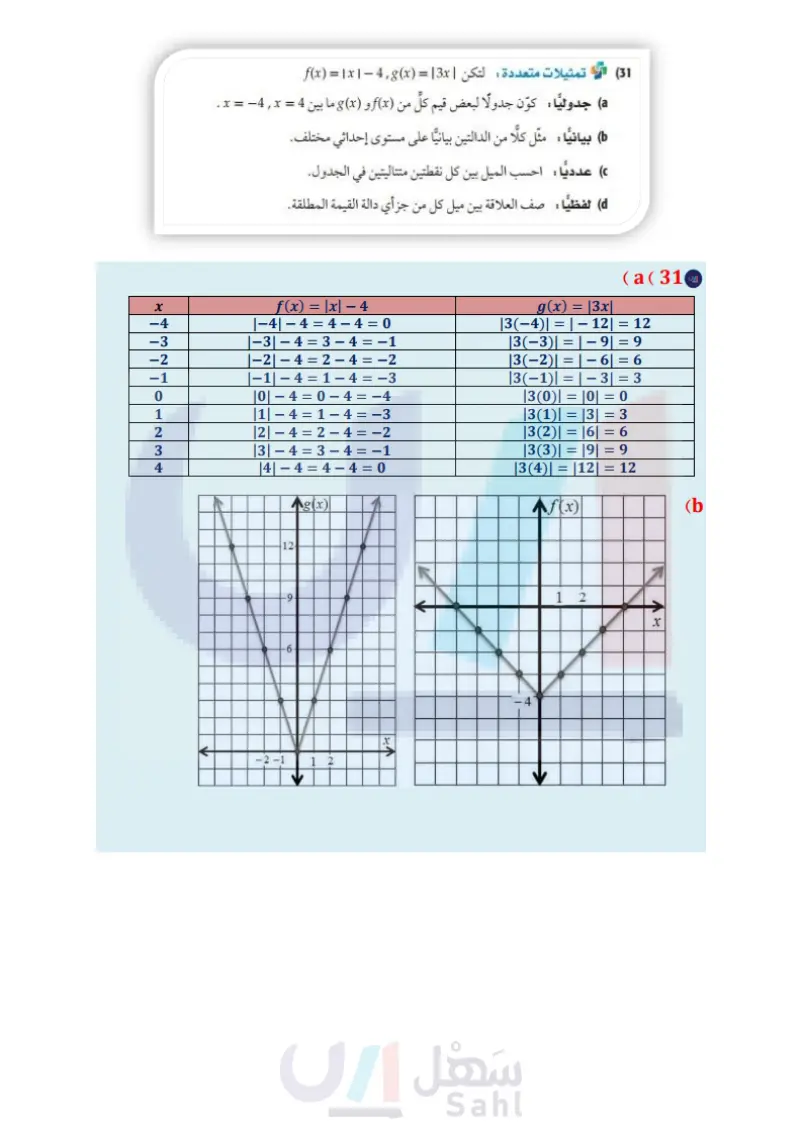
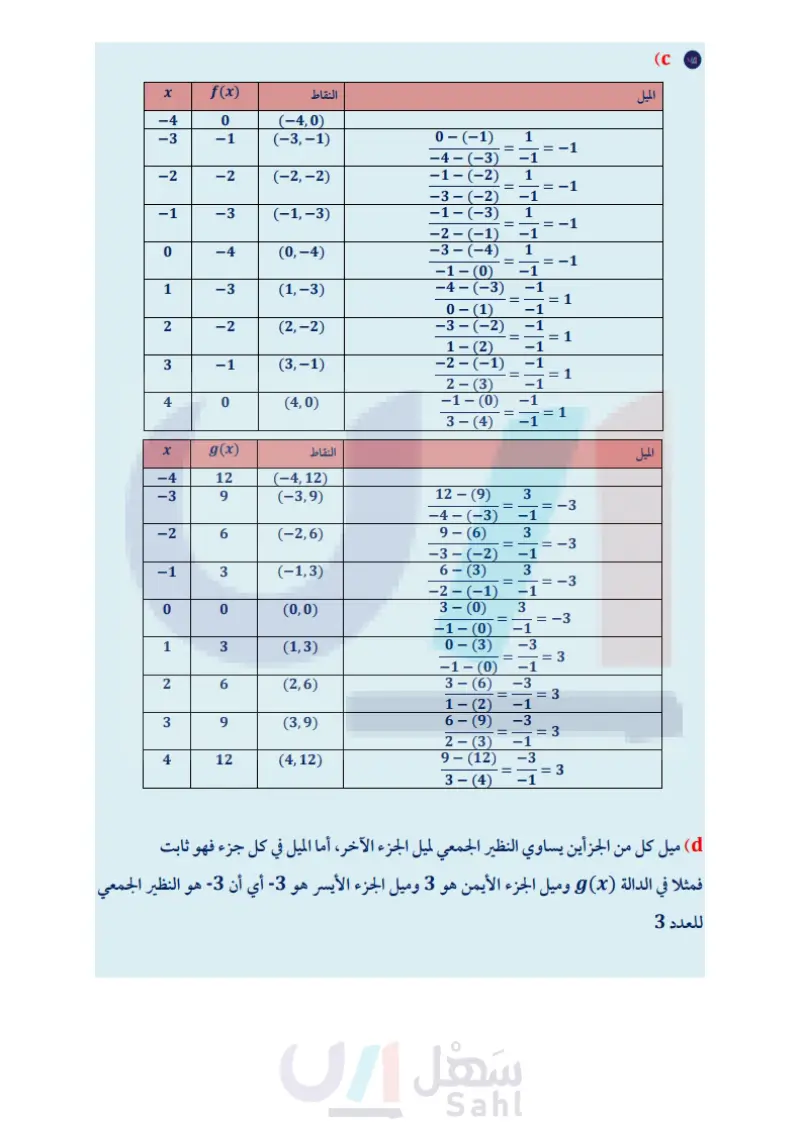
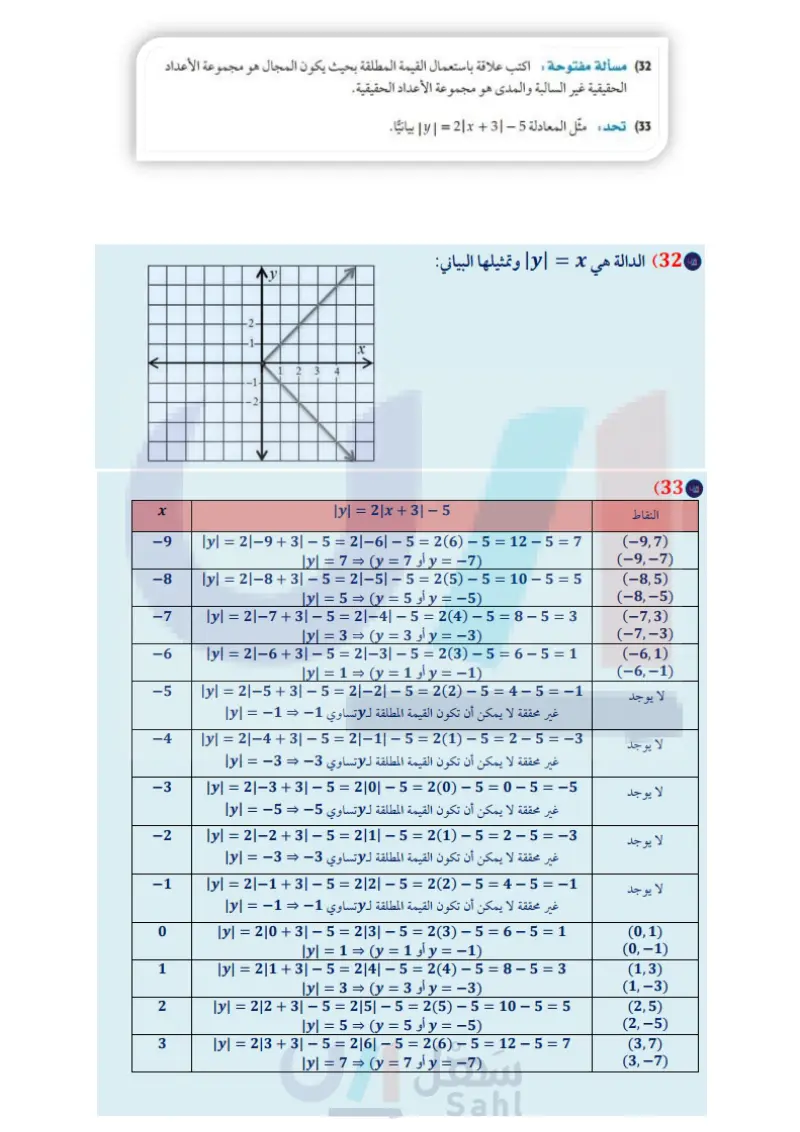
h(x)= مثْل كُل دالة فيما يأتي بيانيًا، ثم حدد كلًا من مجالها ومداها: -|x| x < −6 |x, 1-x, |−x\, -6≤ x ≤2 (30 x> 2 : [x], g(x) = x + 1, x+1, x < -4 −4≤x≤3 (29 -x, x > 3 (31) تمثيلات متعددة لتكن | f(x) = 1x | - 4,8(x) = 3x (a) جدوليًا : كوّن جدولاً لبعض قيم كلّ من (x) و (x) ما بين 4 = x = 4 x . (6) بيانيًّا : مثل كلا من الدالتين بيانيًّا على مستوى إحداثي مختلف. عدديًا : احسب الميل بين كل نقطتين متتاليتين في الجدول. d لفظيا صف العلاقة بين ميل كل من جزأي دالة القيمة المطلقة. : مسائل مهارات التفكير العليا ' - (32) مسألة مفتوحة : اكتب علاقة باستعمال القيمة المطلقة بحيث يكون المجال هو مجموعة الأعداد الحقيقية غير السالبة والمدى هو مجموعة الأعداد الحقيقية. (33) تحد: مثل المعادلة 5 - 3 + y | = 2 | x | بيانيًا. (34) تبرير : أعط مثالا مضادا للجملة الآتية، وفسّر إجابتك. "حتى تجد أكبر عدد صحيح لعدد غير صحيح x، فإنك تقرب x إلى أقرب عدد صحيح“ (35) مسألة مفتوحة : اكتب دالة قيمة مطلقة (f(x ، تحقق 3 - = (5)f (36) اكتب اشرح من خلال مثال كيف تستعمل الدوال المتعددة التعريف لتمثيل مسائل من واقع الحياة. وزارة التعليم Ministry of Education 2024-1446 تدريب على اختبار (37) إجابة قصيرة : ما العبارة التي تعطي الحد النوني للنمط (38) أي دالة مما يأتي يكون فيها 1- # ) ؟ f(x) = [x] C f(x) = [2x] D f(x) = 2x A f(x) = | 2x | B في الجدول التالي؟ 2 46 u | 8 ? 25 19 13 7 مراجعة تراكمية إذا كان 9 + f(x) = 4x + 6, (x) = -x2, h(x) = -2x2 – 6x، فأوجد كل قيمة مما يأتي: (الدرس (2-1) f(2c) (39 g(a + 1) (40 حدد مجموعات الأعداد التي ينتمي إليها كل عدد مما يأتي: (الدرس 1-1) h(6) (41 √11 (45 2|50 (44 -3 (43 الفصل 1 الدوال والمتباينات 36 (42) 30

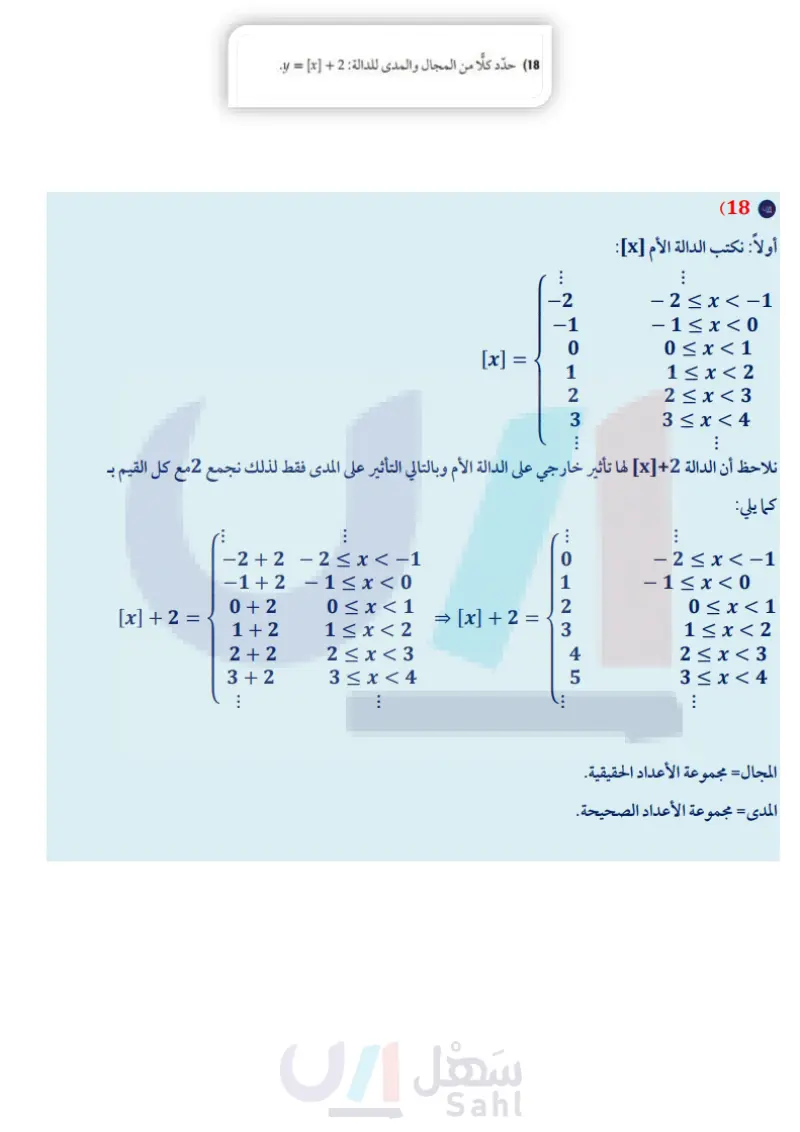
الفصل 1 اختبار منتصف الفصل الدروس -1-1 إلى 3-3-1 حدّد مجموعات الأعداد التي ينتمي إليها كل عدد مما يأتي: 25 (1 11 √50 (3 إذا كان 7 + f(x) = 3x3 – 2x، فأوجد قيمة كل مما يأتي : f(-2) (12 128 (2 32 f(2y) (13 -32.4 (4 f(1.4) (14 (5) اذكر الخاصية الموضحة في المعادلة الآتية: (4+15)7 = 4 (7) + 15 (7) (6) بسط العبارة -3(7a4b) + 2(-3a + b) (15) اختيار من متعدد : يقدر الدخل بالريال السيارة أجرة بالدالة 49 + f(x) = 0.35x، حيث x عدد الكيلومترات التي تقطعها السيارة. قدر دخل السيارة إذا قطعت km 250 . (7) ملابس يريد سعد شراء 3 قمصان و 3 بناطيل. فإذا كان سعر القميص الواحد 35 ريالًا . وسعر البنطال الواحد 55 ريالا. فأوجد المبلغ الذي يدفعه سعد بطريقتين مستعملا خاصية التوزيع. (8) اختيار من متعدد : أي العبارات التالية تكافئ § 1/3 (4m − 5n) + ½ ½ (2m + n) 46 m 15 - 47 -n A 15 46m 47n B ― A 84 ريالاً 112.50 ريالاً C 136.50 ريالاً D 215 ريالاً (16) مثل بيانيا الدالة: -x, f(x) = { x + 2, x<-2 -2 ≤ x 2 < 5, x>2 mn 15 C 5 m n D 8 (9) أوجد كلا من النظير الجمعي والنظير الضربي للعدد 2. 7 6 (10) حدد كلا من مجال العلاقة الآتية ومداها، ثم بين هل تمثل دالة أم لا: {(3, 2), (4, 1), (0, 3), (5,-2), (3,7)} :Y pi . (11) مثل المعادلة 3 - y = 2x بيانيا، ثم بين إذا كانت تمثل دالة أم لا. وهل هي متباينة أم لا؟ وهل هي منفصلة أم متصلة؟ (17) اكتب الدالة المتعددة التعريف الممثلة بيانيا فيما يأتي: 65432T -5 3 +2 1 1 2 3 4 5 x -5-4-3-20 --2- -3 -4- -5- که منطق 18) حدّد كلَّا من المجال والمدى للدالة : 2 + [y = [x. (19) مثل الدالة | f(x) = 12x ، ثم حدد كلًا من مجالها ومداها. وزارة التعليم Ministry of Education الفصل 1 اختبار منتصف الفصل 1 - 231




 0
0 
 0
0 

 0
0 

 0
0