إثبات تطابق المثلثات AAS ASA - رياضيات 1-2 - أول ثانوي
الفصل3: المثلثات المتطابقة
الفصل4: العلاقات في المثلث
الفصل5: الأشكال الرباعية
نشاط الفصل 3: المثلثات المتطابقة
نشاط الفصل 4: العلاقات في المثلث
نشاط الفصل 5: الأشكال الرباعية
www.jen.edu.sa إثبات تطابق المثلثات SAAS Proving Triangles Congruent-ASA, AAS 3-5 فيما سبق لماذا؟ درست إثبات تطابق مثلثين تتضمن مسابقات التجديف شخصين أو أكثر يجلسون ووجوههم نحو مؤخرة القارب، ولكل منهم مجداف. باستعمال SSSSAS (الدرس 4-3) والان أستعمل المسلمة ASA لاختبار التطابق أستعمل النظرية AAS لاختبار التطابق. المفردات: الضلع المحصور Included Side ويتطلب السباق عادة مسطحًا من الماء طوله 1500 متر على الأقل، ويمكن استعمال المثلثات المتطابقة لقياس المسافات التي يصعب قياسها مباشرة. مثل طول مضمار سباق الزوارق. مسلمة التطابق بزاويتين وضلع محصور بينهما :ASA الضلع الواقع بين زاويتين متتاليتين لمضلع يُسمى الضلع المحصور، ففي ABC المجاور ، AC هو الضلع المحصور بين AC C A أضف إلى مطويتك B B E D F مسلمة 3.3 التطابق بزاويتين وضلع محصور بينهما (ASA) إذا طابقت زاويتان والضلع المحصور بينهما في مثلث نظائرهما في مثلث آخر، فإن المثلثين متطابقان. مثال إذا كانت = A AB = DE , ZB = ZE, فإن ABC = DEF إنشاء هندسي إنشاء مثلث يطابق مثلثًا مرسومًا باستعمال مسلمة التطابق بزاويتين وضلع محصور بينهما (ASA) ارسم مثلثا وسمه AABC، ثم استعمل المسلّمة ASA لتنشئ AXYZ الذي يطابق AABC . B X Y A الخطوة 3: l X الخطوة 2 l أنشئ زاوية مطابقة لـ A عند النقطة X باستعمال XZ ضلعا للزاوية. أنشئ زاوية مطابقة لـ C عند النقطة 2 باستعمال XZ ضلعا للزاوية، وسمّ نقطة تقاطع الضلعين الجديدين للزاويتين Y. الدرس - إثبات تطابق المثلثات PSA PAAS 45 Ministry of Edu 2024-1446 الخطوة 1: ナ ارسم مستقيما ، واختر عليه النقطة X. وأنشئ XZ على أن تكون XZ = AC.

مثال 1 استعمال ASA لإثبات تطابق مثلثين اكتب برهانا ذا عمودين. المعطيات: QS تنصف LPQR .ZPSQZRSQ المطلوب: APQS = ARQS البرهان : العبارات (1) QS تنصف PSQ = RSQ ، PQR ZPQSZRQS (2 QSQS (3 APQSARQS (4 تحقق من فهمك (1) اكتب برهاناً حرا. المعطيات ZX تنصف WZY ، تنصف YXW المطلوب : AWXZ = AYXZ S Q المبررات 1) معطيات (2) تعريف منصف الزاوية (3) خاصية الانعكاس للتطابق ASA (4 W X Z P R إرشادات للدراسة SSA تطابق ضلعين وزاوية غير محصورة بينهما : بالرغم من أن تطابق ضلعين وزاوية غير محصورة بينهما لا يكفي لإثبات أن المثلثين متطابقان لكن تطابق زاويتين وضلع سواء أكان محصورًا بينهما أو غير محصور بينهما كاف لإثبات تطابق مثلثين نظرية التطابق بزاويتين وضلع غير محصور بينهما AAS تطابق زاويتين وضلع غير محصور يكفي لإثبات أن المثلثين متطابقان. وتُعدّ علاقة التطابق هذه نظرية؛ لأنه يمكن إثبات صحتها باستعمال نظرية الزاوية الثالثة. نظرية 3.5 التطابق بزاويتين وضلع غير محصور بينهما (AAS) أضف إلى مطويتك إذا طابقت زاويتان وضلع غير محصور بينهما في مثلث نظائرها في مثلث آخر يكون المثلثان متطابقين. مثال إذا كانت = A ZBZE, BC = EF, فإن AABC = ADEF برهان المعطيات: L = 0, M = R, MN = RS نظرية التطابق بزاويتين وضلع غير محصور بينهما (AAS) المطلوب : ALMN = AQRS البرهان : LLELQ معطى ZM ZR معطى ZNZS نظرية الزاوية الثالثة Q D C E S M R N B A 46 الفصل 3 المثلثات المتطابقة MN = RS معطى ALMN = AQRS ASA وزارة التعليم Ministry of Education 2024-1446

SSA تطابق ضلعين وزاوية غير محصورة بينهما
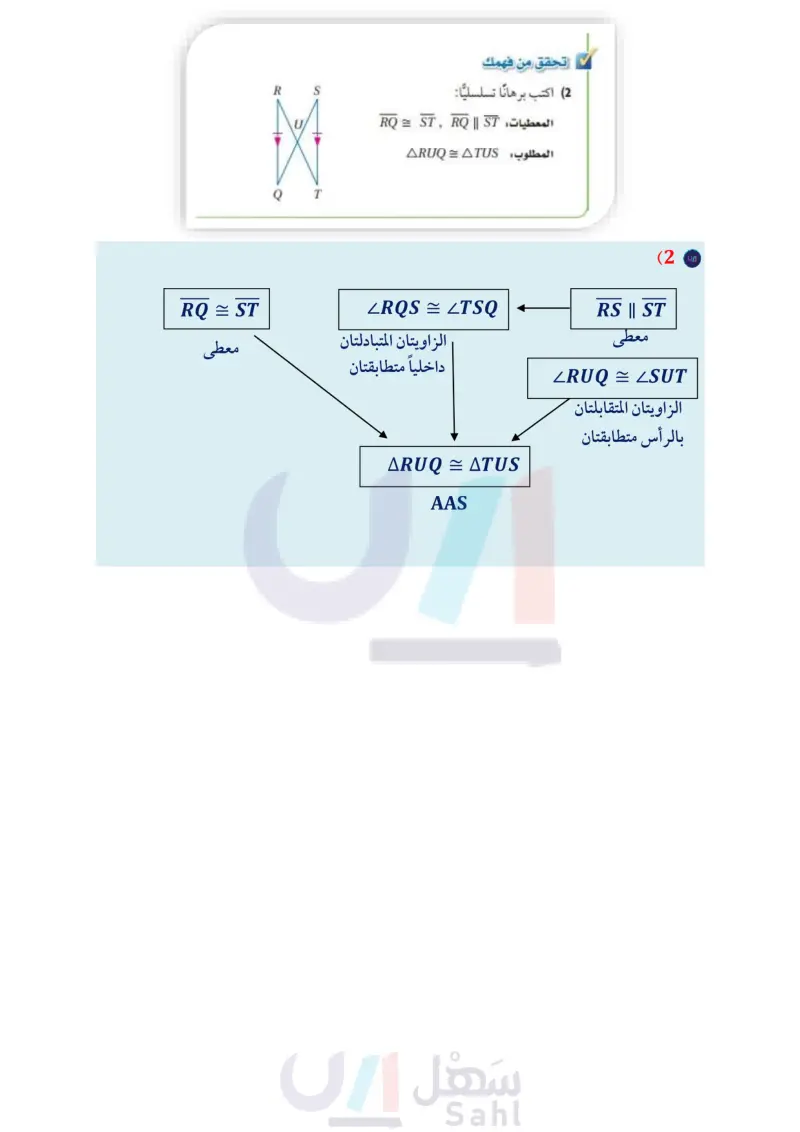
مثال 2 استعمال AAS لإثبات تطابق مثلثين اكتب برهانا حرا. المعطيات ,DAC = BEC DC= BC المطلوب : AACD = AECB البرهان بما أن DAC = BEC, DC = BC ، وأن C = بحسب خاصية الانعكاس، إذن AACD = ECB بحسب النظرية AAS. تحقق من فهمك (2) اكتب برهانا تسلسليا: المعطيات RQ = ST, RQ || ST المطلوب: ARUQ = ATUS R O T A B F E- D يمكنك استعمال المثلثات المتطابقة لقياس المسافات التي يصعب قياسها مباشرة. مثال 3 من واقع الحياة مسافات أراد أكرم أن يحسب المسافة بين النقطتين ، فقام بتعيين نقطة أخرى D ليستعملها نقطةً مرجعية، بحيث تكون العلاقات بين القطع المستقيمة كما في الشكل أدناه. إذا علمت أن طول DE يساوي ft 8، فاحسب المسافة بين النقطتين CB. إرشادات للدراسة زاوية - زاوية - زاوية B, E في المثال 3 متطابقتان بحسب نظرية الزاوية الثالثة إن تطابق الزوايا الثلاث المتناظرة غير لتحديد طول CB، يجب أولا أن نثبت أن المثلثين اللذين أنشأهما أكرم متطابقان. . بما أن CD عمودية على كلِّ من B ,DE كما هو مبين في الشكل، وجميع الزوايا القوائم متطابقة. . ZBCAZEDA 33 AC = AD • كاف لإثبات تطابق . BAC, LEAD زاويتان متقابلتان بالرأس إذن هما متطابقتان، وبحسب ASA ينتج أن BAC = AEAD وبما أن BAC E AEAD فإن DE = CB ؛ لأن العناصر المتناظرة متطابقة. وبما أن طول DE يساوي 8ft مثلثين. فإن طول CB يساوي 8ft أيضًا، وهي المسافة بين النقطتين CB. الدرس - إثبات تطابق المثلثات ASA AAS - 47 - Ministry of Educo 2024-1446

زاوية- زاوية- زاوية
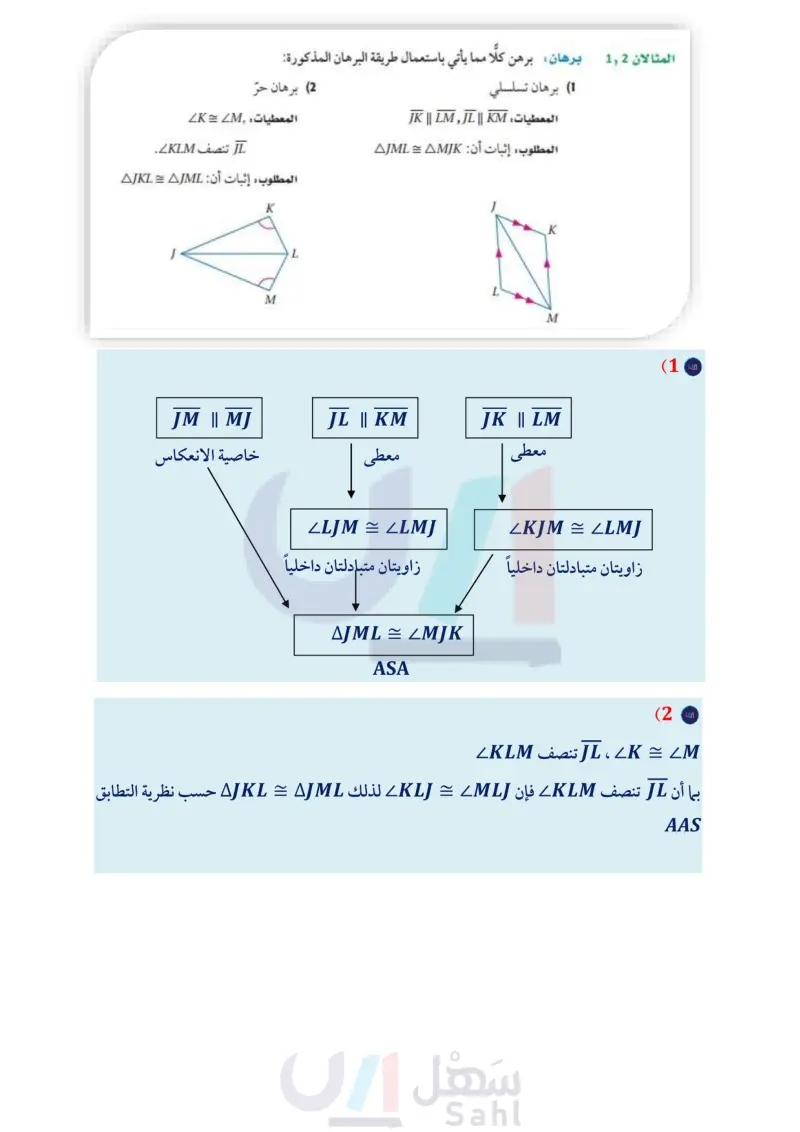
44 أضف إلى مطويتك وزارة التعليم Ministry of Education 2024-1446 C F E AAS تحقق من فهمك 3) استعمل الشكل المجاور الذي يمثل عمودي كهرباء وظليهما لكتابة برهان حرّ يبين أن BC = DE ASA تعلمت طرائق عديدة لإثبات تطابق المثلثات ملخص المفاهيم إثبات تطابق المثلثات SAS SSS يتطابق مثلثان إذا كانت يتطابق المثلثان إذا طابق يتطابق مثلثان إذا طابقت يتطابق مثلثان إذا طابقت زاويتان وضلع غير محصور بينهما في المثلث الأول نظائرها في المثلث الآخر. نظائرها في المثلث الآخر. نظائرها في المثلث الآخر. أضلاعُهما المتناظرة متطابقة. ضلعان والزاوية المحصورة زاويتان والضلع المحصور بينهما في المثلث الأول بينهما في المثلث الأول المثالان 1 برهان برهن كلًا مما يأتي باستعمال طريقة البرهان المذكورة: 1) برهان تسلسلي المعطيات JK || LM, JL || KM المطلوب إثبات أن: AJML = AMJK (2) برهان حر المعطيات KM تنصف KLM المطلوب : إثبات أن: AJKL = AJML K M L M المثال 3 (3) بناء جسور يحتاج مساح إلى إيجاد المسافة بين النقطتين . المبينتين في الشكل المجاور لبناء جسر فوق النهر. فوضع وتدا عند A، ووضع زميله وتدا عند B في الجهة المقابلة، ثم عين المساح النقطة C في نقطة جهة A ، بحيث كانت CA LAB . ووضع وتدا رابعًا عند E ، التي هي : منتصف CA . وأخيرًا وضع وتدا عند النقطة ،D ، بحيث كان CD I CA ، والنقاط D, E, B تقع على مستقيم واحد. a) وضح كيف يمكن أن يستعمل المسّاح المثلثين المتكونين لإيجاد المسافة بين النقطتين AB (6) إذا كان AC = 160m, DC = 60m, DE = 100m ، فأوجد المسافة بين النقطتين AB. ووضح إجابتك. تأكد الفصل 3 المثلثات المتطابقة 48

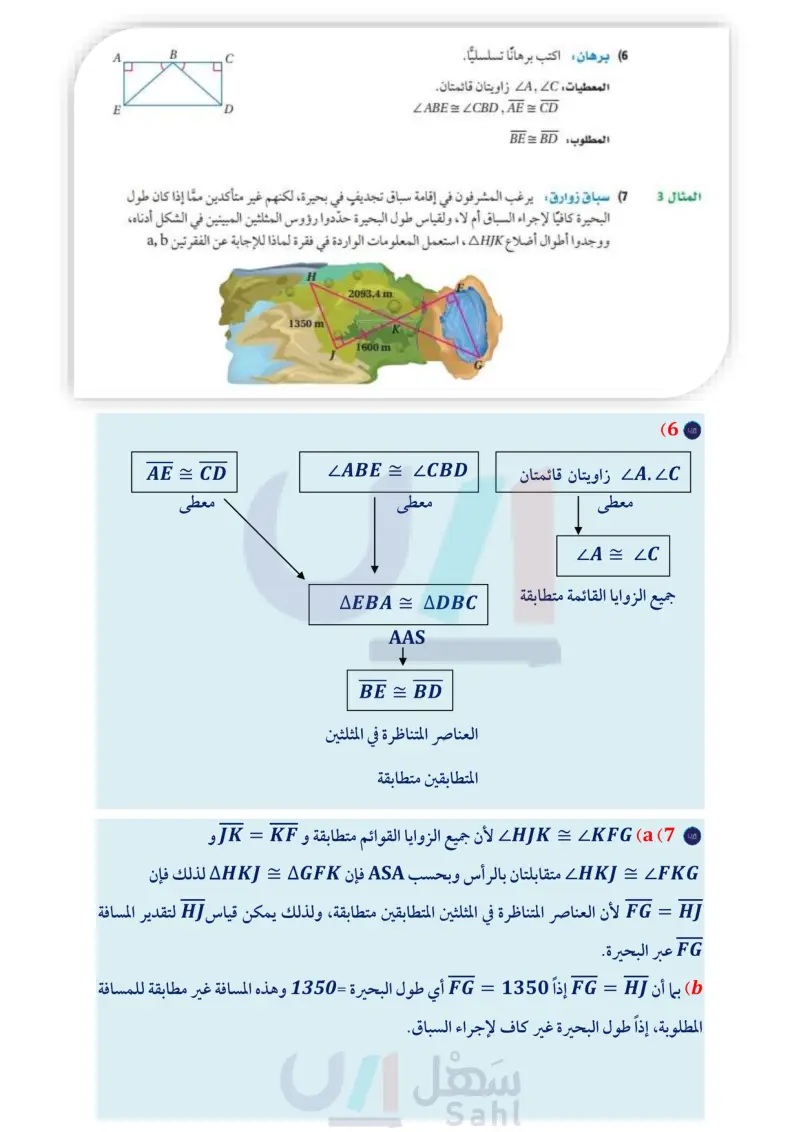
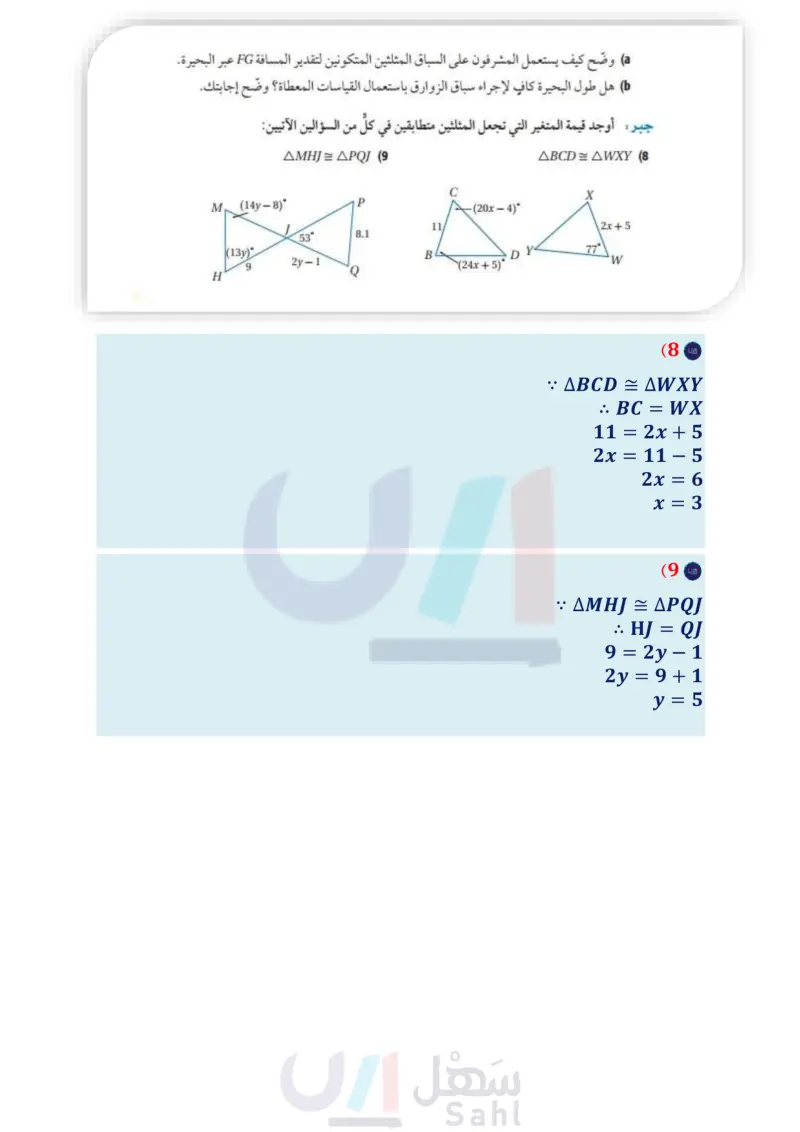
A W V A B C E D D B تدرب وحل المسائل المثال 1 برهان على الشكل المقابل (4) المعطيات AB || CD ZCBD ZBCA المطلوب : ACAB = ABDC المثال 2 برهان اكتب برهانا ذا عمودين. (5) المعطيات V نقطة منتصف WY XW || UY المطلوب AUVY = AXVW (6) برهان اكتب برهانا تسلسليا. المعطيات : A زاویتان قائمتان ZABE ZCBD, AE = CD المطلوب : BE = BD المثال 3 (7) سباق زوارق يرغب المشرفون في إقامة سباق تجديف في بحيرة، لكنهم غير متأكدين ممَّا إذا كان طول البحيرة كافيًا لإجراء السباق أم لا، ولقياس طول البحيرة حدّدوا رؤوس المثلثين المبينين في الشكل أدناه ووجدوا أطوال أضلاع AHJK ، استعمل المعلومات الواردة في فقرة لماذا للإجابة عن الفقرتين ab 2093.4 m 1350 m 1600 me a) وضح كيف يستعمل المشرفون على السباق المثلثين المتكونين لتقدير المسافة FG عبر البحيرة. ) هل طول البحيرة كافٍ لإجراء سباق الزوارق باستعمال القياسات المعطاة؟ وضح إجابتك. جبر أوجد قيمة المتغير التي تجعل المثلثين متطابقين في كلُّ من السؤالين الآتيين AMHJ = APQ (9 ABCDAWXY (8 X M (14y-8)° P (20x-4)° 11, 53° 8.1 2x+5 (13y) 2y-1 B D y 77° (24x+5)° W H الدرس - إثبات تطابق المثلثات PASA PAAS 49 Ministry of Ed 2024-1446

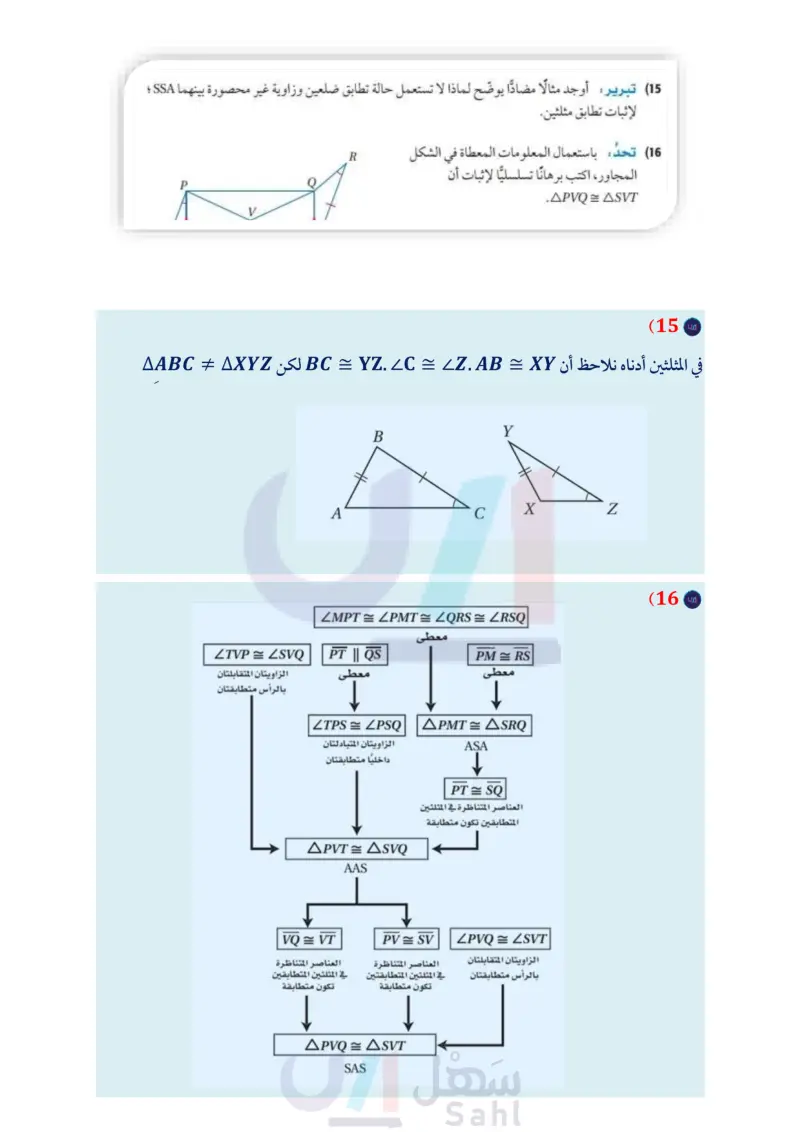
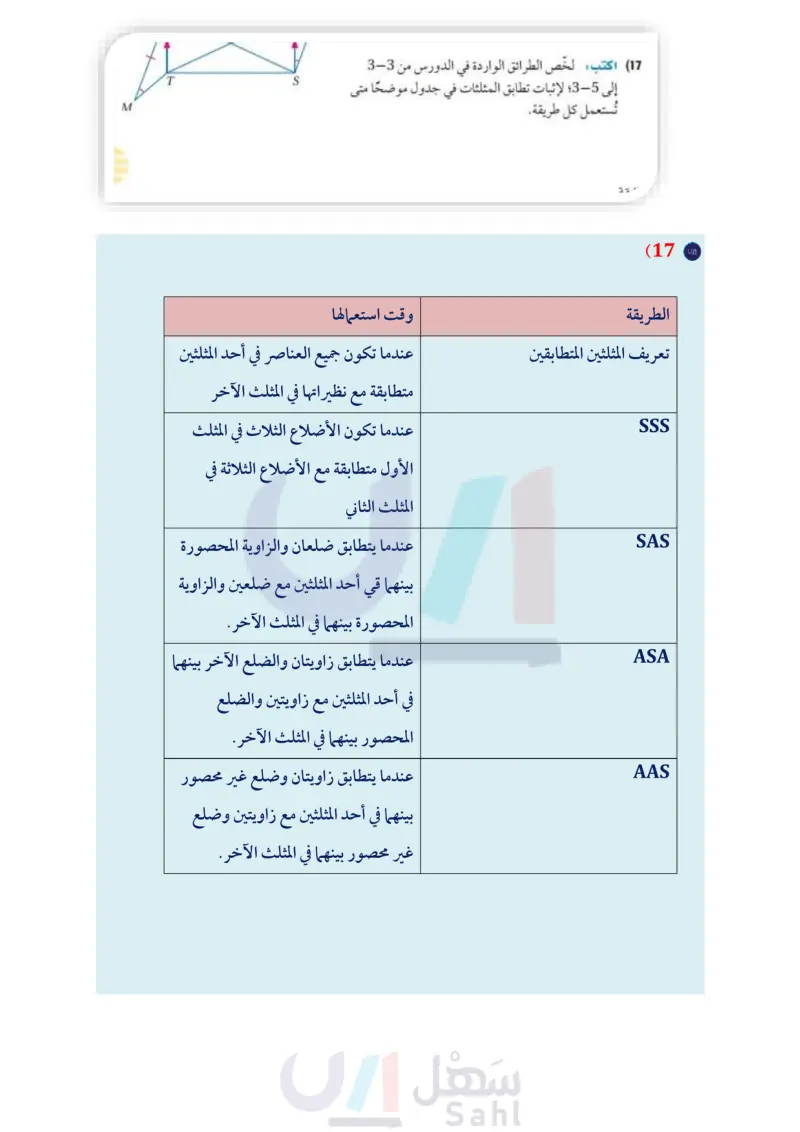
الربط مع الحياة برهان اكتب برهانا ذا عمودين (10) المعطيات , K = M, KP 1 PR MR 1 PR 11 المعطيات QR = SR = WR = VR المطلوب : QT= WU المطلوب : LKPL = LMRL M R T M S K R U W يعتمد حجم الدراجة الهوائية (12) دراجات هوائية: يشكّل أنبوب مقعد الدراجة مثلثًا مع كلّ من دعامتي السلسلة والمقعد. إذا كانت كل على طول أنبوب المقعد دعامة مقعد تشكل زاوية قياسها 68 مع دعامة السلسلة المناظرة لها، وكل دعامة سلسلة تشكل زاوية قياسها 44 مع أنبوب المقعد، فبيّن أن دعامتي المقعد لهما الطول نفسه. فيها. ويتراوح هذا الطول في الدراجات الهوائية للشباب ما بين 12in إلى 26in وتعتبر ملائمة للراكب إذا استطاع أن يركب الدراجة بسهولة وهو واقف على الأرض. أنبوب دعامتا المقعد دعامتا السلسلة C مسائل مهارات التفكير العليا (13) مسألة مفتوحة ارسم مثلثين يمكن إثبات تطابقهما باستعمال مسلمة ASA، وسمهما . (14) اكتشف الخطأ: يقول عمر إنه لا يمكن إثبات تطابق مثلثين بتطابق ثلاث زوايا AAA ، بينما يقول حسن إنه بإمكانه إثبات هذا التطابق، أيهما كانت إجابته صحيحة؟ وضح إجابتك. 15) تبرير أوجد مثالًا مضادا يوضح لماذا لا تستعمل حالة تطابق ضلعين وزاوية غير محصورة بينهما SSA ؛ لإثبات تطابق مثلثين. (16) تحد : باستعمال المعلومات المعطاة في الشكل المجاور، اكتب برهانا تسلسليا لإثبات أن .APVQ = ASVT (17) اكتب لخص الطرائق الواردة في الدورس من 3-3 إلى 35 لإثبات تطابق المثلثات في جدول موضحًا متى تُستعمل كل طريقة. R S V 50 الفصل 3 المثلثات المتطابقة وزارة التعليم Ministry of Education 2024-1446

أوجد مثالا مضادا يوضح لماذا لا تستعمل حالة تطابق ضلعين وزاوية غير محصورة بينهما SSA لإثبات تطابق مثلثين

يعتمد حجم الدراجة الهوائية على طول أنبوب المقعد فيها
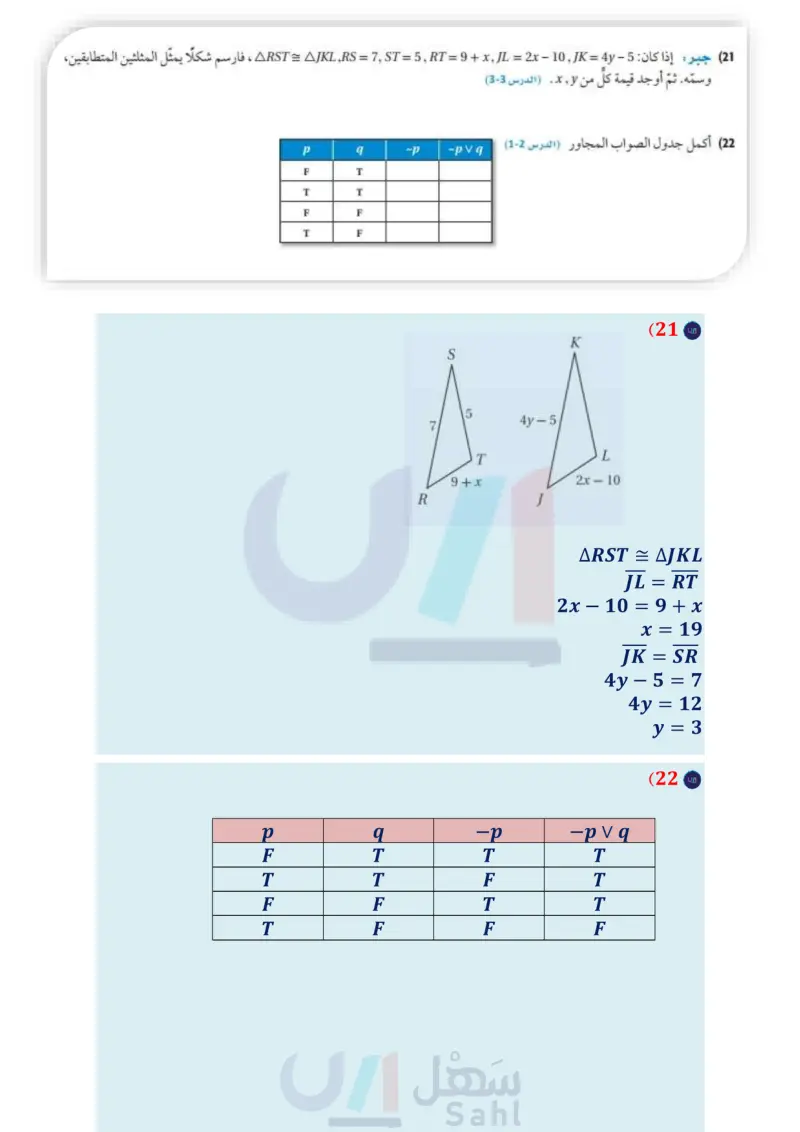
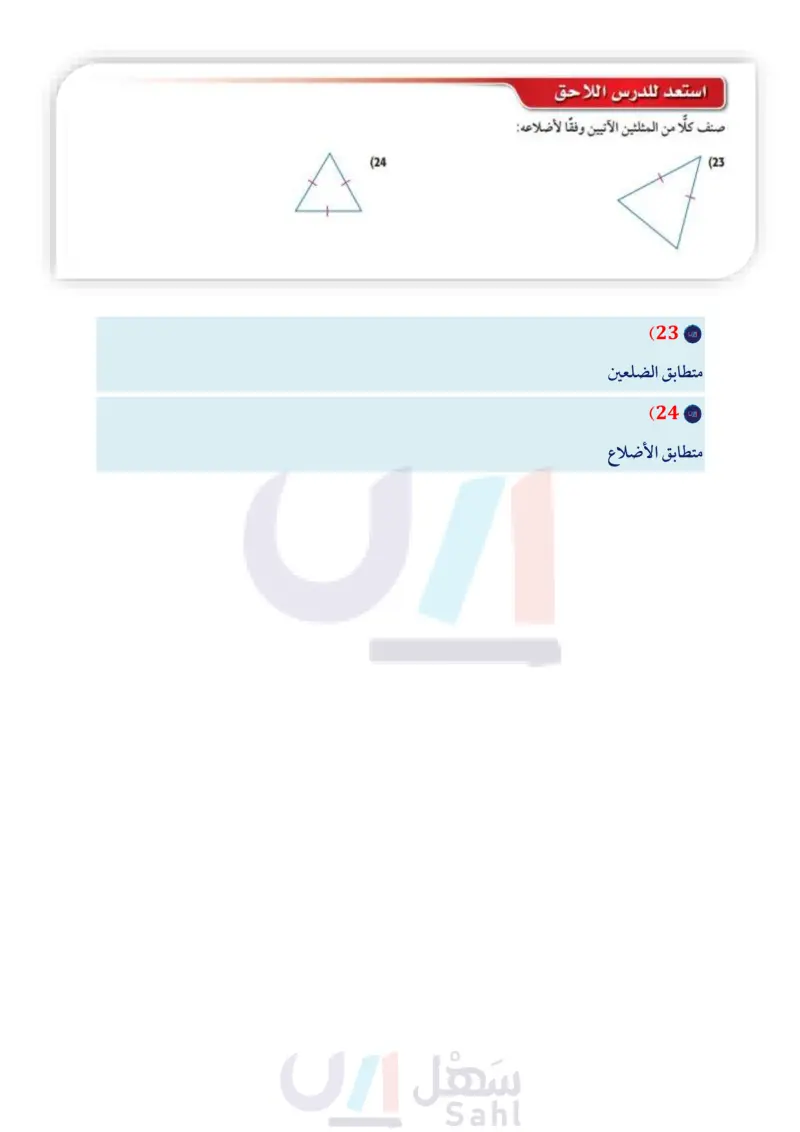
(19) ما قيمة 104 + 121 ؟ 15 (A 21 (B 125 (C 225 (D A تدريب على اختبار 18) في الشكل أدناه BCLAD, 2122 .D أي نظرية أو مسلّمة مما يأتي يمكن استعمالها لإثبات أن SAS (C SSS (D {AABC = ADBC AAS (A ASA (B مراجعة تراكمية 20 إذا علمت أن (031)B1, 6), C( - 9, 5, X ,(6) ، فبين ما إذا كان AABC = AXYZ أم لا . ووضح إجابتك (الدرس 4-3) (21) جبر إذا كان : 5 - ARST = RAJKL ,RS = 7, ST = 5, RT = 9 + x, JL = 2x - 110, JK = 4y ، فارسم شكلا يمثل المثلثين المتطابقين، وسمه. ثم أوجد قيمة كل من لا, . (الدرس (3-3) (22) أكمل جدول الصواب المجاور (مهارة سابقة) الدرس - إثبات تطابق المثلثات SAG AS 51 inistry of Edu 2024-1446 P q -p -pvq F T T T F F T F A (24 استعد للدرس اللاحق صنف كلا من المثلثين الآتيين وفقا لأضلاعه: (23




 1
1