المثلثات المتطابقة الضلعين والمثلثات المتطابقة الأضلاع - رياضيات 1-2 - أول ثانوي
الفصل3: المثلثات المتطابقة
الفصل4: العلاقات في المثلث
الفصل5: الأشكال الرباعية
نشاط الفصل 3: المثلثات المتطابقة
نشاط الفصل 4: العلاقات في المثلث
نشاط الفصل 5: الأشكال الرباعية
الساق 12 أضف إلى مطويتك D وزارة التعليم Ministry of Education 2024-1446 D F المثلثات المتطابقة الضلعين والمثلثات المتطابقة الأضلاع القاعدة A C الساق 3 Isosceles and Equilateral Triangles B E 3-6 فيما سبق: درست المثلثات المتطابقة الضلعين والمثلثات المتطابقة الأضلاع الدرس (1-3) وانان . أستعمل خصائص المثلثات المتطابقة الضلعين. أستعمل خصائص المثلثات المتطابقة الأضلاع المفردات: ساقا المثلث المتطابق الضلعين legs of an isosceles triangle لماذا؟ للعبة القطار السريع في مدينة الألعاب دعائم مثلثية بين المسارات لتقويتها وتثبيتها، والدعائم المثلثية الظاهرة في الصورة عبارة عن مثلثات متطابقة الضلعين خصائص المثلث المتطابق الضلعين تذكر أن المثلثات المتطابقة الضلعين لها ضلعان متطابقان على الأقل، وأن لعناصرها أسماء خاصة. حيث يُسمّى الضلعان المتطابقان الساقين، والزاوية التي ضلعاها الساقان تُسمّى زاوية الرأس. ويُسمى ضلع المثلث المقابل لزاوية الرأس القاعدة. والزاويتان المكونتان من القاعدة والضلعين المتطابقين تسميان زاويتي القاعدة. ففي الشكل المجاور، 1 هي زاوية الرأس، وزاويتا القاعدة هما 23. نظريات المثلث المتطابق الضلعين 3.10 نظرية المثلث المتطابق الضلعين إذا تطابق ضلعان في مثلث، فإن الزاويتين المقابلتين لهما متطابقتان. مثال : إذا كان AC = BC ، فإن 2 = 1 . 11. عكس نظرية المثلث المتطابق الضلعين إذا تطابقت زاويتان في مثلث، فإن الضلعين المقابلين لهما متطابقان. مثال: إذا كان 2 = 1 ، فإن FE = DE ستبرهن النظرية 3.11 في السؤال 24 مثال 1 القطع المستقيمة المتطابقة والزوايا المتطابقة سم زاويتين متطابقتين غير المشار إلى تطابقهما في الشكل. ACB تقابل B ،AB تقابل AC ؛ لذا فإن ACB = B . سم قطعتين مستقيمتين متطابقتين غير المشار إلى تطابقهما في الشكل. AD تقابل AC ACD تقابل D ، لذا فإن AD = AC. B زاوية الرأس vertex angle زاويتا القاعدة base angles الفصل 3 المثلثات المتطابقة 54

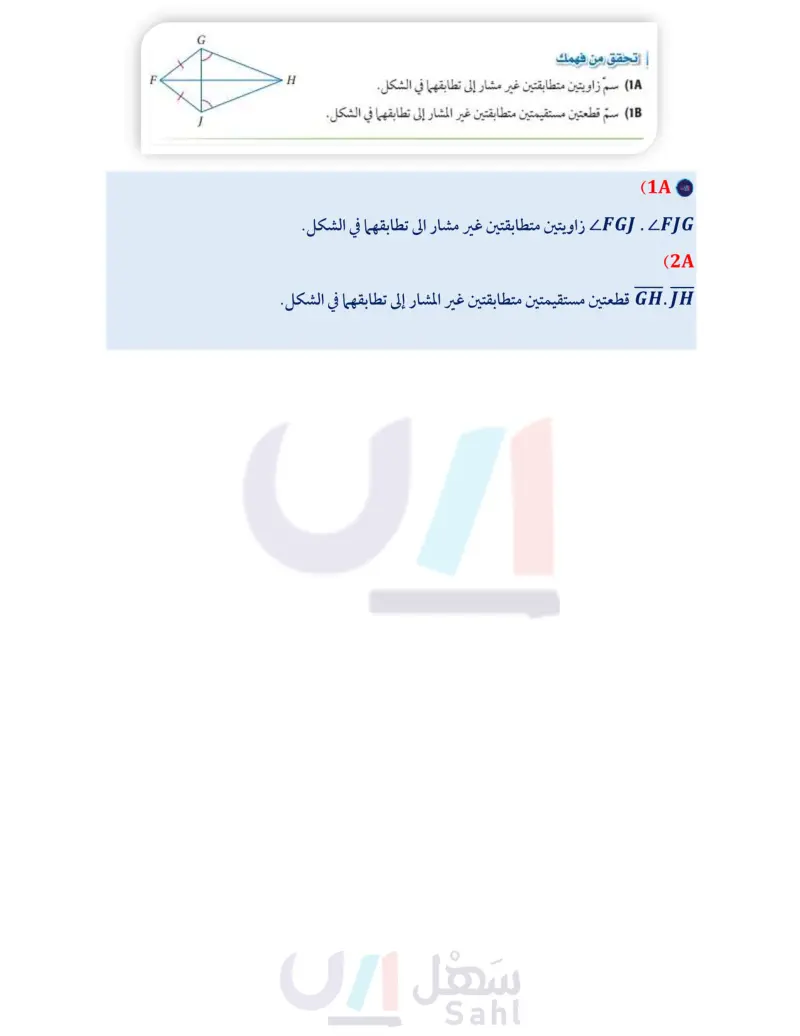
تحقق من فهمك 1 سم زاويتين متطابقتين غير مشار إلى تطابقهما في الشكل. 1B) سم قطعتين مستقيمتين متطابقتين غير المشار إلى تطابقهما في الشكل. H لإثبات نظرية المثلث المتطابق الضلعين، ارسم مستقيما مساعدًا، ثم استعمل المثلثين الناتجين. البرهان نظرية المثلث المتطابق الضلعين المعطيات في LM = IP ، ALMP المطلوب إثبات أن: MELP البرهان العبارات 1 افترض أن N نقطة منتصف MP . (2) ارسم قطعة مساعدة LN PN = NM (3 LNLN (4 LM = LP (5) ALMN=ALPN (6 ZMZP (7 M N P المبررات (1) كل قطعة مستقيمة لها نقطة منتصف واحدة. (2) كل نقطتين تحددان مستقيما. (3) نظرية نقطة المنتصف. (4) خاصية الانعكاس في التطابق. 5) معطى. (6) مسلّمة التطابق بثلاثة أضلاع (7) العناصر المتناظرة في مثلثين متطابقين تكون متطابقة. خصائص المثلث المتطابق الأضلاع نظرية المثلث المتطابق الضلعين تقود إلى نتيجتين حول زوايا المثلث المتطابق الأضلاع. مراجعة المفردات المثلث المتطابق الأضلاع : نتيجتان المثلث المتطابق الأضلاع هو مثلث أضلاعه الثلاثة متطابقة. 3.3 يكون المثلث متطابق الأضلاع إذا وفقط إذا كان متطابق الزوايا. مثال: A = B = C ، إذا وفقط إذا كان AB = BC = CA 3.4 قياس كل زاوية في المثلث المتطابق الأضلاع 60. مثال إذا كان DE = EF = FD ، فإن °60 = mLE = mLF = mLD. ستبرهن النتيجتين 3.3.4 في السؤالين 223 B C D 60° أضف إلى مطويتك 60° 60° F E الدرس - المثلثات المتطابقة الضلعين والمثلثات المتطابقة الأضلاع الت55 2024-1446

X 60 8 cm. A 8 cm. Y مثال 2 إيجاد القياسات المجهولة أوجد كل قياس من القياسات الآتية: mZY (a بما أن XY = X Y Z ، وباستعمال نظرية المثلث المتطابق الضلعين تكون زاويتا القاعدة متطابقتين؛ لذا فإن mZZ = mY. استعمل نظرية مجموع زوايا المثلث لإيجاد mY. Z نظرية مجموع زوايا المثلث mZX+ mZY+ mZZ = 180° mZX = 60°, mZZ = mLY 60° + mZY + mZY = 180° بسط اطرح 60 من كل طرف اقسم كل طرف على 2 60° + 2(mY) = 180° 2(mZY) = 120° mZY = 60° YZ (b mL = mY ؛ لذا بالتعويض فإن 60 = mLZ ، وبما أن 60 = mX ، فإن قياس كل زاوية من الزوايا الثلاث 60 ؛ لذا فالمثلث متطابق الزوايا. وهو متطابق الأضلاع أيضًا، لذا فإن XY = XZ = ZY. وبما أن XY = 8 cm ، إذن YZ = 8 cm M P 11cm 120° N وزارة التعليم Ministry of Education 2024-1446 3 in. (2x)° PN (2B تحقق من فهمك mZM (2A إرشادات للدراسة المثلثات المتطابقة الضلعين كما اكتشفت في المثال 2 ، أي مثلث متطابق الضلعين فيه زاوية قياسها 60 يكون مثلثا متطابق الأضلاع يمكنك استعمل خصائص المثلثات المتطابقة الأضلاع والجبر لتجد القيم المجهولة. مثال B إيجاد القيم المجهولة جبر أوجد قيمة كل متغير في الشكل المجاور. بما أن MA = MB؛ أي أن A = LB فإن AC = BC باستعمال عکس نظرية المثلث المتطابق الضلعين؛ وبذلك فإن أضلاع المثلث متطابقة. وقياس كل زاوية فيه تساوي 60 ؛ لذا فإن 30 = 2x = 60 x وبما أن المثلث متطابق الأضلاع، إذن جميع الأضلاع متطابقة. B (2x)" (4y-5) in. C 80° 4y-2 2y+2 (6x+8) AB = BC 3 = 4y - 5 8 = 4y 2 = y تعريف تطابق القطع المستقيمة عوض اجمع 5 إلى كل من الطرفين اقسم كل طرف على 4 تحقق من فهمك (3) أوجد قيمة كل من المتغيرين في الشكل المجاور . الفصل 3 المثلثات المتطابقة 56

مثال 4 من واقع الحياة تطبيق تطابق المثلثات بناء في الصورة المجاورة. AACE مثلث متطابق الأضلاع. F نقطة منتصف D AE نقطة منتصف B ،EC نقطة منتصف CA. . برهن أن AFBD متطابق الأضلاع. المعطيات AACE متطابق الأضلاع، و F نقطة منتصف AE، و D نقطة منتصف EC و B نقطة منتصف CA المطلوب : إثبات أن: AFBD متطابق الأضلاع. البرهان العبارات 1) ACE متطابق الأضلاع. المبررات (2) F نقطة منتصف AE ، و D نقطة منتصف EC و B نقطة منتصف CA. ور 1) معطى (2) معطى (3) المثلث المتطابق الأضلاع متطابق الزوايا (4) تعريف نقطة المنتصف (5) تعريف المثلث المتطابق الأضلاع (6) تعريف التطابق (7) خاصية الضرب (8) بالتعويض 9) تعريف التطابق 10) مسلّمة SAS (11) العناصر المتناظرة متطابقة. (12) تعريف المثلث المتطابق الأضلاع ZAZCZE (3 AF = FE, ED = DC, CB = BA (4) CA AE EC (5 CA = AE = EC 6 CA = 1 AB = 1 EC AE (1 2 (8 AF = FE = ED = DC = AB = BC AF = ED = CB, FE = DC = BA (9 AAFB = AEDF = ACBD 10 DF = FB = BD 11 12) AFBD متطابق الأضلاع تحقق من فهمك 4 في الصورة أعلاه إذا علمت أن AACE متطابق الأضلاع، فيه : BD || EF F || BC ، و D نقطة منتصف EC، فأثبت أن AFED = ABDC. B E R الربط مع الحياة استعمل المهندس المعماري في هذا المبنى قضبانا حديدية تم تثبيتها على شكل مثلثات لتزيد المبنى دعمًا وقوة مراعيا في ذلك الجوانب الجمالية للبناء أيضا. المثال 1 باستعمال الشكل المجاور أجب عن السؤالين الآتيين: (1) إذا كان AB = CB ، فسم زاويتين متطابقتين. (2) إذا كان LEAGUE ECA ، فسم قطعتين مستقيمتين متطابقتين. المثال 2 أوجد كلا من القياسين الآتيين: mZMRP (4 M الدرس - المثلثات المتطابقة الضلعين والمثلثات المتطابقة الأضلاع الت 57 Ministry of Ed 2024-1446 FH (3 F 60° /60° G H 12

استعمل المهندس المعماري في هذا المبنى قضبانا حديدة ثم تثبيتها على شكل مثلثات لتزيد المبنى دعما وقوة مراعيا في ذلك الجوانب الجمالية للبناء ايضا
A S 8 X 62° W 8 (4x-2)° R Y (6 المثال 3 جبر أوجد قيمة المتغير في كل من السؤالين الآتيين: (5 R 2z-15 9 S 7 T المثال 4 (7) القاطرة السريعة : الشكل المجاور يظهر جزءًا من سكة القاطرة السريعة المبينة في فقرة "لماذا؟" مكوّنة من مثلثات. إذا كان ST ، QR عمودیان علی ، QT و ARVS متطابق الضلعين قاعدته QT || R S ، فأثبت أن ARQV = ASTV. إذا كان QR = 2m ، VR = 2.5m ، فأوجد البعد بين المستقيمين ST و QR . برر إجابتك. C D B E وزارة التعليم Ministry of Education 2024-1446 F H H 60° تدرب وحل المسائل المثال 1 باستعمال الشكل المجاور أجب عن الأسئلة 11-8 : 8) إذا كان AB E ، فسم زاويتين متطابقتين. 9) إذا كانت ABFE LAFB ، فسم قطعتين مستقيمتين متطابقتين. (10) إذا كانت CADA ، فسم زاويتين متطابقتين. (11) إذا كانت DAE DEA فسم قطعتين مستقيمتين متطابقتين. المثال 2 أوجد كلًا من القياسين الآتيين: TR (13 P mBAC (12 A .B 60% 4 R E (15 .G (3x+6)° H M K L C المثال 3 جبر أوجد قيمة المتغير في كل من السؤالين الآتيين: 2x+11 (14 6.x-9 المثال 4 برهان اكتب برهانا حرا. (16) المعطيات AHJM متطابق الضلعين AHKL متطابق الأضلاع. المطلوب إثبات أن : JHK = CMHL الفصل 3 المثلثات المتطابقة 58

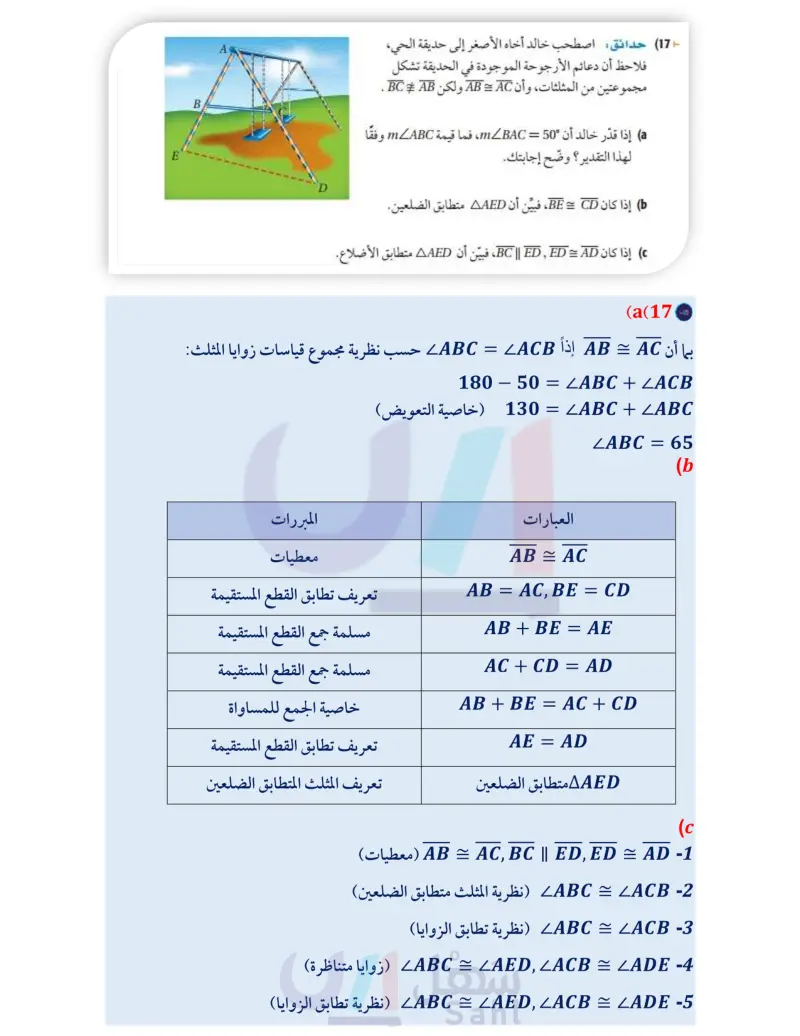
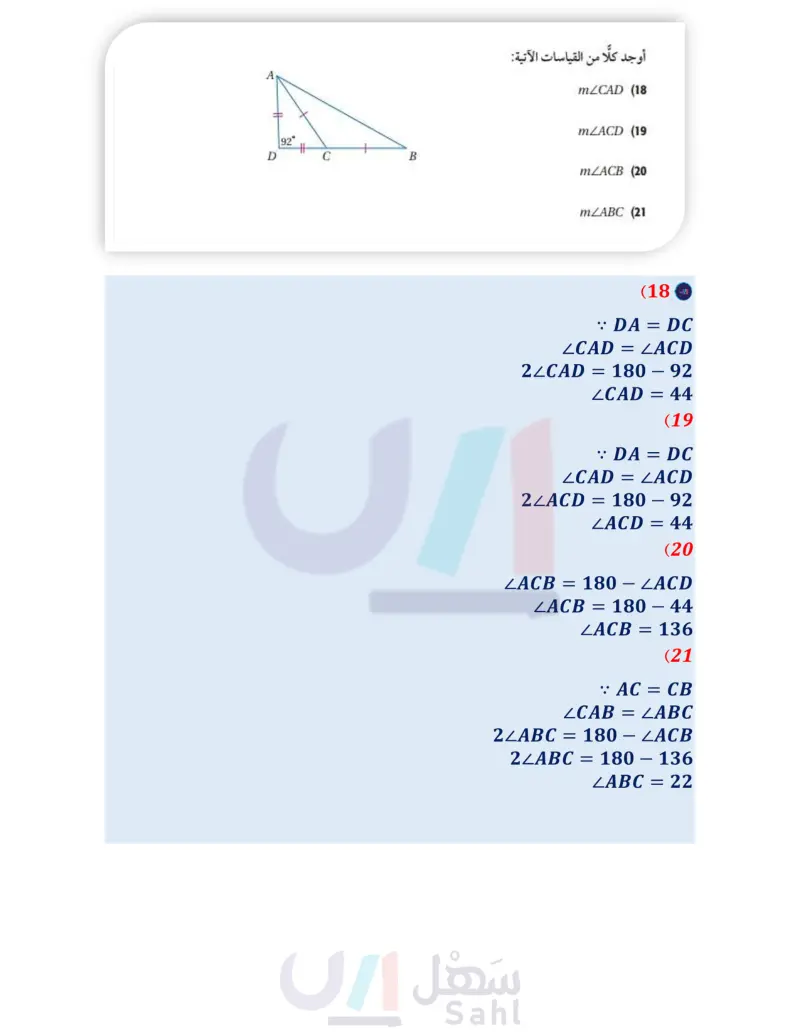
الربط مع الحياة مهمة الوالدين اختيار الألعاب التي تناسب أعمار أطفالهم. 17) حدائق اصطحب خالد أخاه الأصغر إلى حديقة الحي، فلاحظ أن دعائم الأرجوحة الموجودة في الحديقة تشكل مجموعتين من المثلثات، وأن AB = AC ولكن BC AB . إذا قدر خالد أن 50 = MBAC، فما قيمة mLABC وفقًا لهذا التقدير ؟ وضح إجابتك. ) إذا كان BE CD ، فبين أن AAED متطابق الضلعين. إذا كان BC | ED ED AD، فبين أن AAED متطابق الأضلاع. أوجد كلا من القياسات الآتية: الربط مع الحياة دقة ساعة الرمل الزجاجية تعتمد على ثبات معدل تدفق الرمل الذي يعتمد على نسبة قطر الثقب إلى قطر حبات الرمل المستعملة. mZCAD (18 mZACD (19 92° D C B mZACB (20 mZABC (21 برهان اكتب برهانا ذا عمودين لكل نتيجة أو نظرية مما يأتي: (22) النتيجة 3.3 (23) النتيجة 3.4 أوجد قيمة المتغير في كل من السؤالين الآتيين: (25 24 x2 + 5x (24) النظرية 3.11 (26 (y2-62) (2y-5)° الساعات الرملية استعمل الساعة الرملية المبينة في الشكل المجاور، وأوجد كلا من القياسات الآتية: mLPM (27 mZLMP (28 mZJLK (29 mZJKL (30 K (2x+10)° M P> (3x-55)° الدرس - المثلثات المتطابقة الضلعين والمثلثات المتطابقة الأضلاع الت59م stry of Ed 2024-1446

مهمة الوالدين اختيار الالعاب التي تناسب أعمار اطفالهم
دقة ساعة الرمل الزجاجية تعتمد على ثبات معدل تدفق الرمل الذي يعتمد على نسبة قطر الثقب إلى قطر حبات الرمل المستعملة
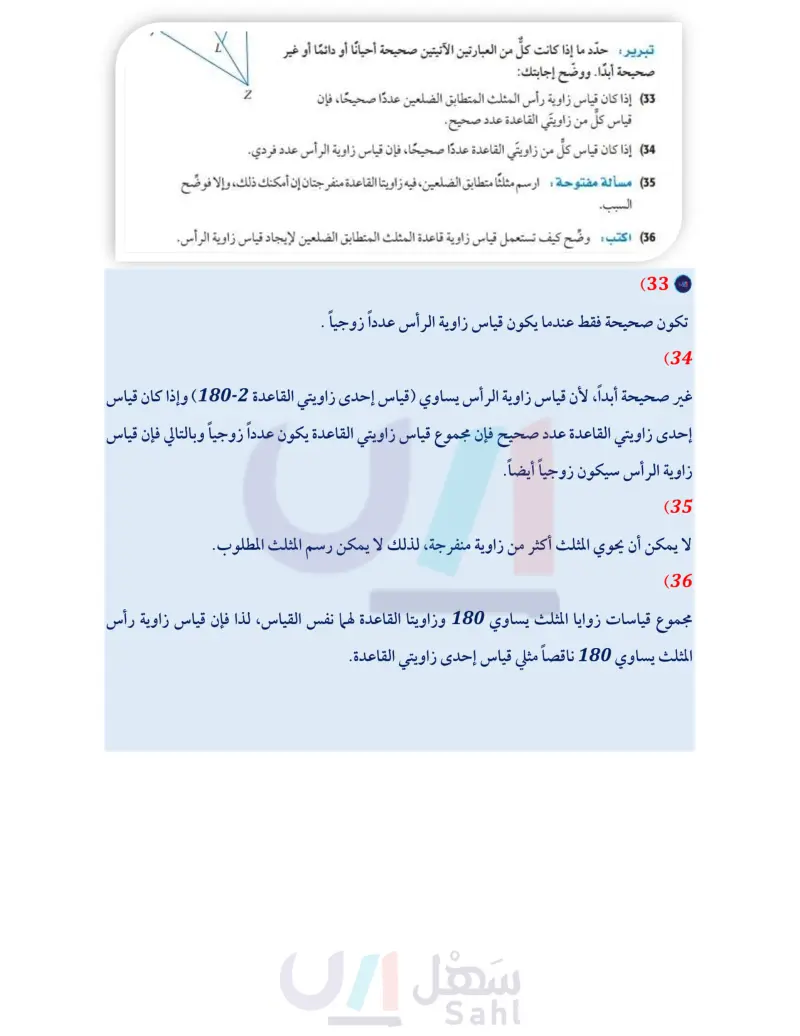
31) تمثيلات متعددة في هذه المسألة، ستكتشف القياسات الممكنة للزوايا الداخلية للمثلث المتطابق الضلعين، إذا علم قياس زاوية خارجية له. هندسيا : استعمل المسطرة والمنقلة لرسم ثلاثة مثلثات مختلفة، كلّ منها متطابق الضلعين. ومُدّ أحد ضلعي زاوية الرأس ومدّت القاعدة من إحدى جهتيها كما في الشكل المجاور. 1 B جدوليا : استعمل المنقلة لإيجاد m1 لكل مثلث وسجّله في جدول. واستعمل m21 لحساب قياسات 34 ، ثم أوجد 22 وسجله في جدول آخر واستعمله لحساب القياسات السابقة نفسها. رتّب نتائجك في جدولين. لفظيا : وضّح كيف استعملت 1 لإيجاد قياسات 34. ثم وضح كيف استعملت m22 لإيجاد هذه القياسات نفسها. جبريًا : إذا كان m1 = x ، فاكتب عبارة جبرية لإيجاد قياس كلّ من 345، وبالمثل إذا كان m2 = x ، فاكتب عبارة جبرية لإيجاد قياس كل من الزوايا نفسها. مسائل مهارات التفكير العليا 60 تدريب على اختبار 32) تحد في الشكل المجاور إذا كان AWIZ متطابق الأضلاع، ZWP = LWJM = LJZL ، فأثبت أن WP = ZL = JM. تبرير : حدد ما إذا كانت كل من العبارتين الآتيتين صحيحة أحيانًا أو دائمًا أو غير صحيحة أبدًا. ووضح إجابتك: (33) إذا كان قياس زاوية رأس المثلث المتطابق الضلعين عددًا صحيحًا، فإن قياس كل من زاويتي القاعدة عدد صحيح. (34) إذا كان قياس كل من زاويتي القاعدة عددًا صحيحًا، فإن قياس زاوية الرأس عدد فردي. W M P L (35) مسألة مفتوحة ارسم مثلثاً متطابق الضلعين، فيه زاويتا القاعدة منفرجتان إن أمكنك ذلك، وإلا فوضّح السبب. 36 اكتب وضح كيف تستعمل قياس زاوية قاعدة المثلث المتطابق الضلعين لإيجاد قياس زاوية الرأس. (37) في الشكل المجاور، AEBD تنصف كلُّ منهما الأخرى في النقطة C. أي المعلومات الإضافية الآتية تعد كافية لإثبات أن DE = DC؟ E 38) إذا كان 3 = x ، فإن قيمة 5 + 4x2 – 7x تساوي: 2 A B C D 20 B 42 C A 62 D ZACBZEDC C ZAZB D ZAZBCA A ZBZD B الفصل 3 المثلثات المتطابقة وزارة التعليم Ministry of Education 2024-1446

D B مراجعة تراكمية (39) إذا كان : CB = 7 in ، DC = 7 in AD = 27 in AB = 27 in فحدد ما إذا كان AADC = AABC. الدرس (34) اذكر الخاصية التي تبرر كلًا من العبارات الآتية: (مهارة سابقة) 40) إذا كان x y + ( = a ، فإن xy + xz = a (41) إذا كان 39 - 17 - n ، فإن 56 = n . (42) إذا كان 110 = mP + mQ وكانت 110 = MR ، فإن mZP + mZQ = mLR. (43) إذا كان 15 = CV = MD, MD فإن 15 = CV. B K A G C F H D E انظر إلى الشكل المجاور. (مهارة سابقة) (44) ما عدد المستويات الظاهرة في هذا الشكل؟ (45) سم ثلاث نقاط تقع على استقامة واحدة. استعد للدرس اللاحق أوجد إحداثيات نقطة المنتصف للقطعة التي إحداثيات طرفيها كما يأتي: الدرس - المثلثات المتطابقة الضلعين والمثلثات المتطابقة الأضلاع الت61 Ministry of Ed 2024-1446 A(2, 15), B(7, 9) (46 C(-4, 6), D(2,-12) (47 E(3, 2.5), F(7.5, 4) (48




 0
0 

 0
0 

 0
0