إثبات تطابق المثلثات SAS SSS - رياضيات 1-2 - أول ثانوي

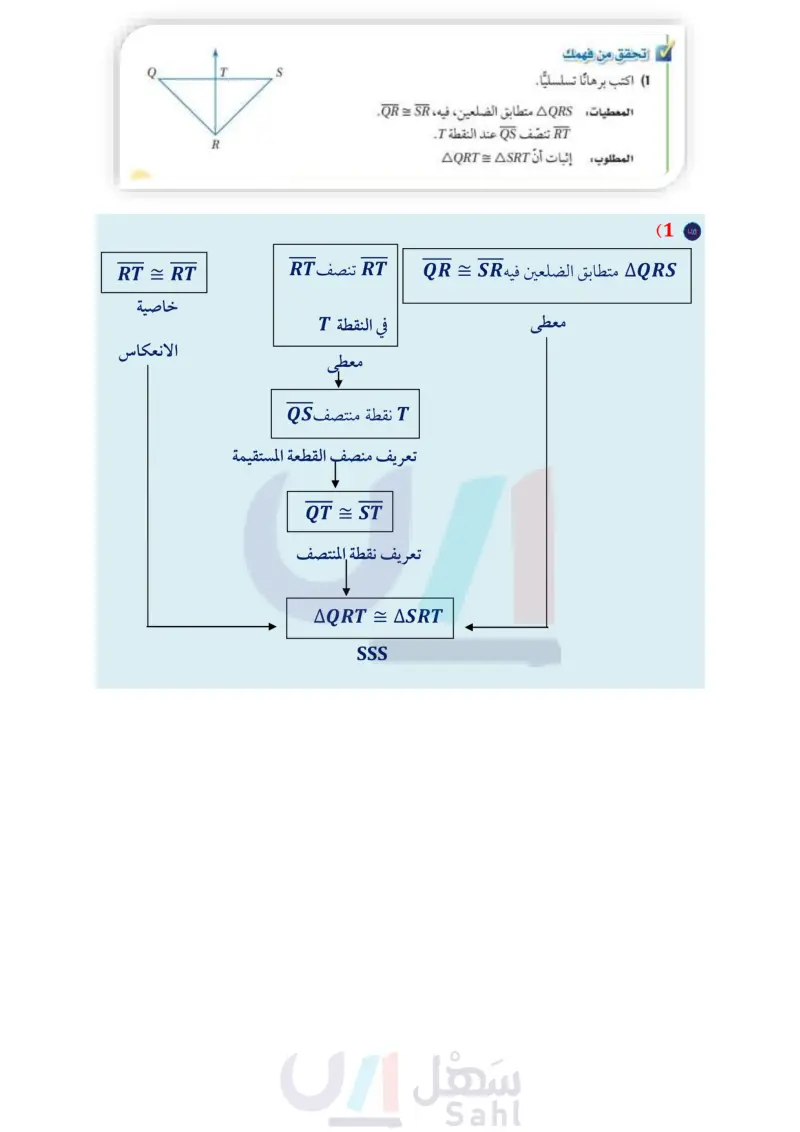
3-4 فيما سبق : إثبات تطابق المثلثات SSSSAS Proving Triangles Congruent-SSS, SAS الماذا؟ Z www.len.edu.sa لا تنس الواجب باستعمال تعريف التطابق درست إثبات تطابق المثلثات تُعدّ السبورة المزدوجة التي على شكل الحرف A طريقة مناسبة لعرض المعلومات، لا لأنها تُطوى عند التخزين فقط، ولكن لأنها تكون ثابتةً تماما عند . وضع الذراعين الجانبين في موقعيهما. وعندما يكون للذراعين الطول نفسه، ويتم تثبيتهما على أبعاد متساوية من القمة على الجانبين، فإن السبورة المفتوحة تشكل مثلثين متطابقين هما (الدرس (3-3) والان أستعمل المسلمة SSS .AABC,AXYZ لاختبار تطابق المثلثات مسلمة التطابق بثلاثة أضلاع SSS : في هذا الدرس ستكتشف أنه ليس من Y المنزلي الأحد القادم B أستعمل المسلمة SAS الضروري أن تبين تطابق الأضلاع المتناظرة وتطابق الزوايا المتناظرة في مثلثين لتثبت أنهما متطابقان. لاختبار تطابق المثلثات المفردات: الزاوية المحصورة Included Angle قراءة الرياضيات اختصارات رياضية اختصار لـ side تبين السبورة المزدوجة أنه إذا كانت أطوال الأضلاع المتناظرة لمثلثين متساوية، فإن المثلثين متطابقان. وهذا ما تنص عليه المسلمة الآتية: مسلمة 3.1 التطابق بثلاثة أضلاع (sss) إذا تطابقت أضلاع مثلث مع الأضلاع المناظرة لها في مثلث آخر، فإن المثلثين متطابقان. مثال إذا كان AB = DE , BC = EF, AC = DF ## F # D أضف إلى مطويتك B A فإن ABC = ADEF أو ضلع، و A اختصار ل Angle أو زاوية مثال 1 استعمال المسلمة SSS لإثبات تطابق مثلثين اكتب برهانا تسلسليا. المعطيات L GH = K, HL = JL نقطة منتصف GK. المطلوب إثبات أن AGHL = AKJL K البرهان . GH = K إرشادات للدراسة معطى منصف قطعة مستقيمة عبارة عن قطعة أو مستقيم أو مستوى يقطع HL JL معطى هي نقطة منتصف GK AGHL = AKJL SSS GLKL القطعة عند منتصفها. معطى تعريف نقطة المنتصف 36 الفصل 3 المثلثات المتطابقة تحقق من فهمك 1) اكتب برهانا تسلسليا. المعطيات AQRS متطابق الضلعين فيه، QR = SR. RT تنصف QS عند النقطة .T . المطلوب إثبات أن AQRT = ASRT F HI خ. G R A وزارة التعليم Ministry of Education 2024-1446

مثال 2 على اختبار معياري إجابة مطولة : إحداثيات رؤوس المثلث ABC هي : ((2) B(0, 3, C ,(1,1). .E(1, -1), F(2, -5), G(4, -4): ورؤوس المثلث EFG . هي : ( مثل كلا المثلثين في مستوى إحداثي واحد. استعمل هذا التمثيل؛ لتخمين ما إذا كان المثلثان متطابقين أم لا. وفسّر إجابتك. اكتب برهانًا منطقيا باستعمال الهندسة الإحداثية لتدعم تخمينك في الجزء b. اقرأ سؤال الاختبار: في هذه المسألة يُطلب إليك عمل ثلاثة أشياء؛ إذ يتعين عليك في الجزء a أن ترسم كلا من ABC, EFG في مستوى إحداثي واحد. وفي الجزء b أن تضع تخمينا يبين ما إذا كان AABC = AEFG أم لا، اعتمادًا على الرسم. وأخيرًا عليك في الجزء ، أن تثبت صحة تخمينك. حل سؤال الاختبار (a У C B يتضح من الرسم أن المثلثين مختلفان في الشكل؛ لذا يمكن أن نخمن أنهما ليسا متطابقين. A E استعمل صيغة المسافة لبيان أن أطوال بعض الأضلاع المتناظرة غير متساوية. AB = (0 - 12 + (3 - 1)2 V1 + 4 = V5 BC = √√(2-0)² + (5-3)² EF = √(2-1)²+[-5-(-1)]² = √1+16= √17 FG = √√(4-2)² + [−4 − (−5)]² V4 + 1 = V5 = V4 + 4 = V8 AC = (2 - 12 + (5 - 12 EG = = V1 + 16 = VI 1)² + [-4-(-1)]2 = V9 + 9 = V18 قراءة الرياضيات الرموز تقرأ العبارة وبما أن AB = FG, AC = EF، في حين أن BC EG ، فإن شروط مسلمة التطابق SSS غير متحققة؛ إذن .AABC = AEFG AABC = AEFG المثلث ABC لا يطابق المثلث EFG تحقق من فهمك (2) إحداثيات رؤوس المثلث هي (1),(25). ورؤوس المثلث NPQ هي .N(-3, 0), P(-7, 1), Q(-4, 4) مثل كلا المثلثين في مستوى إحداثي واحد. استعمل هذا التمثيل؛ لتخمين ما إذا كان المثلثان متطابقين أم لا. وفسر إجابتك. اكتب برهانا منطقيًا باستعمال الهندسة الإحداثية لتدعم تخمينك في الجزء B. الدرس 4- إثبات تطابق المثلثات SSSF SAS ال 37 Ministry of Edu 2024-1446

X A B Z إنشاء هندسي إنشاء مثلث يطابق مثلثا مرسومًا باستعمال المسلمة (SSS) ارسم مثلثا و اوسمه AABC ، ثم استعمل المسلمة SSS لتنشئ AXYZ الذي يطابق AABC . Z Z الخطوة 1 عين النقطة X على المستقيم .. ثم الخطوة 2 أنشئ قوسا طول نصف الخطوة 3 سم نقطة تقاطع القوسين وارسم XYZ لتشكل أنشئ XZ = AC على ) كما يأتي: . ركز رأس الفرجار في النقطة A ، وافتحه حتى يصل القلم إلى النقطة C. . باستعمال فتحة الفرجار نفسها، ركز رأس الفرجار في X، وارسم قوسا يقطع المستقيم ) وسم نقطة التقاطع Z. قطره AB، ومركزه X ، وقوسًا آخر طول نصف قطره BC، ومركزه Z (مستعملا الفرجار كما في الخطوة 1 ). .AXYZ مسلمة التطابق ضلعان والزاوية المحصورة بينهما SAS تُسمّى الزاوية المتكونة من ضلعين متجاورين لمضلع زاوية محصورة. تأمل الزاوية المحصورة والمتكونة من عقربي الساعة في كلا الوضعين الموضحين أدناه، ولاحظ أنه كلما شكل العقربان زاوية لها القياس نفسه، فستكون المسافتان بين طرفي العقربين IL, PR متساويتين. 12 APKR = AJKL 9 12 6 3 أي مثلثين يتكونان من زوجين من الأضلاع المتساوية في الطول وزاويتين محصورتين متساويتين في القياس يكونان متطابقين. وهذا يوضح المسلمة الآتية: مسلمة التطابق ضلعان والزاوية المحصورة بينهما (SAS) أضف الى طويتك وزارة التعليم Ministry of Education 2024-1446 B C E A F مسلمة 3.2 التعبير اللفظي إذا طابق ضلعان وزاوية محصورة بينهما في مثلث نظائرها في مثلث آخر، فإن المثلثين متطابقان مثال: إذا كان, AB = DE ZBZE, BC= EF, فإن AABC = ADEF. الفصل 3 المثلثات المتطابقة 38

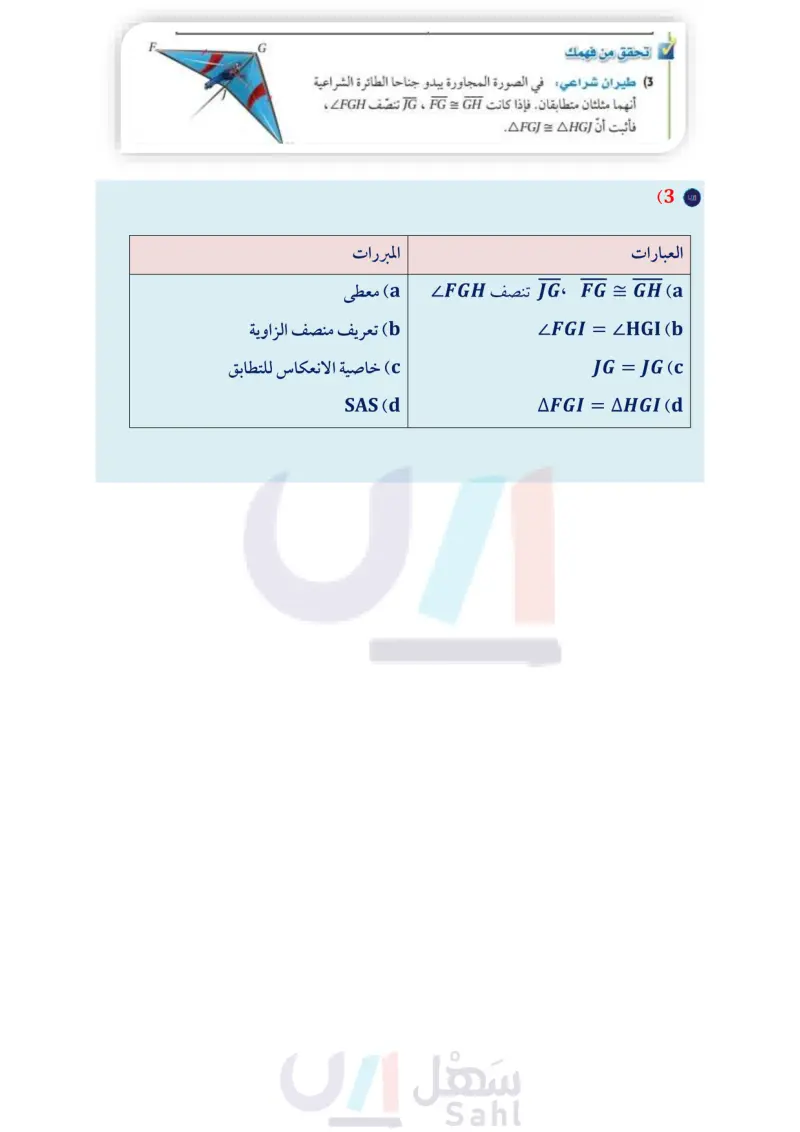
مثال 3 من واقع الحياة استعمال SAS لإثبات تطابق المثلثات إضاءة: تبدو دعامات السقالة حاملة المصابيح الظاهرة في الصورة وكأنها مكونة من مثلثات متطابقة. فإذا كان WX = ZY, WX | | ZY ، فاكتب برهانا ذا عمودين لإثبات أن: AWXZ = AYZX. البرهان : العبارات المبررات WX=ZY (1 1) معطى (2) معطى الربط مع الحياة فنيو الإضاءة: في صناعة الصور المتحركة، يقوم فنيو الإضاءة بتحديد مواقع المصابيح التي يتطلبها الفيلم. ويقوم هؤلاء الفنيون بالتأكد من أن الزوايا التي يشكلها الضوء في مواضعها الصحيحة. WX || ZY (2 ZWXZZXZY (3 XZ=ZX (4 AWXZ = AYZX (5 تحقق من فهمك (3) نظرية الزوايا الداخلية المتبادلة (4) خاصية الانعكاس للتطابق SAS (5 (3) طيران شراعي: في الصورة المجاورة يبدو جناحا الطائرة الشراعية أنهما مثلثان متطابقان. فإذا كانت TG ، G GH تنصف LFGH ، فأثبت أن AFGJ = AHG. Η G يمكنك أيضًا أن تنشئ مثلثات متطابقة إذا عُلم طولا ضلعين وقياس الزاوية المحصورة بينهما. إنشاء هندسي إنشاء مثلث يطابق مثلثا مرسومًا باستعمال مسلمة التطابق ضلعان والزاوية المحصورة بينهما (SAS) ' ارسم مثلئًا وسمه AABC ، ثم استعمل المسلمة SAS لتنشئ ARST الذي يطابق AABC . B " D A C E R N K m m R /N T R m T الخطوة 1 عين النقطة R على المستقيم الخطوة 2 أنشئ LR = LA ، باستعمال الخطوة 3 أنشئ RS = AB ، ثم ارسم ST لتشكل ARST. . ثم أنشئ RT = AC على m . RT ضلعا للزاوية، والنقطة R رأسًا لها كما يأتي: . ضع رأس الفرجار على النقطة A ، وارسم قوسا يقطع ضلعي A . سم نقطتي التقاطع . . باستعمال فتحة الفرجار نفسها، ضع رأس الفرجار عند R وارسم قوسا يبدأ فوق المستقيم " ويقطعه، سم نقطة التقاطع N .. ضع رأس الفرجار عند E وعدل الفتحة حتى يصل رأس القلم إلى D. . دون تغيير فتحة الفرجار، ضع رأس الفرجار عند النقطة ، وارسم قوسًا يقطع القوس الذي رسمته سابقا في النقطة K، ثم ارسم RK . الدرس 4- إثبات تطابق المثلثات SSSFSAS 39 2024-1446

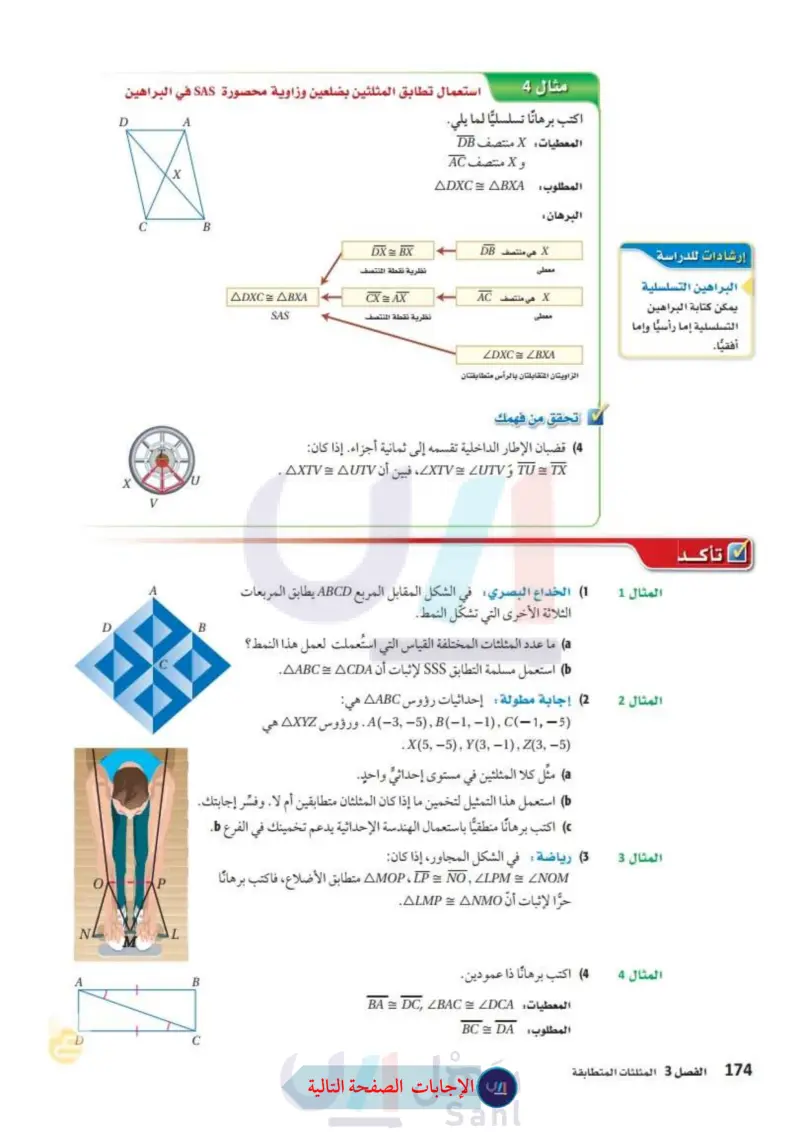
مثال 4 استعمال تطابق المثلثين بضلعين وزاوية محصورة SAS في البراهين اكتب برهانا تسلسليا لما يأتي. المعطيات X منتصف DB و X منتصف AC A D X C B X V B D O P NL A وزارة التعليم Ministry of Education 2024-1446 ADXC = ABXA SAS المطلوب : ADXC = ABXA البرهان : إرشادات للدراسة X هي منتصف DB DX= BX معطى نظرية نقطة المنتصف البراهين التسلسلية يمكن كتابة البراهين التسلسلية إما رأسيًا وإما X هي منتصف AC CX=AX معطى نظرية نقطة المنتصف أفقيا. ZDXC=ZBXA الزاويتان المتقابلتان بالرأس متطابقتان تحقق من فهمك (4) قضبان الإطار الداخلية تقسمه إلى ثمانية أجزاء. إذا كان TU = TX و XTV = UTV ، فبين أن AXTV = AUTV . المثال 1 1) الخداع البصري في الشكل المقابل المربع ABCD يطابق المربعات الثلاثة الأخرى التي تشكل النمط . ما عدد المثلثات المختلفة القياس التي استعملت لعمل هذا النمط ؟ b) استعمل مسلمة التطابق SSS لإثبات أن AABC = ACDA. المثال 2 (2) إجابة مطولة : إحداثيات رؤوس AABC هي: (5 ,1-)C ,(1,1) (35). ورؤوس AXYZ هي .X(5,-5), Y(3, -1), Z(3,-5) (a كلا المثلثين في مستوى إحداثي واحد. (6) استعمل هذا التمثيل لتخمين ما إذا كان المثلثان متطابقين أم لا. وفسر إجابتك. اكتب برهانا منطقياً باستعمال الهندسة الإحداثية يدعم تخمينك في الفرع .. المثال 3 (3) رياضة في الشكل المجاور، إذا كان MOP IP = IN CLPM = ZNOM متطابق الأضلاع، فاكتب برهانا حرا لإثبات أن ALMP = ANMO. B C المثال 4 (4) اكتب برهانا ذا عمودين. المعطيات BA = DC, BAC = DCA تأكد المطلوب : BC = DA الفصل 3 المثلثات المتطابقة 40

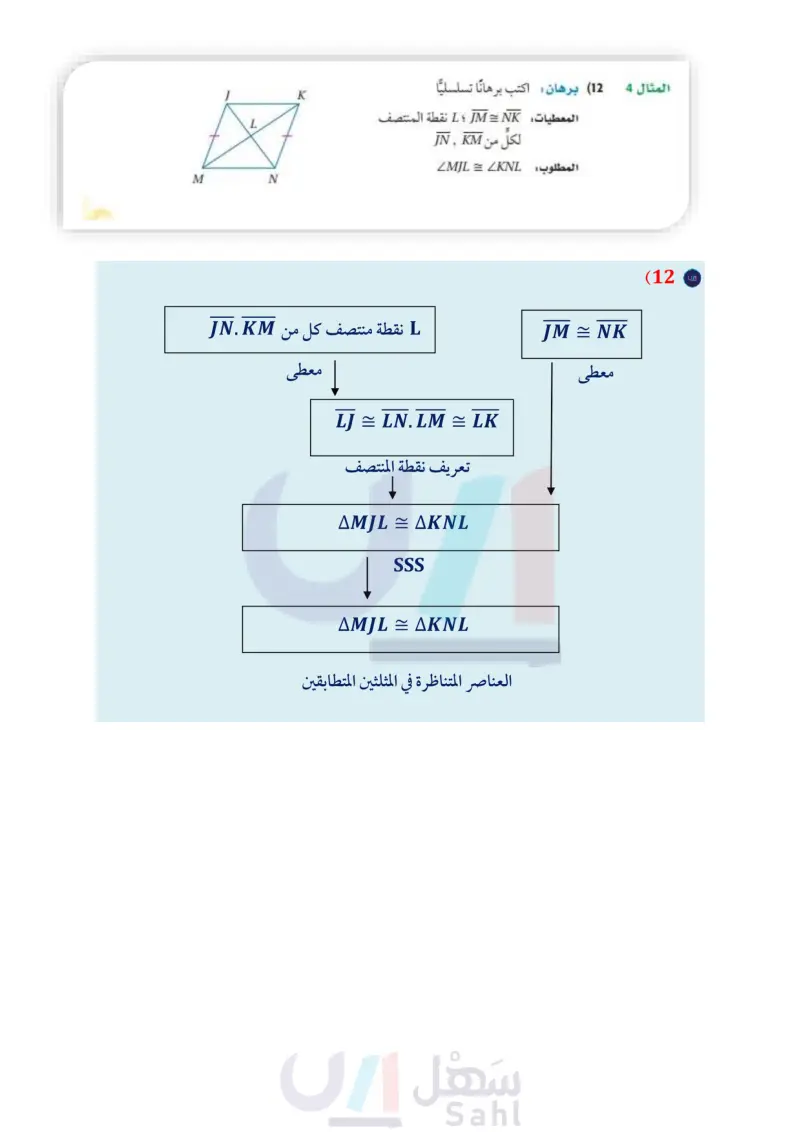
تدرب وحل المسائل المثال 1 برهان اكتب برهانا من النوع المذكور في كل من السؤالين الآتيين: (5) برهان حر المعطيات,QR = SR ST=QT المطلوب : AQRT = ASRT (6) برهان ذو عمودين المعطيات: AB = ED, CA = CE AC تنصف BD المطلوب : AABC = AEDC B A C D E 0 R T S (7) جسور جسر الرياض المعلق طوله m 763 ، وهو مثبت بحبال معدنية معلقة بدعامتين خرسانيتين. كما هو مبين بالشكل، بحيث يلتقي الحبلان المعدنيان العلويان في النقطة C عند منتصف المسافة بين الدعامتين، إذا كانت AB = ED: فأثبت أن المثلثين المبينين في الشكل المجاور متطابقان. B D المثال 2 حدد ما إذا كان AMNO = AQRS في كلُّ من السؤالين الآتيين، ووضح إجابتك: M(2, 5), N(5, 2), O(1, 1), Q(-4, 4), R(-7, 1), S(-3, 0) (8 M(0, -1), N(-1, -4), O(-4, -3), Q(3, -3), R(4, -4), S(3, 3) (9 المثال 3 برهان اكتب برهانًا من النوع المحدد في كل من السؤالين الآتيين: (10) برهان ذو عمودين المعطيات, BD 1 AC BD تنصف AC المطلوب : AABD = ACBD 11) برهان حر المعطيات: R نقطة المنتصف لكل من QS, PT المطلوب APRQ = ATRS Q P S R K L M N الدرس 4- إثبات تطابق المثلثات SSSF SAS الت41 Ministry of Edu 2024-1446 B A D C المثال 4 (12) برهان اكتب برهانا تسلسليا المعطيات: JM = NK ؛ نقطة المنتصف لكل من IN, KM المطلوب : LMJL = ZKNL

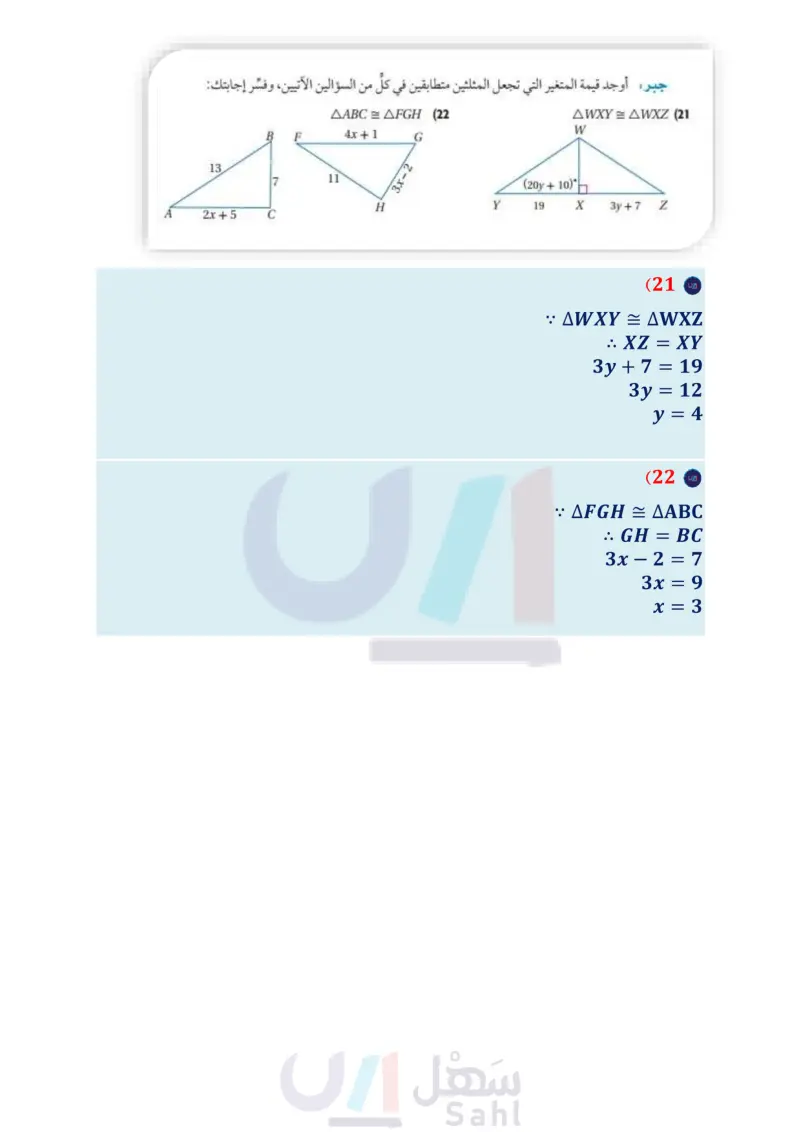
T D P احذر الانزلاق R B S 60 ft 60 ft C A 60 ft 60 ft X Y W Z G وزارة التعليم Ministry of Education 2024-1446 P M H حدد ما إذا كان المثلثان في كل من الأسئلة الآتية متطابقين أم لا. وضح إجابتك. (15 (14 (13 إرشادات للدراسة تطابق ضلعين وزاوية غير محصورة بينهما في مثلث مع نظائرها في مثلث آخر، لا يكفي لإثبات أن المثلثين متطابقان (16) إشارة تحذيرية: استعمل الشكل المجاور. a ما اسم المجسم الذي تمثله إشارة التحذير. إذا كان ABAD, CB = CD ، فأثبت أن AACB = AACD. لماذا يبدو المثلثان غير متطابقين في الشكل ؟ (17) برهان اكتب برهانا تسلسليا. المعطيات ATPQ = ASPR ZTQR = ZSRQ المطلوب: ATQR = ASRQ 18 في الشكل المجاور ABCD مزرعة مربعة الشكل، ويريد أخوان فصلها باستعمال سياج على أحد القطرين. a اكتب بره هانا ذا عمودين لإثبات أن BD = AC . اكتب برهانا ذا عمودين لإثبات أن BDC = BDA . L K إرشادات للدراسة الأشكال عند كتابة البراهين أو حل المسائل التي تتضمن مثلثات (19) برهان اكتب برهانا ذا عمودين. المعطيات YX = WZ, YX || ZW المطلوب : AYXZ = AWZX (20) برهان اكتب برهانا حرا. المعطيات HL = HM, PM = KL متطابقة، من المفيد أن ترسم شكلاً خاصا بك وتعين عليه الأضلاع والزوايا المتطابقة التي PG = KJ, GH =JH تجدها. المطلوب : LG = LJ جبر أوجد قيمة المتغير التي تجعل المثلثين متطابقين في كلّ من السؤالين الآتيين، وفسر إجابتك: AABC = AFGH (22 B F 4x + 1 G 13 7 11 H 2x+5 C 3x- 2 AWXY AWXZ (21 W (20y+10) Y 19 X 3y+7 Z الفصل 3 المثلثات المتطابقة 42 42

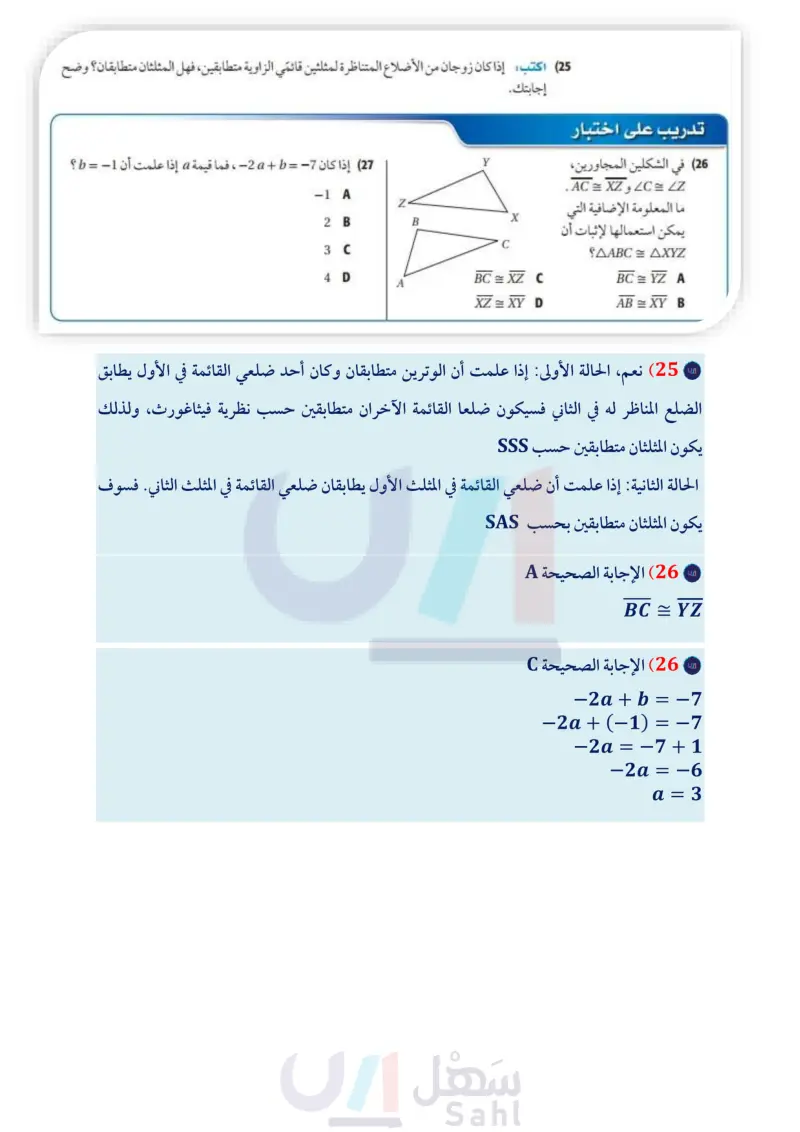
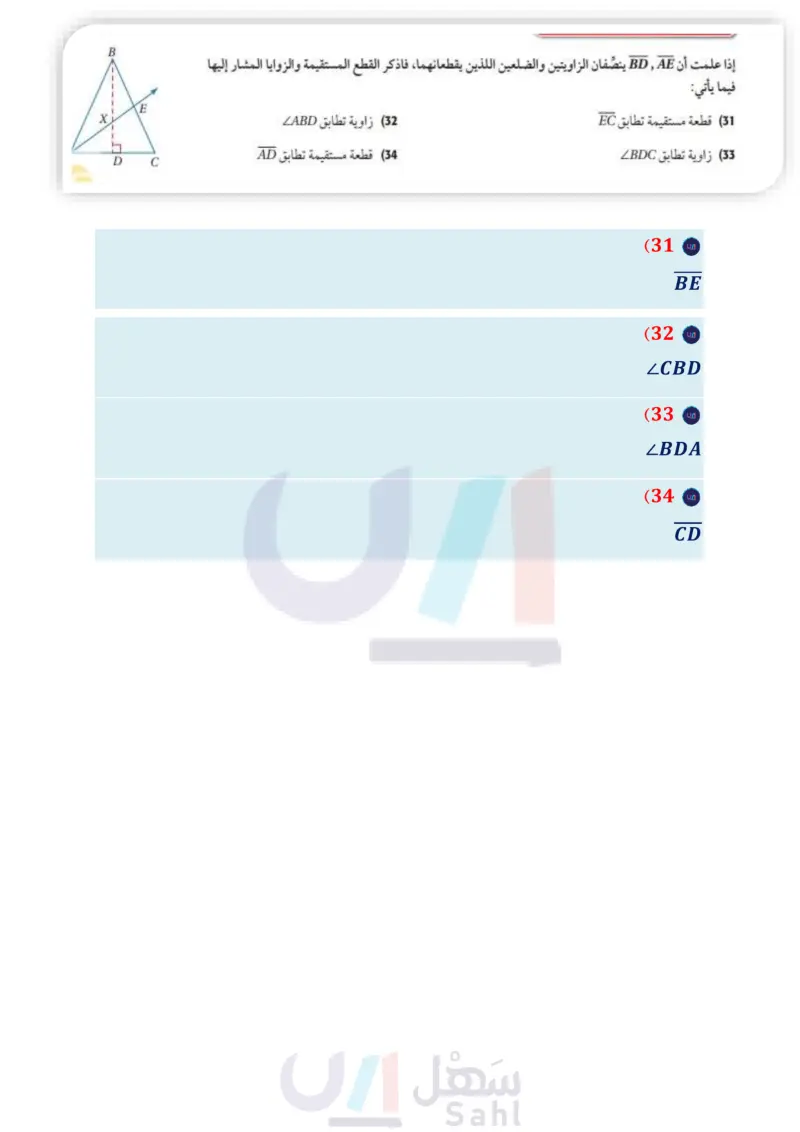
مسائل مهارات التفكير العليا تدريب على اختبار (23) تحد في الشكل المجاور: a صف طريقتين يمكنك استعمالهما لإثبات أنّ AWYZ يطابق AWYX. علما بأنه لا يُسمح باستعمال المسطرة أو المنقلة. وأي طريقة تعتقد أنها فعالة أكثر؟ وضح إجابتك. أثبت أن AWYZ = AWYX ووضح إجابتك. (24) اكتشف الخطأ قال :أحمد: إنّ APRQ = AXYZ بحسب SAS. فاعترض خالد :وقال لا توجد معلومات كافية لإثبات أن المثلثين متطابقان. أيهما كانت إجابته صحيحة؟ وضح إجابتك. R 0 X Z 59° Y 59° P 25 اكتب إذا كان زوجان من الأضلاع المتناظرة لمثلثين قائمي الزاوية متطابقين، فهل المثلثان متطابقان؟ وضح 26) في الشكلين المجاورين C = Z و AC = XZ. ما المعلومة الإضافية التي يمكن استعمالها لإثبات أن إجابتك. X (27) إذا كان 7 = b + 2 ، فما قيمة a إذا علمت أن 1- = b ؟ -1 A 2 B B C 3 C 4 D BC= XZ C !AABC = AXYZ BC=YZ A A XZ = XY D AB =XY B مراجعة تراكمية في الشكلين المجاورين، إذا علمت أن متوازي الأضلاع LMNP = متوازي الأضلاع QRST ، فأوجد: (الدرس (3-3) (28) قيمة X . (29) قيمة لا . T SN P 2x+10, \3x+5 (2y-12) Q R (y+6) M L (30) اكتب العكس والمعكوس والمعاكس الإيجابي للعبارة: "الزاويتان المتجاورتان على مستقيم متكاملتان . وحدد ما إذا كانت كل عبارة صحيحة أو خاطئة. وإذا كانت خاطئة، فأعط مثالا مضادا. (مهارة سابقة) استعد للدرس اللاحق إذا علمت أن BD AE ينصفان الزاويتين والضلعين اللذين يقطعانهما، فاذكر القطع المستقيمة والزوايا المشار إليها فيما يأتي: 31) قطعة مستقيمة تطابق EC (33) زاوية تطابق BDC (32) زاوية تطابق ABD (34) قطعة مستقيمة تطابق AD B X A D C الدرس 4- إثبات تطابق المثلثات SSSF SAS 43 Ministry of Ed 2024-1446

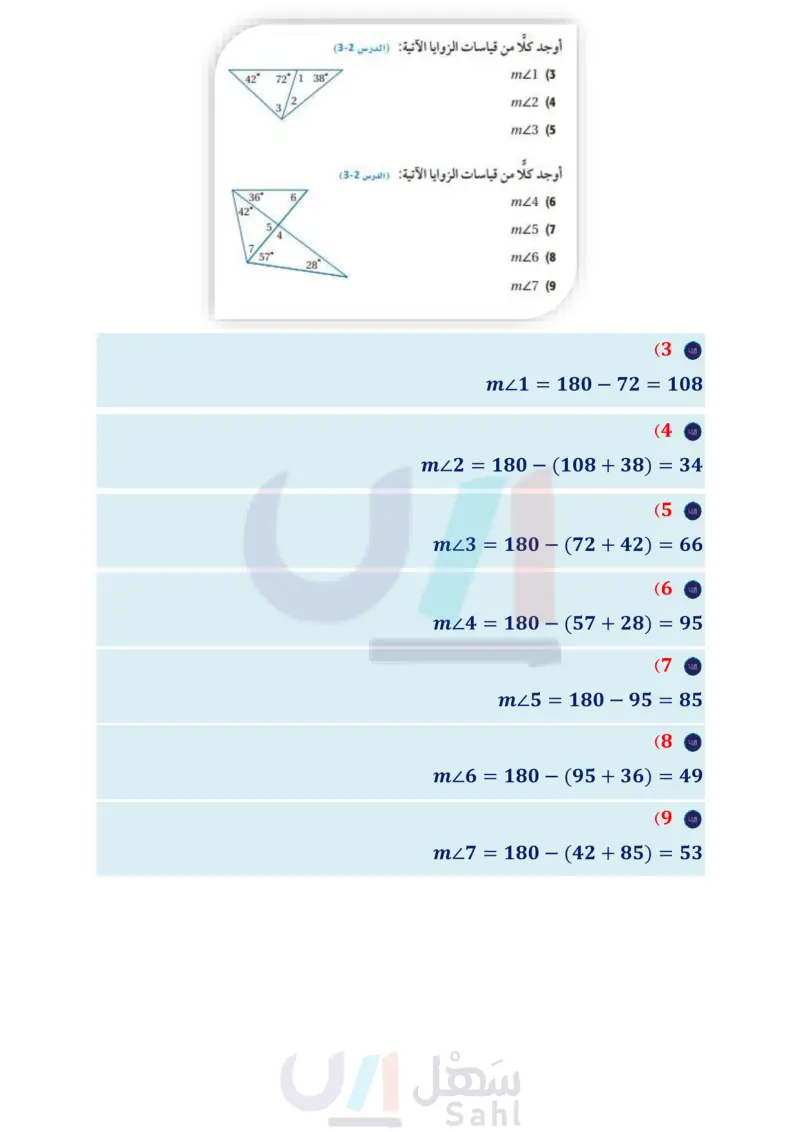
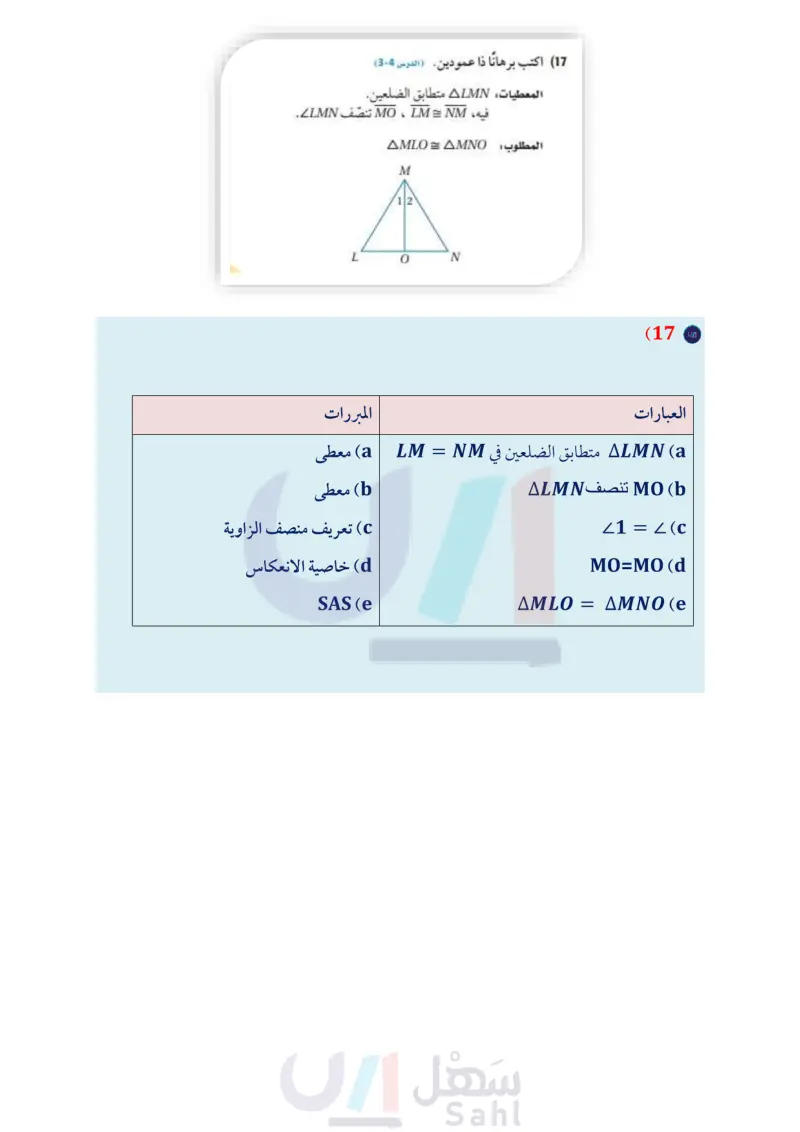
A B C D G E F H M I I K L N OPQR الفصل 3 اختبار منتصف الفصل الدروس من 1-3 إلى 4-3 1) هندسة إحداثية : صنّف AABC الذي رؤوسه (0 ,2) B-1, 3, C ,(1- ,2) إلى مختلف الأضلاع أو متطابق الأضلاع أو متطابق الضلعين. (مهارة سابقة) (2) اختيار من متعدد : أي مما يأتي يمثل أطوال أضلاع المثلث المتطابق " الضلعين QRS؟ (مهارة سابقة) R y + 11 3y - 1 (12) فن العمارة : يبين الشكل المجاور بيتا واجهته على شكل الحرف A ، وتظهر عليه نقاط مختلفة. افترض أن القطع المستقيمة والزوايا التي تبدو أنها متطابقة هي متطابقة فعلاً. اكتب المثلثات المتطابقة. (الدرس (3-3) (13) اختيار من متعدد : إذا كان ACBX = ASML، فأي عبارة مما يأتي صحيحة؟ (الدرس (3-3) ZXZS C ZXCBZLSM D CB=ML A XC=ML B 14 جسور يُظهر الجسر في الشكل أدناه أن AC 1 BD ، وأن B نقطة منتصف .AC. ما الطريقة التي يمكن استعمالها لإثبات أن ABD = ACBD ( الدرس (4-3) A B C حدد ما إذا كان APQR = AXYZ في كلُّ من السؤالين الآتيين: (الدرس 4-3) وزارة التعليم Ministry of Education 2024-1446 P(3, 5), Q(11, 0), R(1, 6), X(5, 1), Y(13, 6), Z(3, 12) (15 P(-3, -3), Q(-5, 1), R(-2, 6), X(2, -6), Y(3, 3), (16 Z(5,-1) اكتب برهانا ذا عمودين (الدرس 4-3) المعطيات: ALMN متطابق الضلعين. فيه MO ، MNM تنصف LMN. المطلوب : AMLO = AMNO M 12 L 0 N 4y-9 S 42 72/1 38° 36° 6. 42° 4 57° 28° 17, 17, 15 A 15, 15, 16 B 14, 15, 14 C 14, 14, 16 D أوجد كلا من قياسات الزوايا الآتية: (الدرس (2-3) mZ1 (3 mz2 (4 m23 (5 أوجد كلًا من قياسات الزوايا الآتية: (الدرس 2-3) mZ4 (6 m25 (7 m26 (8 m27 (9 في الشكلين أدناه، إذا علمت أن ARST = AABC فأوجد: (الدرس (3-3) (17 (51+20) R C y + 13 B S 2y-8 T A (3.x +40)° (10) قيمة . 11) قيمة . الفصل 3 المثلثات المتطابقة 44