البرهان غير المباشر - رياضيات 1-2 - أول ثانوي

4-4 فيما سبق درست البراهين الحرة وذات العمودين والتسلسلية. والان " البرهان غير المباشر Indirect Proof الماذا؟ أعلن محل أحذية عن تخفيض مقداره 25% على جميع القطع الموجودة في المحل، فسألت هند أختها مها خلال تسوقهما في المحل قائلة: إذا كان ثمن القطعة 80 ريالًا بعد التخفيض، فهل كان ثمن القطعة أكثر من 100 ريال قبل التخفيض؟ فأجابت مها : نعم؛ لأنه لو كان ثمن القطعة قبل التخفيض 100 ريال أكتب براهين جبرية غير أو أقل، فإن ثمنها بعد التخفيض سيكون 75 ريالاً أو أقل. مباشرة. غير مباشرة. المفردات: www.ien.edu.sa تخفيضات % ٢٥ أكتب براهين هندسية البرهان الجبري غير المباشر: البراهين التي كتبتها حتى الآن استعملت فيها التبرير المباشر، حيث كنت تبدأ بمعطيات صحيحة وتثبت أن النتيجة صحيحة هذه الطريقة من البرهان تعتبر برهانا مباشرًا، وعندما تستعمل التبرير غير المباشر فإنك تفترض أن النتيجة خطأ، ثم تبيّن أن هذا الافتراض يؤدي إلى تناقض مع المعطيات أو مع أي حقيقة سابقة كتعريف، أو مسلمة، أو نظرية. وحيث إن جميع خطوات البرهان تكون صحيحة منطقيا، فإنّ هذا يكون إثباتًا لخطأ الافتراض، وعلى ذلك يجب أن تكون النتيجة الأصلية صحيحةً، ويسمى هذا النوع من البرهان برهانا غير مباشر أو برهانا بالتناقض والخطوات التالية تلخص عملية البرهان غير المباشر. التبرير المباشر direct reasoning البرهان المباشر direct proof التبرير غير المباشر indirect reasoning البرهان غير المباشر indirect proof البرهان بالتناقض proof by contradiction مفهوم أساسي خطوات كتابة البرهان غير المباشر أضف إلى مطويتك الخطوة 1: حدّد النتيجة التي ستبرهنها. ثم افترض خطأها، وذلك بافتراض أن نفيها صحيح. الخطوة 2: استعمل التبرير المنطقي لتبين أن هذا الافتراض يؤدي إلى تناقض مع المعطيات أو مع حقيقة أخرى، مثل تعريف أو مسلمة أو نظرية. الخطوة 3: بما أن الافتراض الذي بدأت به أدّى إلى تناقض فبيّن أن النتيجة الأصلية المطلوب إثباتها يجب أن تكون صحيحة. مثال 1 صياغة افتراض للبدء في برهان غير مباشر اكتب الافتراض الضروري الذي تبدأ به برهانا غير مباشر لكل عبارة مما يأتي : ZABC ZXYZ (a الافتراض هو : ABC = XYZ إذا كان العدد 6 عاملًا للعدد n ، فإن 2 عامل للعدد n . نتيجة هذه العبارة الشرطية هي 2 عامل للعدد 1 ، ونفي هذه النتيجة هو 2 ليس عاملا للعدد 1 ؛ لذا فالافتراض هو العدد 2 ليس عاملا للعدد n . 3 زاوية منفرجة. الافتراض هو : 23 ليست زاوية منفرجة. تحقق من فهمك x>5 (1A AXYZ C متطابق الأضلاع. (18) النقاط تقع على استقامة واحدة. الدرس 44 البرهان غير المباشراة ال107م Ministry of Educa 2024-1446

قراءة الرياضيات التناقض التناقض مبدأ في المنطق ينص على يمكن أن تُستعمل البراهين غير المباشرة لإثبات صحة المفاهيم الجبرية. مثال 2 كتابة برهان جبري غير مباشر اكتب برهانا غير مباشر لتبين أنه إذا كان 16 4 + x 3 ، فإن 4- > x أنه لا يمكن تحقق الافتراض ونفيه في آن واحد. المعطيات : 16 - 4 + x 3 المطلوب : إثبات أن 4 > x برهان غير مباشر 108 الخطوة 1 نفي 4 > x هو -4 x ؛ لذا افترض أن 4 = x صحيحة. الخطوة 2 : x> -4 -3x12 -3x+4≤12 +4 -3x + 4 < 16 افترض اضرب الطرفين بـ 3 اجمع 4 للطرفين بسط ولكن 16 - 4 + 3x- معطى الخطوة 3 الافتراض يؤدي إلى تناقض مع المعلومة المعطاة 416 + x 3 ؛ لذا فالافتراض بأن 4 2 x يجب أن يكون خطأ، وأن النتيجة الأصلية 4 - > x هي الصحيحة. تحقق من فهمك اكتب برهانا غير مباشر لكل من العبارتين الآتيتين: 2 إذا كانت 56 < 7x ، فإن 8 < x (28) إذا كان - موجبًا ، فإنّ ، سالبٌ . ويمكنك أن تستعمل البرهان غير المباشر في المواقف الحياتية اليومية. مثال 3 من واقع الحياة استعمال البرهان الجبري غير المباشر تسوق اشترى فهد قميصين بأكثر من 60 ريالًا، وبعد عدة أسابيع سأله صديقه حامد عن ثمن كل قميص، ولكن فهذا لم يتذكر ثمن كل قميص. استعمل البرهان غير المباشر لتبين أن أحد القميصين على الأقل ثمنه أكثر من 30 ريالا. المعطيات: ثمن القميصين معا أكثر من 60 ريالًا. 60 < x + y ، حيث x ثمن القميص الأول، ولا ثمن القميص الثاني. المطلوب : إثبات أن قميصا واحدًا على الأقل ثمنه أكثر من 30 ريالًا؛ أي 30 < x أو 30 < y برهان غير مباشر الخطوة 1: افترض أن ثمن كلّ من القميصين لا يزيد على 30 ريالًا، أي أن 30 = x = 30, y الخطوة 2: إذا كانت 30 = x 30, y ، فإن 30 + 30 = x + y ؛ أي 60 = x + y . وهذا تناقض، لأن ثمن القميصين معا أكثر من 60 ريالًا. الخطوة 3: بما أن الافتراض أدّى إلى تناقض مع حقيقة معلومة، فإن الافتراض بأن 30 = x = 30, y خطأ. لذا يجب ، أن يكون ثمن أحد القميصين على الأقل أكثر من 30 ريالًا. افتراض تحقق من فهمك (3) رحلة قطع رياض أكثر من 360 كيلومترًا في رحلة، وتوقف في أثناء سفره مرتين فقط. استعمل البرهان غير المباشر لإثبات أن رياضًا قطع أكثر من 120 كيلومترًا في إحدى مراحل رحلته الثلاث على الأقل. الفصل 4 العلاقات في المثلث وزارة التعليم Ministry of Education 2024-1446

إرشادات للدراسة نظرية الأعداد هي فرع من فروع الرياضيات تختص بدراسة الأعداد وخصائصها والعمليات عليها وتصنيفها إلى زوجي فردي أولي غير أولي.... وتثبت النظريات والحقائق لهذه الأعداد. تُستعمل البراهين غير المباشرة عادة لإثبات مفاهيم في نظرية الأعداد، ويكون من المفيد في هذه البراهين تذكر أنه يمكنك تمثيل العدد الزوجي على الصورة 2 ، والعدد الفردي على الصورة + 2 حيث ، عدد صحيح. مثال 4 براهين غير مباشرة في نظرية الأعداد اكتب برهانا غير مباشر لإثبات أنه إذا كان 2 + x عددًا زوجيا، فإنّ ته عدد زوجي. المعطيات: 2 + x عدد زوجي. المطلوب : x عدد زوجي. برهان غير مباشر : الخطوة 1: افترض أن x عدد فردي ، وهذا يعني أن 1 + 2 = x ، حيث عدد الخطوة 2 x + 2 = (2 + 1) + 2 =(2k+2)+1 = 2(k + 1) + 1 عوض خاصية الإبدال خاصية التوزيع صحيح. تنبيه البرهان بالتناقض مقابل المثال المضاد البرهان بالتناقض واعطاء مثال مضاد أمران مختلفان؛ إذ يستعمل المثال المضاد لإثبات خطأ تخمين أو افتراض، ولا يمكن استعماله لإثبات صحة التخمين أو الافتراض والآن حدد ما إذا كان (2) عددًا زوجيًا أو فرديًا. بما أن k عدد صحيح، فإن 1 + k عدد صحيح أيضًا. افترض أن m تساوي 1 + k ، فيكون: 2(k+1)+1=2m+1 عوض إذن 2 + x يمكن أن يُمثل بـ 1 + 2m ، حيث m عدد صحيح ، ولكن هذا التمثيل يعني أ أن 2 + x عدد فردي. وهذا يتناقض مع العبارة المعطاة 2 + x عدد زوجي. الخطوة 3: بما أن افتراض x عدد فردي أدى إلى تناقض مع العبارة المعطاة، فإن النتيجة الأصلية x عدد زوجي يجب أن تكون صحيحة. تحقق من فهمك 4) اكتب برهانا غير مباشر لإثبات أنه إذا كان مربع عدد صحيح فرديا، فإن العدد الصحيح فردي“. البرهان غير المباشر في الهندسة : يمكن أن يستعمل التبرير غير المباشر لإثبات صحة عبارات في الهندسة، مثل نظرية متباينة الزاوية الخارجية. مثال 5 برهان هندسي أثبت أن قياس الزاوية الخارجية لمثلث يكون أكبر من قياس كلِّ من الزاويتين الداخليتين البعيدتين عنها. ارسم شكلا توضيحيا، ثم عين عليه المعطيات والمطلوب. المعطيات : 4 زاوية خارجية لـ AABC . المطلوب : إثبات أن m4 > m2 ، وأن 1 m4 > m . برهان غير مباشر الخطوة 1 : افترض أن m4 m1 ، أو m4 7 m2 . أي أن m24 = m1، أو m4 ≤ m2 . A .B C الدرس 4-4 البرهان غير المباشر ال109 Ministry of Edu 2024-1446

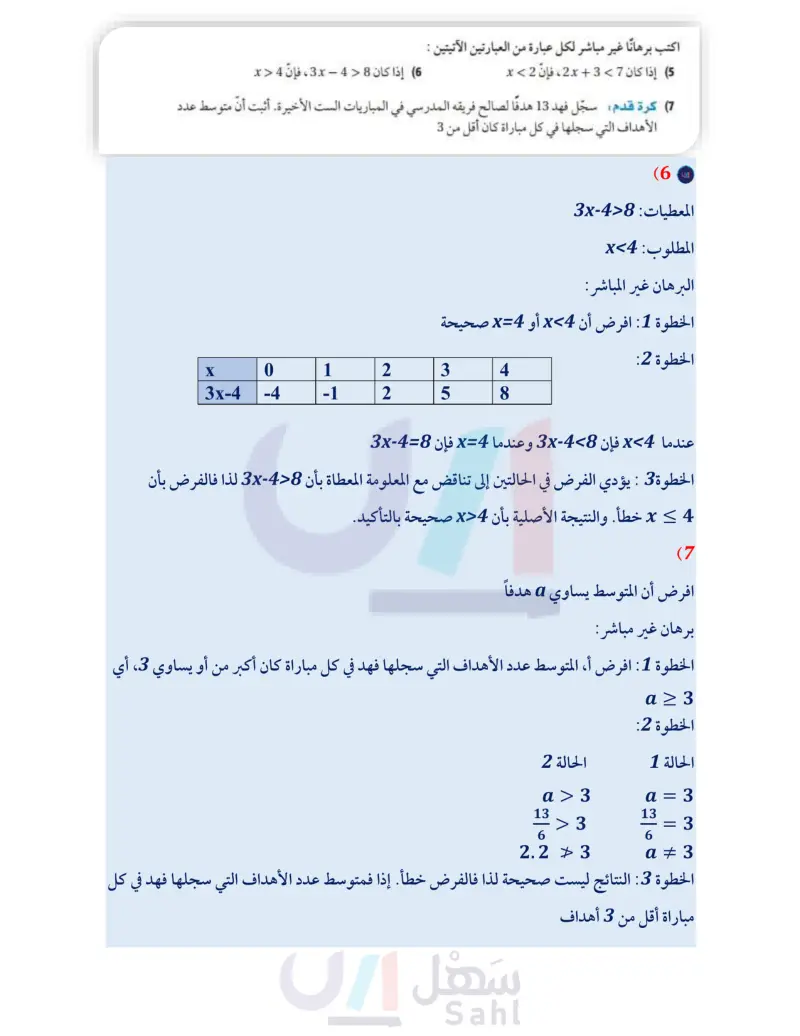
الخطوة 2: تحتاج فقط إلى بيان أن الافتراض m4 = m1 يؤدي إلى تناقض، وبالمثل سيؤدي الافتراض m2 = m4 إلى تناقض أيضًا. الافتراض m4 = m1 يعني أن : m4 = m1 أو m4 < m1 . الحالة 1: mZ4 = mZ1 mZ4 = mZ1 + m22 mZ4 = mZ4 + m2 0 = m2 نظريه الزاوية الخارجية عوض اطرح m4 من كلا الطرفين. وهذا يناقض حقيقة أن قياس الزاوية أكبر من 0؛ لذا فإن m4 + m1 . إرشادات للدراسة تعرف التناقضات تذكر أن التناقض في البرهان غير المباشر لا يكون دائما مع المعطيات أو الفرض الذي تبدأ به الحالة 2 : mZ4 <mZ1 mZ4 = mZ1 + m22 mZ4 > mZ1 نظرية الزاوية الخارجية قياسات الزوايا موجبة هذا يناقض الفرض بأن m4 < m1 الخطوة 3: في الحالتين يؤدي الافتراض إلى تناقض مع نظرية أو تعريف؛ لذا فالنتيجة الأصلية بأنّ m4 > m2 وأن 1 4 يجب أن تكون صحيحة. بل يمكن أن يكون مع حقيقة معلومة أو تعريف كما ورد في الحالة 1 من المثال 5 ، حيث إن قياس تحقق من فهمك أي زاوية في مثلث يجب أن يكون أكبر من 0 (5) اكتب برهانا غير مباشر. 110 المعطيات : MO = ON, MP # NP المطلوب LMOP # LNOP P N M تأكد المثال 1 اكتب الافتراض الذي تبدأ به برهانا غير مباشر لكل عبارة مما يأتي : AB = CD (1 (3) إذا كان 24 > 4x ، فإن 6 > x المثال 2 اكتب برهانا غير مباشر لكل عبارة من العبارتين الآتيتين : إذا كان 7 > 3 + 2x ، فإن 2 > x (2) AXYZ مختلف الأضلاع. ليست زاوية قائمة. (6) إذا كان 8 × 4 - 3x ، فإن 4 < x المثال 3 (7) كرة قدم: سجّل فهد 13 هدفًا لصالح فريقه المدرسي في المباريات الست الأخيرة. أثبت أن متوسط عدد الأهداف التي سجلها في كل مباراة كان أقل من 3 المثال 4 8 اكتب برهانا غير مباشر لإثبات أنه إذا كان 2 - 5x عددًا فرديًا، فإن x عدد فردي. المثال 5 اكتب برهانا غير مباشر لكل عبارة من العبارتين الآتيتين: (9) وتر المثلث القائم الزاوية هو أطول أضلاعه. (10) إذا كانت الزاويتان متكاملتين، فإنّه لا يمكن أن تكونا منفرجتين معا. الفصل 4 العلاقات في المثلث وزارة التعليم Ministry of Education 2024-1446

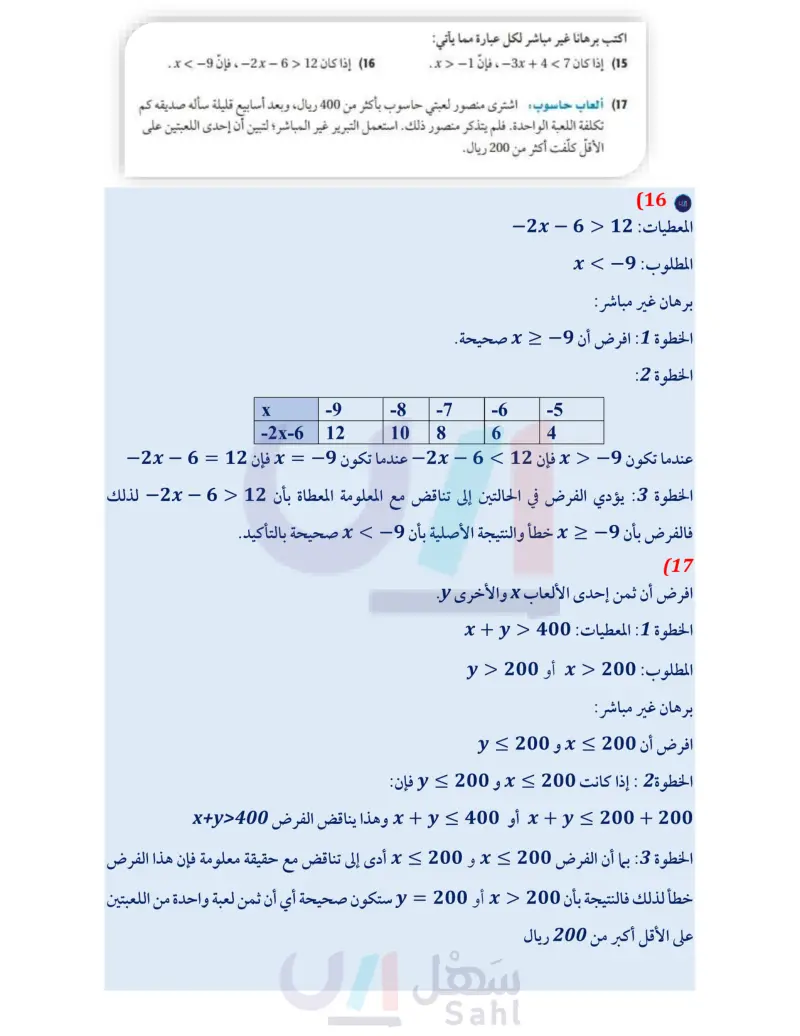
تدرب وحل المسائل المثال 1 اكتب الافتراض الذي تبدأ به برهانا غير مباشر لكل عبارة مما يأتي: (11) إذا كان 16 < 2x ، فإن 8 < x . 12 122 زاويتان غير متكاملتين (13) إذا تساوى ميلا مستقيمين فإن المستقيمين متوازيان. (14) العدد الفردي لا يقبل القسمة على 2 . المثال 2 اكتب برهانا غير مباشر لكل عبارة مما يأتي: (15) إذا كان 7 4 + 3x- ، فإن 1- < x . 16 إذا كان 12 - 6 - 2x ، فإن 9- > x . المثال 3 17) ألعاب حاسوب: اشترى منصور لعبتي حاسوب بأكثر من 400 ريال، وبعد أسابيع قليلة سأله صديقه كم تكلفة اللعبة الواحدة. فلم يتذكر منصور ذلك استعمل التبرير غير المباشر؛ لتبين أن إحدى اللعبتين على الأقل كلفت أكثر من 200 ريال. 18 جمع التبرعات: أقامت جمعية خيرية حفلة لجمع التبرعات لمساعدة الفقراء والمحتاجين، وكان سعر تذكرة الدخول للكبار 30 ريالًا، وللأطفال 12.5 ريالًا. إذا بيعت 375 تذكرة، وكان ريعها أكثر من 7300 ريال، فأثبت أنه تم بيع ا 150 تذكرة على الأقل للكبار المثالان 45 اكتب برهانا غير مباشر لكل عبارة مما يأتي: 19) المعطيات: xy عدد صحيح فردي. المطلوب : كلًا من x, y عدد صحيح فردي (21) المعطيات : XZ > YZ المطلوب : XY (20) المعطيات: n2 عدد زوجي. المطلوب: 1 عدد زوجي. (22) المعطيات: AABC متطابق الأضلاع المطلوب : AABC متطابق الزوايا. B A C Y X Z الربط مع الحياة هناك أكثر من طريقة لتسجيل ثلاث نقاط في (23) اكتب برهانا غير مباشر لإثبات أنه لا يمكن أن يكون للمثلث أكثر من زاوية قائمة. (24) اكتب برهانا غير مباشر للنظرية 4.10. 25) اكتب برهانا غير مباشر لإثبات أنه إذا كان 0 > ، فـ ، فإن 6 عدد سالب. كرة السلة، منها التسجيل 26) كرة سلة : عندما خرج عدنان من الملعب ليدخل زميل له قبيل نهاية الشوط الأول من المباراة كان فريق من خارج المنطقة، ومنها أن يسجل اللاعب نقطتين ويحصل على رمية حرة نتيجة خطأ من الفريق المنافس ويسجل منها نقطة. مدرسته متقدّمًا بـ 28 نقطة مقابل 26 . وعندما عاد مع بداية الشوط الثاني كان الفريق المنافس متقدما بـ 29 نقطة مقابل 28 نقطة. استنتج أخو عدنان حين علم ذلك أن لاعبًا من الفريق المنافس سجل ثلاث نقاط من رمية واحدة. أثبت صحة أو خطأ استنتاجه باستعمال البرهان غير المباشر ومعلومات الربط مع الحياة. الدرس 4-4 البرهان غير المباشرة ال111 Ministry of E 2024-1446

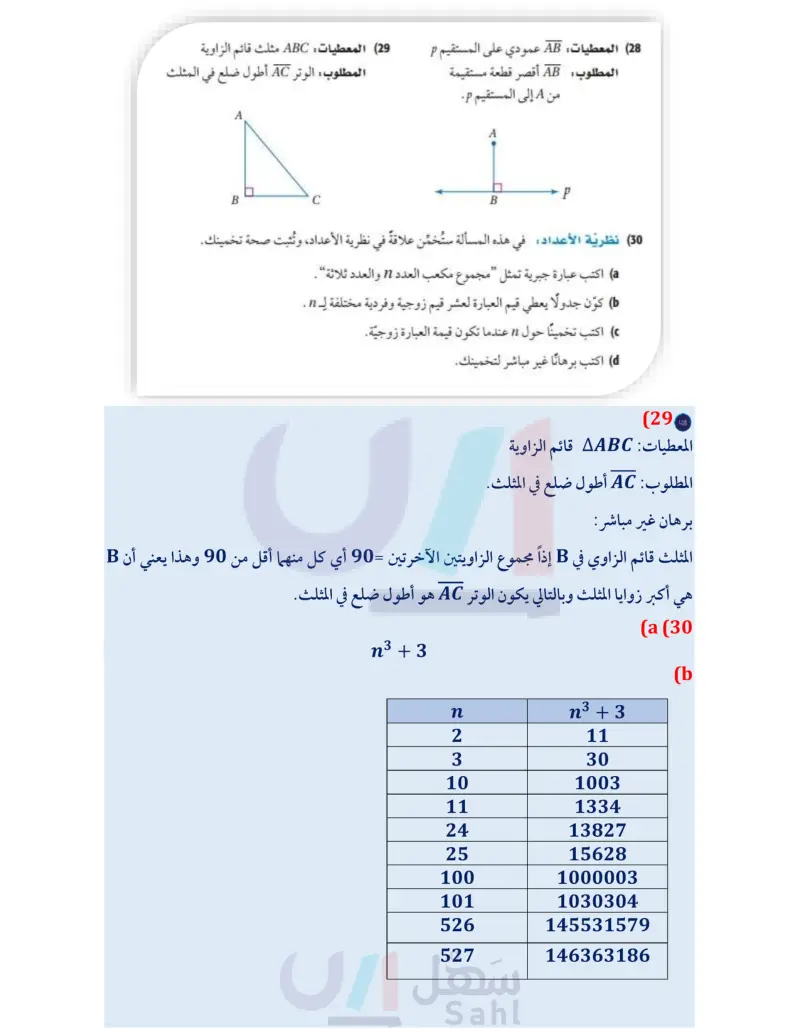
وزارة التعليم Ministry of Education 2024-1446 27) ألعاب إلكترونية تتضمن لعبة حاسوبية فارسًا في رحلةٍ للبحث عن الكنز، وفي نهاية الرحلة يقترب الفارس من البابين المبينين أدناه. أحد هذين البابين يؤدي إلى تنين يوجد خلف هذا الباب كنز وخلف الباب الآخر تنين. 9 أخبر خادم الفارس بأن أحد الإعلانين . والآخر خطأ. استعمل التبرير غير المباشر لتحدد أي البابين سيختاره الفارس. وضح إجابتك. حدد ما إذا كان إثبات كل عبارة حول أقصر مسافة بين نقطة وخط مستقيم أو مستو، يمكن إثباتها باستعمال البرهان المباشر أو البرهان غير المباشر، ثم اكتب برهانا لكل منهما. 28 المعطيات: AB عمودي على المستقيم P (29) المعطيات ABC مثلث قائم الزاوية المطلوب: الوتر AC أطول ضلع في المثلث المطلوب : AB أقصر قطعة مستقيمة من A إلى المستقيم p . A B C A P B (30) نظرية الأعداد في هذه المسألة ستُخمّن علاقةً في نظرية الأعداد، وتثبت صحة تخمينك. اكتب عبارة جبرية تمثل مجموع مكعب العدد 1 والعدد ثلاثة . كوّن جدولا يعطي قيم العبارة لعشر قيم زوجية وفردية مختلفة لـ n . اكتب تخمينا حول n عندما تكون قيمة العبارة زوجية. اكتب برهانا غير مباشر لتخمينك. مراجعة المفردات مجموعة الأعداد الصحيحة هي : {..., -2, -1, 0, 1, 2, ...} مسائل مهارات التفكير العليا 31) مسألة مفتوحة اكتب عبارة يمكن إثبات صحتها باستعمال البرهان غير المباشر ثم أثبتها. (32) تحد : إذا كان x عددًا نسبيا، فإنه يمكن تمثيله بالصورة ، حيث عددان صحيحان، و 0 # b . ولا يمكن تمثيل العدد غير النسبي في صورة ناتج قسمة عددين صحيحين اكتب برهانا غير مباشر تبين فيه أن ناتج ضرب عدد نسبي لا يساوي الصفر في عدد غير نسبي، هو عدد غير نسبي. الفصل 4 العلاقات في المثلث 112

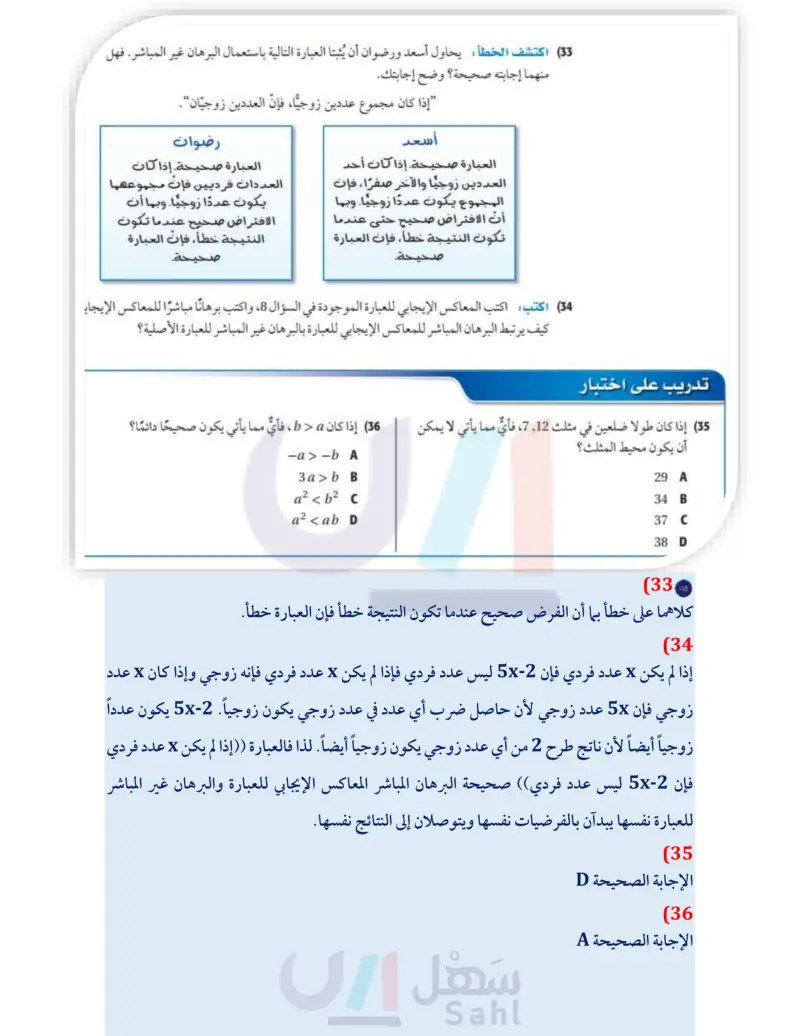
S A (33) اكتشف الخطأ يحاول أسعد ورضوان أن يُثبتا العبارة التالية باستعمال البرهان غير المباشر. فهل أي منهما إجابته صحيحة ؟ وضح إجابتك. إذا كان مجموع عددين زوجيا، فإن العددين زوجيّان. أسعد العبارة صحيحة. إذا كان أحد العددين زوجيا والآخر صفرًا، فإن المجموع يكون عددا زوجيا. وبما أن الافتراض صحيح حتى عندما تكون النتيجة خطأ، فإن العبارة صحيحة. رضوان العبارة صحيحة. إذا كان العددان فرديين فإن مجموعهما يكون عددا زوجيا. وبما أن الافتراض صحيح عندما تكون النتيجة خطأ، فإن العبارة صحيحة. (34) اكتب اكتب المعاكس الإيجابي للعبارة الموجودة في السؤال ،8، واكتب برهانا مباشرًا للمعاكس الإيجابي كيف يرتبط البرهان المباشر للمعاكس الإيجابي للعبارة بالبرهان غير المباشر للعبارة الأصلية؟ R تدريب على اختبار 35) إذا كان طولا ضلعين في مثلث 12, 7، فأي مما يأتي لا يمكن 36) إذا كان b > a ، فأي مما يأتي يكون صحيحًا دائما؟ Q T 2/ /3 B F 64 F D -a-b A 3ab B a² <b² c a² <ab D أن يكون محيط المثلث ؟ 29 A 34 B 37 C 38 D مراجعة تراكمية (37) برهان اكتب برهانا ذا عمودين (الدرس (3-4) المعطيات RQ تنصف SRT . المطلوب : إثبات أن mLSQR > mLSRQ أوجد كلا من القياسين الآتيين : (الدرس (2-3) m21 (38 m/4 (39 (40) هندسة إحداثية : أوجد المسافة بين المستقيمين المتوازيين: (مهارة سابقة) 3x + 54 < 90 (43) 8x - 14 < 3x + 19 42 الدرس 4-4 البرهان غير المباشرا ال113 Ministry of Educ 2024-1446 y = 2x + 2 y = 2x - 3 استعد للدرس اللاحق حُلَّ كلًّا من المتباينات الآتية: 4x + 7 < 180 (41)