المثلثات والبرهان الإحداثي - رياضيات 1-2 - أول ثانوي
الفصل3: المثلثات المتطابقة
الفصل4: العلاقات في المثلث
الفصل5: الأشكال الرباعية
نشاط الفصل 3: المثلثات المتطابقة
نشاط الفصل 4: العلاقات في المثلث
نشاط الفصل 5: الأشكال الرباعية
المثلثات والبرهان الإحداثي Triangles and Coordinate Proof 3-7 فيما سبق : درست استعمال الهندسة الإحداثية لبرهان تطابق المثلثات. (مهارة سابقة ) والان - أرسم مثلثات، وأحدد البرهان الإحداثي. أكتب برهانا إحداثيا الملادارة نظام تحديد الموقع العالمي (GPS) يستقبل البث من الأقمار الاصطناعية، والتي يمكن بواسطتها تحديد موقع السيارة. ويمكن الاستفادة من هذه المعلومات بالإضافة إلى برمجيات أخرى لتوجيه حركة السيارة. مواقعها لاستعمالها في موقع المثلث وتسميته كما هو الحال في نظام تحديد الموقع العالمي، فإن معرفة إحداثيات رؤوس شكل ما في مستوى إحداثي، يمكنك من اكتشاف خصائصه والتوصل إلى استنتاجات خاصة به. ويستعمل البرهان الإحداثي الأشكال في المستوى الإحداثي والجبر لإثبات صحة المفاهيم الهندسية. فالخطوة الأولى في البرهان الإحداثي هي تمثيل الشكل في المستوى الإحداثي. المفردات: البرهان الإحداثي coordinate proof إرشادات للدراسة الارتفاع على القاعدة في المثلث المتطابق الضلعين ينصف القاعدة. مثال 1 تحديد موقع المثلث وتسميته ارسم المثلث القائم MNP في المستوى الإحداثي، وسمّ رؤوسه على أن يكون طول MN يساوي a وحدة، وطول NP يساوي 6 وحدة. . يُحدد طول الضلع الذي يقع على أحد المحورين بسهولة؛ لذا من الأفضل وضع ضلعي القائمة على المحورين x,y. . اجعل زاوية المثلث القائمة N على نقطة الأصل، فيكون ضلعا القائمة على المحورين هما x y . . ارسم المثلث في الربع الأول. M(0, a) P(b, 0) ON(0, 0) x . ارسم على المحور y ، وبما أن طول MN يساوي a وحدة، فإن إحداثيها x يساوي صفرًا، وإحداثيها لا يساوي .. . ارسم P على المحور x ، وبما أن طول NP يساوي 6 وحدة، فإن إحداثيها لا يساوي صفرا، وإحداثيها تx يساوي b. تحقق من فهمك 1) ارسم المثلث JKL المتطابق الضلعين في المستوى الإحداثي وسمٌ ،رؤوسه، على أن يكون طول قاعدته IL يساوي a وحدة، ويكون ارتفاعه 6 وحدة، والرأس K يقع على المحور y. 62 الفصل 3 المثلثات المتطابقة مفهوم أساسي رسم المثلثات في المستوى الإحداثي الخطوة 1: اجعل نقطة الأصل رأسًا للمثلث. الخطوة 2 ارسم ضلعا واحدًا على الأقل من أضلاع المثلث على أ الخطوة 3: ارسم المثلث في الربع الأول إن أمكن. أحد المحورين الخطوة 4: استعمل الإحداثيات التي تجعل الحسابات أبسط ما يمكن. أضف إلى مطويتك وزارة التعليم Ministry of Education 2024-1446

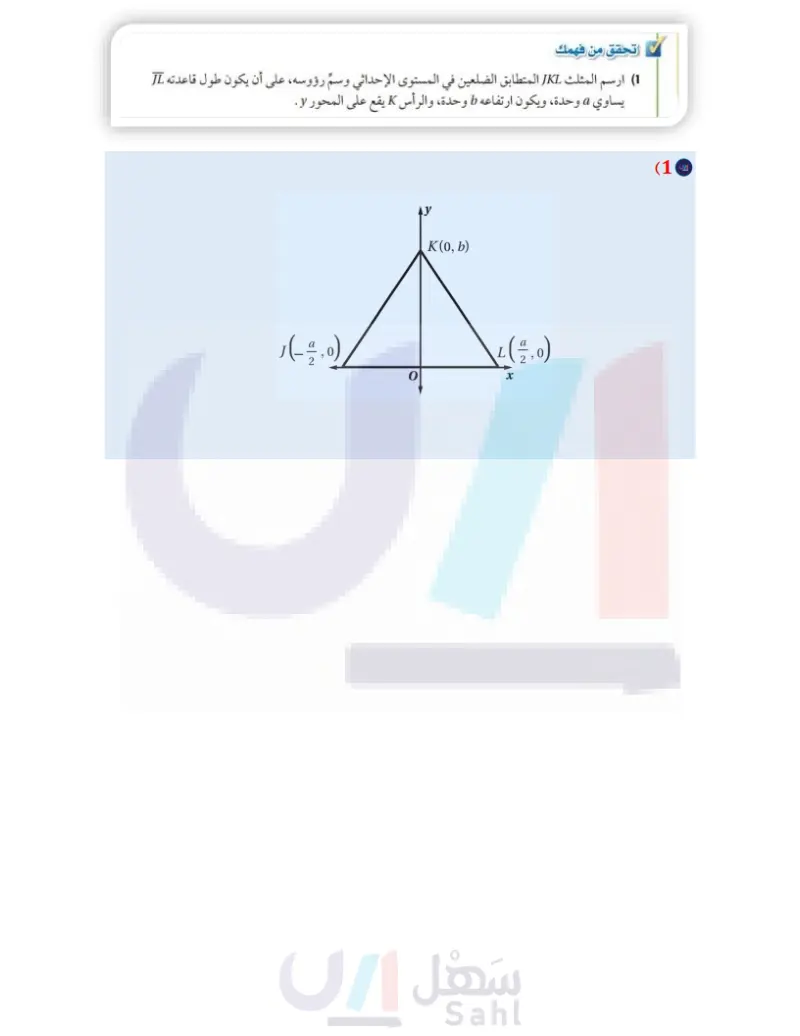
ارسم المثلث JKL المتطابق الضلعين في المستوى الإحداثي وسمّ روؤسه، على أن يكون طول قاعدته JL يساوي a وحدة.


الارتفاع على القاعدة في المثلث المتطابق الضلعين ينصف القاعدة
إرشادات للدراسة الزاوية القائمة تقاطع المحور x مع المحور لا يشكل زاوية قائمة؛ ولذا يُعد هذا التقاطع المكان المناسب لموقع الزاوية القائمة. مثال 2 إيجاد الإحداثيات المجهولة أوجد الإحداثيات المجهولة في المثلث XYZ المتطابق الضلعين. بما أن الرأس X يقع عند نقطة الأصل، فإن إحداثياته هي (0 ,0)، ولأن الرأس Z يقع على المحور x ، فإن الإحداثي y له يساوي صفرًا، فتكون إحداثيات الرأس 2 هي ( (0) ، وبما أن AXYZ متطابق الضلعين، فإن الإحداثي x للنقطة Y يقع في منتصف المسافة بين , ويكون ، أما الإحداثي y للنقطة Y فلا يمكننا إيجاده بدلالة a ، وإذا افترضناه b ، فتكون إحداثيات النقطة Y هي (1) . تحقق من فهمك 2) أوجد الإحداثيات المجهولة في المثلث AABC المتطابق الضلعين والقائم الزاوية. Z(a,?) Y(?, ?) X(?,?) x у A (?, ?) B(?, ?) C(a,?) 0 إرشادات للدراسة البرهان الإحداثي كتابة البرهان الإحداثي بعد رسم المثلث في المستوى الإحداثي، وتحديد إحداثيات رؤوسه، يمكنك استعمال البرهان الإحداثي؛ للتحقق من بعض الخصائص وبرهنة بعض النظريات. مثال 3 كتابة البرهان الإحداثي اكتب برهانًا إحداثيا لإثبات أن القطعة المستقيمة التي تصل بين منتصفي ضلعين في مثلث توازي الضلع الثالث. اجعل أحد رؤوس المثلث عند نقطة الأصل وسمه A، واستعمل إحداثيات من مضاعفات 2 ؛ لأن قانون نقطة المنتصف يتضمن قسمة مجموع الإحداثيين على 2 المعطيات AABC ، فيه x+ B(2a, 0) C(2b, 2c) S T OA (0, 0) تنطبق الإرشادات والطرائق المستعملة في هذا الدرس على كل المضلعات ، ولا تقتصر على المثلثات. نقطة منتصف AC T نقطة منتصف BC . المطلوب : إثبات أن ST || AB . البرهان : باستعمال قانون نقطة المنتصف، فإن إحداثيات هي : ( ) 2a+2b 0+2c 2 وكذلك إحداثيات T هي: (a + b = 02 2012 وبتطبيق قانون الميل، فإن ميل ST هو: 0 = C-C a+b-b وميل AB هو: 0 = 0-0 2a-0 (2b+0 2c+0). وبما أن ميل ST يساوي ميل AB ، فإن ST || AB . الدرس 37 - المثلثات والبرهان الإحداثي الله 63 Ministry of Edu 2024-1446

البرهان الإحداثي
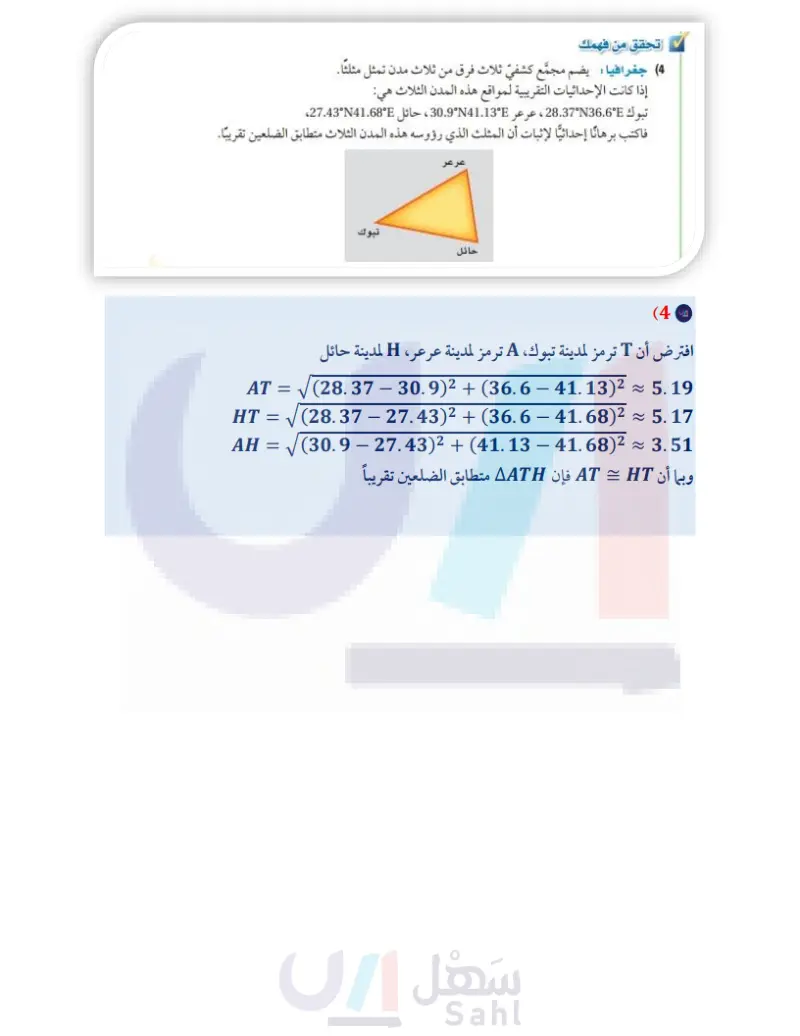
A (0, 0) B (0 + x, b C(a+x, b) D(a, 0) x T(28.37, 36.6) وزارة التعليم Ministry of Education 2024-1446 تحقق من فهمك (3) اكتب برهانا إحداثيا لإثبات أن: .AABX = ACDX المحيط الأطلسي ل برمودا يمكن استعمال طرائق البرهان الإحداثي لحل مسائل من واقع الحياة. مثلث برمودا الربط مع الحياة يقع مثلث برمودا المبين في الخريطة في المحيط الأطلسي، وهو على شكل مثلث مختلف الأضلاع وتقدر مساحته الحقيقية بـ 482344 ميلا مربعا. مثال 4 من واقع الحياة تصنيف المثلثات جغرافيا : إذا علمت أن الإحداثيات التقريبية لكلَّ من الرياض وينبع وتبوك هي: الرياض 24.15°N 46.72°E ، ينبع 24.63°N 38.07°E ، تبوك 28.37°N 36.6°E . فاكتب برهانا إحداثيا يبين أن المثلث الذي رؤوسه هذه المدن الثلاث مختلف الأضلاع. إرشاد: يمكن التعبير عن إحداثي الرياض 24.15°N 46.72°E بالزوج المرتب (24.1546.72) وكذلك بقية المدن. الخطوة الأولى هي رسم شكل تقريبي لهذا المثلث، وتعيين المواقع الثلاثة وإحداثياتها على الرسم، ولتكن R تمثل الرياض، و لا تمثل ينبع ، و T تمثل تبوك. إذا لم يتطابق أي ضلعين في ARYT ، فسيكون مختلف الأضلاع. استعمل قانون المسافة بين نقطتين والآلة الحاسبة لإيجاد أطوال أضلاع المثلث. R(24.15, 46.72) Y(24.63, 38.07) RY (24.15 24.63)2 + (46.72 - 38.07)² ≈ 8.66 RT √(28.37 24.15)2 + (36.6 - 46.72)² ≈ 10.96 YT (24.63 28.37)2 + (38.07 - 36.6)² ≈ 4.02 تاريخ الرياضيات محمد بن أحمد وبما أن أطوال أضلاع المثلث مختلفة، إذن فهو مثلث مختلف الأضلاع؛ أي أن المثلث الذي رؤوسه هي الرياض وينبع وتبوك مختلف الأضلاع. أبو الريحان البيروني الخوارزمي 973-362 برز في كثير من فروع المعرفة الإنسانية الأدب، الجغرافيا الفلك الرياضيات، فقد حدد بدقة خطوط الطول وخطوط العرض، ووضع قاعدة حسابية لتسطيح الكرة؛ أي نقل الخطوط والخرائط من الكرة إلى سطح مسطح والعكس.. تحقق من فهمك (4) جغرافيا: يضم مجمَّع كشفي ثلاث فرق من ثلاث مدن تمثل مثلثا. إذا كانت الإحداثيات التقريبية لمواقع هذه المدن الثلاث هي: تبوك 28.37°N36.6°E ، عرعر 30.9°N41.13°E ، حائل 27.43°N41.68°E، فاكتب برهانا إحداثيا لإثبات أن المثلث الذي رؤوسه هذه المدن الثلاث متطابق الضلعين تقريبا. عرعر تبوك حائل الفصل 3 المثلثات المتطابقة 64

يقع مثلث برمودا المبين في الخريطة في المحيط الأطلسي وهو على شكل مثلث مختلف الأضلاع
محمد بن أحمد أبو الريحان البيروني الخوارزمي
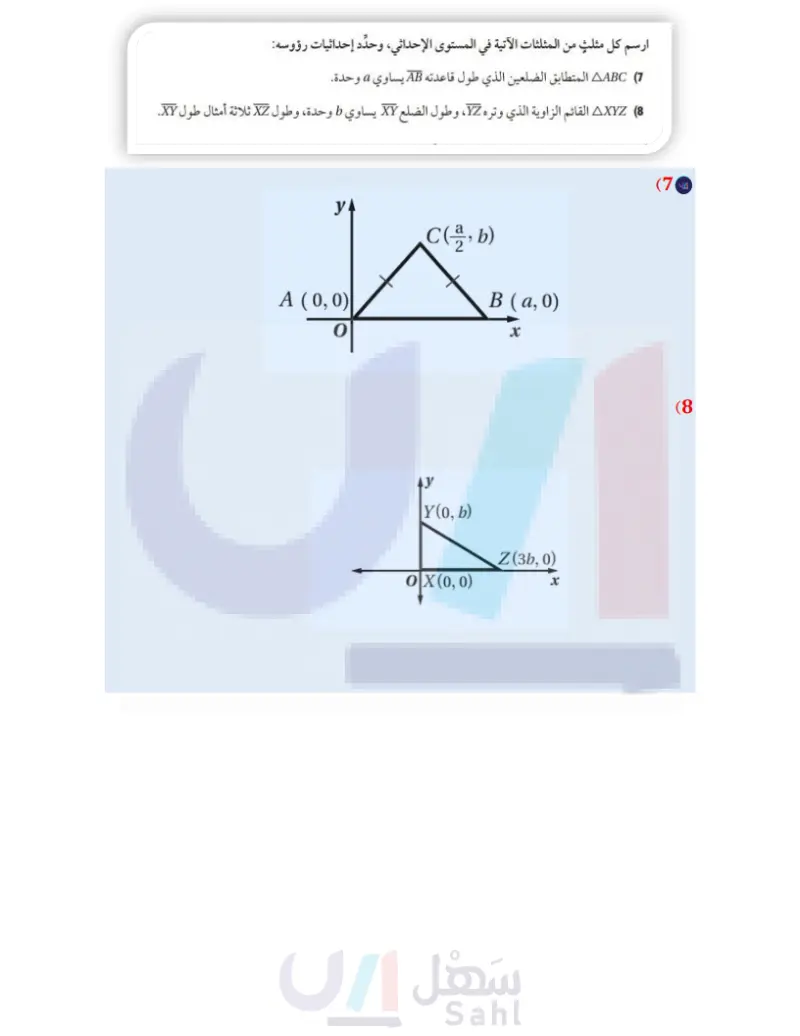
المثال 1 ارسم كلا من المثلثين الآتيين في المستوى الإحداثي، وحدد إحداثيات رؤوسه. 1) AABC قائم الزاوية، فيه A, B ضلعا القائمة، وطول AC يساوي 20 وحدة، وطول AB يساوي 20 وحدة. 2 AFGH المتطابق الضلعين الذي طول قاعدته FG يساوي 20 وحدة. المثال 2 أوجد الإحداثيات المجهولة في كل من المثلثين الآتيين: B W(?, ?) (4 Z(?, b) Y(2a, 0) R(-2a, 0) D(-a, b) C(-a, 0) (3 S (0, b) T(?,?) x المثال 3 (5) اكتب برهانًا إحداثيا لإثبات أن AFGH = AFDC. У F(0,2) G(a, b) H(a,0) x المثال 4 6 اكتب برهانًا إحداثيًا لإثبات أن المثلث ABC متطابق الضلعين، علما بأن يُعدي C المظروف هما: 10cm, cm، والنقطة B في منتصف الحافة السفلى للمظروف. تأكد تدرب وحل المسائل المثال 1 ارسم كل مثلث من المثلثات الآتية في المستوى الإحداثي، وحدد إحداثيات رؤوسه: 7) ABC المتطابق الضلعين الذي طول قاعدته AB يساوي a وحدة. 8 AXYZ القائم الزاوية الذي وتره YZ ، وطول الضلع XY يساوي 6 وحدة، وطول XZ ثلاثة أمثال طول XY. المثال 2 أوجد الإحداثيات المجهولة في كل مثلث مما يأتي: N(0,?) (11 H(?, c) (10) B(?, b) AY (9 C(?, ?) D(4b,?) K(-a, 0) P(?, 0) Z(0, 0) Y(a,?) x 이 الدرس 7-3 المثلثات والبرهان الإحداثي ال 65 Ministry of Edu 2024-1446

المثالان 34 برهان اكتب برهانًا إحداثيا لكل عبارة من العبارات الآتية: (12) القطع المستقيمة الثلاث الواصلة بين نقاط منتصفات أضلاع مثلث متطابق الضلعين تشكل مثلثاً متطابق الضلعين أيضًا. 13) طول القطعة المستقيمة الواصلة بين منتصفي ضلعين في المثلث يساوي نصف طول الضلع الثالث. (14) جغرافيا : إذا علمت أن الإحداثيات التقريبية لمواقع مدن جازان ونجران وخميس مشيط هي: جازان 42.58 16.9°N ، نجران 44.16 17.5°N ، خمیس مشیط 18.3°N 42.8°E، فبين أن المثلث الذي رؤوسه هي هذه المدن الثلاث مختلف الأضلاع في AXYZ ، أوجد ميل كل ضلع من أضلاعه، ثم حدد ما إذا كان المثلث قائم الزاوية أم لا. ووضح إجابتك. X(0, 0), Y(2h, 2h), Z(4h, 0) (15 X(0, 0), (1, h), Z(2h, 0) (16 (17) نزهة : أقامت عائلتان خيمتين في متنزه كبير . إذا اعتبرنا أن موقع إدارة المتنزه تقع عند النقطة (0,0)، وأن إحداثيات موقعي الخيمتين هما (12) (025) . فاكتب برهانًا إحداثيًا لإثبات أن الشكل المتكون من مواقع إدارة المتنزه والخيمتين هو مثلث قائم الزاوية. (18) رياضة مائية: انطلقت ثلاثة قوارب مائية من الرصيف نفسه، فاتجه الأول نحو الشمال الشرقي، واتجه الثاني نحو الشمال الغربي، أما الثالث فاتجه نحو الشمال. القارب 1 القارب 3 القارب 2 الربط مع الحياة تستثمر المنطقة الشرقية وجدة إطلالتيهما على الخليج العربي والبحر الأحمر في توجيه برامج رياضية بحرية متنوعة للسياح الذين يتوافدون على الواجهات البحرية من مختلف مناطق المملكة توقف القاربان (الأول والثاني) على بُعد 300m تقريبًا من الرصيف، بينما توقف الثالث على بعد 212m من الرصيف. ) إذا اعتبرنا أن الرصيف يمثل النقطة (0,0) ، فمثل هذا الوضع بيانيا، وأوجد معادلة خط سير القارب الأول، ومعادلة خط سير القارب الثاني. وفسّر إجابتك. ) اكتب برهانا حرا لإثبات أن الرصيف والقاربين (الأول والثاني) تُشكل مثلثا قائم الزاوية متطابق الضلعين. أوجد إحداثيات مواقع هذه القوارب الثلاثة، وفسّر إجابتك. مسائل مهارات التفكير العليا اكتب برهانًا إحداثيا لإثبات أن القوارب الثلاثة تقع على خط مستقيم واحد تقريبا، وأن القارب الثالث يقع في منتصف المسافة بين القاربين الأول والثاني. تحد: إذا كانت إحداثيات النقطة ) . هي (0 ,0)، والنقطة K هي (2) ، فأوجد إحداثيات النقطة ، على أن يكون AJKL من النوع المحدّد في كل من الأسئلة الثلاثة الآتية: (19) مثلث مختلف الأضلاع 20 مثلث قائم الزاوية (21) مثلث متطابق الضلعين (22) مسألة مفتوحة في المستوى الإحداثي، ارسم مثلثاً قائم الزاوية متطابق الضلعين، على أن تكون نقطة نقطة منتصف وتره، وحدد إحداثيات كل رأس من رؤوسه. الأصل هي 66 الفصل 3 المثلثات المتطابقة وزارة التعليم Ministry of Education 2024-1446

تستثمر المنطقة الشرقية وجدة إطلالتيهما على الخليج العربي والبحر الأحمر في توجيه برامج رياضية بحرية متنوعة للسياح الذين يتوافدون على الواجهات البحرية من مختلف مناطق المملكة
تدريب على اختبار (23) تبرير: إحداثيات رأسين في مثلث هما (0) (0) . إذا أعطي إحداثي الرأس الثالث بدلالة a ، وكان المثلث متطابق الضلعين، فحدّد إحداثيات الرأس الثالث ، ثم ارسم المثلث في المستوى الإحداثي. 24) اكتب وضح فائدة اتباع كل من الإرشادات الآتية؛ لرسم المثلث في المستوى الإحداثي عند كتابة البرهان الإحداثي : a اجعل نقطة الأصل أحد رؤوس المثلث. (b ارسم . ضلعا واحدًا على الأقل من أضلاع المثلث على المحور x أو المحور y. حاول أن يقع المثلث في الربع الأول ما أمكن ذلك. (25) في الشكل أدناه إذا كان "76" = mLB، وقياس A يساوي (26) ما إحداثيات النقطة R نصف قیاس ،B ، فما mLC؟ في المثلث المجاور؟ P(0, 0) Q(2a, 0) x (4a, b) C (a, b) B 46° (C 66° (D 33° (A 38° (B مراجعة تراكمية باستعمال الشكل المجاور، أجب عن الأسئلة 29-27 الدرس 6-3 (27 سم زاويتين متطابقتين غير المشار إليهما في الشكل. 28) سم قطعتين مستقيمتين متطابقتين غير المشار إليهما في الشكل. (29) سم مثلثين متطابقين. 30) ما ميل المستقيم المار بالنقطتين (26) (2) (مهارة سابقة) استعد للدرس اللاحق أوجد المسافة بين كل زوج من النقاط الآتية، وقرب الناتج إلى أقرب عُشر : X(5, 4), (2, 1) (31 A(1, 5), B(-2,-3) (32 J(-2, 6), K(1, 4) (33 R V T Q # S الدرس - المثلثات والبرهان الإحداثي الت 67 Ministry of Edu 2024-1446

الفصل 3 دليل الدراسة والمراجعة ملخص الفصل مفاهيم أساسية تصنيف المثلثات الدرس (1-3) المفردات الأساسية : المثلث الحاد الزوايا (ص. (12) النتيجة (ص. (23) المثلث المنفرج الزاوية (ص 12) التطابق (ص. (28) المثلث القائم الزاوية (ص. (12) المضلعات المتطابقة (ص 28) . يمكن تصنيف المثلث بحسب نوع زواياه، فيكون حاد الزوايا المثلث المتطابق الأضلاع (ص. (13) العناصر المتناظرة (ص 28) أو متطابق الزوايا أو منفرج الزاوية أو قائم الزاوية. وكذلك المثلث المتطابق الضلعين (ص. (13) الزاوية المحصورة (ص 38) يمكن تصنيفه بحسب أضلاعه، فيكون مختلف الأضلاع أو متطابق الضلعين أو متطابق الأضلاع زوايا المثلث الدرس (32) . قياس الزاوية الخارجية للمثلث يساوي مجموع قياسي الزاويتين الداخليتين البعيدتين المثلثات المتطابقة (الدرس 3-3 إلى 5-3 SSS يتطابق مثلثان إذا كانت أضلاعُهما المتناظرة متطابقة. • SAS يتطابق مثلثان إذا طابق ضلعان والزاوية المحصورة بينهما في المثلث الأول نظائرها في المثلث الآخر. . ASA يتطابق مثلثان إذا طابقت زاويتان والضلع المحصور بينهما في المثلث الأول نظائرها في المثلث الآخر. .AAS : يتطابق مثلثان إذا طابقت زاويتان وضلع غير محصور بينهما في المثلث الأول نظائرها في المثلث الآخر. المثلثات المتطابقة الضلعين والمثلثات المتطابقة الأضلاع (الدرس (3) المثلث المختلف الأضلاع (ص. (13) الضلع المحصور (ص. (45) المستقيم المساعد (ص 20) الزاوية الخارجية (ص. (22) الزاويتان الداخليتان البعيدتان (ص. (22) البرهان التسلسلي (ص. (22) اختبر مفرداتك ساقا المثلث المتطابق الضلعين (ص. 54) زاوية الرأس (ص 54) زاويتا القاعدة (ص. 54) البرهان الإحداثي (ص. (62) حدد ما إذا كانت كل عبارة فيما يأتي صحيحة أم خاطئة. وإذا كانت خاطئة فاستبدل ما تحته خط لتصبح صحيحة: (1) المثلث المتطابق الزوايا هو مثال على المثلث الحاد الزوايا. (2) المثلث الذي يحوي زاوية أكبر من 900 هو مثلث قائم الزاوية. زاويتا القاعدة في المثلث المتطابق الضلعين متطابقتان (3) المثلث المتطابق الأضلاع يكون متطابق الزوايا دائما. ويكون المثلث متطابق الأضلاع إذا تطابقت جميع زواياه. المثلثات والبرهان الإحداثي (الدرس (37) . يستعمل البرهان الإحداثي الأشكال في المستوى الإحداثي والجبر؛ لإثبات صحة المفاهيم الهندسية المطويات منظم أفكار تأكد من أن المفاهيم الأساسية مدونة في مطويتك. المثلثات المتطابقة (4) المثلث المختلف الأضلاع فيه ضلعان متطابقان على الأقل. (5) الضلع المحصور هو الضلع الذي يقع بين زاويتين متتاليتين في مضلع 6) البرهان التسلسلي يستعمل الأشكال في المستوى الإحداثي والجبر لبرهنة المفاهيم الهندسية. (7) قياس الزاوية الخارجية لمثلث يساوي مجموع قياسي الزاويتين الداخليتين البعيدتين. 68 الفصل 3 المثلثات المتطابقة وزارة التعليم Ministry of Education 2024-1446

حدد ما إذا كانت كل عبارة فيما يأتي صحيحة أم خاطئة. وإذا كانت خاطئة فاستبدل ما تحته خط لتصبح صحيحة المثلث المتطابق الزوايا هو مثال على المثلث الحاد الزوايا

مفاهيم اساسية
مراجعة الدروس 3-1 تصنيف المثلثات (ص: 12-18) صنف كلًا من المثلثات الآتية إلى حاد الزوايا أو متطابق الزوايا أو منفرج الزاوية أو قائم ال الزاوية B مثال 1 صنف كلا من المثلثين الآتيين إلى حاد الزوايا أو متطابق الزوايا أو منفرج الزاوية أو قائم الزاوية. 30° 110° 40° بما أن للمثلث زاوية منفرجة، فيكون مثلئًا منفرج الزاوية. 60° 60° (a (b 25/30° 35° 120°/60° A D C AADB 8 ABCD (9 AABC (10 جبر أوجد قيمة ، وأطوال الأضلاع المجهولة في المثلثات الآتية: 2x+7 (11 R T 3x-5 42 60° للمثلث ثلاث زوايا حادة جميعها متساوية؛ لذا فهو مثلث متطابق الزوايا. الفصل 3 دليل الدراسة والمراجعة الت69 Ministry of Edu 2024-1446 S K (12 12 3x+6 4x 5x-6 L 13) خرائط المسافة من الرياض إلى المدينة المنورة ومنها إلى مكة المكرمة ثم إلى الرياض تساوي km 2092، والمسافة بين الرياض ومكة المكرمة تزيد km 515 على المسافة بين المدينة المنورة ومكة المكرمة والمسافة بين المدينة المنورة ومكة المكرمة تقل km 491 عن المسافة بين الرياض والمدينة المنورة. أوجد المسافة بين كل مدينتين من هذه المدن وصنف المثلث الذي رؤوسه هذه المدن الثلاث.

مثال 1 صنف كل من المثلثات الأتية الى حاد الزاوية أو متطابق الزوايا او منفرج الزاوية أو قائم الزاوية
وزارة التعليم Ministry of Education 2024-1446 0 P P2 R 33° 51° 1 S عوض اطرح 51 من الطرفين نظرية مجموع قياسات زوايا المثلث عوض بسط اطرح 72 من الطرفين مثال 2 أوجد قياس كل من الزوايا المرقمة في الشكل المجاور: دليل الدراسة والمراجعة الفصل 3 3-2 زوايا المثلثات (ص 20-27 أوجد قياس كل من الزوايا المرقمة الآتية: 75° 2 28° 1 35° mz2+mZPQS = 90° 3 21 (14 22 (15) 23 (16 m22 + 51° = 90° m22 = 39° m21 + mZ2 + 33° = 180° m/139° 33° = 180° 17 منازل حديقة منزلية على صورة مثلث متطابق الضلعين كما في الشكل أدناه أوجد قيمة x . m21 + 72° = 180° m1 = 108° 38° المثلثات المتطابقة (ص: 28-35) 3-3 بين أن كل مضلعين مما يأتي متطابقان، وذلك بتحديد العناصر المتناظرة المتطابقة جميعها ، ثم اكتب عبارة التطابق مثال 3 بين أن المثلثين الآتيين متطابقان، وذلك بتحديد العناصر المتناظرة المتطابقة جميعها، ثم اكتب عبارة التطابق M Q N P R ZN=ZR, ZM = ZQ, ZMPN=ZQPR الزوايا الأضلاع MN = QR, MP = PNP = RP جميع العناصر المتناظرة في المثلثين متطابقة؛ لذا فإن AMNP = AQRP G E H D J (18) A F CH B X 40 K (19 78° 41° 61 61 78° Y 41° 40 Z 20 فسيفساء: يُظهر الشكل المجاور جزءا من تبليط فسيفسائي. سم 4 مثلثات تبدو متطابقة في الشكل. الفصل 3 المثلثات المتطابقة 70

أوجد قياس كل من الزوايا المرقمة في الشكل المجاور:
بين أن كل مضلعين مما يأتي متطابقان، وذلك بتحديد العناصر المتناظرة المتطابقة جميعها، ثم اكتب عبارة التطابق

بين أن المثلثين الآتيين متطابقان، وذلك بتحديد العناصر المتناظرة المتطابقة جميعها، ثم اكتب عبارة التطابق:
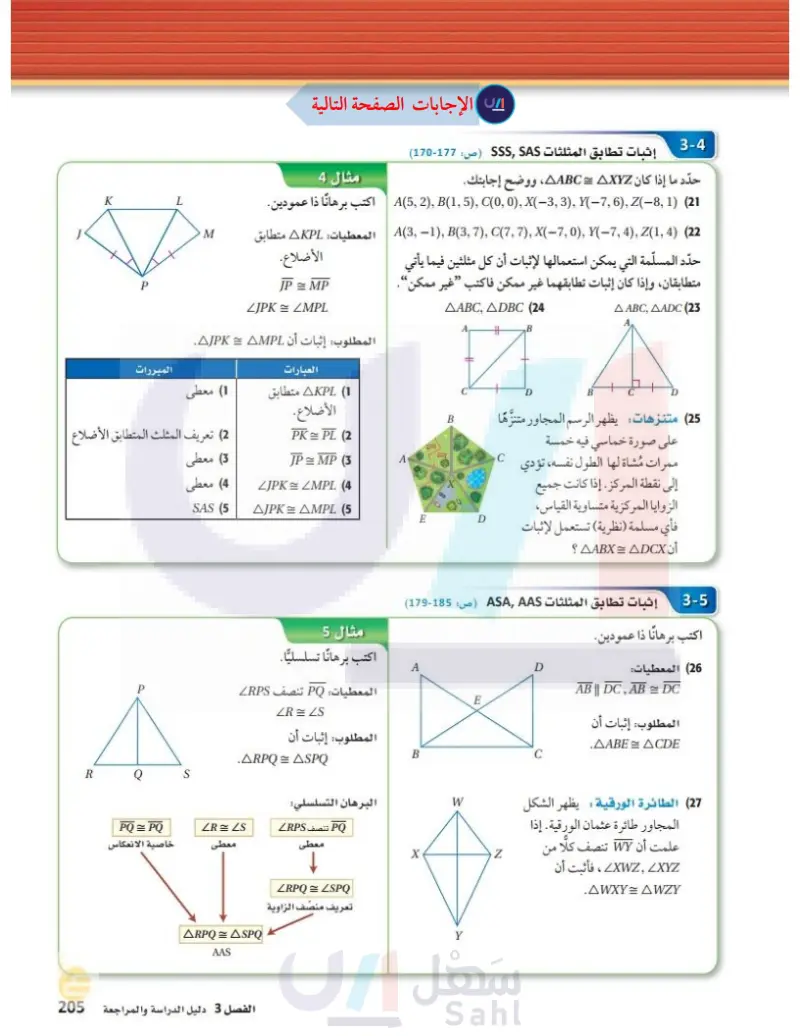
K L M مثال 4 اكتب برهانا ذا عمودين. AKPL: 3-4 إثبات تطابق المثلثات AS : - حدد ما إذا كان AABC = AXYZ، ووضح إجابتك. A(5, 2), B(1, 5), C(0, 0), X(-3, 3), Y(-7, 6), Z(-8, 1) (21 A(3,-1), B(3, 7), C(7, 7), X(-7, 0), Y(-7, 4), Z(1, 4) (22 حدد المسلّمة التي يمكن استعمالها لإثبات أن كل مثلثين فيما يأتي متطابقان، وإذا كان إثبات تطابقهما غير ممكن فاكتب غير ممكن. ABC, AADC (23) AABC, ADBC (24 # ,B D (25) متنزهات يظهر الرسم المجاور متنزها على صورة خماسي فيه خمسة ممرات مشاة لها الطول نفسه، تؤدي إلى نقطة المركز. إذا كانت جميع الزوايا المركزية متساوية القياس فأي مسلمة (نظرية) تستعمل لإثبات أن AABX = ADCX ؟ الأضلاع. JP = MP ZJPK = ZMPL المطلوب إثبات أن AJPK = AMPL. العبارات 1) AKPL متطابق الأضلاع. PK = PL (2) 1) معطى P المبررات (2) تعريف المثلث المتطابق الأضلاع (3) معطى (4) معطى JP = MP (3 ZJPKZMPL (4 A SAS (5 AJPK = AMPL P مثال 5 اكتب برهانا تسلسليا. المعطيات PQ تنصف RPS ZRZS المطلوب: إثبات أن .ARPQ=ASPQ R Q S PQ=PQ خاصية الانعكاس ZR = Z معطى ARPQ = ASPQ AAS الفصل 3 دليل الدراسة والمراجعة الت71 Ministry of Educe 2024-1446 البرهان التسلسلي PQ تنصف LRPS معطى ZRPQ = ZSPQ تعريف منصف الزاوية A B X 3-5 إثبات تطابق المثلثات SAAS (ص: 4-1) اكتب برهانا ذا عمودين. W Y E D C (26) المعطيات AB || DC, AB = DC المطلوب: إثبات أن .AABE = ACDE (27) الطائرة الورقية يظهر الشكل المجاور طائرة عثمان الورقية. إذا علمت أن WY تنصف كلا من XWZ XYZ ، فأثبت أن .AWXY=AWZY

حدد المسلمة التي يمكن استعمالها لإثبات أن كل مثلثين فيما يأتي متطابقان، وإذا كان إثبات تطابقهما غير ممكن فاكتب " غير ممكن "

مثال 4 اكتب برهانا ذا عمودين:
مثال 5 اكتب برهانا تسلسليا
B 12 44° A C الفصل 3 دليل الدراسة والمراجعة 3-6 المثلثات المتطابقة الضلعين والمثلثات المتطابقة الأضلاع (ص: 54-61) أوجد قيمة كل من المتغيرين فيما يأتي: مثال 6 أوجد كل قياس فيما يأتي: mZB (a BC ، وبتطبيق نظرية المثلث بما أن AB - BC ، فإن AB المتطابق الضلعين تكون زاويتا القاعدة AC متطابقتين؛ إذن mLA = mC. استعمل نظرية مجموع قياس زوايا المثلث لكتابة معادلة. ثم حلها لتجد mB. وزارة التعليم Ministry of Education 2024-1446 نظرية مجموع زوايا المثلث mZA = mLC = 44° بسط اطرح 88 من الطرفين mZA + mZB + mZC = 180 mZB + 44 + 44 = 180 m2B + 88 = 180 mZB = 92° AB (b AB = BC ؛ إذن AABC متطابق الضلعين. وبما أن 12 = BC ، فإن 12 = AB أيضًا. 52° (29 (28 12 12 10 3 x+4 15x - 1 -25° 7x-7 (30) رسم : يستعمل وليد حاملا خشبيا للرسم. والقطعة الداعمة الأفقية في الحامل تشكل . مثلئًا . متطابق الضلعين مع الدعامتين الأماميتين كما في الشكل المجاور، ما قياس كل من زاويتي قاعدة المثلث؟ 3-7 المثلثات والبرهان الإحداثي (ص: 62-67) 31) ارسم AMNO القائم الزاوية في ، طولا ضلعيه . (32) جغرافيا عين شاكر المدينة المنورة وبريدة وحائل كما هو مبين على الخريطة المجاورة. اكتب برهانا إحداثيا لإثبات أن المثلث الذي رؤوسه هذه المدن الثلاث مختلف الأضلاع. المدينة المنورة مثال 7 ارسم المثلث AABC المتطابق الضلعين والقائم الزاوية وطول كل من ساقي القائمة يساوي » وحدة على الربع الرابع في المستوى الإحداثي، وحدد إحداثيات رؤوسه. . اجعل نقطة الأصل رأسًا للزاوية • القائمة في المثلث. اجعل أحد ضلعي القائمة على المحور x ، والضلع الآخر على المحور ا. A(0, 0) 0 B(a, 0) I C(0,-a) . بما أن النقطة B على المحور x ، إذن إحداثيها لا يساوي صفرًا، وإحداثيها x يساوي .. وبما أن AABC متطابق الضلعين، فإن C ستبعد عن نقطة الأصل ه وحدة وإحداثيها (a - (0) ؛ لأنها تقع على الجزء السالب من المحور y ، وذلك لكي يكون المثلث في الربع الرابع. الفصل 3 المثلثات المتطابقة 72

أوجد كل قياس فيما يأتي
ارسم المثلث ABC المتطابق الضلعين والقائم الزاوية وطول كل من ساقي القائمة يساوي a وحدة على الربع الرابع في المستوى الإحداثي، وحدد إحداثيات رؤوسه
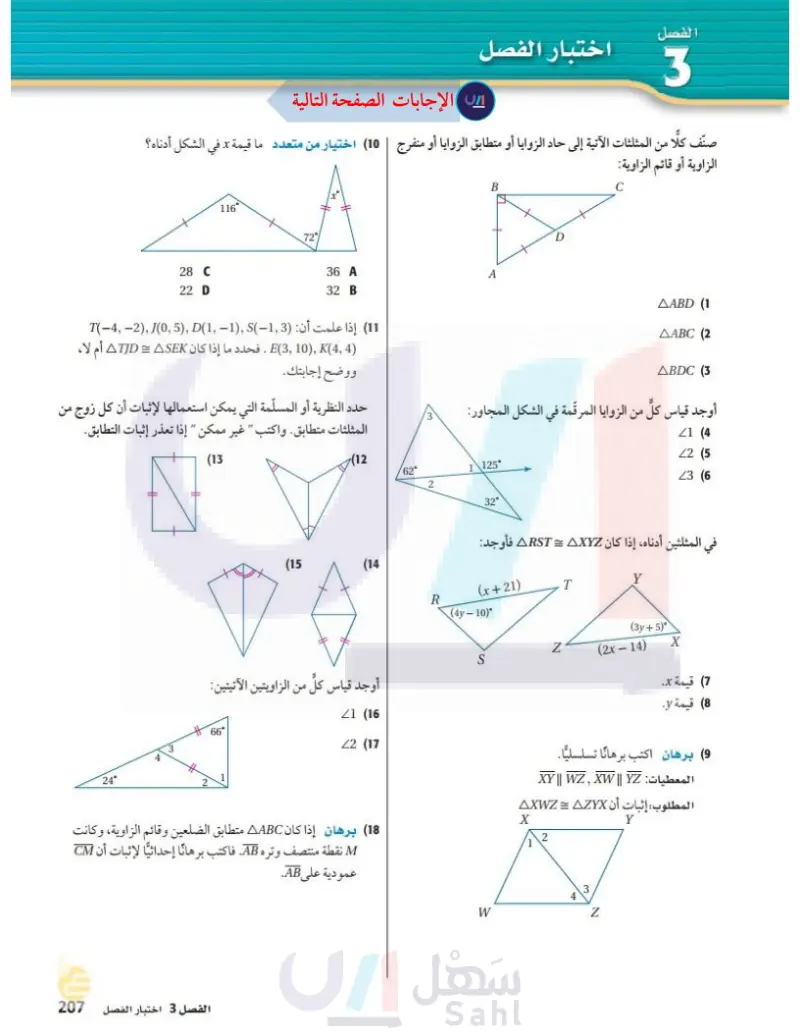
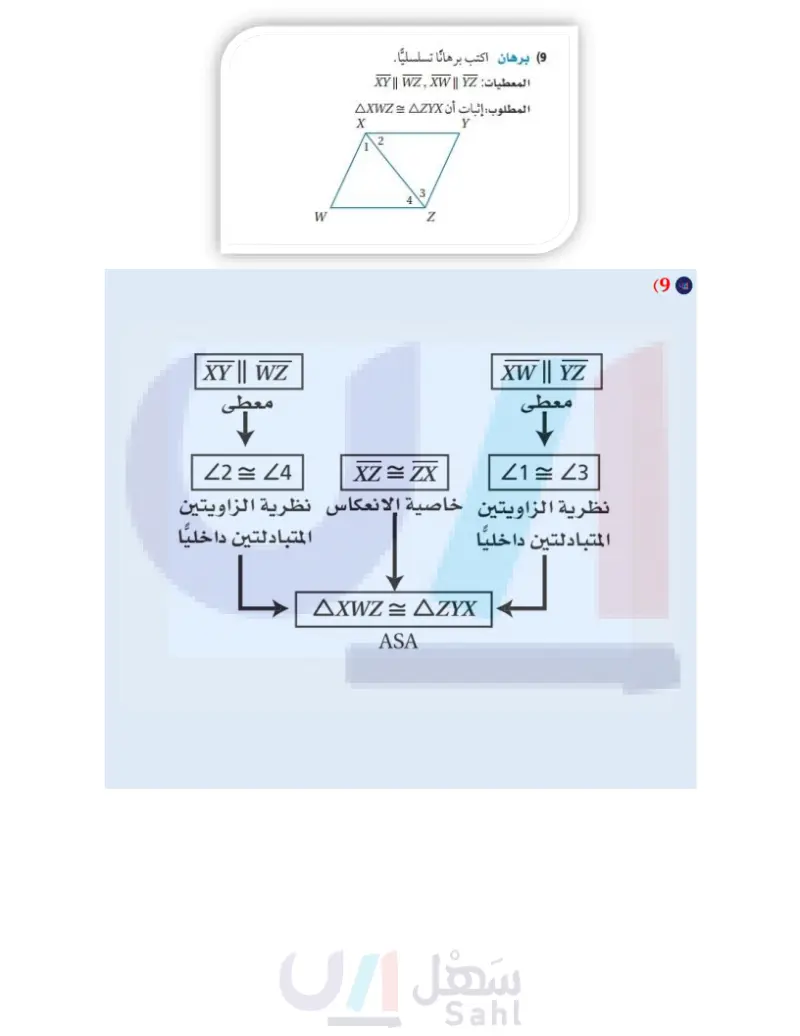
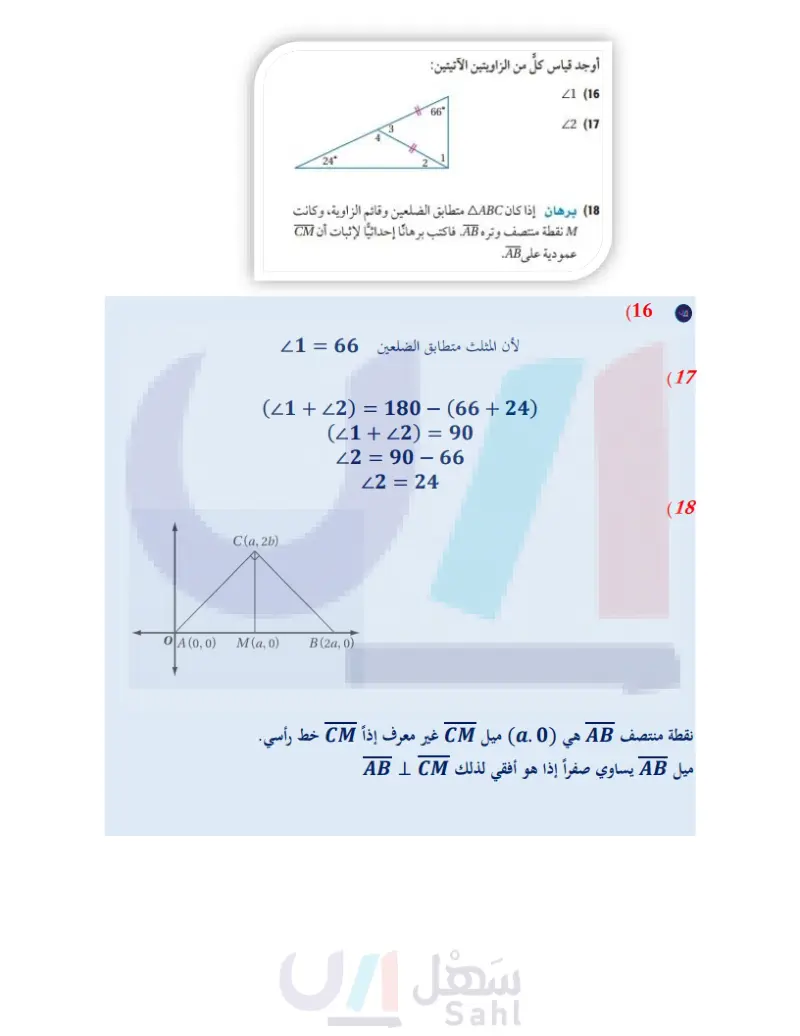
الفصل 3 اختبار الفصل صنف كلا من المثلثات الآتية إلى حاد الزوايا أو متطابق الزوايا أو منفرج | 10 اختيار من متعدد ما قيمة تد في الشكل أدناه؟ 28 C 22 D 116° T(-4,-2), J(0,5), D(1, -1), S(-1, 3) : 36 A 32 B A (11 (4 ,4) (3) . فحدد ما إذا كان ATID = ASEK أم لا، ووضح إجابتك. حدد النظرية أو المسلّمة التي يمكن استعمالها لإثبات أن كل زوج من المثلثات متطابق. واكتب " غير ممكن " إذا تعذر إثبات التطابق. 24° (13 (15 B D الزاوية أو قائم الزاوية: C ABD (1 AABC (2 ABDC (3 أوجد قياس كل من الزوايا المرقمة في الشكل المجاور: (12 62° 1 125° 2 (14 أوجد قياس كل من الزاويتين الآتيتين: 66° 21 (16 22 (17 (18) برهان إذا كان AABC متطابق الضلعين وقائم الزاوية، وكانت M نقطة منتصف وتره .AB. فاكتب برهانًا إحداثيا لإثبات أن CM الفصل 3 اختبار الفصل الـ 73 Ministry of E 2024-1446 عمودية على AB. 32° 21 (4) 22 (5) Z3 (6 في المثلثين أدناه ، إذا كان ARST = AXYZ فأوجد: (x+21) T Y R (4y-10) (3y+5) Z (2x-14) X S W (7) قيمة . (8) قيمة . 9) برهان اكتب برهانا تسلسليا. المعطيات XY || WZ, XW || YZ المطلوب: إثبات أن AXWZ = AZYX X 2 3 Z Y

لفصل الإعداد للاختبارات 3 الأسئلة ذات الإجابات القصيرة الأسئلة ذات الإجابات القصيرة تتطلب منك أن تقدم حلًا لها متضمنا الطريقة والتبريرات والتفسيرات التي استعملتها. و في العادة يتم تصحيحه هذه الأسئلة، وتحدد درجاتها باستعمال سلالم التقدير. وهذا مثال على تصحيح هذا النوع من الأسئلة. سلالم التقدير المعايير درجة كاملة الإجابة صحيحة مدعمة بتفسيرات كاملة توضح كل خطوة. درجة جزئية . الإجابة صحيحة، لكن التفسيرات ليست كاملة. • الإجابة غير صحيحة، لكن التفسيرات صحيحة. لا يستحق درجة لم يقدم أي إجابة، أو أن الإجابة ليس لها معنى استراتيجيات حل الأسئلة ذات الإجابات القصيرة | الخطوة 1 اقرأ السؤال جيدا؛ كي تفهم الشيء الذي تحاول حله. . حدد الحقائق ذات العلاقة. . ابحث عن الكلمات المفتاحية والمصطلحات الرياضية. الخطوة 2 ضع خطة وحل المسألة. . فسر تبريرك، أو اعرض الطريقة التي ستتبعها لحل المسألة. 74 . اكتب الحل كاملا مبينا الخطوات جميعها. . تحقق من إجابتك إذا سمح الوقت بذلك. مثال الدرجة 2 1 1 0 اقرأ السؤال الآتي، وحدد المطلوب. ثم استعمل المعلومات الواردة في السؤال لحله. واكتب خطوات الحل. ما محيط المثلث ABC متطابق الضلعين الذي قاعدته BC؟ الفصل 3 المثلثات المتطابقة 2x+4 A 3x - 1 A B 4(x-2) C وزارة التعليم Ministry of Education 2024-1446

الاسئلة ذات الاجابات القصيرة
اقرأ السؤال الآتي، وحدد المطلوب
اقرأ السؤال بعناية. تَعْلَم من السؤال أن AABC متطابق الضلعين قاعدته BC، والمطلوب أن تجد محيط هذا المثلث. ضع خطة وحل السؤال. ضلعا المثلث المتطابق الضلعين متطابقان. لذا B = AC أو AB = AC . والآن حل المعادلة لتجد قيمة x . AB = AC 2x+4=3x-1 2x - 3x = -1 -4 -x = -5 x = 5 ثم أوجد طول كل ضلع من أضلاع المثلث. 2(5) + 4 = 14 : AB 3(5) - 1 = 14 :AC 4(52) 12 BC وبما أن 40 = 12 + +14+ 14 ، إذن محيط AABC يساوي 40 وحدة. خطوات الحل والحسابات والتبريرات واضحة. وتوصل الطالب إلى الإجابة الصحيحة؛ إذن تستحق هذه الإجابة درجتين. | تمارين ومسائل اقرأ كل سؤال فيما يأتي، وحدد المطلوب، ثم استعمل المعلومات (3) يحتاج مزارع إلى إنشاء حظيرة مستطيلة الشكل لأغنامه، مساحتها 2 m 1000 ، ويريد أن يوفر المال عن طريق شراء أقل كمية ممكنة الواردة في السؤال واكتب خطوات الحل (1) صنف ADEF بحسب زواياه. من السياج. إذا كانت أبعاد الحظيرة أعدادًا صحيحة، فأوجد بعدي القطعة التي تتطلب أقل كمية من السياج. (4) في الشكل أدناه ARST = AVUT . ما مساحة ARST؟ R V 15x S 11x - 2 T 8x + 4 u الفصل 3 الإعداد للاختبارات الت75م Ministry of E 2024-1446 E (2x + 11) (4x+7)° (7x-3)° D F 2) اكتب معادلة المستقيم المار بالنقطتين: (02) (2) .

اختبار تراكمي للفصول 3-1 لفصل 3 أسئلة الاختيار من متعدد اختر رمز الإجابة الصحيحة فيما يأتي: 1) يصنف المثلث المرسوم أدناه بحسب أضلاعه بأنه: 32m 40 m ما قياس الزاوية R في الشكل أ أدناه؟ R A 125% T 68° S 57° A 24 m A متطابق الأضلاع B متطابق الضلعين قائم الزاوية مختلف الأضلاع (2) في المثلثين أدناه إذا كان : WX = JK, YX = IK, EK K W 59° B 65° C 68° D (4) افترض أن قياس إحدى زاويتي القاعدة في مثلث متطابق الضلعين يساوي 44، فما قياس زاوية رأس المثلث؟ وزارة التعليم Ministry of Education 2024-1446 32° 70° 108° A 92° B X 56° C 44° D (5) أوجد m1؟ 85° A 63° B 47° C 32° D فأيُّ العبارات الآتية تعبر عن تطابق هذين المثلثين؟ AWXYAKIJ A AWXY = AIK B AWXY AJKI C AWXYAIJK D الفصل 3 المثلثات المتطابقة 76 16

أسئلة ذات إجابات قصيرة أجب عن كل مما يأتي: 6) إذا كان ANDG = ALGD في الشكل أدناه، فما قيمة x؟ N D 36° L G (7) في الشكل أدناه 22 = 1 ,IT I AP P T نے A حدد نظرية التطابق التي تبين أن [APTJ = AAT باستعمال المعطيات الواردة في السؤال فقط، ووضح إجابتك. (9) أثبت الجملة يتطابق مثلثان إذا تطابق ضلعان وزاوية غير محصورة بينهما من المثلث الأول مع نظائرها من المثلث الثاني" إذا كانت صحيحة بكتابة برهان حرّ، أو ارسم شكلا يبين عدم صحتِها. 10) إذا علمت أن AEFG = ADCB، فاكتب الزوايا والأضلاع المتناظرة في المثلثين. أسئلة ذات إجابات مطولة (11) أجب عن الأسئلة ad؛ لتحصل على برهان إحداثي للعبارة الآتية: المثلث الذي رؤوسه (40) (2) (0) هو مثلث متطابق الضلعين. عين الرؤوس على ورقة رسم بيانية 8) أوجد mLTUV في الشكل أدناه. V T 74° U هل تحتاج إلى مساعدة إضافية؟ إذا لم تستطع الإجابة عن .... فعد إلى الدرس... استعمل قانون المسافة لكتابة عبارة تمثل AB. استعمل قانون المسافة لكتابة عبارة تمثل BC. استعمل النتائج التي توصلت إليها في الفرعين ,b ؛ لتدون اسستنتاجك عن AABC. 11 10 9 8 7 6 5 4 3 2 1 3-7 3-3 3-4 3-6 3-5 3-3 3-2 3-6 3-2 3-3 3-1 الفصل 3 اختبار تراكمي الت77م Ministry of Edu 2024-1446




 0
0 

 0
0 

 0
0 
 0
0