رسم المنحنيات - التفاضل والتكامل - ثالث ثانوي
الوحدة الأولى: الاشتقاق وتطبيقاته
الوحدة الثانية: تفاضل وتكامل الدوال الأسية واللوغاريتمية
الوحدة الثالثة: سلوك الدالة ورسم المنحنيات
الوحدة الرابعة: التكامل المحدد وتطبيقاته
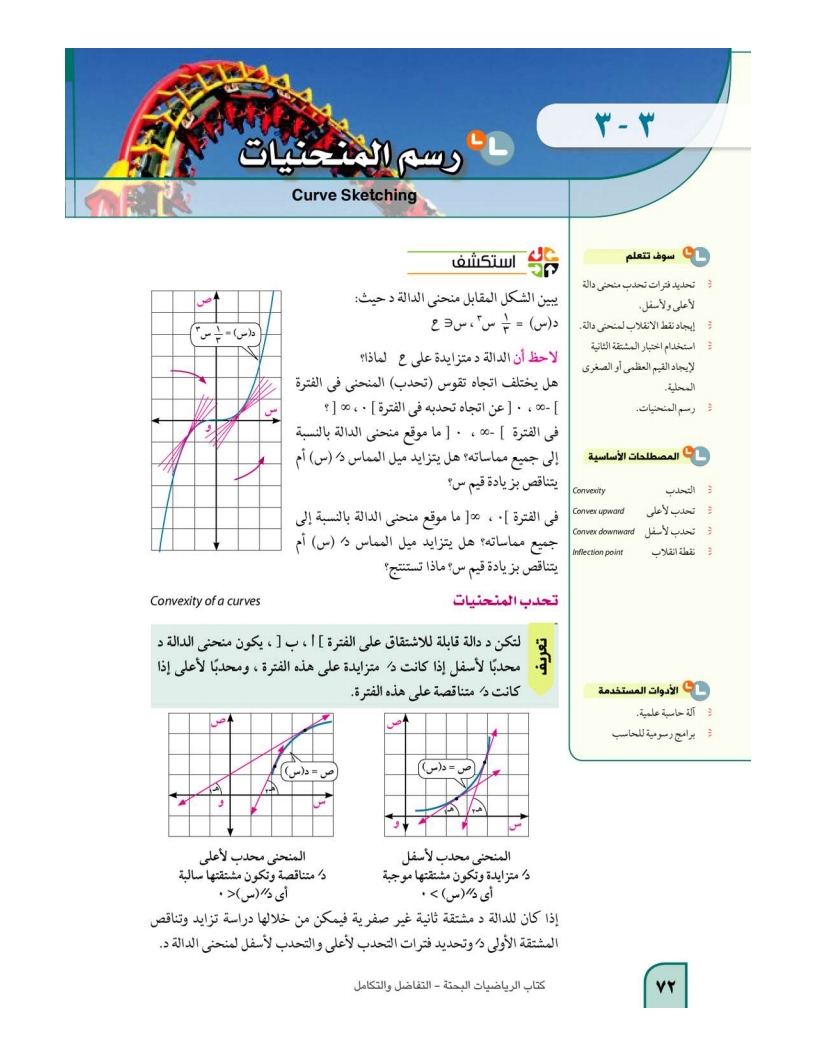
استكشف
تحدب المنحنيات
سوف تتعلم
المصطلحات الأساسية
الأدوات المستخدمة
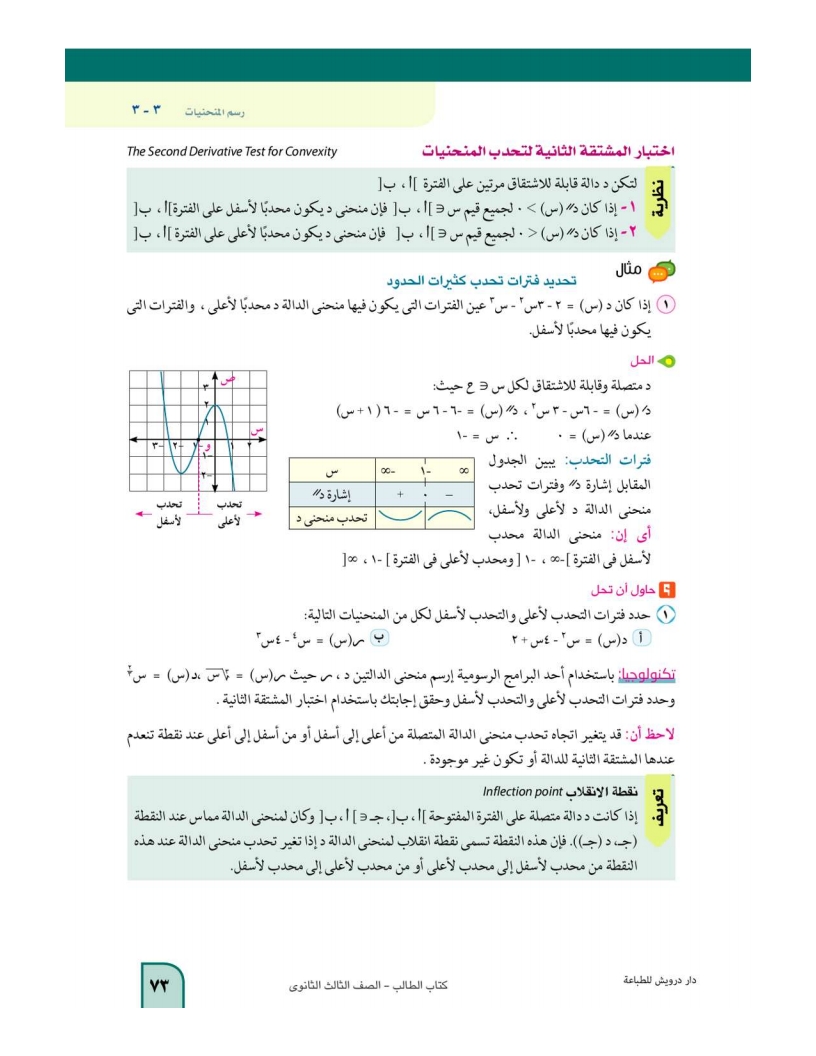
اختبار المشتقة الثانية لتحدب المنحنيات
مثال1: تحديد فترات تحدب كثيرات الحدود
تعريف نقطة الانقلاب
حاول أن تحل1: حدد فترات التحدب لأسفل لكل من المنحنيات التالية
تكنولوجيا: باستخدام أحد البرامج الرسومية إرسم منحنى الدالتين د
لاحظ أن: قد يتغير اتجاه تحدب منحنى الدالة المتصلة من أعلى إلى أسفل أو من أسفل إلى أعلى
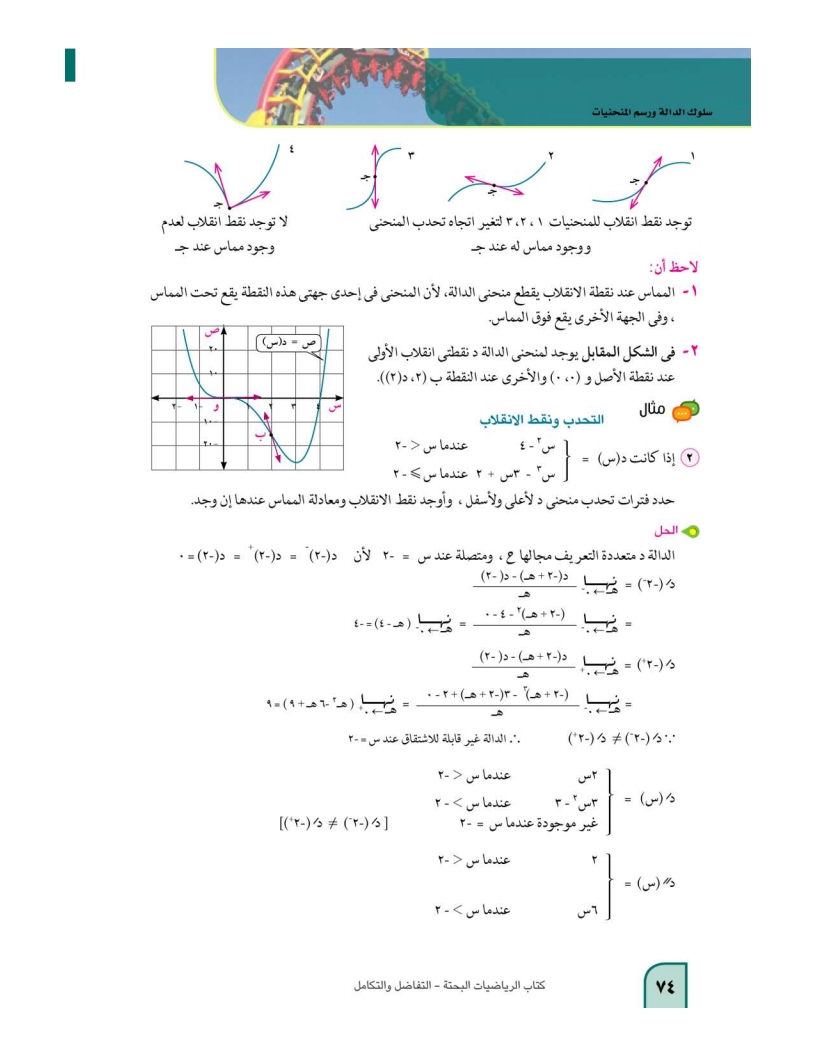
تابع النظرية
مثال2: التحدب ونقط الانقلاب
تابع مثال2: التحدب ونقط الانقلاب
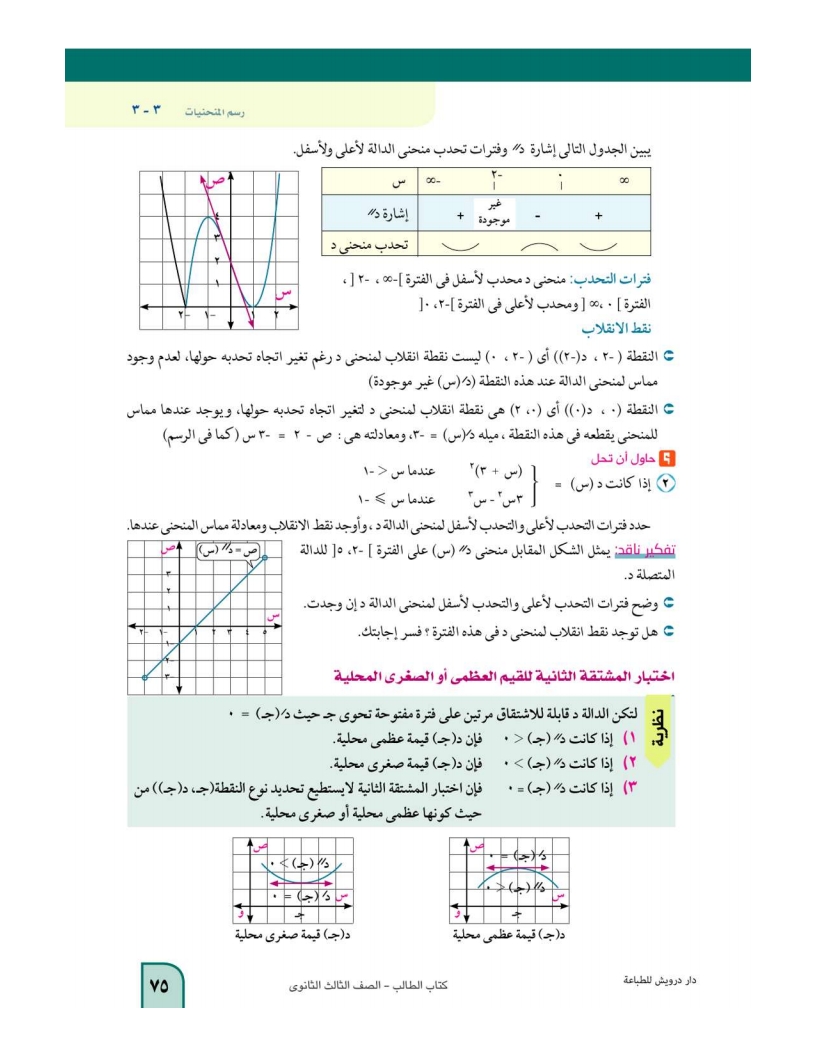
اختبار المشتقة الثانية للقيم العظمى أو الصغرى المحلية
حاول أن تحل2: حدد فترات التحدب لأعلى والتحدب لأسفل لمنحنى الدالة د
تفكير ناقد: وضح فترات التحدب لأعلى والتحدب لأسفل لمنحنى الدالة د إن وجدت

مثال3: استخدم اختيار المشتقة الثانية في إيجاد القيم العظمى والصغرى المحلية للدالة د حيث
رسم الشكل العام لمنحنبات كثيرات الحدود
حاول أن تحل3: باستخدام اختبار المشتقة الثانية أوجد القيم العظمى والصغرى المحلية للدالة د

مثال4: رسم منحنى دالة
حاول أن تحل4: ارسم الشكل العام لمنحنى الدالة د حيث ص
مثال5: الشكل العام لمنحنى دالة
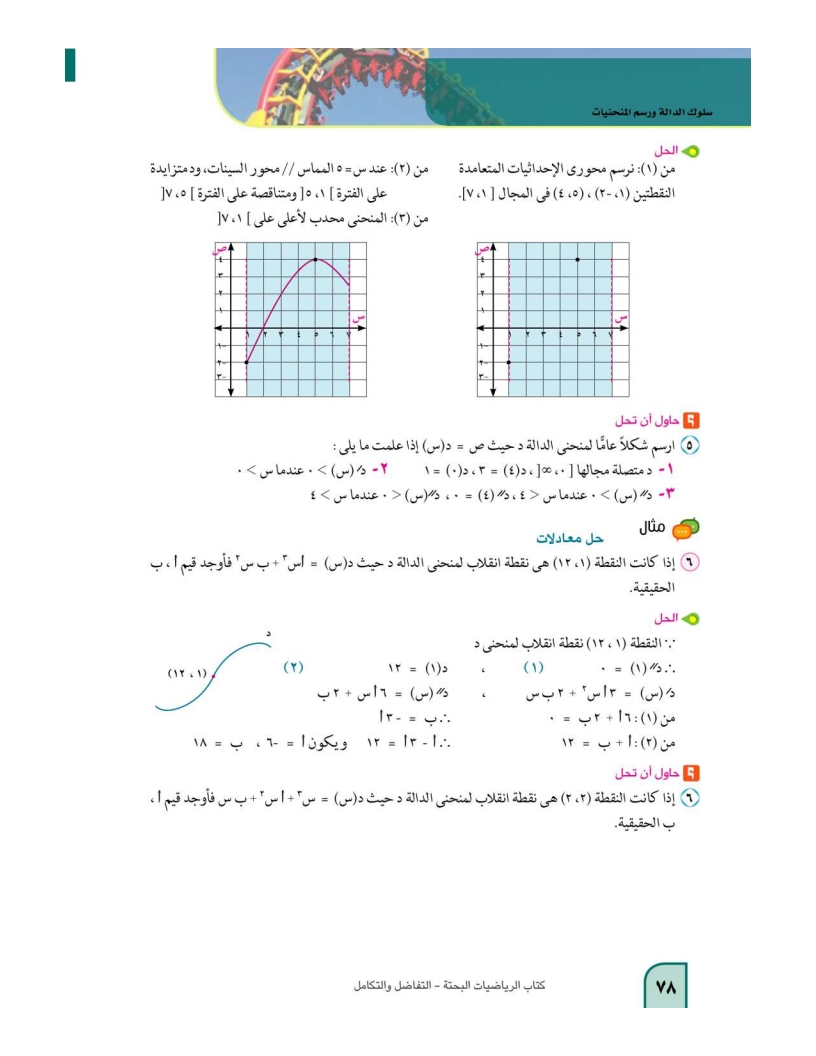
تابع مثال5: الشكل العام لمنحنى دالة
مثال6: حل معادلات
حاول أن تحل5: ارسم شكلا عاما لمنحنى الدالة د حيث ص
حاول أن تحل6: فأوجد قيم أ , ب الحقيقية

نشاط استخدام الحاسبة البيانية في رسم الدوال
يوضح الشكل المقابل منحنى الدالة ص79

تمارين 3-3: يبين الشكل المقابل منحنى الدالة د حيث ص = د(س)
ابحث فترات تحدب الدالة د ثم أوجد إحداثيات نقط الانقلاب (إن وجدت)لكل مما يأتي
ارسم الشكل العام لمنحنى الدالة المتصلة د الذي له الخواص المعطاة في كل مما يأتي
تمرين10: أثبت أن قياس زاوية ميل المماس عند نقطة الانقلاب لمنحنى الدالة د حيث
تمرين11: إذا كان لمنحنى الدالة د حيث
تمرين13: أوجد أ , ب بحيث يكون للمنحنى

ادرس تغيرات الدالة د وارسم الشكل العام لمنحناها في كل مما يأتي






