متوسطات المثلث - رياضيات 1 - ثاني اعدادي
الوحدة الأولى: الأعداد الحقيقية
الوحدة الثانية: العلاقة بين متغيرين
الوحدة الثالثة: الإحصاء
الوحدة الرابعة: متوسطات المثلث والمثلث المتساوي الساقين
الوحدة الخامسة: التباين
كتاب النشاط
الأنشطة والتدريبات
الوحدة الأولى: الأعداد الحقيقية
الوحدة الثانية: العلاقة بين متغيرين
الوحدة الثالثة: الإحصاء
الوحدة الرابعة: متوسطات المثلث والمثلث المتساوي الساقين
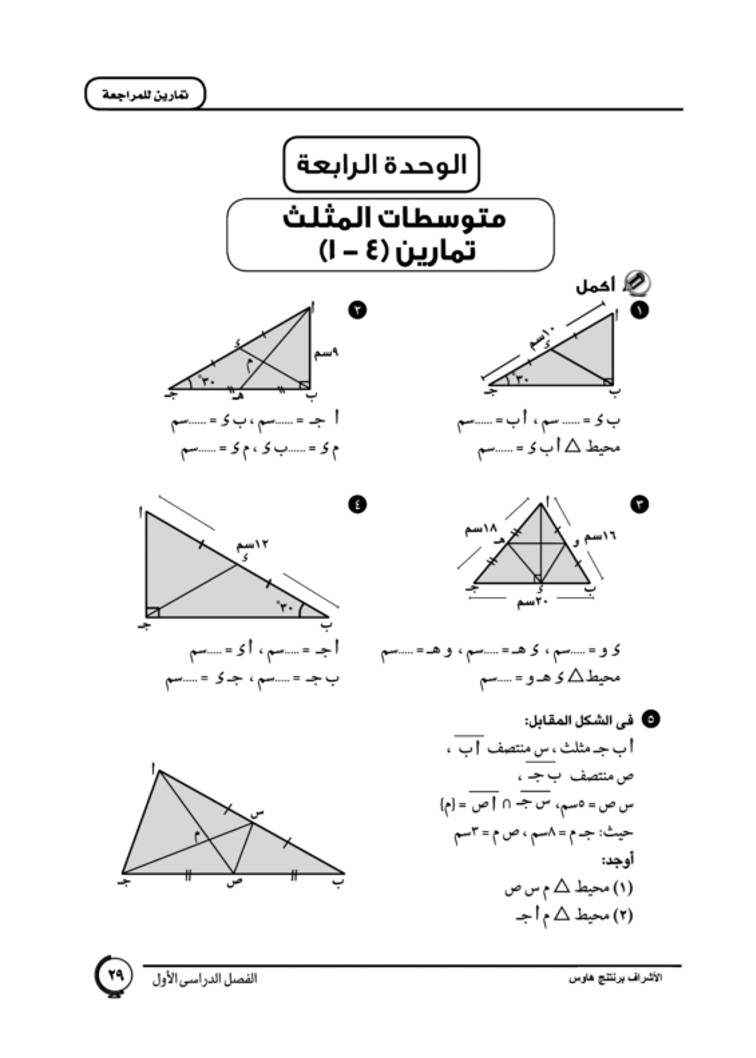
في الشكل المقابل : اب جـ مثلث ، س منتصف أ ب ، ص منتصف ب ج ، س ص = 5 سم ، س ج تقاطع أ ص =( م ) حيث : جـ م = 8 سم ، ص م = 3 سم أوجد : محیط المثلث م س ص محيط المثلث م ا ج
أكمل
أ ب جـ مثلث ، د منتصف ب ح ، م تنتمي ل أ د بحيث أ م =2 م د ، رسم ج م فقطع أ ب في هـ . فإذا كان هـ جـ = ١٢ سم أوجد طول هـ م
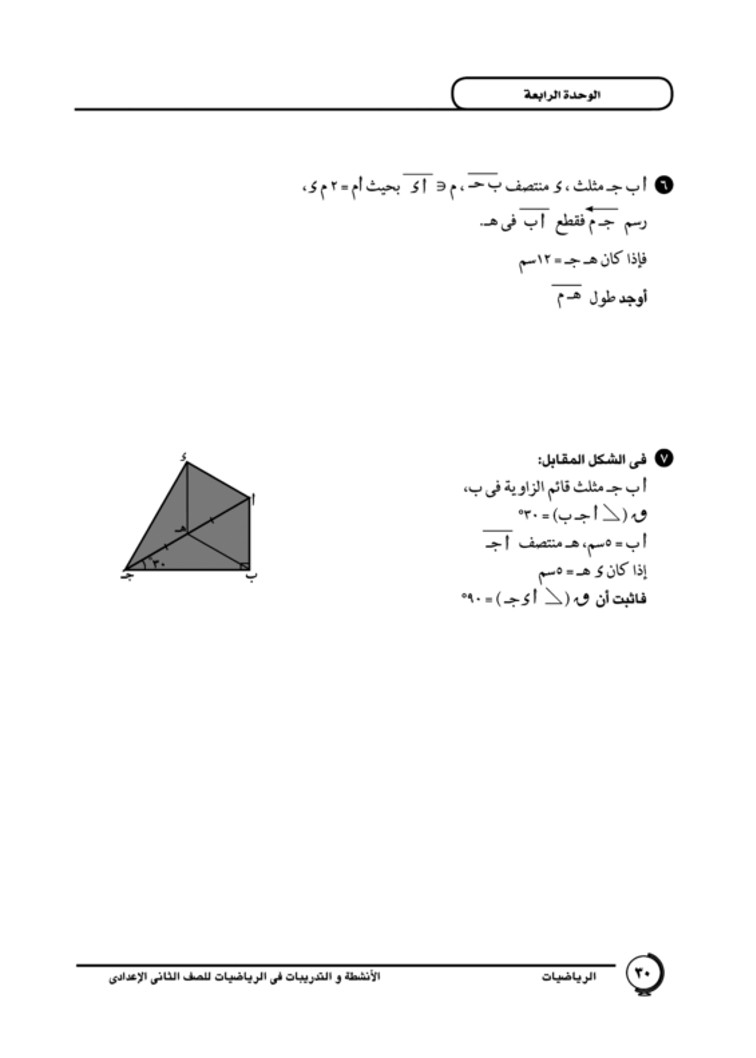
في الشكل المقابل : آب ج مثلث قائم الزاوية في ب . قياس ( ا ج ب ) =30 أ ب = 5 سم ، هـ منتصف ا ج إذا كان د ه = 5 سم فأثبت أن ق ( أ د ج ) = 9






