الضوء - فيزياء - ثاني ثانوي
الوحدة الأولى: الموجات
الوحدة الثانية: الموائع
الوحدة الأولى الموجات الفصل الثاني الفصل الثاني مقدمة الضوء جزء من مدى واسع من الموجات تسمى الموجات الكهرومغناطيسية تنتشر جميعها بسرعة ثابتة في الفراغ قدرها x 10 m/s 3 ، وتتباين فيما بينها في ترددها معطيه ما يسمى الطيف الكهرومغناطيسي (-) JK Electromagnetic Spectrum ويشمل على سبيل المثال موجات الراديو Radio Waves ، وموجات الأشعة تحت الحمراء Infrared وموجات الضوء المنظور Visible Light ، وموجات الأشعة فوق البنفسجية Ultraviolet ، وموجات الأشعة السينية X-rays ، وموجات أشعة جاما Gammar) -rays وجميعها لها خواص مشتركة. الضوء أشعة جاما أشعة إكس المدني تحت الحمراء موجات الراديو Micro- Radio Waves Infrared Waves X-rays Gamma rays 10% 104 1612 10 100 102 Hz فوق البنفسجية الموجات الدقيقة شكل (۲ - ۱) الطيف الكهرومغناطيسي 인 10 10 ويبين الرابط المقابل الخواص المشتركة للموجات الكهرومغناطيسية فهي تنتشر أو تنتقل في الفضاء بنفس السرعة،وجميعها موجات مستعرضة. وإن كانت تختلف في تردداتها وأطوالها الموجية مطابع زمزم ۲۳ الفيزياء الصف الثانى الثانوى |
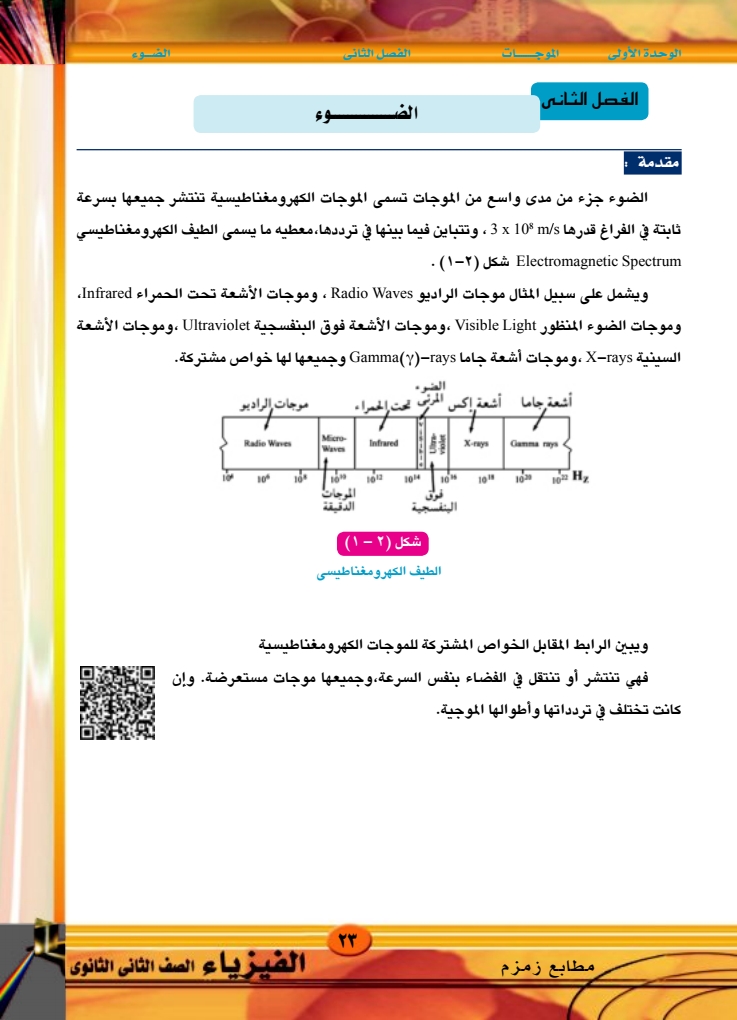
مقدمة
الوحدة الأولى الموجات الفصل الثاني الضو انعكاس الضوء وانكساره ينتشر الضوء في جميع الإتجاهات في خطوط مستقيمة ما لم يصادفه وسط عائق. فإذا صادفه عائق فإنه يعاني انعكاساً أو انكساراً أو إمتصاصاً بنسب مختلفة حسب طبيعة الوسط العائق. عند سقوط شعاع ضوئي على سطح فاصل بين وسطين مختلفين في الكثافة الضوئية فإن جزءاً من الضوء ينعكس، والجزء الآخر ينكسر مع إهمال الجزء الممتص. ونلاحظ من الشكل المقابل ما يلي: يقع كل من الشعاع الساقط والمنعكس والمنكسر والعمود المقام على السطح الفاصل من نقطة السقوط في مستوى واحد عمودي على السطح الفاصل. الشعاع المنعكس الوسط الأول (هواء) الوسط الثاني (زجاج) الشعاع الساقط . في حالة الإنعكاس: زاوية السقوط = زاوية الانعكاس . في حالة الإنكسار : النسبة بين جيب زاوية السقوط في الوسط الأول إلى جيب زاوية الإنكسار في الوسط الثانى كالنسبة بين سرعة الضوء في الوسط الأول إلى سرعة الضوء في الوسط الثاني ، الشعاع المنكس زاوية و الانكسار شكل ( ۲ - ۲) انعكاس وانكسار الضوء وهي نسبة ثابتة لهذين الوسطين ويطلق عليها اسم معامل الإنكسار النسبي من الوسط الأول إلى الوسط الثاني . ويرمز له بالرمز 1 أي أن sin o sin e =n (2-1) 12 V2 نتائج هامة (۱) تعد سرعة الضوء في الفضاء أو الفراغ من الثوابت الكونية وتساوى m/s 10 × 3 ، وسرعة الضوء في الفضاء أو الفراغ أكبر من سرعته في أي وسط مادى. وإذا رمزنا لسرعة الضوء في الفراغ C V بالرمز c ولسرعة الضوء في الوسط المادي بالرمز 7 فإن النسبة تسمى معامل الانكسار المطلق لهذا الوسط ويرمز له بالرمز n وقيمته أكبر من الواحد الصحيح؟ الفيزياء الصف الثانى الثانوى n (2-2) v ٢٤ ۲۰۲۰ - ۲۰۱۹

انعكاس الضوء وانكساره
نتائج هامة
الوحدة الأولى الموجات الفصل الثاني ومعاملات انكسار بعض المواد مدرجة في الجدول التالي: معامل الانكسار له n الوسط المادي واء 11 ــاء ـزيـ ــن رابع كلوريد الكربون الكحـ الزج ول الإيثيلي اج التـ الزجاج الصـ ـرى اجی المـ ساس (۲) من العلاقة (2-2) يتضح أن: أي أن ومنها يكون وبالتعويض من (3-2) في (1-2) أي أن n (2-3) v= = sin p sin 0 2 = 1.00293 1.333000 1.501000 1.461000 1.361000 1.52000 1.660000 1.4850000 2.419000 ny sin Q = n, sin 0 (2-4) وهذا ما يعرف بقانون سنل Snell's law أي أن حاصل ضرب معامل الانكسار المطلق لوسط السقوط في جيب زاوية السقوط يساوي حاصل ضرب معامل الانكسار المطلق لوسط الانكسار في جيب زاوية الانكسار. مطابع زمزم ۲۵ الفيزياء الصف الثانى الثانوى |

معاملات انكسار بعض المواد
الوحدة الأولى الموجات الفصل الأول الضوء - يمكن استخدام الانكسار في تحليل حزمة ضوئية إلى مركباتها ذات الأطوال الموجية المختلفة حيث يختلف معامل الانكسار المطلق تبعاً للطول الموجي، ولذلك يتشتت الضوء الأبيض إلى مكوناته، ويمكن ملاحظة ذلك في فقاعات الصابون. معلومة إثرائية تفسير الانكسار إذا سقط الضوء من وسط أقل كثافة إلى وسط أعلى كثافة اقترب الشعاع المنكسر من العمود ويماثل ذلك عربة تدخل إحدى عجلاتها في منطقة طينية تبطئها، بينما العجلة الأخري أسرع، فيحدث انحناء في المسار (شكل ۲-۳). والعكس حين يحدث انكسار من المنطقة أعلي في الكثافة إلى منطقة أقل فى الكثافة فيكون الشعاع المنكسر بعيدا عن العمود (شكل ٢-٤) طريق مرصوف HHHHH اقناع منكر تربة طينية زجاج قرية طينية شعاع ساقط HHH طريق مرصوف شكل ( ۲ - ۳) إنكسار من وسط أقل كثافة إلى وسط اكبر كثافة شكل (٢ - ٤ ) . إنكسار من وسط اكبر كثافة إلى وسط القل كثافة الفيزياء الصف الثانى الثانوى ٢٦ ۲۰۲۰ - ۲۰۱۹
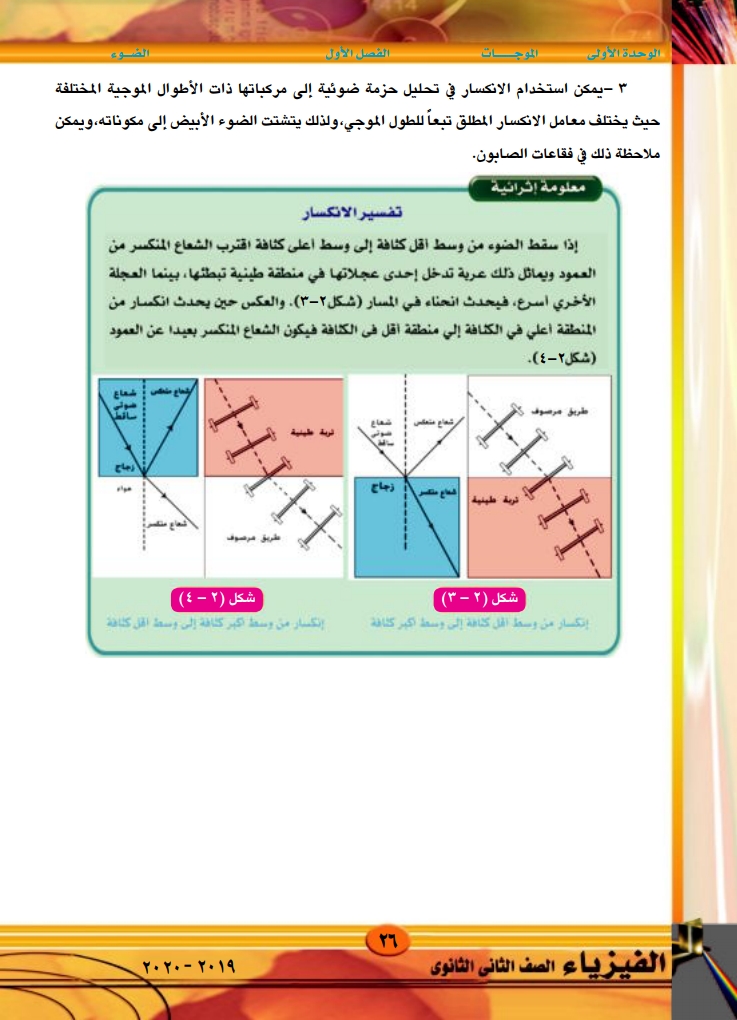
معلومة إثرائية
3/ يمكن استخدام الانكسار في التحليل
الوحدة الأولى الموجات الفصل الثاني أمثلة 1- إذا سقط شعاع ضوئى على سطح لوح زجاجي معامل انكساره 1.5 بزاوية سقوط °30 فاحسب زاوية الإنكسار. الحل ومنها ... n= sin sing xin 30 1.5 = sine 0.5 sing = 0.333 1.5 .. 6 = 19 28 - إذا كان معامل الانكسار المطلق للماء. ومعامل الإنكسار المطلق للزجاج 3 فأوجد: 3 أ- معامل الانكسار النسبي من الماء إلى الزجاج. 2 بمعامل الانكسار النسبى من الزجاج إلى الماء. الحل: أ- معامل الانكسار النسبى من الماء إلى الزجاج 3 , 2 9 = 0] 8 ب-معامل الانكسار النسبي من الزجاج إلى الماء. 4 n 211= = 11 9 ومن هذا المثال نتبين أن 1 ال ، وهي نتيجة هامة. مطابع زمزم Д ۲۷ الفيزياء الصف الثانى الثانوى |

2/ فاحسب زواية الانكسار
2/ فأوجد معامل الانكسار النسبي من الماء الى الزجاج
الوحدة الأولى الموجات الفصل الأول الضوء تداخل الضوء Light Interference : أجرى توماس ينج Young تجربة لدراسة ظاهرة التداخل في الضوء فيما يعرف باسم تجربة الشق المزدوج Double Slit Experiment وهي موضحة بالشكل (٢-٥). في هذا الشكل مصدر ضوئي أحادى اللون Monochromatic Source اى أن للطول الموجي ة قيمة واحدة ثابتة، يقع على بعد مناسب من حاجز به فتحة مستطيلة ضيقة ؟ تمر خلالها موجات أسطوانية نحو حاجز به فتحتان مستطيلتان ضيقتان SS ، تعملان کشق شكل ( ٢ - ١٥) نهاية عظمي ابقه البطين) ات العلياء نهاية عظمي الله البطين) نهاية صفري شكل ٢) - (٥) ب) ظاهرة التداخل في رسم تخطيطي لتجربة تجربة يونج يونج مزدوج. تقع على نفس صدر الموجة الأسطوانية. لذلك يكون للموجات التي تصلها نفس الطور. وتسلك الفتحتان المستطيلتان سلوك المصادر المترابطة ، وهي تلك المصادر التي تكون موجاتها متساوية التردد والسعة ولها نفس الطور. وعلى الحائل C تتراكب موجات الحركتين الموجيتين القادمتين إليه من S ، S، ونتيجة لهذا التراكب تظهر مجموعة التداخل التي تبدو كمجموعة من المناطق المستقيمة المتوازية ، وهي عبارة عن مناطق مضيئة تتخللها أخرى مظلمة تعرف باسم هدب التداخل nterference Fringes ، ، كما في الشكل (٢-٦). والمسافة بين أي هدبتين متتاليتين Ay من نفس النوع تتعين من العلاقة AR Ay = (2-5) d حيث طول موجة الضوء الأحادي اللون المستخدم، R المسافة بين الشق شكل (٢ - ٦) المزدوج والحائل المعد لاستقبال الهدب و d المسافة بين S . لذلك تستخدم هذه التجربة لتعيين الطول الموجى لأى ضوء أحادي اللون. هدب التداخل الفيزياء الصف الثانى الثانوى ۲۸ ۲۰۲۰ - ۲۰۱۹

تداخل الضوء
الوحدة الأولى الموجات الفصل الثاني مثال: 1- في تجربة الشق المزدوج كانت المسافة بين الفتحتين المستطيلتين الضيقتين m 0.00015 وكانت المسافة بين الشق والحائل المعد لاستقبال الهدب 0.75m وكانت المسافة بين هدبتين مضيئتين هي m 0.003 احسب الطول الموجى للضوء الأحادي اللون المستخدم. الحل AR Ay = d 0.75 x 0.003- 0.00015 0.00015 x 0.003 =λ = 0.6 x 106 m 0.75 2 = 100 x 0.6 x 106 = 6000 حيود الضوء : Light Diffraction عندما يسقط ضوء أحادى اللون على فتحة دائرية فى حاجز، فإننا نتوقع تبعًا لمعلوماتنا عن انتشار الضوء في خطوط مستقيمة أن تتكون على الحائل الموضح في الشكل بقعة دائرية مضيئة محددة. لكن دراسة البقعة المضيئة عن قرب وتسمى قرص إيرى Airy Disk - بعبارة أخرى - دراسة توزيع الإضاءة على الحائل - تظهر وجود هدب مضيئة وأخرى مظلمة كما في الشكل (۲-۷). قرص إيرى اشعة متوازية من المصدر البقعة الثانوية المعنية الأولى مطابع زمزم شكل (۲ - ۷) الحيود على فتحة دائرية ۲۹ الفيزياء الصف الثانى الثانوى

مثال ص29/ احسب الطول الموجي للضوء الاحادي اللون الامستخدم
حيود الضوء
الوحدة الأولى الموجات الفصل الأول الضوء ويوضح الشكل (۲-۸) الحيود علي فتحة مستطيلة بينما يوضح الشكل (۲-۹) نماذج مختلفة للحيود علي حدود فاصلة للمادة. وبصفة عامة يظهر الحيود بوضوح إذا كان الطول الموجي مقارباً لأبعاد فتحة العائق والعكس صحيح. وجدير بالذكر انه لا يوجد فرق جوهري بين نموذجي التداخل والحيود ، فكل منهما ينشأ من تراكب موجات. شق مستطيل شعاع ضوئي شكل (۲ - ۸) الحيود على فتحة مستطيلة منتصف الهدية المضيئة المركزية شده الاصابة شكل (۲ - ۹) توزيع شدة الإضاءة على الحائل مع تتابع الهدب الناشئة من الحيود على فتحة مستطيلة الضوء حركة موجية يتضح لنا من الفقرات السابقة أن الضوء 1 - ينتشر في خطوط مستقيمة. ٢- ينعكس وفقاً لقانوني الانعكاس. 3- ينكسر وفقاً لقانوني الانكسار. 4- يتداخل الضوء وينشأ عن التداخل تقوية في شدة الضوء في بعض المواضع (هدب مضيئة) وانعدام في شدة الضوء فى بعض المواضع الأخرى (هدب مظلمة). ه - يحيد الضوء عن مساره إذا اصطدم بعائق. - وهذه هي نفس الخصائص العامة للموجات، وبالتالي يكون الضوء حركة موجية. الفيزياء الصف الثانى الثانوى ۳۰ ۲۰۲۰ - ۲۰۱۹

تابع حيود الضوء
الضوء حركة موجية
الوحدة الأولى الموجات الفصل الثاني الإنعكاس الكلي والزاوية الحرجة عندما ينتقل شعاع ضوئي من وسط أكبر كثافة ضوئية كالماء أو الزجاج ) إلى وسط أقل كثافة ضوئية كالهواء، فإن الشعاع المنكسر يبتعد عن العمود كما في الشكل التالى (۲-۱۰ ) . ومع زيادة قيمة زاوية السقوط في الوسط الأكبر كثافة ضوئية ( معامل انكسار مطلق كبير) تزداد قيمة زاوية الإنكسار في الوسط الأقل كثافة ضوئية (معامل إنكسار مطلق صغير). #2 شكل (۲) - (١٠) سقوط ضوء من وسط أكبر كثافة ضوئية إلى وسط أقل كثافة ضوئية وعندما تبلغ زاوية السقوط في الوسط الأكبر كثافة ضوئية قيمة معينة ( عندها تبلغ زاوية الإنكسار في الوسط الأقل كثافة اكبر قيمة لها وتساوي 90. وعندها يخرج الشعاع المنكسر مماساً للسطح الفاصل. وتسمى زاوية السقوط في هذه الحالة الزاوية الحرجة ( وهى زاوية سقوط في الوسط الأكبر كثافة ضوئية تقابلها زاوية انكسار فى الوسط الأقل كثافة ضوئية تساوى .90° بتطبيق قانون سئل في هذه الحالة: ومنها n, sin Q = n, sin 90* n₂ sin c = = 112 (2-6) حيث معامل انكسار الوسط الأكبر كثافة ضوئية ، n معامل انكسار الوسط الأقل كثافة ضوئية ، الزاوية الحرجة. مطابع زمزم ۳۱ الفيزياء الصف الثانى الثانوى

الإنعكاس الكلي والزاوي الحرجة
الوحدة الأولى الموجات الفصل الأول الضوء وعندما يكون الوسط الأقل كثافة ضوئية هو الهواء يكون 1 ،n، وعندئذ تكتب العلاقة السابقة على الصورة : ny sin Q = 1 (2-7) n₁ = sin c حيث n معامل الانكسار المطلق للوسط الأكبر كثافة ضوئية وبذلك يمكن حساب معامل انكسار الوسط بمعرفة الزاوية الحرجة له . وإذا زادت قيمة زاوية السقوط فى الوسط الأكبر كثافة ضوئية عن الزاوية الحرجة فإن الشعاع الضوئي لا ينفذ إلى الوسط الثانى الأقل كثافة ضوئية، وإنما ينعكس انعكاسا كليا في نفس الوسط، على خلاف أي زاوية سقوط أخرى أقل من الزاوية الحرجة ، حيث ينفذ جزء من الضوء وينعكس جزء آخر كما في الصورة الموضحة (شكل ۲ – ۱۰ جـ ، د ) امثلة منهما . الحل 1 - إذا كان معاملا انكسار الزجاج والماء هما 1.6 و 1.33 علي الترتيب، فاحسب الزاوية الحرجة لكل في حالة الزجاج 1 n₁ = sin C sin = 1 = 1 1.6 = 0.625 ومنها: "41 38 = 0 في حالة الماء: ومنها 1 = = 0.7518 1.33 sing = ոլ 0 = 48° 45 1 الفيزياء الصف الثانى الثانوى ۳۲ ۲۰۲۰ - ۲۰۱۹

تابع الإنعكاس الكلي والزاوي الحرجة
أمثلة ص32/ فاحسب الزواية الحرجه لكل منهما
الموجات الفصل الثاني الضوء الوحدة الأولى ۲ - مستخدما البيانات المعطاة فى المثال السابق احسب الزاوية الحرجة للضوء الساقط من الزجاج إلى الماء الحل باستخدام قانون سنل ومنها , sin 90" = ny sin Qa 1.33 x 1 = 1.6 sin Q 1 x 1.33 sin c = = 0.8313 1.6 =56°14' بعض تطبيقات الإنعكاس الكلي أولا : الألياف الضوئية البصرية Fiber optics (Optical fibers: ويوضح الشكل (۲-۱۱) ليفة ضوئية - وهى قضيب مصمت رفيع من مادة شفافة-إذا دخل الضوء من أحد طرفيها فإنه يعاني إنعكاسات كلية متتالية (زاوية السقوط أكبر من الزاوية الحرجة) حتى يخرج من طرفها الأخر شكل (۲-۱۲). ويوضح الشكل (۱۳۲) حزمة مكونة من الاف الياف معاً تتكون منها حزمة مرنة قابلة للانثناء، بحيث تصل إلي أماكن يصعب الوصول إليها ويمكن استخدامها في نقل الضوء بدون فقد يذكر. وتلقي الألياف الضوئية الآن اهتماماً كبيراً. فالليفة الضوئية أو البصرية تستخدم الأن في الفحوص الطبية شكل (۲) - ۱۱) الألياف تحافظ على مثل المناظير الطبية Endoscopes شكل (۱۳۲) والتي تستخدم في الشعاع رغم انثناء الألياف التشخيص كما تستخدم في إجراء العمليات الجراحية باستخدام شعاع الليزر كما يستخدم الليزر في الإتصالات عن طريق تحويل الإشارات الكهربية إلى ومضات ضوئية في كابل من الألياف الضوئية. 90-0 شكل (۲) - (١٢) ألياف ضوئية و شعاع شعاع ؟ مطابع زمزم ۳۳ الفيزياء الصف الثانى الثانوى
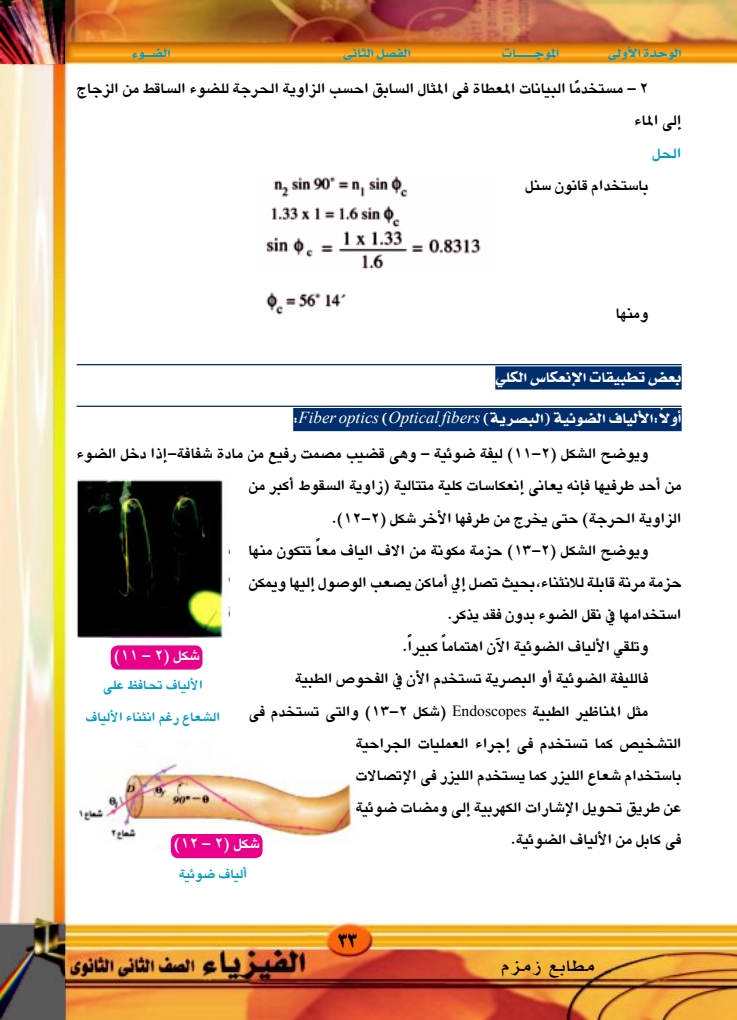
تابع مثال ص33
بعض تطبيقات الإنعكاس الكلي
الوحدة الأولى الموجات الفصل الأول e Q OR الضوئية الضوء الداخل شكل (۲) - (۱۳) ألياف ضوئية (i) الضو ليفة ضوئية الضوء الخارج كيف تعمل الألياف الضوئية شكل (۲) - (۱۳) إجراء عمليات جراحية باستخدام المناظير الطبية إذا كان لدينا أنبوبة مجوفة، ونظرنا من أحد طرفيها لنرى جسماً مضيئاً في الطرف الآخر، فإنه يمكن رؤيته. أما إذا حدث انثناء للأنبوبة المجوفة ، فلا يمكن رؤية الجسم المضيء. وفي هذه الحالة كيف يمكن رؤيته ؟ إذا وضعنا مرايا عاكسة عند مواضع مسار الشعاع الضوئي فإننا نستطيع فى هذه الحالة رؤية الجسم المضيء. وبالمثل يمكن استخدام الألياف الضوئية عند سقوط شعاع الفيزياء الصف الثانى الثانوى ٣٤ ۲۰۲۰ - ۲۰۱۹
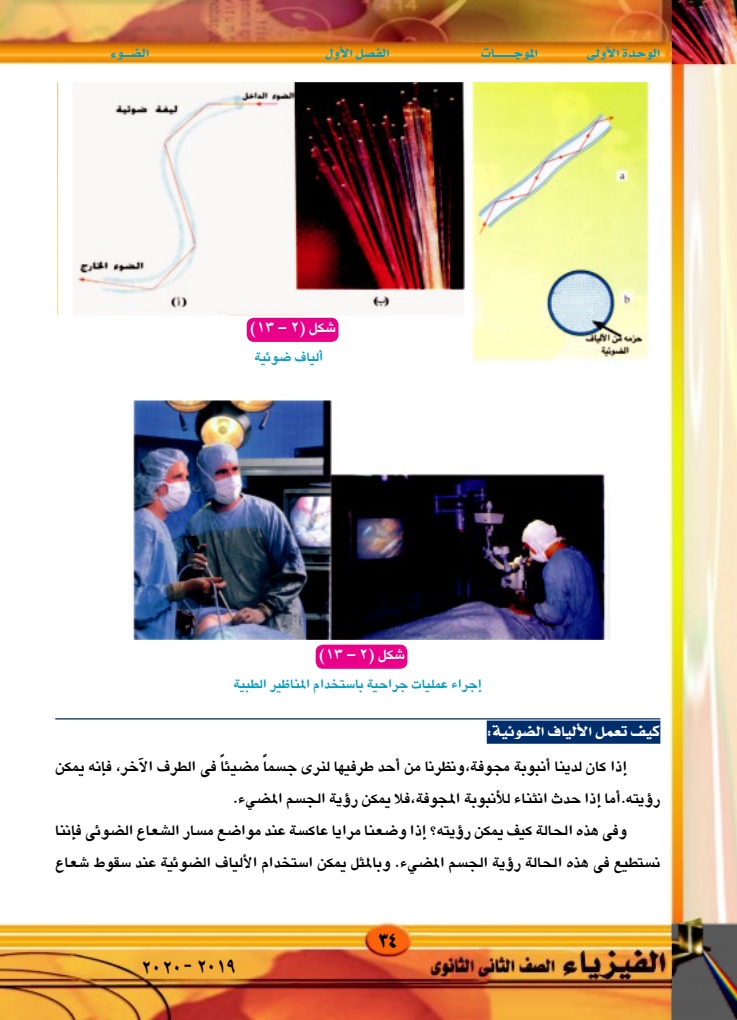
شكل (2-13)
كيف تعمل الألياف الضوئية
الوحدة الأولى الموجات الفصل الثاني الضوء ضوئي بزاوية سقوط أكبر من الزاوية الحرجة فإنه يحدث إنعكاسات كلية ليخرج الشعاع بكامل طاقته من الطرف الآخر رغم انثناء هذه الألياف. ثانيا : المنشور العاكس نظراً لأن الزاوية الحرجة بين زجاج معامل إنكساره المطلق (15) والهواء حوالي 420 فإن منشوراً ثلاثياً من الزجاج زواياه (45،45,90) يستخدم فى تغيير مسار حزمة ضوئية بمقدار 90 أو 180.ومثل هذا المنشور يستخدم فى بعض الأجهزة البصرية مثل البيروسكوب Periscope الذي يستخدم في الغواصات البحرية وفي مناظير الميدان Binoculars شكل (1) زجاج 45 هواء ب المنشور العاكس يغير مسار الضوء 180 ج استخدام المنشور في منظار الميدان شكل ( ٢ - (١٤) المنشور العاكس واستخدام المنشور لهذا الغرض أفضل من إستخدام السطح المعدنى العاكس (أو المرآة). أولاً : لأن الضوء ينعكس فى المنشور إنعكاساً كلياً. ومن النادر أن يتواجد السطح المعدني العاكس الذي تبلغ كفائته ۱۰۰٪. ثانياً: يتعرض السطح المعدنى لما يفقده بريقه أو لمعانه، فتقل قابليته لعكس الضوء، ولا يحدث مثل هذا في المنشور. صحيح أن جزئاً أو نسبة من الضوء تفقد عند دخوله أو خروجه من المنشور ، ولكن يمكن تجنبها بتغطية السطح الذي يدخل منه الضوء أو يخرج منه بغشاء رقيق غير عاكس مثل فلوريد الألومنيوم وفلوريد الماغنيسيوم (معامل انكساره أقل من معامل انكسار الزجاج). مطابع زمزم ۳۵ الفيزياء الصف الثانى الثانوى |
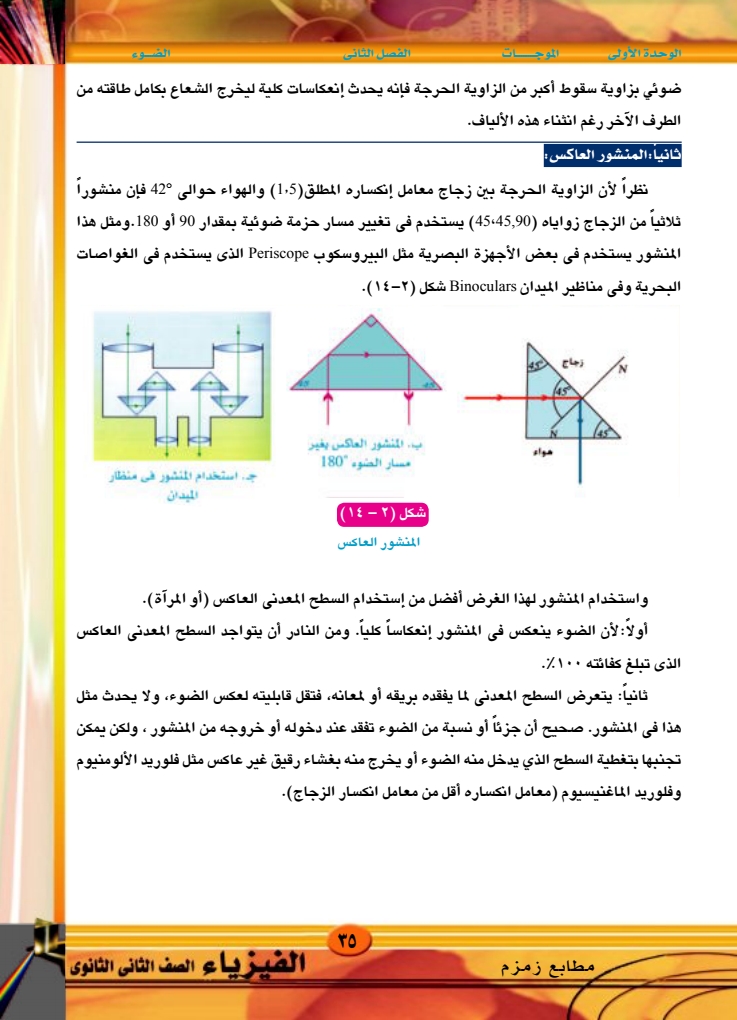
ثانياً المنشور العاكس
تابع كيف تعمل الالياف الضوائية
الوحدة الأولى الموجات الفصل الأول الضوء ثالثا: السراب السراب ظاهرة مألوفة في الأيام القائظة شديدة الحرارة) ويمكن رؤيتها صيفاً في الطرق حيث يبدو الطريق لراكب السيارة كما لو كان مغطى بالماء شكل (٢-١٥) ، وكما يمكن ملاحظتها في الصحاري حيث ترى للنخيل أو التلال صورا مقلوبة شبيهة بتلك الصور التي تحدث بالإنعكاس عن سطح الماء، وعندئذ يظن المراقب وجود الماء شكل (٢-١٥ ب). B شكل ( ٢ - ١١٥) شكل ( ٢ - ١٥ ب) الطرق الممهدة تبدو مبللة انعكاس السماء في الصحراء يوحي بوجود ماء وتفسر هذه الظاهرة كما يلى: في الأيام الشديدة الحرارة ترتفع درجة حرارة الطبقات الهوائية الملاصقة لسطح الأرض فتقل كثافتها عن كثافة الطبقات التي تعلوها ويترتب على ذلك أن تكون معاملات انكسار طبقات الهواء العليا أكبر من تلك التي تحتها. لذلك إذا تتبعنا شعاعاً ضوئياً صادراً من قمة نخلة مثلاً فإن هذا الشعاع عند انتقاله من الطبقة العليا إلى الطبقة التي تقع تحتها ينكسر مبتعدا عن العمود. وعند إنتقاله من هذه الطبقة إلى التي تليها يزداد انحرافه. وهكذا يزداد انحراف الشعاع أثناء انتقاله خلال طبقات الهواء المتتالية متخذا مسارًا منحنيا، وعندما تصبح زاوية سقوطه في إحدى الطبقات أكبر من الزاوية الحرجة بالنسبة للطبقة التى تحتها، فإن الشعاع الضوئي ينعكس انعكاسا كليا متخذا مسارا منحنيا إلى أعلى حتى يصل إلى العين التي ترى صورة قمة النخلة على امتداد الشعاع الذي يصلها ، وهذا يفسر رؤية صورتها مقلوبة ( شكل ٢ - ١٥ ب) فيظن المراقب أن هناك ماء. الفيزياء الصف الثانى الثانوى ٣٦ ۲۰۲۰ - ۲۰۱۹
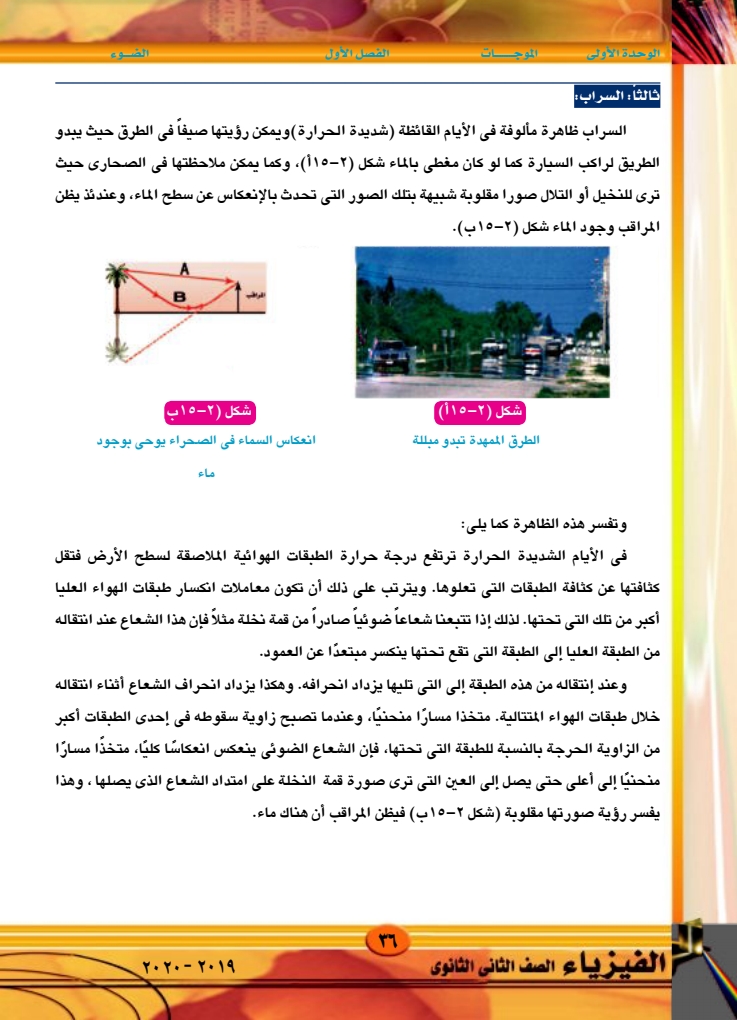
ثالثاً السراب
الوحدة الأولى الموجات الفصل الثاني إنحراف الضوء في المنشور الثلاثي عندما يسقط شعاع ضوئي مثل الشعاع (ab) على الوجه (XY) لمنشور ثلاثى فإن هذا الشعاع ينكسر داخل المنشور متخذا المسار (bc) حتى يسقط على الوجه (X) كما في الشكل (٢-١٦) فيخرج إلى الوسط الأول في الاتجاه (cd) ومن هذا الشكل نتبين أن الشعاع الضوئي فى المنشور الثلاثي ينكسر مرتين، إحداهما عند الوجه الأول (XY) والأخرى عند الوجه الثانى (XZ) ونتيجة لذلك ينحرف الشعاع عن مساره بزاوية معينة هي زاوية الإنحراف .. زاوية الانحراف Deviation Angle : هي الزاوية الحادة المحصورة بين امتدادى الشعاع الساقط والشعاع الخارج ويرمز لها هنا بالرمز .. وإذا كانت زاوية السقوط هي 1 وزاوية الانكسار عند الوجه الأول هى 6 وزاوية السقوط على الوجه الثاني هي ؟ وزاوية الخروج هي 9 وزاوية رأس المنشور A ، فإننا نتبين من هندسة الشكل ٢-١٦ ما يلى: P شكل (٢) - (١٦) مسار شعاع الضوء في منشور ثلاثي α=(01-01)+ (02-02) a = (1 + 02) - ( 01 + 2 ) حيث أن مجموع زوايا الشكل الرباعي bxce هو 2 والزاويتين b و c قائمتان فإن الزاوية : هي (180) وفي المثلث bce مجموع الزوايا °180 وعلى ذلك فإن : 01 +02 = 180-(180-A) = A (2-8) وبالتعويض من المعادلة (8-3) نجد أن : مطابع زمزم a = 1 + 62- A (2-9) ۳۷ الفيزياء الصف الثانى الثانوى

إنحراف الضوء في المنشور الثلاثي
الوحدة الأولى الموج بات الفصل الأول الضوء ومن هذه العلاقة نتبين أن زاوية الانحراف في منشور ثلاثى زاوية رأسه °A تتوقف علي زاوية السقوط . ويمكن عمليا بيان أن زاوية الانحراف تتناقص تدريجيا مع ازدياد زاوية السقوط حتى تصل زاوية الانحراف إلى حد معين يعرف بالنهاية الصغرى للإنحراف ، بعده تأخذ زاوية الانحراف في الازدياد تدريجيا مع ازدياد زاوية السقوط كما في الشكل (۲ - ۱۷) وفي وضع النهاية الصغرى للانحراف يمكن عمليا ونظريا اثبات أن: 0=02 = زاوية الانحراف C وتصبح العلاقتان (8-2) و (9-2) كما يلى ومنها ومنها ولكن العلاقة A=20 슬 α=20-A %+ A 2 sin n= sin 0 زاوية السقوط شكل (۲) - (۱۷) زاوية الانحراف لها نهاية صغرى بالتعويض عن ( 6 نجد أن معامل الانكسار للمنشور في وضع النهاية الصغرى للانحراف يتعين من at A sin 2 n = (2-10) sin A2 الفيزياء الصف الثانى الثانوى ۳۸ ۲۰۲۰ - ۲۰۱۹

تابع إنحراف الضوء في المنشور الثلاثي
الوحدة الأولى الموجات الفصل الثاني تجربة عملية : تعيين مسار شعاع ضوئى خلال منشور زجاجي واستنتاج قوانين المنشور الأدوات المطلوبة منشور من الزجاج زاوية رأسه °60 - دبابيس – منقلة – مسطرة. خطوات العمل : ۱ - ضع المنشور على ورقة بيضاء وحدد قاعدته المثلثة - ثم ابعد المنشور وارسم خطا (ab) مائلا على أحد وجهي المنشور يمثل شعاعًا ساقطًا بزاوية سقوط معينة. ضع المنشور في موضعه ، ثم انظر من الجانب المقابل ، وحدد موضع الشعاع الخارج (cd) بالاستعانة بالدبابيس ، أو بوضع مسطرة والنظر بحيث تصبح حافة المسطرة على امتداد صورة الشعاع الساقط (ab) ثم ارسم خطًا (cd) في محاذاة حافة المسطرة، تجد أن هذا الخط يقع على امتداد صورة الخط الأول . ۲ - ارفع المنشور ثم صل (bc) فيكون مسار الشعاع دیوسان منطبقان على صورة الشعاع عند الضوئي هو (abcd) من الهواء إلى الزجاج إلى الهواء النظر إليه من الوجه الآخر المنشور ثانية. - مد الشعاع الخارج (cd) على استقامته حتى يقابل امتداد الشعاع الساقط (ab) فتكون الزاوية المحصورة بينهما هي زاوية الانحراف شكل ۲-۱۸) - قس كلا من زاوية السقوط ، وزاوية الانكسار ، وزاوية السقوط الداخلية ) ، وزاوية الخروج وزاوية الانحراف » مسار الشعاع الخارج) شكل (۲) - (۱۸) مسار شعاع الضوء في منشور ثلاثى ه - كرر العمل السابق عدة مرات بتغيير زاوية السقوط وضع النتائج في جدول زاوية رأس زاوية السقوط زاوية الانكسار زاوية السقوط زاوية الخروج زاوية المنشور A الداخلية . 02 الانحراف » استخدم المعادلتين (8-2) و (9-2) لحساب قيمتي» ،A ، وطابق النتائج بالقيم المقاسه عمليًّا. مطابع زمزم ۳۹ الفيزياء الصف الثانى الثانوى

تجربة عملية تعيين مسار شعاع ضوئي خلال منشور زجاجي
الوحدة الأولى الموجات الفصل الأول الضوء تفريق الضوء بواسطة المنشور الثلاثي Dispersion استنتجنا في الفقرة السابقة إنه فى وضع النهاية الصغرى للانحراف يتعين معامل انكسار مادة المنشور من العلاقة : at A sin 2 n= A sin حيث n معامل الانكسار لمادة المنشور، ما هي النهاية الصغرى للإنحراف ، A زاوية رأس المنشور. ونظرا لأن زاوية رأس المنشور ثابتة فإننا نتبين أن تغير معامل الانكسار يتبعه تغير في قيمة زاوية النهاية الصغرى للانحراف فبزيادة معامل الانكسار تزداد قيمة النهاية الصغرى للانحراف والعكس صحيح. ونظرا لأن معامل الانكسار n يتوقف على الطول الموجي للضوء المار من خلال المنشور، فإن زاوية النهاية الصغرى للانحراف تتوقف بدورها على الطول الموجي . لذلك إذا سقطت حزمة ضوء أبيض على منشور ثلاثى مهيأ في وضع النهاية الصغرى للانحراف فإن الضوء الخارج من المنشور يتفرق إلى ألوان الطيف المعروفة كما في الشكل (19-r) ومن الشكل نتبين أن أشعة الضوء البنفسجى تكون أكثر الأشعة انحرافا (معامل انكسارها أكبر)، وأن أشعة الضوء الأحمر تكون أقل الأشعة انحرافا (معامل انكسارها أصغر). وألوان الطيف المرئى التى يتفرق إليها الضوء الأبيض هي بالترتيب ) من جهة رأس المنشور إلى قاعدته ) : . شكل (۲) - (۱۹) المنشور يفرق ألوان الطيف الأحمر – البرتقالي - الأصفر - الأخضر - الأزرق - النيلي - البنفسجي. تعميق المعرفة لتعميق معرفتك في هذا الموضوع يمكنك الاستعانة بينك المعرفة المصري من خلال الرابط المقابل الفيزياء الصف الثانى الثانوى ۲۰۲۰ - ۲۰۱۹

تفريق الضوء بواسطة المنشور الثلاثي
الوحدة الأولى الموج بات الفصل الثاني المنشور الرقيق هو عبارة عن منشور ثلاثى من الزجاج مثلاً، زاوية رأسه صغيرة لا تتجاوز عدة درجات ويكون دائما في وضع النهاية الصغرى للانحراف أى أن معامل انكسار مادة المنشور يحسب من العلاقة : at A sin 2 n= sin ونظرا لان ) وكذلك 2 مى 2 A بالتقدير الدائرى . وعلى ذلك يكون الآتية: وكذلك هي زوايا صغيرة ، يكون جيب الزاوية مساويا لقيمة الزاوية (2) sin(A)=(A) 2 sin وبالتعويض عنهما في العلاقة السابقة نجد أن معامل انكسار مادة المنشور الرقيق يتعين من العلاقة n = Co+A (2-11) A Co= A (n - 1) (2-12) قوة التفريق اللونى Dispersive Power عند سقوط ضوء أبيض على منشور ثلاثى يتفرق هذا الضوء إلى ألوان الطيف المعروفة ويرجع هذا إلى اختلاف معاملات الإنكسار تبعًا لاختلاف أطوالها الموجية (a) A (n-1) (αo)b=A (n-1) حيث A زاوية رأس المنشور الرقيق ، . معامل انكسار مادته للضوء الأحمر ، n معامل انكسار مادته للضوء الأزرق. مطابع زمزم ٤١ الفيزياء الصف الثانى الثانوى |
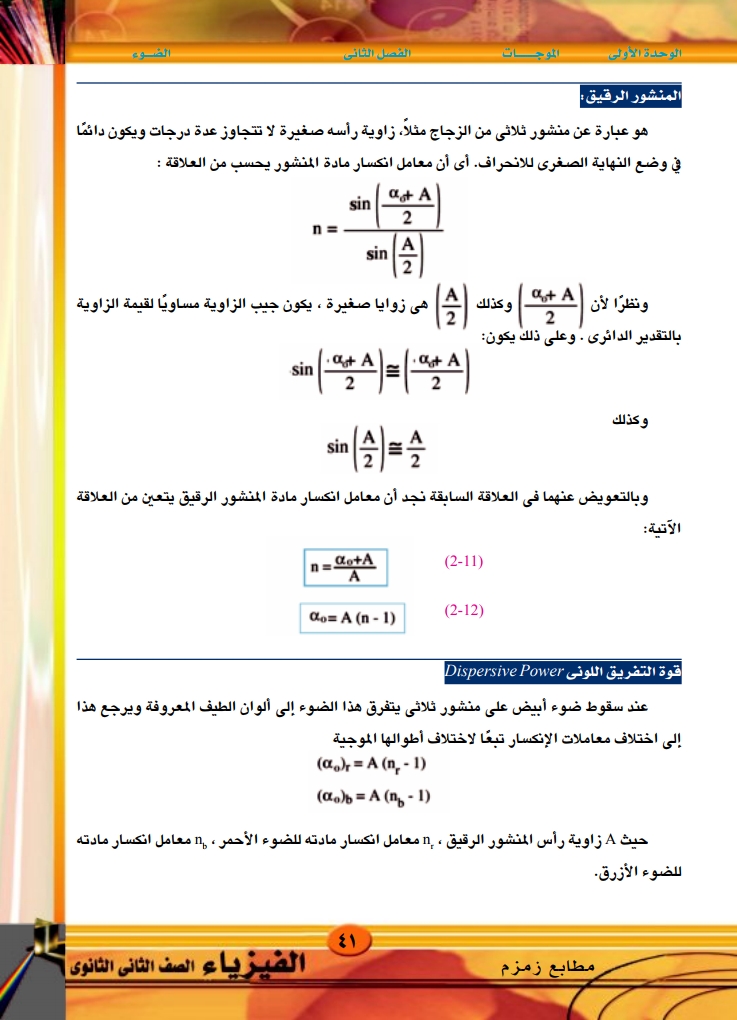
المنشور الرقيق
قوة التفريق اللوني
الضوء الوحدة الأولى الموجات الفصل الأول بالطرح نجد أن aab - adr = A (2-13) يمثل الطرف الأيسر ما نسميه بالانفراج الزاوى بين الشعاعين الأزرق والأحمر ، وبالنسبة للضوء الأصفر الذي يتوسط اللونين الأحمر والأزرق) تكون زاوية انحرافه فى المنشور الرقيق هي : (α)y=A (ny- 1) (2-14) حيث n معامل انكسار مادة المنشور للضوء الأصفر فإذا كانت ( (a) متوسط (a) ، (a) 00α- (a)b-(αo)r (do)y n - n, ny-1 (2-15) فإن متوسط وبالقسمة نجد أن وتسمى ( قوة التفريق اللونى Dispresive Power وهي كما نرى لا تتوقف على زاوية رأس المنشور. ٤٢ ۲۰۲۰ - ۲۰۱۹ الفيزياء الصف الثانى الثانوى

تابع قوة التفريق اللوني
الوحدة الأولى الموج ات الفصل الثاني تلخيص: . قانونا انعكاس الضوء (۱) زاوية السقوط = زاوية الإنعكاس. (۲) الشعاع الضوئى الساقط، والشعاع الضوئى المنعكس، والعمود المقام من نقطة السقوط على السطح العاكس تقع جميعها في مستوى واحد عمودى على السطح العاكس. . يغير الضوء من اتجاه انتشاره عند انتقاله من وسط إلى وسط آخر بسبب اختلاف سرعة الضوء في الوسط الثاني 7 عن سرعته فى الوسط الأول ٧ . ويخضع الضوء في انكساره لما يلي: (۱) نسبة جيب زاوية السقوط فى الوسط الأول إلى جيب زاوية فى الوسط الثاني نسبة ثابتة لهذين الوسطين، تسمى معامل الانكسار النسبى من الوسط الأول إلى الوسط الثاني، ويرمز لها بالرمز 1112= sin sin e حيث ( زاوية السقوط فى الوسط الأول ، و زاوية الانكسار في الوسط الثاني (۲) الشعاع الضوئي الساقط والشعاع الضوئى المنكسر والعمود المقام من نقطة السقوط على السطح الفاصل تقع جميعها في مستوى واحد عمودى على السطح الفاصل. . معامل الانكسار من الوسط الأول إلى الوسط الثانى هو نسبة سرعة الضوء 7 في الوسط الأول إلى سرعة الضوء 7 في الوسط الثاني أي أن: V₂ وهذه صورة أخرى لمعامل النسبي بين وسطين. • معامل الانكسار المطلق لوسط هو n= أي هو نسبة سرعة الضوء في الفراغ إلى سرعة الضوء في الوسط. • قانون سنل للضوء ينص على : حاصل ضرب معامل الإنكسار المطلق لوسط السقوط في جيب زاوية السقوط يساوى معامل الإنكسار المطلق لوسط الإنكسار فى جيب زاوية الإنكسار. مطابع زمزم n₁sino= sing ٤٣ الفيزياء الصف الثانى الثانوى |

تلخيص
الوحدة الأولى الموجات الفصل الأول الضوء . في تجربة ينج تتعين المسافة بين أى هدبتين متتاليتين من نفس النوع (مضيئتين أو مظلمتين) من العلاقة : Ay= AR d حيث طول موجة الضوء المستخدم ، R المسافة بين الحائل المعد لاستقبال الهدب والحاجز ذي الشق المزدوج، d المسافة بين الشقين. . الضوء حركة موجية . الزاوية الحرجة : هي زاوية سقوط في الوسط الأكبر كثافة ضوئية تقابلها زاوية انكسار في الوسط الأقل كثافة ضوئية مقدارها 900 . معامل الانكسار المطلق لوسط يساوى مقلوب جيب الزاوية الحرجة له عند انتقال الضوء من هذا الوسط إلى الهواء أو الفراغ. 1 sinc n = . الانعكاس الكلى : عندما تكون زاوية سقوط الضوء فى الوسط الأكبر كثافة ضوئية أكبر من الزاوية الحرجة، فإن الضوء لا ينفذ إلى الوسط الأقل كثافة ضوئية وإنما ينعكس عند السطح الفاصل انعكاسا كليا. . السراب ظاهرة تنتج عن الانعكاس الكلى. • زاوية رأس المنشور الثلاثي 2 + 1 = A . زاوية الانحراف » هي الزاوية الحادة المحصورة بين امتدادى الشعاعين الساقط والخارج وتتعين من العلاقة a = ( + ) - A حيث زاوية السقوط ، زاوية الخروج ، A زاوية رأس المنشور. . فى وضع النهاية الصغرى للانحراف يكون : الفيزياء الصف الثانى الثانوى 0-02-00 ٤٤ ۲۰۲۰ - ۲۰۱۹

تابع تلخيص1
الوحدة الأولى الموج ات يتعين معامل انكسار مادة المنشور من العلاقة : الفصل الثاني α + A sin 2 n = A sin حيث n معامل الانكسار، زاوية الانحراف فى وضع النهاية الصغرى ، A زاوية رأس المنشور. . يتعين الانحراف فى المنشور الرقيق من العلاقة : de = A (n - 1) . الانفراج الزاوى فى المنشور الرقيق يحسب من ناتج الطرح (cob - (cor حيث (a) زاوية انحراف الأشعة الزرقاء، ( (a) زاوية انحراف الأشعة الحمراء . قوة التفريق اللوني (0) هي : حيث 00α= (a)b-(αo)r (do)y a = n nb-nr -1 هي معامل انكسار مادة المنشور للون الأزرق. n معامل انكسار مادة المنشور للون الأحمر. معامل انكسار مادة المنشور للون الأصفر. مطابع زمزم ٤٥ الفيزياء الصف الثانى الثانوى |

تابع تلخيص2






