الرياضيات العامة 1
الوحدة الأولى: الدوال الحقيقية ورسم المنحنيات
الدرس الخامس: حل معادلات ومتباينات القيمة المطلقة
حل معادلات ومتباينات القيمة المطلقة - الرياضيات العامة 1 - ثاني ثانوي
الوحدة الأولى: الدوال الحقيقية ورسم المنحنيات
الوحدة الثانية: الأسس واللوغاريتمات وتطبيقات عليها
الوحدة الثالثة: النهايات
الوحدة الرابعة: حساب المثلثات

أولاً: حل المعادلات
حل المعادلة : س- 3 = 4 بيانيا وجبريا

المنحنيين يتقاطعان في النقطتين (-1, 4) (7, 4 )
بعض خواص مقياس العدد
حل المعادلة س - 3 = 2 س + 1 بيانيا

تابع مثال2
أوجد جبريا مجموعة الحل لكل من المعادلات الآتية
أوجد جبريا مجموعة الحل لكل من المعدلات الآتية
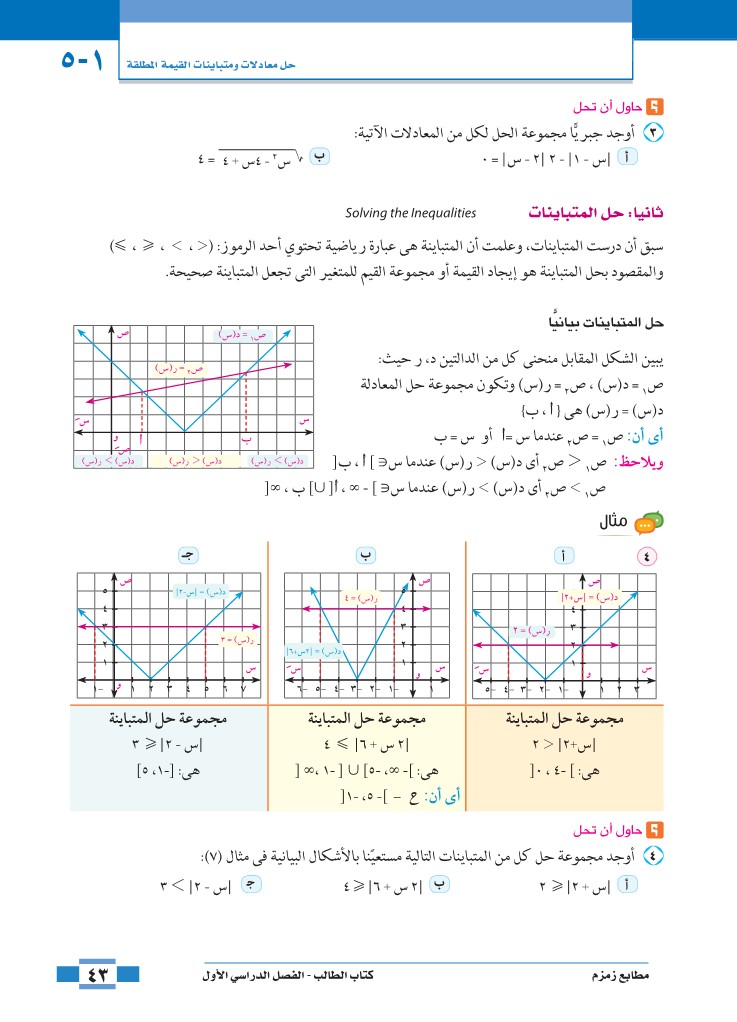
ثانياً: حل المتباينات
أوجد مجموعة حل كل من المتباينات التالية مستعينا بالأشكال البيانية في مثال7

حل المتباينات جبرياً
أوجد على صورة فترة مجموعة حل كل من المتباينات الآتية

يفرض أن درجة الحرارة المحتمل تسجيلها على مدينة القاهرة في هذا اليوم = س
مثال7 وظائف خالية

طريقان الأول يمثله منحنى الدالة د حيث د(س) = س -4 والثاني يمثله منحنى الدالة ر حيث ر (س) =3
اكتب متباينة القيمة المطلقة التي تعبر عن درجة حرارة مقاسة بالترمومتر الطبي وتتراوح بين 35 , 42
أوجد جبريا مجموعة الحل لكل من المتباينات الآتية
أوجد بيانيا مجموعة الحل لكل من المتباينات الآتية
,جد بيانيا مجموعة لحل لكل من المعادلات الآتية
أوجدجبريا مجموعة الحل لكل من المعادلات الاتية
اختر منةالقائمة التالية مجموعة الحل المناسبة لكل من معادلة أو متباينة مما ياتي
أكمل ما يأتي

عنوان جديد الدالة
اختبار الخط الرأسي
دالة متعددة التعريف
اطراد الدوال
الدوال الزوجية والفردية
خواص هامة
الدالة الخطية
الدالة التكعيبية
دالة المقياس

الدالة الكسرية
التحويلات الهندسية للدالة د حيث ص = (س) أ > 0 تحدد بالآتي
خواص مقياس العدد
حل المعادلة لأي دالتين د , ر تكون مجموعة حل المعادلة تكون مجموعة حل المعادلة د (س) = ر (س) هي مجموعة الإحداثيات السينية
حل المتباينة : هو إيجاد مجموعة قيم المتغير التي تجعل المتباينة صحيحة

أوجد جبريا مجموعة حل كل من المعادلات والمتباينات الآتية
أوجد بيانيا مجموعة حل كل من
إذا كانت الدالة د حيث د (س )= 1/س+1 أوجد مجال الدالة ونقطة التماثل لمنحنى هذه الدالة
استخدم منحنى الدالة د حيث د ()= 1/س لتمثيل الدالة ر حيث ر (س)= د (س )+ 2 ثم اكتب نقطة تماثل الدالة
ارسم منحنى الدالة د حيث د ()= (س -1 ) واستنتج من الرسم مدى الدالة واطرادها وبين نوعها من حيث كونها زوجية أو فردية أو غير ذلك
في الشكل المقابل اكتب احداثي نقطة رأس المنحنى
ارسم منحنى الدالة د حيث د (س) =س
استخدم منحنى الدالة د حيث د(س) = س لتمثيل الدالة ر حيث ر (س) =( س-1 )- 2 ثم أ وجد مدى الدالة ر
ارسم منحنى الدالة حيث د ()س = س + 1 , ر (س) = 5 ومن الرسم أوجد






