نماذج اختبارات الجبر والهندسة - رياضيات 1 - ثالث اعدادي
الوحدة الأولى: العلاقات والدوال
الوحدة الثانية: النسبة والتناسب والتغير الطردي والتغير العكسي
الوحدة الرابعة: حساب المثلثات
الوحدة الخامسة: الهندسة التحليلية
كتاب النشاط
الأنشطة والتدريبات
الوحدة الأولى: العلاقات والدوال
الوحدة الثانية: النسبة والتناسب والتغير الطردي والتغير العكسي
الوحدة الرابعة: حساب المثلثات

السؤال الأول : أ ختر الإجابة الصحيحة من بين الإجابات المعطاة
بدون أستخدام الآلة الحاسبة أثبت أن جا 60 = 2 جا 30 جنا30
إذا كانت 4 حتا 60 جا 30= طاس فأوجد قيم س حيث س زاوية حادة

إذا كان المستقيم ل1يمر بالنقطتين () () والمستقيم ل1 يصنع مع الاتجاه الموجب لمحور السينات زاوية قياسها45 فأوجد قيمة ك إذا كان ل1 يوازي ل2
أوجد معادلة المستقيم الذي ميلة 2 ويمر بالنقطة (1, 0)
ا ب ج مثلث قائم الزاوية في ج فيه أ ج = 6 سم ب ج = 8 سم أوجد
أثبت أن النقط أ (3.-1 ) ب (-4, 6) ج (2,-2) الواقعة في مستوى إحداثي متعامد تمر بها دائرة واحدة مركزها النقطة م ( -1 .2 ) ثم أوجد محيط الدائرة

2جا 30 ظا 60
أوجد معادلة المستقيم المار بالنقطتين (), () ثم أثبت أنه يمر بالنقطة الأصل
إذا كان جتاه ظا30 =جنا 45 فأوجد ق الزاوية ه حيثه زاوية حادة
إذا كان المستقيمان ميلالهما - 3/2 ,6/ك متوازيان فإن ك =
البعد العمودي بين المستقيمين س-2=0س +3 =0 يساوي
دائرة مركزها نقطة جديدة
إذا كان جتا س = جذر 2 /2 س زاوية حادة فإن جا2س=
معادلة المستقيم المار بالنقطة () ويوازي محور السينات هي

أوجد معادلة مستقيم الذي يقطع من محوري الإحداثيات السيني والصادي جزءين موجبين طولايهما 1, 4 وحدات طول على الترتيب ثم أوجد ميل هذا المستقيم
أ ب ج مثلث قائم الزاوية في ب فيه أ ج =10 سم ,ب ج =8 سم
أثبت أن المستقيم المار بالنقطتين (-1 . 3) (2, 4) يوازي المستقيم 3 ص - س -1=0

ضع علامة صح أمام العبارة الصحيحة وعلامة خطأ أمام العبارة الخاطئة
أختر اإجابة الصحيحة من بين الإجابات المعطاة
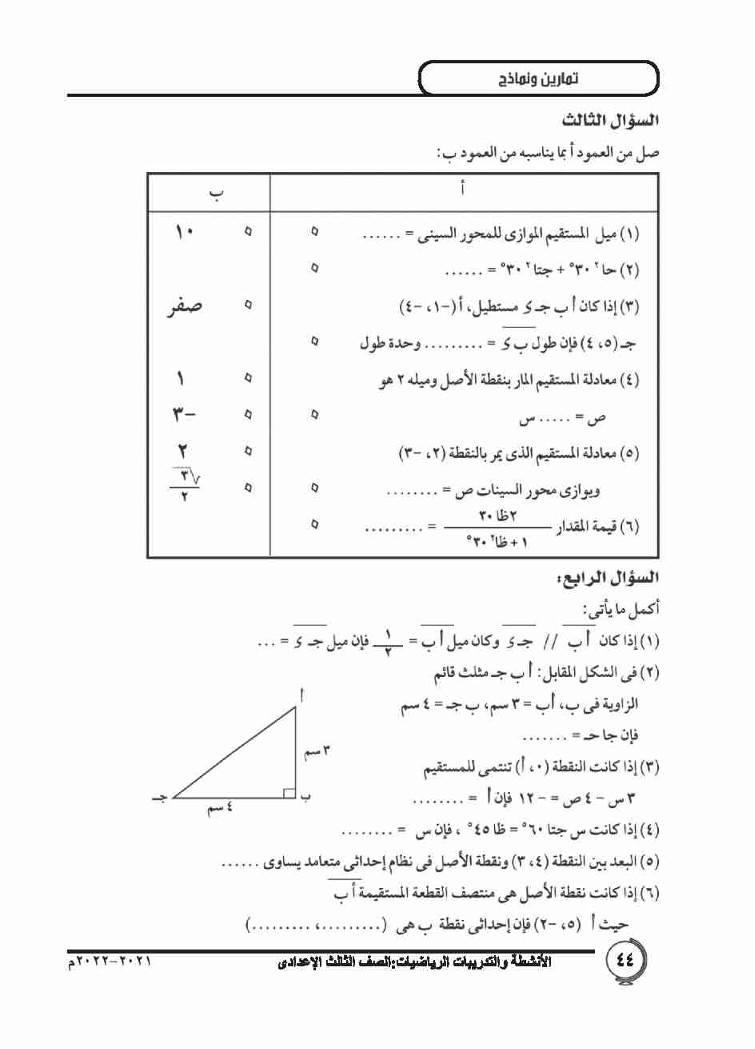
صل من العمود أ بما يناسبه من العمود ب
أكمل ما يأتي






