رياضيات 1
الوحدة الرابعة: متوسطات المثلث والمثلث المتساوي الساقين
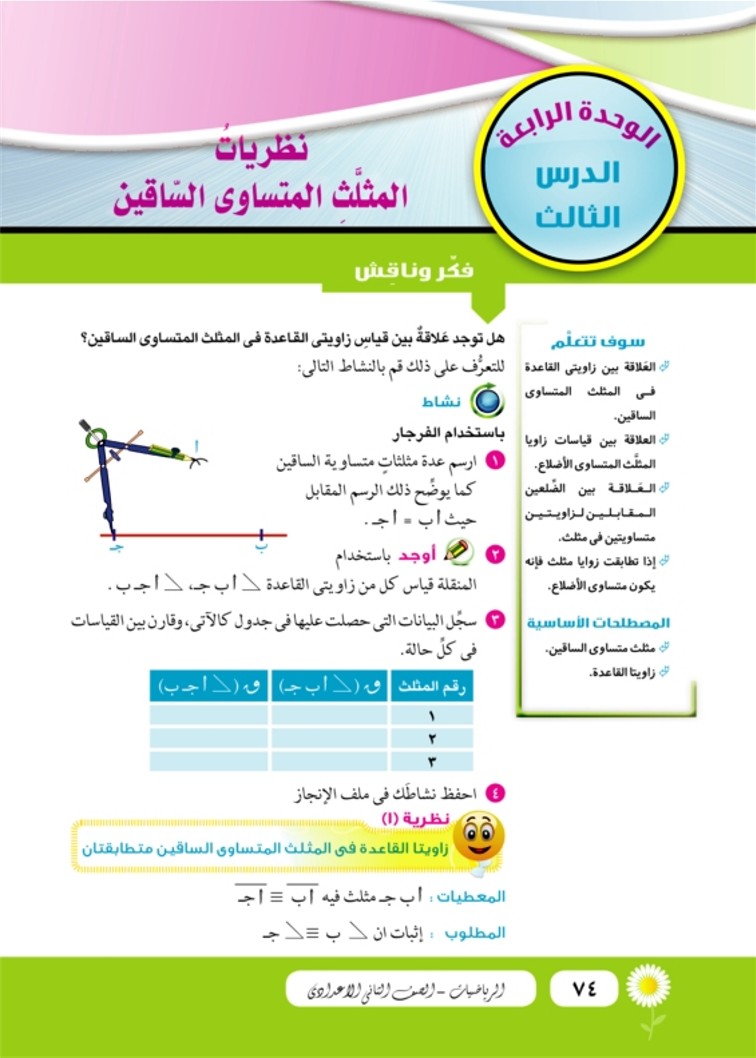
الدرس الثالث: نظريات المثلث المتساوي الساقين
نظريات المثلث المتساوي الساقين - رياضيات 1 - ثاني اعدادي
الوحدة الأولى: الأعداد الحقيقية
الوحدة الثانية: العلاقة بين متغيرين
الوحدة الثالثة: الإحصاء
الوحدة الرابعة: متوسطات المثلث والمثلث المتساوي الساقين
الوحدة الخامسة: التباين
كتاب النشاط
الأنشطة والتدريبات
الوحدة الأولى: الأعداد الحقيقية
الوحدة الثانية: العلاقة بين متغيرين
الوحدة الثالثة: الإحصاء
الوحدة الرابعة: متوسطات المثلث والمثلث المتساوي الساقين
ناصر سالم
- عادل 00:41
02:04
(1)
5
فكر وناقش هل توجد علاقة بين قياس زاويتي القاعدة في المثلث المتساوي الساقين؟
تابع نظرية1
تدرب : في كل من الأشكال الآتية أوجد قيمة الرمز المستخدم في قياس الزاوية
تابع تدرب: في الشكل المقابل أ ب ج مثلث متساوي الساقين فيه أ ب = أ ج أوجد ما يأتي
نتيجة إذا كان المثلث متساوي الأضلاع فإن زواياه الثلاثة تكون متطابقة ويكون قياس كل منها 60 °
مثال1: في الشكل المقابل : أ ب ج مثلث متساوي الأضلاع د تنتمي ب ج بحيث ب ج = ج د اثبت أن ب أ عمودي على أ د
مثال في الشكل المقابل أ ب = أ د , ب ي = ج د , أثبت أن الزاوية أ ب ج = الزاوية أ د ج
تدرب في كل من الأشكال الآتية أوجد قيمة الرمز المستخدم لقياس الزاوية
نظرية ( 2 ) إذا تطابقت زاويتان في مثلث فإن الضلعين المقابلين لهاتين الزاويتين يكونان متطابقين ، ويكون المثلث متساوي الساقين
نتيجة اذا تطابقت زوايا مثلث فإنه يكون متساوي الأضلاع
تدرب : في كل من الأشكال الآتية اكتب أضلاع المثلث المتساوية في الطول كما في المثال
تابع تدرب
أمثلة : في الشكل المقابل أ ب ج مثلث فيه = أ ج , س ص يوازي ب ج أثبت أن المثلث أ س ص متساوي الساقين
في الشكل المقابل أ ب ج مثلث قائم الزاوية في ب , ق الزاوية ج = 30, د تنتمي إلى أ ج بحيث د ب = د ج اثبت أن المثلث أ ب د متساوي الأضلاع
لم يتم إضافة أي تعليقات حتى الآن.
الرجاء تسجيل الدخول لكتابة تعليق
